Гидравлическое сопротивление: виды и коэффициенты
Местные гидравлические сопротивления — зачастую причина кавитации. Как рассчитывать коэффициенты разных сопротивлений? Какова зависимость между сопротивлениями и кавитацией?
Оглавление:
Коэффициент гидравлического сопротивления;
Местные гидравлические сопротивления;
Одно из основных понятий в гидравлике — гидравлические потери (сопротивление). Речь идет о потерях, которые наблюдаются при движении жидкости по водопроводящим каналам.
Условно гидравлические потери можно разделить на две группы:
- потери трения. Представляют собой следствие движения жидкости в проточной части насоса, каналах или трубах;
- потери на вихреобразовании. Обусловлены обтеканием потоком жидкости разнообразных деталей, конструкций, препятствий.
 Это может быть клапан, поворот или сужение трубы. Потери этого типа обычно называют местными гидравлическими сопротивлениями.
Это может быть клапан, поворот или сужение трубы. Потери этого типа обычно называют местными гидравлическими сопротивлениями.
Исследования потерь энергии потока (потерь напора насосов), обусловленных местными сопротивлениями, проводятся уже не одно десятилетие. В разное время в России и за рубежом проводились различные экспериментальные исследования, которые позволили получить множество данных относительно разных местных сопротивлений. В теории гидравлических сопротивлений ученые продвинулись не так далеко: до сих пор не удается создать универсальные формулы, которые можно было бы применять с любыми типами локальных сопротивлений, — пока речь идет о некоторых местных сопротивлениях.
Коэффициент гидравлического сопротивления: это что такое и как высчитывается
Гидравлическое сопротивление измеряется в единицах давления или линейных единицах столба жидкости, потерях напора.
Общая формула потери напора выглядит так:
△H = △P/(pg),
где △P — потери в единицах давления,
p — плотность среды,
g — ускорение свободного падения.
В сфере промышленности, в производственной практике перемещение жидкостей в потоках неразрывно связано с необходимостью преодоления гидравлического сопротивления трубы по всему пути потока. Кроме этого, гидравлические потери обуславливаются местным сопротивлением встречающихся на пути ответвлений и кранов, задвижек и вентилей, поворотов и диафрагм.
Чтобы преодолевать местные сопротивления, поток затрачивает определенную часть энергии — в этом случае речь идет о потере напора на локальные сопротивления. Как правило, такие потери выражают в долях от скоростного напора, который соответствует средней скорости среды в трубах до местного сопротивления либо после него.
Найти данные о коэффициентах местных гидравлических сопротивлений можно в соответствующих учебниках, пособиях, справочниках по гидравлике — данные могут быть представлены в разном виде, например как отдельные значения коэффициента гидравлических потерь, в виде диаграмм, таблиц, эмпирических формул.
При желании или необходимости потери напора на локальные гидравлические сопротивления можно рассчитать самостоятельно. Для этого используется формула:
hr = ξ υ² / (2g),
где ξ представляет собой коэффициент местного сопротивления. Как правило, его определяют опытным путем,
g — ускорение свободного падения.
Местные гидравлические сопротивления: свойства и характеристики
Как мы уже упоминали, потери напора жидкости в случае с местными сопротивлениями определяются в большинстве случаев только опытным путем. Но и в теоретическом обосновании есть некоторые прорывы — так, местное сопротивление по своим свойствам и характеристикам аналогично сопротивлению, которое наблюдается при внезапном расширении струи. И это логично, если учитывать, что поведение потока жидкости при преодолении любого локального сопротивления сопровождается сужением или расширением сечения.
Виды местных сопротивлений:
1. При внезапном сужении трубы сопротивление сопровождается появлением водоворотной области в месте сужения, при этом струя уменьшается до размеров меньших, чем сечение наименьшей трубы. После того как поток проходит участок сужения, струя максимально расширяется, ограничиваясь внутренним сечением трубы. Коэффициент местного сопротивления при резком сужении трубы рассчитывается по формуле: ξвн.суж. = 0,5(1 — (F2/F1)). Значение коэффициента от отношения F2/F1 несложно найти в соответствующих пособиях по гидравлике.
2. При изменении направления трубы под углом гидравлические потери рассчитываются по формуле: ξ поворот = 0,946sin(α/2) + 2,047sin(α/2)², где α — это угол поворота трубы. Поток ведет себя следующим образом: сначала струя сжимается, после чего расширяется, так как при повороте по инерции поток отжимается от стенок трубы.
3. При входе в трубу цилиндрической формы с острой кромкой, которая наклонена к горизонту под углом α, коэффициент местного сопротивления высчитывается по формуле Вейсбаха: ξвх = 0,505 + 0,303sin α + 0,223sin α². Иногда труба имеет закругленную форму или в сечении входа стоит диафрагма, которая сужает сечение, — в любом случае сначала струя потока будет сжиматься, потом расширяться, то есть местное сопротивление при входе в водопровод можно свести к внезапному расширению струи потока.
Иногда труба имеет закругленную форму или в сечении входа стоит диафрагма, которая сужает сечение, — в любом случае сначала струя потока будет сжиматься, потом расширяться, то есть местное сопротивление при входе в водопровод можно свести к внезапному расширению струи потока.
4. В промышленности, в частности при работе с насосным оборудованием, часто приходится рассчитывать местные сопротивления, которые создаются запорной арматурой — вентилями и клапанами, кранами и задвижками и так далее. Вне зависимости от того, какую геометрическую форму имеет проточная часть, ограниченная запорной арматурой, гидравлический характер течения при преодолении сопротивлений не меняется. Если мы говорим о полностью открытой запорной арматуре, гидравлическое сопротивление будет колебаться в диапазоне от 2,9 до 4,5. Коэффициенты для определенного вида запорной арматуры можно найти в соответствующих справочниках.
5. Гидравлические потери диафрагмы определяются сужением струи потока и последующим ее расширением.
6. Наконец, часто бывает необходимо рассчитать коэффициент местного сопротивления при входе струи потока под уровень жидкости. Впрочем, сложных расчетов проводить не потребуется, коэффициент сопротивления при входе струи в большой резервуар под уровень жидкости или в среду без жидкости связан с потерей кинетической энергии и равен 1.
О гидравлическом сопротивлении, насосах и кавитации
Работа насосов и гидравлических машин направлена в том числе на преодоление гидравлических потерь. Чтобы снизить влияние таких потерь, при создании трассы стоит избегать узлов, которые будут резко менять направления потока. Оптимальный вариант — конструкции обтекаемой формы. Но нужно понимать, что даже максимально гладкие трубы не обеспечат отсутствие потерь: ламинарный режим течения не сопровождается большими потерями из-за шероховатых стенок, но турбулентный режим приводит и к росту гидравлического сопротивления трубы.
Иногда при движении жидкости по закрытым руслам меняется ее агрегатное состояние — она превращается в пар, то есть из жидкости выделяются газы, в ней растворенные. Если скорость небольшая, видимых изменений в ее движении не будет. Но при увеличении скорости движения на узком участке трубы появится отчетливая зона с пузырьками газа. Далее, когда жидкость подходит к широкой части трубы, пузырьки начинают резко уменьшаться в размерах, а затем исчезать — схлопываться. В месте схлопывания пузырьков резко увеличивается давление, которое затем передается на соседние объемы среды и далее на стенки трубы. Многочисленные местные повышения давлений приводят к вибрации.
Кавитация — нежелательное явление, которое может привести к очень быстрому износу определенных частей трубопроводного и насосного оборудования. Часто она возникает в местах локальных сопротивлений — в вентилях, кранах, задвижках и так далее. При этом кавитация снижает КПД, а в долгосрочной перспективе разрушает детали, стенки трубопроводов, уменьшая их пропускную способность.
#ФОРМА#
Гидравлические сопротивления
Потери энергии (уменьшение гидравлического напора) можно наблюдать в движущейся жидкости не только на сравнительно длинных участках, но и на коротких. В одних случаях потери напора распределяются (иногда равномерно) по длине трубопровода — это линейные потери; в других — они сосредоточены на очень коротких участках, длиной которых можно пренебречь, — на так называемых местных гидравлических сопротивлениях: вентили, всевозможные закругления, сужения, расширения и т.д., короче всюду, где поток претерпевает деформацию. Источником потерь во всех случаях является вязкость жидкости.
Следует заметить, что потери напора и по длине и в местных гидравлических сопротивлениях существенным образом зависят от так называемого режима движения жидкости.
Третья область — область больших Re и Δ/r0, где коэффициент λ
не зависит от числа Re, а определяется лишь относительной шероховатостью (область расположена справа от
пунктирной линии). Это область шероховатых труб, в которой все линии с различными шероховатостями
параллельны между собой. Эту область называют областью автомодельности или режимом квадратичного
сопротивления, т.к. здесь гидравлические потери пропорциональны квадрату скорости.
Это область шероховатых труб, в которой все линии с различными шероховатостями
параллельны между собой. Эту область называют областью автомодельности или режимом квадратичного
сопротивления, т.к. здесь гидравлические потери пропорциональны квадрату скорости.
Итак, потери напора, определяемые по формуле Вейсбаха-Дарси, можно определить, зная коэффициент
гидравлического сопротивления, который определяется в зависимости от числа Рейнольдса Re и от эквивалентной
абсолютной шероховатости Δ
Пользоваться приведенными в табл. 4.1 формулами для определения коэффициента λ не всегда удобно. Для облегчения расчетов можно воспользоваться номограммой Колбрука-Уайта (рис.4.8), при помощи которой по известным Re и Δэ/ d весьма просто определяется λ.
Рис. 4.8. Номограмма Колбрука-Уайта для определения коэффициента гидравлического трения
4.5. Местные гидравлические сопротивления
Все гидравлические потери энергии делятся на два типа: потери на трение по длине трубопроводов (рассмотрены
в п. 4.3 и 4.4) и местные потери, вызванные такими элементами трубопроводов, в которых вследствие изменения
размеров или конфигурации русла происходит изменение скорости потока, отрыв потока от стенок русла и
возникновение вихреобразования.
4.3 и 4.4) и местные потери, вызванные такими элементами трубопроводов, в которых вследствие изменения
размеров или конфигурации русла происходит изменение скорости потока, отрыв потока от стенок русла и
возникновение вихреобразования.
Простейшие местные гидравлические сопротивления можно разделить на расширения, сужения и повороты русла, каждое из которых может быть внезапным или постепенным. Более сложные случаи местного сопротивления представляют собой соединения или комбинации перечисленных простейших сопротивлений.
Рассмотрим простейшие местные сопротивления при турбулентном режиме течения в трубе.
1. Внезапное расширение русла. Потеря напора (энергии) при внезапном расширении русла расходуется на вихреобразование, связанное с отрывом потока от стенок, т.е. на поддержание вращательного непрерывного движения жидких масс с постоянным их обновлением.
Рис. 4.9. Внезапное расширение трубы
При внезапном расширении русла (трубы) (рис.4.9) поток срывается с угла и расширяется не внезапно, как
русло, а постепенно, причем в кольцевом пространстве между потоком и стенкой трубы образуются вихри, которые
и являются причиной потерь энергии. Рассмотрим два сечения потока: 1-1 — в плоскости расширения трубы и 2-2 — в том месте, где поток, расширившись, заполнил все сечение широкой трубы. Так как поток между
рассматриваемыми сечениями расширяется, то скорость его уменьшается, а давление возрастает. Поэтому второй
пьезометр показывает высоту на ΔH большую, чем первый; но если бы потерь напора в
данном месте не было, то второй пьезометр показал бы высоту большую еще на hрасш. Эта
высота и есть местная потеря напора на расширение, которая определяется по формуле:
Рассмотрим два сечения потока: 1-1 — в плоскости расширения трубы и 2-2 — в том месте, где поток, расширившись, заполнил все сечение широкой трубы. Так как поток между
рассматриваемыми сечениями расширяется, то скорость его уменьшается, а давление возрастает. Поэтому второй
пьезометр показывает высоту на ΔH большую, чем первый; но если бы потерь напора в
данном месте не было, то второй пьезометр показал бы высоту большую еще на hрасш. Эта
высота и есть местная потеря напора на расширение, которая определяется по формуле:
где S1, S2 — площадь поперечных сечений 1-1 и 2-2.
Это выражение является следствием теоремы Борда, которая гласит, что потеря напора при внезапном расширении русла равна скоростному напору, определенному по разности скоростей
Выражение ( 1 — S1/S2 )2 обозначается греческой буквой ζ (дзета) и называется коэффициентом потерь, таким образом2. Постепенное расширение русла. Постепенно расширяющаяся труба называется диффузором (рис.4.10).
Течение скорости в диффузоре сопровождается ее уменьшением и увеличением давления, а следовательно,
преобразованием кинетической энергии жидкости в энергию давления. В диффузоре, так же как и при внезапном
расширении русла, происходит отрыв основного потока от стенки и вихреобразования. Интенсивность этих явлений
возрастает с увеличением угла расширения диффузора α.
Постепенное расширение русла. Постепенно расширяющаяся труба называется диффузором (рис.4.10).
Течение скорости в диффузоре сопровождается ее уменьшением и увеличением давления, а следовательно,
преобразованием кинетической энергии жидкости в энергию давления. В диффузоре, так же как и при внезапном
расширении русла, происходит отрыв основного потока от стенки и вихреобразования. Интенсивность этих явлений
возрастает с увеличением угла расширения диффузора α.
Рис. 4.10. Постепенное расширение трубы
Кроме того, в диффузоре имеются и обычные потери на терние, подобные тем, которые возникают в трубах постоянного сечения. Полную потерю напора в диффузоре рассматривают как сумму двух слагаемых:
где hтр и hрасш — потери напора на трение и расширение (вихреобразование). где n = S2/S1 = ( r2/r1 ) 2 — степень расширения диффузора. Потеря напора на расширение hрасш имеет ту же самую природу, что и при внезапном расширении руслагде k — коэффициент смягчения, при α= 5…20°, k = sinα.
Учитывая это полную потерю напора можно переписать в виде:
откуда коэффициент сопротивления диффузора можно выразить формулой
Рис. 4.11. Зависимость ζдиф от угла
Функция ζ = f(α)имеет минимум при некотором наивыгоднейшем оптимальном значении угла α, оптимальное значение которого определится следующим выражением:
При подстановке в эту формулу λТ =0,015…0,025 и n = 2…4 получим αопт = 6 (рис.4.11).
3. Внезапное сужение русла. В этом случае потеря напора обусловлена трением потока при входе в более узкую трубу и потерями на вихреобразование, которые образуются в кольцевом пространстве вокруг суженой части потока (рис.4.12).
где коэффициент сопротивления сужения определяется по полуэмпирической формуле И.Е. Идельчика:
При выходе трубы из резервуара больших размеров, когда можно считать, что S2/S1 = 0, а также при
отсутствии закругления входного угла, коэффициент сопротивления ζсуж = 0,5.
4. Постепенное сужение русла. Данное местное сопротивление представляет собой коническую сходящуюся трубу, которая называется конфузором (рис.4.13). Течение жидкости в конфузоре сопровождается увеличением скорости и падением давления. В конфузоре имеются лишь потери на трение
Небольшое вихреобразование и отрыв потока от стенки с одновременным сжатием потока возникает лишь на выходе из конфузора в месте соединения конической трубы с цилиндрической. Закруглением входного угла можно значительно уменьшить потерю напора при входе в трубу. Конфузор с плавно сопряженными цилиндрическими и коническими частями называется соплом (рис.4.14).
5. Внезапный поворот трубы (колено). Данный вид местного сопротивления (рис.4.15) вызывает значительные потери энергии, т.к. в нем происходят отрыв потока и вихреобразования, причем потери тем больше, чем больше угол δ. Потерю напора рассчитывают по формуле
где ζкол — коэффициент сопротивления колена круглого сечения, который определяется по
графику в зависимости от угла колена δ (рис. 4.16).
4.16).
6. Постепенный поворот трубы (закругленное колено или отвод). Плавность поворота значительно уменьшает интенсивность вихреобразования, а следовательно, и сопротивление отвода по сравнению с коленом. Это уменьшение тем больше, чем больше относительный радиус кривизны отвода R / d рис.4.17). Коэффициент сопротивления отвода ζотв зависит от отношения R / d, угла δ, а также формы поперечного сечения трубы.
Для отводов круглого сечения с углом δ= 90 и R/d 1 при турбулентном течении можно воспользоваться эмпирической формулой:
Все выше изложенное относится к турбулентному движению жидкости. При ламинарном движении местные сопротивления играют малую роль при определении общего сопротивления трубопровода. Кроме этого закон сопротивления при ламинарном режиме является более сложным и исследован в меньшей степени.
Гидравлическое сопротивление
Существует два типа гидравлического сопротивления: сопротивление трению и местное сопротивление. В первом случае гидравлическое сопротивление связано с передачей импульса твердым стенкам. В последнем случае сопротивление обусловлено диссипацией механической энергии при резком изменении конфигурации или направления потока, образованием вихрей и вторичных течений в результате срыва потока, действием центробежных сил и т. д. К категории местных сопротивлений обычно относят сопротивления переходников, патрубков, удлинителей, диафрагм, арматуры трубопроводов, поворотных колен, вводов в трубы и т. д.
В первом случае гидравлическое сопротивление связано с передачей импульса твердым стенкам. В последнем случае сопротивление обусловлено диссипацией механической энергии при резком изменении конфигурации или направления потока, образованием вихрей и вторичных течений в результате срыва потока, действием центробежных сил и т. д. К категории местных сопротивлений обычно относят сопротивления переходников, патрубков, удлинителей, диафрагм, арматуры трубопроводов, поворотных колен, вводов в трубы и т. д.
При определении полного сопротивления (потери давления Δp f ) используется условная суперпозиция
Сопротивление трению (перепад давления по длине каналов) рассчитывается по эмпирической формуле Дарси
где — коэффициент трения Муди (в 4 раза больше коэффициента трения Фаннинга — см. «Коэффициент трения»), 1 и D H = 4S/P — длина и гидравлический диаметр канала, ρ — плотность жидкости, а u — средняя скорость потока.
Для определения местного гидравлического сопротивления (ΔP 1 ) используется формула Вейсбаха
где ζ — коэффициент местного сопротивления.
Для течения в гладких каналах коэффициент трения f зависит от условий течения и зависит только от Re = ūD H /ν. Для ламинарного течения значение для прямых труб определяется по формуле Пуазейля:
Значения C зависят от формы сечения и приведены в таблице 1.
Мы можем видеть из уравнения. (2) что в ламинарном потоке перепад давления зависит от средней скорости движения в первой степени: линейный закон сопротивления (область I, рис. 1). В турбулентном течении сопротивление гидравлическому трению резко возрастает (участок II). Такой рост сопротивления обусловлен большими потерями энергии, связанными с пульсирующим движением турбулентных вихрей в потоке жидкости. Величина при турбулентном течении в круглой трубе может быть рассчитана по формуле Блазиуса для 5 × 10 3 ≤ Re ≤ 10 5
и из формулы Никурадзе для 10 5 ≤ Re ≤ 4 × 10 6
Приведенные формулы справедливы для течения в каналах с гладкими стенками при полностью сложившихся гидравлических и тепловых условиях. Во входной зоне канала (длиной до 20D H ) имеет более высокое значение, чем рассчитанное по формулам. (5) и (6). На коэффициент трения влияют изменения физических свойств жидкости, вызванные колебаниями температуры и действием сил плавучести.
Во входной зоне канала (длиной до 20D H ) имеет более высокое значение, чем рассчитанное по формулам. (5) и (6). На коэффициент трения влияют изменения физических свойств жидкости, вызванные колебаниями температуры и действием сил плавучести.
В шероховатых каналах увеличивается гидравлическое сопротивление за счет образования вихрей на элементах шероховатости, что приводит к дополнительным потерям удельной энергии потока. Можно выделить три типа шероховатости:
Естественная шероховатость, которая образуется в результате длительной эксплуатации трубопроводов.
Песчаная шероховатость, характеризующаяся высокой плотностью и различной формой конкреций.
Искусственная (или регулярная) шероховатость, когда элементы шероховатости имеют определенную геометрическую форму и расположение.
Каждый тип шероховатости имеет свою специфику изменения коэффициента сопротивления трения с Re. В случае песчаной шероховатости за параметр шероховатости принимается отношение радиуса трубы r 0 к средней высоте выступа δ r на поверхности стенки (k = r 0 /δ r ). До определенного значения Re сопротивление шероховатой трубы изменяется так же, как и гладкой (рис. 2) (при ламинарном течении изменяется по уравнению (4) (кривая 1), при турбулентном течении — по уравнению (5) (кривая 2). Это связано с тем, что вначале толщина ламинарного подслоя у стенки δlam превышает среднюю высоту выступов шероховатости. (δ лам > δ r ). При дальнейшем увеличении Re δ r становится больше, чем δ lam . Это приводит к увеличению сопротивления трения шероховатой трубы по сравнению с гладкой выше некоторого числа перехода Re tr , величина которого зависит от параметра шероховатости: Re tr 100k. При Re > Re tr (автомодельное течение) наблюдается квадратичный закон сопротивления, когда коэффициент сопротивления трению зависит только от значения параметра k (кривая 3 на рис.
В случае песчаной шероховатости за параметр шероховатости принимается отношение радиуса трубы r 0 к средней высоте выступа δ r на поверхности стенки (k = r 0 /δ r ). До определенного значения Re сопротивление шероховатой трубы изменяется так же, как и гладкой (рис. 2) (при ламинарном течении изменяется по уравнению (4) (кривая 1), при турбулентном течении — по уравнению (5) (кривая 2). Это связано с тем, что вначале толщина ламинарного подслоя у стенки δlam превышает среднюю высоту выступов шероховатости. (δ лам > δ r ). При дальнейшем увеличении Re δ r становится больше, чем δ lam . Это приводит к увеличению сопротивления трения шероховатой трубы по сравнению с гладкой выше некоторого числа перехода Re tr , величина которого зависит от параметра шероховатости: Re tr 100k. При Re > Re tr (автомодельное течение) наблюдается квадратичный закон сопротивления, когда коэффициент сопротивления трению зависит только от значения параметра k (кривая 3 на рис. 2): . Значение для труб с коммерческой шероховатостью можно оценить по формуле Коулбрука-Уайта
2): . Значение для труб с коммерческой шероховатостью можно оценить по формуле Коулбрука-Уайта
Здесь k s — эквивалентная шероховатость песка, которая для новых труб из черных металлов составляет около 0,01 мм, а для новых стальных труб — около 0,014 мм; после нескольких лет эксплуатации он увеличивается примерно до 0,2 мм. Для старых ржавых труб k s 1 – 3 мм и для новых оцинкованных труб 0,5 мм; для новых асбестоцементных труб – 0,085 мм.
Таблица 1. Коэффициент, связывающий коэффициент трения и Re −1 в уравнении. (4)
Рисунок 1. Изменения давления ионов в зависимости от средней скорости.
Рисунок 2. Изменение коэффициента трения в зависимости от числа Рейнольдса.
Для искусственной шероховатости из-за ее разнообразия не существует уникальных обобщающих параметров шероховатости. В таком случае для определения гидравлического сопротивления могут быть использованы специальные методики расчета. Значения для типовой арматуры и др. приведены в книге Идельчика (1992).
Значения для типовой арматуры и др. приведены в книге Идельчика (1992).
В плавных изгибах и в змеевиках с R/r 0 ≥ 3 принимаем, что ΔP 1 = 0, а влияние центробежных сил учтено путем подстановки эффективного значения коэффициента сопротивления трения в уравнение (2): для ламинарного потока
для турбулентного течения (Re > 10 4 )
где – коэффициент сопротивления трению для прямой трубы; D = 1/2 Re — число Дина, r 0 — радиус трубы, R — радиус кривизны.
ЛИТЕРАТУРА
Идельчик И, (1992) Справочник гидравлического сопротивления (2-е изд.) Begell House, Нью-Йорк.
Schlichting, H. (1979) Теория пограничного слоя , McGraw Hill, New York.
Теплообменник, Справочник по проектированию (1983), том. 1 и 2, издательская корпорация Hemisphere.
Каталожные номера
- Идельчик, И, (1992) Справочник по гидравлическому сопротивлению (2-е изд.
 ) Begell House, Нью-Йорк.
) Begell House, Нью-Йорк. - Шлихтинг, Х. (1979) Теория пограничного слоя , МакГроу Хилл, Нью-Йорк.
- Теплообменник, Справочник по проектированию (1983 г.), том. 1 и 2, издательская корпорация Hemisphere.
Гидравлическое сопротивление — Learnchannel-TV.com
Гидравлическое сопротивление — потери давления на компонентахВ чем разница между ламинарным и турбулентным потоком:
Определить гидравлическое сопротивление
Одной из проблем гидравлики является перепад давления в трубах и компонентах гидравлического контура. Каждая линия, каждый компонент противодействует объемному потоку, как только проходят потоки масла. Отношение перепада давления к объемному расходу определяется как (гидравлическое) сопротивление. Величина этого сопротивления сильно зависит от типа течения в трубе (ламинарного или турбулентного). Чтобы иметь возможность определить гидравлическое сопротивление и, следовательно, потерю давления, мы должны сначала более внимательно изучить условия потока:
В чем разница между ламинарным и турбулентным потоком:
Различие между ламинарным и турбулентным потоком
Ламинарный поток возникает, когда скорость потока масла можно считать низкой. Здесь масло движется быстрее всего в центре трубы. На стенке трубы масло наиболее тормозится. Между ними отдельные слои масла скользят друг по другу. Это приводит к параболическому профилю скорости внутри трубы.
Здесь масло движется быстрее всего в центре трубы. На стенке трубы масло наиболее тормозится. Между ними отдельные слои масла скользят друг по другу. Это приводит к параболическому профилю скорости внутри трубы.
Турбулентный поток возникает при увеличении объемного расхода. При высоких расходах эти завихрения могут увеличиваться настолько, что течение становится полностью хаотичным.
Чтобы определить, когда поток жидкости превращается из ламинарного в турбулентный, можно применить так называемое число Рейнольдса (названное в честь физика Осборна Рейнольдса). Число Рейнольдса учитывает плотность жидкости, скорость потока, вязкость и геометрию потока (например, диаметр трубы).
Иллюстрация потока масла в сужающемся поперечном сечении трубы
Если предположить, что трубы и шланги имеют круглые и гладкие внутренние поверхности, гидравлическая система принимает следующие значения числа Рейнольдса: Re критический около 2200 . .. 2300 и
.. 2300 и
Re
Re> Re крит 9016 8 => поток турбулентный
Определить гидравлическое сопротивление
Гидравлическое сопротивление — это сопротивление потоку, возникающее в результате объемного потока через гидравлические компоненты (например, трубы, клапаны и т. д.).
Падение давления из-за гидравлического сопротивления
Определить гидравлическое сопротивление
В случае ламинарного потока перепад давления Δp пропорционален объемному расходу Q на определенной длине трубы. Таким образом, гидравлическое сопротивление R можно легко определить:
R = Δp /Q Уравнение. 1
В турбулентном потоке перепад давления увеличивается квадратично с увеличением объемного расхода: Δp ~ Q 2
Для простоты течение в трубе считается ламинарным до тех пор, пока турбулентный участок не разрастется настолько, что перевешивает (пересечение обеих кривых).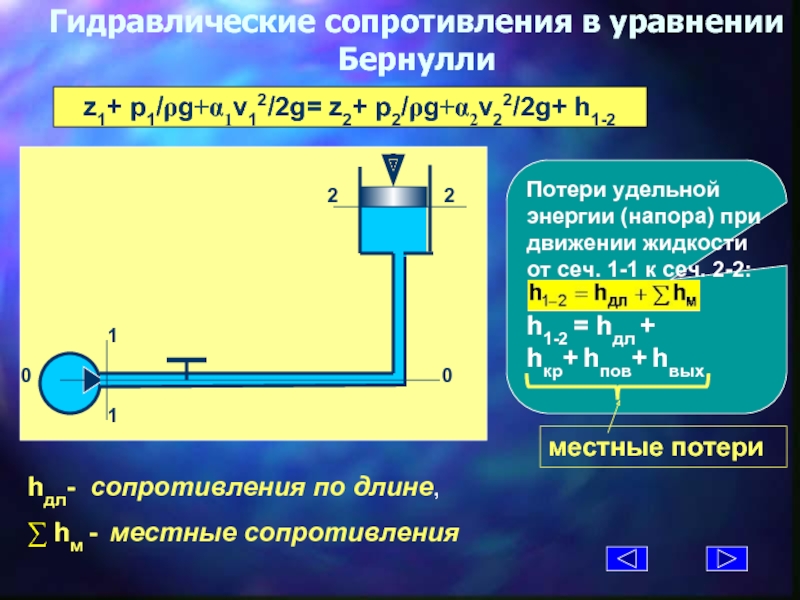

 Это может быть клапан, поворот или сужение трубы. Потери этого типа обычно называют местными гидравлическими сопротивлениями.
Это может быть клапан, поворот или сужение трубы. Потери этого типа обычно называют местными гидравлическими сопротивлениями.