Что такое тепловые процессы: Тепловой процесс — Википедия – Тепловой процесс — это… Что такое Тепловой процесс?

Тепловой процесс — Википедия

Материал из Википедии — свободной энциклопедии

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 14 марта 2013; проверки требуют 10 правок. Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 14 марта 2013; проверки требуют 10 правок.

Тепловой процесс (термодинамический процесс) — изменение макроскопического состояния термодинамической системы. Если разница между начальным и конечным состояниями системы бесконечно мала, то такой процесс называют элементарным (инфинитезимальным)^[1].

Система, в которой идёт тепловой процесс, называется рабочим телом.

Тепловые процессы можно разделить на равновесные и неравновесные. Равновесным называется процесс, при котором все состояния, через которые проходит система, являются равновесными состояниями. Такой процесс приближённо реализуется в тех случаях, когда изменения происходят достаточно медленно, т. е. процесс является

квазистатическим^[1].

Тепловые процессы можно разделить на обратимые и необратимые. Обратимым называется процесс, который можно провести в противоположном направлении через все те же самые промежуточные состояния.

Процессы принято классифицировать по тем термодинамическим величинам, которые остаются неизменными в ходе процесса^[2]. Можно выделить несколько простых, но широко распространённых на практике, тепловых процессов:

Иногда в течение всего процесса неизменными оказываются не одна, а несколько термодинамических величин. Так, например, испарение и конденсация в системе жидкость — пар, когда одновременно постоянны и давление и температура, есть процессы изобарно-изотермические^[2].

В технике важны круговые процессы (циклы), то есть повторяющиеся процессы, например, цикл Карно, цикл Ренкина.

Теория тепловых процессов применяется для проектирования двигателей, холодильных установок, в химической промышленности, в метеорологии.

Тепловой процесс — это… Что такое Тепловой процесс?



Тепловой процесс

        термодинамический процесс, изменение состояния физической системы (рабочего тела (См. Рабочее тело)) в результате теплообмена и совершения работы. Если Т. п. протекает настолько медленно, что в каждый момент рабочее тело будет находиться в равновесии термодинамическом (См. Равновесие термодинамическое), то он является равновесным, в противном случае Т. п. — неравновесный процесс (См. Неравновесные процессы). Если Т. п. можно провести в обратном направлении через ту же последовательность промежуточных состояний, то он называется обратимым процессом (См. Обратимый процесс) (такой Т. п. должен быть равновесным). Все реальные Т. п. — Необратимые процессы, поскольку они осуществляются с конечными скоростями, при конечных разностях температур между источником теплоты и рабочим телом и сопровождаются трением и потерями теплоты в окружающую среду.          Т. п. могут происходить при постоянных давлении (Изобарный процесс) , температуре (Изотермический процесс), объёме (Изохорный процесс). Т. п., протекающий без теплообмена с окружающей средой, называется адиабатным процессом (См. Адиабатный процесс); при обратимом адиабатном процессе Энтропия системы остаётся постоянной, то есть процесс изоэнтропийный. Необратимый адиабатный процесс сопровождается увеличением энтропии. Т. п., при котором остаётся постоянной Энтальпия (теплосодержание) системы, — изоэнтальпийный процесс. Круговые процессы (См. Круговой процесс), при осуществлении которых производятся работа, теплота или холод, в технике называются циклами (см. Карно цикл, Ранкина цикл, Холодильные циклы. Цикл двигателя).

         И. Н. Розенгауз.

        

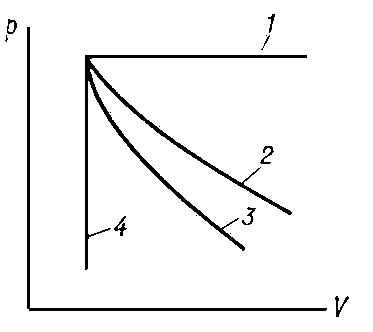
        Графическое изображение тепловых процессов на диаграмме р — V (давление — объём): 1 — изобара; 2 — изотерма; 3 — адиабата; 4 — изохора.

Большая советская энциклопедия. — М.: Советская энциклопедия. 1969—1978.

• Тепловой поток
• Тепловой пункт

Смотреть что такое «Тепловой процесс» в других словарях:

• тепловой процесс — — [А.С.Гольдберг. Англо русский энергетический словарь. 2006 г.] Тематики энергетика в целом EN thermal process …   Справочник технического переводчика

• Тепловой процесс — Тепловые процессы …   Википедия

• тепловой процесс — šiluminis vyksmas statusas T sritis fizika atitikmenys: angl. heat process vok. Wärmevorgang, m rus. тепловой процесс, m pranc. processus thermique, m …   Fizikos terminų žodynas

• тепловой процесс — šiluminis procesas statusas T sritis Energetika apibrėžtis Termodinaminis prosesas, kada termodinaminės būsenos parametrai keičiasi dėl sistemai teikiamos ar atimamos šilumos. atitikmenys: angl. heat process vok. Wärmevorgang, m rus. тепловой… …   Aiškinamasis šiluminės ir branduolinės technikos terminų žodynas

• Процесс — (Process) Определение процесса, виды и типы процессов Информация об определении процесса, виды и типы процессов Содержание Содержание Определение Исторический Бизнес процесс Тепловой процесс Адиабатический процесс Изохорный процесс Изобарный… …   Энциклопедия инвестора

• Тепловой баланс — I Тепловой баланс         сопоставление прихода и расхода (полезно использованной и потерянной) теплоты в различных тепловых процессах (См. Тепловой процесс). В технике Т. б. используется для анализа тепловых процессов, осуществляющихся в паровых …   Большая советская энциклопедия

• Процесс — По теме Процесс должна быть отдельная статья, а не страница разрешения неоднозначностей. После создания основной статьи страницу разрешения неоднозначностей, если в ней будет необходимость, переименуйте в Процесс (значения). Содержание 1… …   Википедия

• Тепловой эффект химической реакции — или изменение энтальпии системы вследствие протекания химической реакции  отнесенное к изменению химической переменной количество теплоты, полученное системой, в которой прошла химическая реакция и продукты реакции приняли температуру… …   Википедия

• Процесс Фишера — Тропша — Процесс Фишера – Тропша  это химическая реакция, происходящая в присутствии катализатора, в которой монооксид углерода (CO) и водород h3 преобразуются в различные жидкие углеводороды. Обычно используются катализаторы, содержащие железо и… …   Википедия

• Процесс Фишера — Тропа — Процесс Фишера  Тропша  это химическая реакция, происходящая в присутствии катализатора, в которой монооксид углерода (CO) и водород h3 преобразуются в различные жидкие углеводороды. Обычно используются катализаторы, содержащие железо и кобальт.… …   Википедия

Книги

• Высококвалифицированная швея, Н. В. Горшкова. Рассмотрены ассортимент и свойства современных материалов для изготовления швейных изделий, особенности их конструирования в зависимости от используемых материалов, декоративной отделки… Подробнее  Купить за 546 руб
• Сушка и увлажнение лубоволокнистых материалов. Учебник, В. А. Суметов. Описаны свойства обрабатывающей среды, характеристика влажных материалов, способы сушки и их сущность, теоретические основы конвективной сушки, тепловой расчет воздушных… Подробнее  Купить за 340 руб
• Готовим в горшочках, Л. А. Калугина. Глиняный горшок — самая древняя кухонная посуда. Поэтому, несмотря на огромный арсенал современной посуды, в обществе снова возник интерес к глиняным горшочкам, т. е. интерес к более… Подробнее  Купить за 294 руб

Другие книги по запросу «Тепловой процесс» >>

Тепловой эффект химической реакции — Википедия

Тепловой эффект химической реакции — изменение внутренней энергии ΔU{\displaystyle \Delta U} или энтальпии ΔH{\displaystyle \Delta H} системы вследствие протекания химической реакции и превращения исходных веществ (реактантов) в продукты реакции в количествах, соответствующих уравнению химической реакции (стехиометрии реакции^[1]) при следующих условиях:

• единственно возможной работой при этом является работа против внешнего давления,
• как исходные вещества, так и продукты реакции имеют одинаковую температуру^[2][3].

Теплота термохимического процесса и тепловой эффект химической реакции[править | править код]

Поясним приведённое выше определение теплового эффекта химической реакции

[K 1]. Для этого запишем фундаментальные уравнения Гиббса для внутренней энергии и энтальпии простой^[10]открытой однородной термодинамической системы^[11][12]:

dU=TdS−PdV+∑i=1kμidni,{\displaystyle dU=TdS-PdV+\sum _{i=1}^{k}\mu _{i}dn_{i},}

(Фундаментальное уравнение Гиббса для внутренней энергии)

dH=TdS+VdP+∑i=1kμidni.{\displaystyle dH=TdS+VdP+\sum _{i=1}^{k}\mu _{i}dn_{i}.}

(Фундаментальное уравнение Гиббса для энтальпии)

Здесь T{\displaystyle T} — абсолютная температура, S{\displaystyle S} — энтропия, P{\displaystyle P} — давление, V{\displaystyle V} — объём, ni{\displaystyle n_{i}} — количество (или масса) i{\displaystyle i}-го составляющего систему вещества, μi{\displaystyle \mu _{i}} — химический потенциал этого вещества (см. Энтропия открытой системы).

Для бесконечно малого^[13]квазистатического изохорного процесса (V=const{\displaystyle V=const})

dU=TdS+∑i=1kμidni;{\displaystyle dU=TdS+\sum _{i=1}^{k}\mu _{i}dn_{i};}

(Изменение внутренней энергии в бесконечно малом квазистатическом изохорном процессе)

для бесконечно малого квазистатического изобарного процесса (P=const{\displaystyle P=const})

dH=TdS+∑i=1kμidni.{\displaystyle dH=TdS+\sum _{i=1}^{k}\mu _{i}dn_{i}.}

(Изменение энтальпии в бесконечно малом квазистатическом изобарном процессе)

Важно понимать, что представление о теплоте химической реакции при сохранении исторически сложившегося названия (восходящего ко временам, когда любое изменение температуры связывали с поглощением или выделением теплоты) уже не имеет прямого отношения к общефизическому понятию количества теплоты. Действительно, при химической реакции в изолированной системе (например, инициируемом электрической искрой взрыве гремучего газа в герметически закрытом термосе) может иметь место изменение температуры (за счёт изменения состава системы), но не происходит ни выделения/поглощения теплоты^[14], ни изменения внутренней энергии системы. Наконец, традиционная трактовка теплоты, основанная на представлении об адиабатической изоляции системы от окружающей среды^[15] (см. Неоднозначность понятий «теплота» и «работа») к открытым системам не применима, и для них теплоту q{\displaystyle q} бесконечно малого квазистатического процесса полагают равной^[16][17]

q≡TdS.{\displaystyle q\equiv TdS.}

(Дефиниция теплоты для любого бесконечно малого квазистатического процесса)

Таким образом, теплота бесконечно малого квазистатического изохорного процесса qV{\displaystyle q_{V}} равна

qV=dU−∑i=1kμidni,{\displaystyle q_{V}=dU-\sum _{i=1}^{k}\mu _{i}dn_{i},}

(Теплота бесконечно малого квазистатического изохорного процесса)

а теплота бесконечно малого квазистатического изобарного процесса qP{\displaystyle q_{P}} равна

qP=dH−∑i=1kμidni.{\displaystyle q_{P}=dH-\sum _{i=1}^{k}\mu _{i}dn_{i}.}

(Теплота бесконечно малого квазистатического изобарного процесса)

Для закрытых систем изменение энергии системы за счёт изменения масс составляющих систему веществ (химическую работу^{[18][19][20][21][22]}, работу перераспределения масс составляющих систему веществ^[23]) ∑iμidni{\displaystyle \sum _{i}\mu _{i}dn_{i}} учитывать не требуется^[24][25], и выражения для теплот ещё более упрощаются:

qV=dU,{\displaystyle q_{V}=dU,}

(Теплота бесконечно малого квазистатического изохорного процесса в простой закрытой системе)

qP=dH.{\displaystyle q_{P}=dH.}

(Теплота бесконечно малого квазистатического изобарного процесса в простой закрытой системе)

Из сказанного ясно, почему в дефиниции теплового эффекта химической реакции фигурируют внутренняя энергия, энтальпия и запрет на любые виды работ в системе, кроме работы расширения/сжатия. Уточним, что в понятии «химическая работа» термин «работа» не имеет отношения к понятию «термодинамическая работа» и использован просто как синоним словосочетания «изменение энергии». Наконец, подчеркнём, что когда речь идёт о тепловом эффекте химической реакции, то, как и во многих других случаях, касающихся термохимии, подразумевается, что речь идёт о закрытой системе и полномасштабное применение мощного, но громоздкого математического аппарата термодинамики систем переменного состава не требуется^[24][25][26].

Энергетический эффект химической реакции всегда рассматривают применительно к конкретному термохимическому уравнению, которое может не иметь отношения к реальному химическому процессу. Термохимическое уравнение лишь показывает, какие наборы начальных и конечных индивидуальных веществ, находящихся в определенных состояниях и количественных соотношениях, исчезают и образуются. В начальном состоянии должны присутствовать только исходные вещества (реактанты), а в конечном — только продукты химической реакции. Единственным условием при записи термохимического уравнения является соблюдение материального и зарядового баланса. Вещества в растворённом или адсорбированном состоянии тоже считаются индивидуальными соединениями; если растворитель или адсорбент не участвует непосредственно в химической реакции и не реагирует с растворённым веществом, то он рассматривается просто как фактор, влияющий на термодинамические свойства рассматриваемого вещества. Наконец, в термохимическом уравнении могут фигурировать частицы, не способные к самостоятельному существованию (электроны, протоны, ионы, радикалы, атомарные простые вещества)^[27].

Энергетический эффект реального процесса с химической реакцией зависит от условий проведения процесса и не может служить стандартной характеристикой конкретной химической реакции^[3]. Химическая же термодинамика нуждается в показателе, связанном с энергетикой химической реакции, но не зависящем от условий её проведения. Покажем, как может быть получен интересующий нас показатель. Для этого рассмотрим следующий мысленный эксперимент. Возьмем чистые индивидуальные исходные вещества в мольных количествах, соответствующих стехиометрическим коэффициентам интересующего нас термохимического уравнения, и находящиеся при определенных температуре и давлении. Если привести эти вещества в контакт, то энтальпия образовавшейся неравновесной системы в начальный момент времени будет равна сумме энтальпий исходных веществ. Теперь рассмотрим конечное состояние изучаемой системы в предположении, что реактанты прореагировали полностью^[28] и продукты реакции находятся при той же температуре и том же давлении, что и реактанты. Энтальпия системы (в общем случае неравновесной) из продуктов химической реакции будет равна сумме энтальпий этих веществ. Поскольку энтальпия — функция состояния, то разность энтальпий ΔH{\displaystyle \Delta H} системы в конце и начале рассмотренного мысленного эксперимента не зависит от условий проведения химической реакции. Эту разность энтальпий и называют изобарным тепловым эффектом (термохимической теплотой) химической реакции, соответствующей определённому термохимическому уравнению^[29][30]. Важно, что реальная осуществимость рассмотренного мысленного эксперимента, гипотетические условия его проведения и неравновесность исходного и конечного состояний термохимической системы не сказываются на дефиниции теплового эффекта химической реакции.

Часто тепловой эффект химической реакции относят к 1 молю одного из продуктов реакции^[31].

Резюмируем сказанное: теплота процесса, связанного с фактическим протеканием химической реакции, и энергетический эффект химической реакции отнюдь не одно и то же, а дефиниция теплового эффекта химической реакции вообще не предполагает действительного осуществления реакции, соответствующей рассматриваемому термохимическому уравнению^[32].

И внутренняя энергия, и энтальпия представляют собой функции состояния, поэтому тепловой эффект химической реакции зависит от природы и состояния исходных веществ и конечных продуктов, но не зависит от пути реакции, то есть от числа и характера промежуточных стадий (закон Гесса)^{[33][34][35][36]}.

Тепловой эффект химической реакции, протекающей при постоянном давлении, и равный изменению энтальпии системы в процессе, соответствующем термохимическому уравнению, называется изобарным тепловым эффектом или энтальпией химической реакции. Тепловой эффект химической реакции, протекающей при постоянном объёме, и равный изменению внутренней энергии системы в процессе, соответствующем термохимическому уравнению, называют изохорным тепловым эффектом^[2].

Для отдельных типов химических реакций вместо общего термина «тепловой эффект химической реакции» используют специальные (сокращённые) термины: теплота образования, теплота сгорания и т. п.^[1]

Дефиниции тепловых эффектов должны быть дополнены указанием на начальные точки отсчёта значений энергии и энтальпии. Для сравнения тепловых эффектов и упрощения термодинамических расчётов все величины тепловых эффектов реакций относят к стандартным условиям (все вещества находятся в стандартных состояниях)^[1]. Если реакцию — реально или гипотетически — проводят при стандартных условиях (T = 298,15 К = 25 °С и P = 1 бар = 100 кПа)^[37], то тепловой эффект называют стандартным тепловым эффектом реакции или стандартной энтальпией реакции ΔHo
r.

Химические реакции, сопровождающиеся повышением температуры, называют экзотермическими, понижением температуры — эндотермическими. В термодинамической системе знаков тепловой эффект экзотермической реакции (ΔU<0{\displaystyle \Delta U<0} или ΔH<0{\displaystyle \Delta H<0}) считают отрицательным, эндотермической (ΔU>0{\displaystyle \Delta U>0} или ΔH>0{\displaystyle \Delta H>0}) — положительным. В устаревшей и не рекомендуемой к употреблению термохимической системе знаков положительным, наоборот, считается тепловой эффект экзотермической реакции, а отрицательным — эндотермической^[38].

Тепловые эффекты химических реакций важны для теоретической химии и необходимы при расчётах равновесных составов смесей, выхода продуктов реакций, удельной тяги топлив реактивных двигателей и для решения многих других прикладных задач^[1].

Изучение тепловых эффектов химических реакций составляет важнейшую задачу термохимии^[3]. Для расчёта стандартных тепловых эффектов химических реакций используют таблицы стандартных теплот образования или сгорания^[38].

Стандартная энтальпия образования (стандартная теплота образования)[править | править код]

Под стандартной теплотой образования понимают тепловой эффект реакции образования одного моля вещества из простых веществ, его составляющих, находящихся в устойчивых стандартных состояниях.

Например, стандартная энтальпия образования 1 моля метана из углерода и водорода равна тепловому эффекту реакции:

С(тв) + 2H₂(г) = CH₄(г) + 74,9 кДж/моль.

Стандартная энтальпия образования обозначается ΔHo
f. Здесь индекс f означает formation (образование), а знак «O» в верхнем индексе указывает, что величина относится к стандартному состоянию вещества: один моль индивидуального химического соединения, взятого в чистом виде при стандартных условиях в том агрегатном состоянии, которое устойчиво в этих условиях (если нет специальной оговорки)^[39]. Иногда для обозначения стандартного состояния используют перечёркнутый символ «O» в верхнем индексе; согласно рекомендациям ИЮПАК по использованию обозначений в физической химии^[40], перечёркнутый и неперечёркнутый символ «O», используемые для обозначения стандартного состояния, одинаково приемлемы. В литературе часто встречается другое обозначение стандартной энтальпии — ΔHo
298,15, где знак «O» указывает на равенство давления одной атмосфере^[41] (или, несколько более точно, на стандартные условия^[42]), а 298,15 — температура. Иногда индекс «O» используют для величин, относящихся к чистому веществу, оговаривая, что обозначать им стандартные термодинамические величины можно только тогда, когда в качестве стандартного состояния выбрано именно чистое вещество^[43]. Стандартным также может быть принято, например, состояние вещества в предельно разбавленном растворе.

Энтальпия образования простых веществ принимается равной нулю, причем нулевое значение энтальпии образования относится к агрегатному состоянию, устойчивому при T = 298,15 K. Например, для иода в кристаллическом состоянии ΔH

^o(I₂, тв) = 0 кДж/моль, а для жидкого иода ΔH^o(I₂, ж) = 22 кДж/моль. Энтальпии образования простых веществ при стандартных условиях являются их основными энергетическими характеристиками.

Тепловой эффект любой реакции находится как разность между суммой теплот образования всех продуктов и суммой теплот образования всех реагентов в данной реакции (следствие закона Гесса):

ΔH^o_{реакции} = ΣΔHo
f (продукты) — ΣΔHo
f (реагенты).

Термохимические эффекты можно включать в химические реакции. Химические уравнения в которых указано количество выделившейся или поглощенной теплоты, называются термохимическими уравнениями. Реакции, сопровождающиеся выделением тепла в окружающую среду имеют отрицательный тепловой эффект и называются экзотермическими. Реакции, сопровождающиеся поглощением тепла имеют положительный тепловой эффект и называются эндотермическими. Тепловой эффект обычно относится к одному молю прореагировавшего исходного вещества, стехиометрический коэффициент которого максимален.

Температурная зависимость теплового эффекта (энтальпии) реакции[править | править код]

Чтобы рассчитать температурную зависимость энтальпии реакции, необходимо знать мольные теплоемкости веществ, участвующих в реакции. Изменение энтальпии реакции при увеличении температуры от Т₁ до Т₂ рассчитывают по закону Кирхгофа (предполагается, что в данном интервале температур мольные теплоемкости не зависят от температуры и нет фазовых превращений):

ΔH(T2)=ΔH(T1)+∫12ΔCp(T1,T2)d(T).{\displaystyle \Delta {H(T_{2})}=\Delta {H(T_{1})}+\int \limits _{1}^{2}{\Delta {C_{p}}(T_{1}{,}T_{2})d(T)}.}

Если в данном интервале температур происходят фазовые превращения, то при расчёте необходимо учесть теплоты соответствующих превращений, а также изменение температурной зависимости теплоемкости веществ, претерпевших такие превращения:

ΔH(T2)=ΔH(T1)+∫1TφΔCp(T1,Tφ)d(T)+∫Tφ2ΔCp(Tφ,T2)d(T),{\displaystyle \Delta {H(T_{2})}=\Delta {H(T_{1})}+\int \limits _{1}^{T_{\varphi }}{\Delta {C_{p}}(T_{1}{,}T_{\varphi })d(T)}+\int \limits _{T_{\varphi }}^{2}{\Delta {C_{p}}(T_{\varphi }{,}T_{2})d(T)},}

где ΔC_p(T₁, T_φ) — изменение теплоемкости в интервале температур от Т₁ до температуры фазового перехода; ΔC_p(T_φ, T₂) — изменение теплоемкости в интервале температур от температуры фазового перехода до конечной температуры, и T_φ — температура фазового перехода.

Стандартная энтальпия сгорания — ΔHо
гор., тепловой эффект реакции сгорания одного моля вещества в кислороде до образования оксидов в высшей степени окисления. Теплота сгорания негорючих веществ принимается равной нулю.

Стандартная энтальпия растворения — ΔHо
раств., тепловой эффект процесса растворения 1 моля вещества в бесконечно большом количестве растворителя. Складывается из теплоты разрушения кристаллической решётки и теплоты гидратации (или теплоты сольватации для неводных растворов), выделяющейся в результате взаимодействия молекул растворителя с молекулами или ионами растворяемого вещества с образованием соединений переменного состава — гидратов (сольватов). Разрушение кристаллической решетки, как правило, эндотермический процесс — ΔH_реш. > 0, а гидратация ионов — экзотермический, ΔH_гидр. < 0. В зависимости от соотношения значений ΔH_реш. и ΔH_гидр. энтальпия растворения может иметь как положительное, так и отрицательное значение. Так растворение кристаллического гидроксида калия сопровождается выделением тепла:

ΔHо
раств.KOH = ΔHо
реш. + ΔHо
гидр.К⁺ + ΔHо
гидр.OH⁻ = −59 кДж/моль.

Под энтальпией гидратации ΔH_гидр. понимается теплота, которая выделяется при переходе 1 моля ионов из вакуума в раствор.

Стандартная энтальпия нейтрализации[править | править код]

Стандартная энтальпия нейтрализации ΔHо
нейтр. — энтальпия реакции взаимодействия сильных кислот и оснований с образованием 1 моля воды при стандартных условиях:

HCl + NaOH = NaCl + H₂O

H⁺ + OH⁻ = H₂O, ΔHо
нейтр. = −55,9 кДж/моль

Стандартная энтальпия нейтрализации для концентрированных растворов сильных электролитов зависит от концентрации ионов, вследствие изменения значения ΔHо
гидратации ионов при разбавлении.

1. ↑ В общем случае, когда не выполняются условия, перечисленные в дефиниции теплового эффекта химической реакции, говорят об энергетическом эффекте химической реакции^[4][5][6][7], который при выполнении упомянутых выше условий сводится к выделению/поглощению системой теплоты, то есть именно к тепловому эффекту. В соответствии со сложившейся в термохимии традицией термины «энергетический эффект химической реакции» и «тепловой эффект химической реакции» до сих пор иногда рассматривают как синонимы^[8][9].

1. ↑ ^{1 2 3 4} БСЭ, 3-е изд., т. 25, 1976, с. 450.
2. ↑ ^{1 2} Термодинамика. Основные понятия. Терминология. Буквенные обозначения величин, 1984, с. 16.
3. ↑ ^{1 2 3} Химическая энциклопедия, т. 4, 1995, с. 522—523.
4. ↑ Александров Н. Е. и др., Основы теории тепловых процессов и машин, ч. 2, 2015, с. 290.
5. ↑ Морачевский А. Г., Фирсова Е. Г., Физическая химия. Термодинамика химических реакций, 2015, с. 21.
6. ↑ Карякин Н. В., Основы химической термодинамики, 2003, с. 17, 63.
7. ↑ Шмидт Э., Введение в техническую термодинамику, 1965, с. 311.
8. ↑ Александров Н. Е. и др., Основы теории тепловых процессов и машин, ч. 2, 2015, с. 174.
9. ↑ Нараев В. Н., Физическая химия, ч. 1, 2007, с. 6.
10. ↑ Состояние простой термодинамической системы (газы и изотропные жидкости в ситуации, когда поверхностными эффектами и наличием внешних силовых полей можно пренебречь) полностью задано её объёмом, давлением в системе и массами составляющих систему веществ.
11. ↑ Кубо Р., Термодинамика, 1970, с. 143.
12. ↑ Мюнстер А., Химическая термодинамика, 1971, с. 103.
13. ↑ Бесконечно малым (элементарным, инфинитезимальным) называют процесс, для которого разница между начальным и конечным состояниями системы бесконечно мала.
14. ↑ Под теплотой здесь подразумевается изменение энергии системы в результате теплопередачи через граничную поверхность (см. Теплота).
15. ↑ Термодинамика. Основные понятия. Терминология. Буквенные обозначения величин, 1984, с. 8.
16. ↑ Базаров И. П., Термодинамика, 2010, с. 114.
17. ↑ Залевски К., Феноменологическая и статистическая термодинамика, 1973, с. 54.
18. ↑ Lebon G. e. a., Understanding Non-equilibrium Thermodynamics, 2008, p. 14.
19. ↑ Жариков В. А., Основы физической геохимии, 2005, с. 31.
20. ↑ Callen H. B., Thermodynamics and an Introduction to Thermostatistics, 1985, p. 36.
21. ↑ Сычёв В. В., Сложные термодинамические системы, 2009, с. 257.
22. ↑ Путилов К. А., Термодинамика, 1971, с. 125.
23. ↑ Тамм М. Е., Третьяков Ю. Д., Физико-химические основы неорганической химии, 2004, с. 11.
24. ↑ ^{1 2} Степановских Е. И. и др., Химическая термодинамика в вопросах и ответах, 2014, с. 87.
25. ↑ ^{1 2} Бурдаков В. П. и др., Термодинамика, ч. 2, 2009, с. 10.
26. ↑ Борщевский А. Я., Физическая химия, т. 1, 2017, с. 127.
27. ↑ Борщевский А. Я., Физическая химия, т. 1, 2017, с. 128.
28. ↑ То, что конечное состояние может оказаться недостижимым в действительности, применительно к данному рассмотрению не имеет значения.
29. ↑ Борщевский А. Я., Физическая химия, т. 1, 2017, с. 130.
30. ↑ Морачевский А. Г., Кохацкая М. С., Прикладная химическая термодинамика, 2008, с. 24.
31. ↑ Никольский Б. П. и др., Физическая химия, 1987, с. 17.
32. ↑ Борщевский А. Я., Физическая химия, т. 1, 2017, с. 131.
33. ↑ Ляшков В. И., Теоретические основы теплотехники, 2015, с. 102.
34. ↑ Морачевский А. Г., Кохацкая М. С., Прикладная химическая термодинамика, 2008, с. 23.
35. ↑ Кнорре Д.Г. и др., Физическая химия, 1990, с. 245.
36. ↑ Никольский Б. П. и др., Физическая химия, 1987, с. 18.
37. ↑ До 1982 года ИЮПАК принимал в качестве стандартного давления 1 атм = 101325 Па; это следует учитывать при использовании данных из литературы, изданной ранее.
38. ↑ ^{1 2} Химический энциклопедический словарь, 1983, с. 563.
39. ↑ Курс физической химии // Под ред. Я. И. Герасимова. М.-Л.: Химия, 1964. — Т. 1. — С. 55.
40. ↑ International Union of Pure and Applied Chemistry (1993). Quantities, Units and Symbols in Physical Chemistry, 2nd edition, Oxford: Blackwell Science. ISBN 0-632-03583-8. p. 49. Electronic version.
41. ↑ Жуховицкий А. А., Шварцман Л. А. Физическая химия. — М.: Металлургия, 1976. — 544 с.
42. ↑ Стромберг А. Г., Семченко Д. П. Физическая химия: Учеб. для хим.-технол. спец. вузов / Под ред. А. Г. Стромберга. — 2-е изд. — М.: Высш. шк., 1988. — 496 с.
43. ↑ Пригожин И., Дефэй Р. Химическая термодинамика = Chemical Thermodynamics / Перевод с англ. под ред. В. А. Михайлова. — Новосибирск: Наука, 1966. — 502 с.

• Callen H. B. Thermodynamics and an Introduction to Thermostatistics. — 2nd ed. — N. Y. e. a.: John Wiley, 1985. — XVI + 493 p. — ISBN 0471862568, 9780471862567.
• Lebon G., Jou D., Casas-Vázquez J. Understanding Non-equilibrium Thermodynamics: Foundations, Applications, Frontiers. — Berlin — Heidelberg: Springer, 2008. — XIII + 325 p. — ISBN 978-3-540-74251-7, 978-3-540-74252-4. — doi:10.1007/978-3-540-74252-4.
• Александров Н. Е., Богданов А. И., Костин К. И. и др. Основы теории тепловых процессов и машин. Часть II / Под ред. Н. И. Прокопенко. — 5-е изд. (электронное). — М.: Бином. Лаборатория знаний, 2015. — 572 с. — ISBN 978-5-9963-2613-6. (недоступная ссылка)
• Базаров И. П. Термодинамика. — 5-е изд. — СПб.—М.—Краснодар: Лань, 2010. — 384 с. — (Учебники для вузов. Специальная литература). — ISBN 978-5-8114-1003-3.
• Большая Советская Энциклопедия / Гл. ред. А. М. Прохоров. — 3-е изд. — М.: Советская Энциклопедия, 1976. — Т. 25: Струнино — Тихорецк. — 600 с. Архивная копия от 5 августа 2017 на Wayback Machine
• Борщевский А. Я. Физическая химия. Том 1 online. Общая и химическая термодинамика. — М: Инфра-М, 2017. — 868 с. — ISBN 978-5-16-104227-4.
• Бурдаков В. П., Дзюбенко Б. В., Меснянкин С. Ю., Михайлова Т. В. Термодинамика. Часть 2. Специальный курс. — М.: Дрофа, 2009. — 362 с. — (Высшее образование. Современный учебник). — ISBN 978-5-358-06140-8.
• Жариков В. А. Основы физической геохимии. — М.: Наука; Изд-во МГУ, 2005. — 656 с. — (Классический университетский учебник). — ISBN 5-211-04849-0, 5-02-035302-7.
• Залевски К. Феноменологическая и статистическая термодинамика: Краткий курс лекций / Пер. с польск. под. ред. Л. А. Серафимова. — М.: Мир, 1973. — 168 с.
• Карякин Н. В. Основы химической термодинамики. — М.: Академия, 2003. — 463 с. — (Высшее профессиональное образование). — ISBN 5-7695-1596-1. (недоступная ссылка)
• Кнорре Д. Г., Крылова Л. Ф., Музыкантов В. С. Физическая химия. — 2. — М.: Высшая школа, 1990. — 416 с. — ISBN 5-06-000655-7.
• Кубо Р. Термодинамика. — М.: Мир, 1970. — 304 с.
• Ляшков В. И. Теоретические основы теплотехники. — М.: Курс; Инфра-М, 2015. — 328 с. — ISBN 978-5-905554-85-8, 978-5-16-0І0639-7.
• Морачевский А. Г., Кохацкая М. С. Прикладная химическая термодинамика. — СПб.: Изд-во Политехн. ун-та, 2008. — 254 с. — ISBN 978-5-7422-2006-0.
• Морачевский А. Г., Фирсова Е. Г. Физическая химия. Термодинамика химических реакций. — 2-е изд., испр. — СПб.: Лань, 2015. — 101 с. — (Учебники

для вузов. Специальная литература). — ISBN 978-5-8114-1858-9. (недоступная ссылка)

• Мюнстер А. Химическая термодинамика / Пер. с нем. под. ред. чл.-корр. АН СССР Я. И. Герасимова. — М.: Мир, 1971. — 296 с.
• Нараев В. Н. Физическая химия. Часть 1. Химическая термодинамика. Фазовые равновесия и учение о растворах. Электрохимия. — СПб.: Санкт-Петербургский государственный технологический институт (Технический университет), 2007. — 262 с. (недоступная ссылка)
• Никольский Б. П., Смирнова Н. А., Панов М. Ю. и др. Физическая химия. Теоретическое и практическое руководство / Под ред. Б. П. Никольского. — 2-е изд., перераб. и доп. — Л.: Химия, 1987. — 880 с. — (Для высшей школы).
• Путилов К. А. Термодинамика / Отв. ред. М. Х. Карапетьянц. — М.: Наука, 1971. — 376 с.
• Степановских Е. И., Брусницына Л. А., Маскаева Л. Н. Химическая термодинамика в вопросах и ответах. — Екатеринбург: УИПЦ, 2014. — 221 с. — ISBN 978-5-4430-0061-9.
• Сычёв В. В. Сложные термодинамические системы. — 5-е изд., перераб. и доп. — М.: Издательский дом МЭИ, 2009. — 296 с. — ISBN 978-5-383-00418-0.
• Тамм М. Е., Третьяков Ю. Д. Неорганическая химия. Том 1. Физико-химические основы неорганической химии / Под. ред. акад. Ю. Д. Третьякова. — М.: Академия, 2004. — 240 с. — (Высшее профессиональное образование). — ISBN 5-7695-1446-9.
• Термодинамика. Основные понятия. Терминология. Буквенные обозначения величин / Отв. ред. И. И. Новиков. — АН СССР. Комитет научно-технической терминологии. Сборник определений. Вып. 103. — М.: Наука, 1984. — 40 с.
• Химическая энциклопедия / Гл. ред. Н. С. Зефиров. — М.: Большая Российская энциклопедия, 1995. — Т. 4: Пол — Три. — 640 с. — ISBN 5-85270-092-4.
• Химический энциклопедический словарь / Гл. ред. И. Л. Кнунянц. — М.: Советская энциклопедия, 1983. — 792 с.
• Шмидт Э. Введение в техническую термодинамику / Пер. с нем. — М.—Л.: Энергия, 1965. — 392 с.
• Эткинс П. Физическая химия. — М.: Мир, 1980.

Теплота — Википедия

Внутренняя энергия термодинамической системы может изменяться двумя способами: посредством совершения работы над системой и посредством теплообмена с окружающей средой. Энергия, которую получает или теряет тело в процессе теплообмена с окружающей средой, называется коли́чеством теплоты́ или просто теплотой^[1]. Теплота — это одна из основных термодинамических величин в классической феноменологической термодинамике. Количество теплоты входит в стандартные математические формулировки первого и второго начал термодинамики.

Для изменения внутренней энергии системы посредством теплообмена также необходимо совершить работу. Однако это не механическая работа, которая связана с перемещением границы макроскопической системы. На микроскопическом уровне эта работа осуществляется силами, действующими между молекулами на границе контакта более нагретого тела с менее нагретым. Фактически при теплообмене энергия передаётся посредством электромагнитного взаимодействия при столкновениях молекул. Поэтому с точки зрения молекулярно-кинетической теории различие между работой и теплотой проявляется только в том, что совершение механической работы требует упорядоченного движения молекул на макроскопических масштабах, а передача энергии от более нагретого тела менее нагретому этого не требует.

Энергия может также передаваться излучением от одного тела к другому и без их непосредственного контакта.

Количество теплоты не является функцией состояния, и количество теплоты, полученное системой в каком-либо процессе, зависит от способа, которым она была переведена из начального состояния в конечное.

Единица измерения в Международной системе единиц (СИ) — джоуль. Как единица измерения теплоты используется также калория. В Российской Федерации калория допущена к использованию в качестве внесистемной единицы без ограничения срока с областью применения «промышленность»^[2].

Количество теплоты входит в математическую формулировку первого начала термодинамики, которую можно записать как Q=A+ΔU{\displaystyle Q=A+\Delta U}. Здесь ΔU{\displaystyle \Delta U} — изменение внутренней энергии системы, Q{\displaystyle Q} — количество теплоты, переданное системе, а A{\displaystyle A} — работа, совершённая системой. Однако определение теплоты должно указывать способ её измерения безотносительно к первому началу. Так как теплота — это энергия переданная в ходе теплообмена, для измерения количества теплоты необходимо пробное калориметрическое тело. По изменению внутренней энергии пробного тела можно будет судить о количестве теплоты, переданном от системы пробному телу. Без использования пробного тела первое начало теряет смысл содержательного закона и превращается в бесполезное для расчётов определение количества теплоты.

Пусть в системе, состоящей из двух тел X{\displaystyle X} и Y{\displaystyle Y}, тело Y{\displaystyle Y} (пробное) заключено в жёсткую адиабатическую оболочку. Тогда оно не способно совершать макроскопическую работу, но может обмениваться энергией (то есть теплотой) с телом X{\displaystyle X}. Предположим, что тело X{\displaystyle X} также почти полностью заключено в адиабатическую, но не жёсткую оболочку, так что оно может совершать механическую работу, но обмениваться теплотой может лишь с Y{\displaystyle Y}. Количеством теплоты, переданным телу X{\displaystyle X} в некотором процессе, называется величина QX=−ΔUY{\displaystyle Q_{X}=-\Delta U_{Y}}, где ΔUY{\displaystyle \Delta U_{Y}} — изменение внутренней энергии тела Y{\displaystyle Y}. Согласно закону сохранения энергии, полная работа, выполненная системой, равна убыли полной внутренней энергии системы двух тел: A=−ΔUx−ΔUy{\displaystyle A=-\Delta U_{x}-\Delta U_{y}}, где A{\displaystyle A} — макроскопическая работа, совершенная телом X{\displaystyle X}, что позволяет записать это соотношение в форме первого начала термодинамики:Q=A+ΔUx{\displaystyle Q=A+\Delta U_{x}}.

Таким образом, вводимое в феноменологической термодинамике количество теплоты может быть измерено посредством калориметрического тела (об изменении внутренней энергии которого можно судить по показанию соответствующего макроскопического прибора). Из первого начала термодинамики следует корректность введённого определения количества теплоты, то есть независимость соответствующей величины от выбора пробного тела Y{\displaystyle Y} и способа теплообмена между телами. При таком определении количества теплоты первое начало становится содержательным законом, допускающим экспериментальную проверку, так как все три величины, входящие в выражение для первого начала, могут быть измерены независимо^[3].

Предположим, что рассматриваемое тело может обмениваться теплотой лишь с N{\displaystyle N} бесконечными тепловыми резервуарами, внутренняя энергия которых столь велика, что при рассматриваемом процессе температура каждого остаётся строго постоянной. Предположим, что над телом был совершён произвольный круговой процесс, то есть по окончании процесса оно находится абсолютно в том же состоянии, что и в начале. Пусть при этом за весь процесс оно заимствовало из i-го резервуара, находящегося при температуре Ti{\displaystyle T_{i}}, количество теплоты Qi{\displaystyle Q_{i}}. Тогда верно следующее неравенство Клаузиуса:

∘∑i=1NQiTi⩽0.{\displaystyle \circ \sum _{i=1}^{N}{\frac {Q_{i}}{T_{i}}}\leqslant 0.}

Здесь ∘{\displaystyle \circ } обозначает круговой процесс. В общем случае теплообмена со средой переменной температуры неравенство принимает вид

∮⁡δQ(T)T⩽0.{\displaystyle \oint {\frac {\delta Q(T)}{T}}\leqslant 0.}

Здесь δQ(T){\displaystyle \delta Q(T)} — количество теплоты, переданное участком среды с (постоянной) температурой T{\displaystyle T}. Это неравенство применимо для любого процесса, совершаемого над телом. В частном случае квазистатического процесса оно переходит в равенство. Математически это означает, что для квазистатических процессов можно ввести функцию состояния, называемую энтропией, для которой

S=∫δQ(T)T,{\displaystyle S=\int {\frac {\delta Q(T)}{T}},}

dS=δQT.{\displaystyle dS={\frac {\delta Q}{T}}.}

Здесь T{\displaystyle T} — это абсолютная температура внешнего теплового резервуара. В этом смысле 1T{\displaystyle {\frac {1}{T}}} является интегрирующим множителем для количества теплоты, умножением на который получается полный дифференциал функции состояния.

Для неквазистатических процессов такое определение энтропии не работает. Например, при адиабатическом расширении газа в пустоту

∫δQ(T)T=0,{\displaystyle \int {\frac {\delta Q(T)}{T}}=0,}

однако энтропия при этом возрастает, в чём легко убедиться, переведя систему в начальное состояние квазистатически и воспользовавшись неравенством Клаузиуса. Кроме того, энтропия (в указанном смысле) не определена для неравновесных состояний системы, хотя во многих случаях систему можно считать локально равновесной и обладающей некоторым распределением энтропии.

Внутренняя энергия системы, в которой возможны фазовые переходы или химические реакции, может изменяться и без изменения температуры. Например, энергия, передаваемая в систему, где жидкая вода находится в равновесии со льдом при нуле градусов Цельсия, расходуется на плавление льда, но температура при этом остаётся постоянной, пока весь лёд не превратится в воду. Такой способ передачи энергии традиционно называется «скрытой» или изотермической теплотой^[4] (англ. latent heat), в отличие от «явной», «ощущаемой» или неизотермической теплоты (англ. sensible heat), под которой подразумевается процесс передачи энергии в систему, в результате которого изменяется лишь температура системы, но не её состав.

Энергия, необходимая для фазового перехода единицы массы вещества, называется удельной теплотой фазового превращения^[5]. В соответствии с физическим процессом, имеющим место при фазовом превращении, могут выделять теплоту плавления, теплоту испарения, теплоту сублимации (возгонки), теплоту перекристаллизации и т. д. Фазовые превращения идут со скачкообразным изменением энтропии, что сопровождается выделением или поглощением тепла, несмотря на постоянство температуры.

О терминах «теплота», «количество теплоты», «тепловая энергия»[править | править код]

Многие понятия термодинамики возникли в связи с устаревшей теорией теплорода, которая сошла со сцены после выяснения молекулярно-кинетических основ термодинамики. С тех пор они используются и в научном, и в повседневном языке. Хотя в строгом смысле теплота представляет собой один из способов передачи энергии, и физический смысл имеет лишь количество энергии, переданное системе, слово «тепло-» входит в такие устоявшиеся научные понятия, как поток тепла, теплоёмкость, теплота фазового перехода, теплота химической реакции, теплопроводность и пр. Поэтому там, где такое словоупотребление не вводит в заблуждение, понятия «теплота» и «количество теплоты» синонимичны^[6]. Однако этими терминами можно пользоваться только при условии, что им дано точное определение, не связанное с представлениями теории теплорода, и ни в коем случае «количество теплоты» нельзя относить к числу первоначальных понятий, не требующих определения^[7]. Поэтому некоторые авторы уточняют, что во избежание ошибок теории теплорода под понятием «теплота» следует понимать именно способ передачи энергии, а количество переданной этим способом энергии обозначают понятием «количество теплоты»^[8]. Рекомендуется избегать такого термина, как «тепловая энергия», который по смыслу совпадает с внутренней энергией^[9].

Выработка энергопредприятиями тепловой и электрической энергии[править | править код]

В связи с зависимостью выработки электроэнергии от выработки тепла паросиловыми установками выделяют несколько видов выработки тепла и электроэнергии.

1. Раздельная выработка тепла и электроэнергии.
2. Комбинированная выработка тепла и электроэнергии.

Последний тип получения тепловой и электроэнергии является основой теплофикации, и характеризуется как совершенный метод производства энергии.^[10]

1. ↑ Сивухин, 2005, с. 57.
2. ↑ Положение о единицах величин, допускаемых к применению в Российской Федерации. Утверждено Постановлением Правительства РФ от 31 октября 2009 г. № 879. (неопр.) (недоступная ссылка). Дата обращения 16 февраля 2014. Архивировано 2 ноября 2013 года.
3. ↑ Сивухин, 2005, с. 58.
4. ↑ Путилов, 1971, с. 49.
5. ↑ Сивухин, 2005, с. 442.
6. ↑ Теплота / Мякишев Г. Я. // Струнино — Тихорецк. — М. : Советская энциклопедия, 1976. — (Большая советская энциклопедия : [в 30 т.] / гл. ред. А. М. Прохоров ; 1969—1978, т. 25).
7. ↑ Сивухин, 2005, с. 13.
8. ↑ Базаров, 1991, с. 25.
9. ↑ Сивухин, 2005, с. 61.
10. ↑ Энергосбережение в теплоэнергетике и теплотехнологиях: учебное пособие / Л.И. Молодежникова; Томский политехнический университет. — Томск: Изд-во Томского политехнического университета, 2011. – С.43-45.

• Базаров И. П. Термодинамика. — М.: Высшая школа, 1991. — 376 с.
• Путилов К. А. Термодинамика. — М.: Наука, 1971. — 375 с.
• Сивухин Д. В. Общий курс физики. — Т. II. Термодинамика и молекулярная физика. — 5 изд., испр.. — М.: Физматлит, 2005. — 544 с. — ISBN 5-9221-0601-5.

Тепловые процессы Основные понятия и определения теории теплообмена

Тепловые процессы Основные понятия и определения теории теплообмена

Основы теплообмена § Самопроизвольный необратимый процесс переноса § § § энергии в форме теплоты в пространстве называют теплообменом. Существует три основных вида теплообмена: теплообмен теплопроводностью, конвективный теплообмен, теплообмен излучением. Теплообмен очень часто сопровождается массобменом. . Если концентрации компонентов в различных точках пространства разные, происходит необратимый перенос массы компонентов из одной области в другую. Этот процесс называется массообменом. Совместно протекающий процесс переноса теплоты и массы вещества называют тепломассообменом. Как и любой реальный самопроизвольный процесс тепломассообмен является необратимым и продолжается до тех пор, пока в системе не установится термодинамическое равновесие.

Теплопроводность § Перенос энергии (теплоты) при непосредственном § § § контакте более нагретых элементов тела (или среды) с менее нагретыми, осуществляемый посредством хаотического движения микрочастиц (молекул, атомов, электронов, ионов), называют теплопроводностью. Материалы обладают различной способностью проводить теплоту. Наибольшей способностью обладают металлы. Их теплопроводность при не очень низких температурах в основном обуславливается тепловым движением электронов. Причем, чем меньше удельное электрическое сопротивление металла, тем выше его теплопроводность.

Теплопроводность § Газы плохие проводники теплоты. Теплопроводность газов обусловлена хаотическим тепловым движением молекул. Она возрастает с увеличением температуры, так как при этом увеличивается скорость теплового движения молекул. § В диэлектриках передача теплоты происходит посредством колебаний узлов кристаллической решетки, а в жидкостях — за счет упругих колебаний молекул и их перескока из одного положения в другое.

Конвективный теплообмен В движущихся жидкостях и газах происходит конвективный теплообмен. В этом случае распространение энергии в пространстве осуществляется одновременно двумя способами: § за счет теплового движения микрочастиц и § посредством перемешивания микрочастиц (элементов жидкости или газа) из одной точки пространства в другую. Последний способ называют конвективным переносом теплоты.

Конвективный теплообмен Перенос тепла возможен в условиях естественной (свободной) или вынужденной конвекции. Естественная конвекция происходит, например, за счет разности плотностей в различных точках объема жидкости (или газа), возникшей вследствие разности температур в этих точках (термогравитационная конвекция). Вынужденная конвекция происходит под действием внешних сил принудительном движении всего объема жидкости (или газа). Возможен также теплообмен при смешанной конвекции. Конвективный теплообмен между движущейся средой и омываемой ею поверхностью твердого тела называют теплоотдачей.

Теплообмен излучением (радиационный теплообмен) Третий вид теплообмена — теплообмен излучением включает в себя совокупность процессов: § превращение внутренней энергии вещества в энергию излучения (энергию электромагнитных волн или фотонов) – процесс лучеиспускания; § перенос излучения; § поглощение излучения веществом – процесс лучепоглощения.

Сложные виды теплообмена Перенос энергии одновременно § излучением и § теплопроводностью называется радиационно-кондуктивным теплообменом, Перенос энергии одновременно § излучением, § теплопроводностью и § конвекцией называется радиационно-конвективным теплообменом.

Особенности описания тепломассопереноса Для теоретического изучения процессов тепломассопереноса на основе общих законов физики составляется их математическое описание. При этом среду, в которой протекают эти процессы, считают сплошной. Это значит, что в физически бесконечно малом элементе V (элементарном объеме) содержится очень большое число микрочастиц. Под V понимается такой объем, размеры которого пренебрежимо малы по сравнению с характерным геометрическим размером (например, с диаметром трубы).

ТАКИМ ОБРАЗОМ Перенос энергии в форме теплоты может осуществляться тремя способами: § теплопроводностью; § конвекцией; § излучением (радиацией). Совокупность всех трех видов теплообмена называется сложным теплообменом.

Еще термины… • Горячее тело или вещество, участвующее в процессе теплообмена называют горячим теплоносителем. • Нагреваемое вещество называют холодным теплоносителем. • Чаще всего теплота передается через стенку, разделяющую теплоносители. Эту стенку называют поверхностью теплообмена.

МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ ПРОЦЕССА ТЕПЛОПРОВОДНОСТИ В начале введем некоторые понятия, которыми будем оперировать при описании процесса теплопередачи теплопроводностью: — температурное поле; — градиент температуры; — тепловой поток — коэффициент теплопроводности — коэффициент температуропроводности 12

Температурное поле К числу основных задач теплообмена относится установление зависимости между тепловым потоком и распределением температур в средах. Совокупность значений температуры в данный момент времени для всех точек изучаемого пространства называется температурным полем. В зависимости от конфигурации изучаемой области пространства (т. е. от формы тела) выбирают декартову, цилиндрическую или сферическую системы координат. 13

Системы координат

Нестационарное и стационарное температурное поле Для декартовой системы координат: Т = f(x, y, z, t) (1) где: § T –температура тела; § x, y, z -координаты точки; § t — время. Такое температурное поле называется нестационарным, т. е. соответствует неустановившемуся тепловому режиму теплопроводности. Если температура тела функция только координат и не изменяется с течением времени, то температурное поле называется стационарным: T = f(x, y, z) , ∂T/∂t = 0 (2) 15

Уравнения температурного поля Уравнение двухмерного температурного поля: § для нестационарного режима: T = f(x, y, t) ; ∂T/∂z = 0 (3) § для стационарного режима: T = f(x, y) , ∂T/∂z = 0; ∂T/∂t = 0 (4) Уравнение одномерного температурного поля: § для нестационарного режима: T = f(x, t) ; ∂T/∂y = ∂T/∂z = 0 ( 5) § для стационарного режима: T = f(x) ; ∂T/∂y = ∂T/∂z = 0; ∂T/∂t = 0 (6) 16

Изотермы Поверхность, во всех точках которой температура одинакова, называют изотермической. В плоскости пересечения тела эти поверхности оставляют следы в виде изотерм — линий одинаковой температуры. 17

Градиент температуры Градиентом температуры называют предел отношения изменения температуры ∆T к расстоянию между изотермами по нормали ∆n, когда ∆n стремится к нулю: |grad. T| = lim[∆T/∆n]∆n→ 0 = ∂T/∂n Градиент температуры – это вектор, направленный по нормали к изотермической поверхности в сторону возрастания температуры и численно равный производной температуры Т по этому направлению: grad. Т = (∂Т/∂n)·no (7) где: no – единичный вектор. 18

Тепловой поток § Количество теплоты, проходящее через изотермическую поверхность F в единицу времени называют тепловым потоком – Q, [Вт = Дж/с]. § Тепловой поток, проходящий через единицу площади называют плотностью теплового потока q = Q/F, [Вт/м 2] 19

Закон Фурье для теплопроводности Для твердого тела уравнение теплопроводности подчиняется закону Фурье: Тепловой поток, передаваемый теплопроводностью, пропорционален градиенту температуры и площади сечения, перпендикулярного направлению теплового потока: Q = -λ∙F∙ ∂Т/∂n (8) или q = -λ∙(∂Т/∂n)∙no = -λ∙grad. Т (9) где: q – вектор плотности теплового потока; 20

Коэффициент теплопроводности § Коэффициент теплопроводности является физическим параметром вещества, характеризующим способность тела проводить теплоту. § зависит от природы вещества, давления и температуры. Также на его величину влияет влажность вещества. Кирпич красный 0, 70 Серебро 420 § Коэффициенты теплопроводности некоторых Вода 0, 683 Медь 395 веществ , Вт/(м. Водород 273 К К), при 0, 172 Алюминий 207 Гелий 0, 143 Латунь (67 % Сu, 33 % Zn) 101 Кирпич диатомитовый Сталь 20 55 Кирпич пеношамотный Бетон сухой 0, 84 Воздух 0, 0244 0, 113 0, 100 21

Коэффициент температуропроводности а — физическое свойство вещества, от которого зависит скорость изменения температуры в нестационарных процессах теплопроводности. Чем больше а, тем быстрее тело охлаждается или нагревается Определяется по формуле: где — удельная теплоёмкость Значения а для некоторых веществ § Медь (Т= 273 К) § Воздух (Т= 273 К, р = 0, 101 МПа) § Сталь 20 (Т = 273 К) § Нержавеющая сталь Х 18 Н 9 Т § Вода (Т= 373 К, р = 0, 101 МПа) а 105 м 2/с 11, 6 1, 88 1, 16 0, 363 0, 0169 22

Дифференциальное уравнение температурного поля (уравнение Фурье) (без источников / стоков тепла) Дифференциальное уравнение, описывающее температурное поле в теле (в неподвижной среде) без внутренних источников (стоков) тепла, в любой момент времени в прямоугольной системе координат имеет вид: или через оператор Лапласа Это уравнение называется уравнением Фурье 23

Стационарная теплопроводность Для установившегося процесса передачи тепла (стационарный процесс) дифференциальное уравнение Фурье имеет вид: или через оператор Лапласа 24

Условия однозначности для уравнения теплопроводности Для решения этих дифференциальных уравнений Фурье должны быть заданы следующие дополнительные условия (условия однозначности): § 1) геометрические условия, характеризующие форму и размеры тела; § 2) физические условия, характеризующие физические свойства тела ( , С, …) и их зависимость от температуры; § 3) начальные условия, т. е. температурное поле в теле в начальный момент времени. В частности, температура тела в момент времени t = 0 может быть задана как постоянная величина для всех точек тела. 25 Для стационарной теплопроводности начальные условия не имеют смысла

Условия однозначности для уравнения теплопроводности (продолжение) § 4) Граничные условия, характеризующие воздействие окружающей среды на поверхность тела. Эти условия могут быть сформулированы различными способами: § а) граничные условия первого рода – задается температура в каждой точке поверхности тела в любой момент времени. T = f(x, y, z, τ) В простейшем случае температура может быть задана как постоянная величина во всех её точках и не меняться во времени; § б) граничные условия второго рода – задается плотность теплового потока в каждой точке поверхности 26 в любой момент времени q = f(x, y, z, τ)

Условия однозначности для уравнения теплопроводности (продолжение) в) граничные условия третьего рода линейные – задается температура окружающей среды Тж и закон теплообмена между поверхностью и окружающей средой (для конвективного теплообмена) в виде закона Ньютона Рихмана. Принято записывать линейные граничные условия третьего рода в форме уравнения где закона сохранения энергии для — коэффициент теплоотдачи, Вт/(м 2 К). поверхности тела 27

Условия однозначности для уравнения теплопроводности (продолжение) § г) граничные условия третьего рода нелинейные – задается температура окружающей среды и закон теплообмена между поверхностью и окружающей средой осуществляющийся излучением Это уравнение Стефана-Больцмана, где Спр – приведённый коэффициент излучения [Вт/(м 2 К 4] В общем случае при граничных условиях третьего рода температура Тж и коэффициент теплоотдачи могут меняться во времени, а также при переходе от одной точки 28 поверхности к другой.

Способы задания граничных условий Граничные условия первого рода Распределение температуры на поверхности тела Граничные условия второго рода Распределение плотности теплового потока на поверхности тела Граничные Условия теплообмена условия поверхности тела с третьего рода окружающей средой: – линейные — конвективный; — нелинейные — излучением. T = f(x, y, z, τ) q = α(Тж– Тп) = = -λ∙ ∂Т/∂n│n→ 0 29

Стационарная теплопроводность и теплопередача в твёрдых телах 30

Плоская стенка с граничными условиями 1 -го рода § Однослойная стенка с коэфф. теплопроводности λ = const. § Плоская стенка, толщина (по оси х) которой существенно меньше её протяженности по y и z. § Тепловой поток можно принять одномерным в направлении x. По уравнению Фурье имеем: Двойное интегрирование приводит к функции, которая показывает, что по толщине температура изменяется прямолинейно. 31 где С 1 и С 2 — константы интегрирования

Плоская стенка с граничными условиями 1 -го рода (продолжение) При граничных условиях первого рода заданы температуры на границах стенки: § При x = 0 § T = Tn 1 ; § при x = § T = Tn 2 Получаем константы интегрирования § С 2 = Т n 1, § C 1 = (Tn 2 – Tn 1)/ § Тогда температура тела в точке с координатой х: 32

Плоская стенка с граничными условиями 1 -го рода или с другим направление теплового потока 33 По толщине стенки температура изменяется прямолинейно

Плотность теплового потока для плоской стенки с граничными условиями 1 рода § Для однородной плоской стенки толщиной , коэффициент теплопроводности которой равен [Вт/(м К)], и не зависит от температуры, плотность теплового потока q определяется по формуле: Обозначим R — термическое сопротивление Тогда получаем: 34

Многослойная стенка при l = const с граничными условиями 1 -го рода Стенка состоит из последовательно расположенных слоев толщиной i и теплопроводности i общая толщина стенки существенно меньше остальных размеров (y и z). Так как тепловой поток постоянен, то: 35

Плотность тепловых потоков многослойную стенку при l = const с граничными условиями 1 -го рода Плотности тепловых потоков через каждый слой стенки: § q = λ 1/δ 1∙(Тn 1 – Тn 2) § q = λ 2/δ 2∙(Тn 2 – Тn 3) § q = λ 3/δ 3∙(Тn 3 – Тn 4). . . …………. Складывая левые и правые части получаем: 36

§ Температуры на границе раздела слоев 1 и 2 стенки при условии идеального контакта между ними можно определить по формуле: § Распределение температуры в многослойной стенке при λ = const с граничными условиями 1 -го рода 37

Плоская стенка с граничными условиями 3 -го рода Практически важным является процесс, в котором известными считаются величины, входящие в граничные условия третьего рода: § температуры жидкостей Тж 1 и Тж 2 с двух сторон стенки; § коэффициенты теплоотдачи со стороны первой a 1 и со стороны второй a 2 жидкостей. 38

Закон Ньютона-Рихмана Процесс теплообмена между поверхностью тела и средой описывается законом Ньютона-Рихмана, который гласит, что количество теплоты, передаваемой конвективным теплообменом прямо пропорционально разности температур поверхности тела (Тс) и окружающей среды (Тж): Q = α(Тс — Тж)·F (1) или q = α(Тс — Тж) (2) где: α — коэффициент теплоотдачи [Вт/(м 2 К)], характеризует интенсивность теплообмена между поверхностью тела и окружающей средой. 39

Теплопередача и три Процесс переноса теплоты от одной жидкости термических сопротивления к другой через разделяющую их стенку называется теплопередачей. Процессу теплопередачи препятствуют три термических сопротивления: § внутреннее R = d/ (для многослойной стенки оно равно сумме термических сопротивлений слоев): 40

Внешние термические сопротивления (3) (4) Здесь Тс1 — температура поверхности стенки, соприкасающейся с первой жидкостью, Тс2 — температура поверхности, соприкасающейся со второй жидкостью. Внешние термические сопротивления это термические сопротивления 41

§ Имеем систему трех уравнений с неизвестными Тс1, Тс2 и q. § Если эти три уравнения сложить, то неизвестные Тс1 и Тс2 сокращаются. § В результате получим уравнение плотности теплового потока: (5) 42

Коэффициент теплопередачи § Отношение плотности теплового потока q к температурному напору T = Тж 1 — Tж 2 называют коэффициентом теплопередачи k [Вт/(м К)]: k = q / T Из (5) следует, что для однослойной плоской стенки коэффициент теплопередачи: Для однослойной плоской стенки: 43

Коэффициент теплопередачи § Коэффициент теплопередачи k характеризует интенсивность процесса теплопередачи. § В соответствие с формулой k = q / T он численно равен плотности теплового потока, передаваемого через стенку при температурном напоре, равном единице. § Это величина, обратная сумме всех термических сопротивлений § Если одно из сопротивлений значительно больше всех остальных, то практически оно одно и будет определять 44 значение коэффициента теплопередачи.

тепловой процесс — это… Что такое тепловой процесс?



тепловой процесс

 

тепловой процесс
—
[А.С.Гольдберг. Англо-русский энергетический словарь. 2006 г.]

Тематики

• энергетика в целом

Справочник технического переводчика. – Интент. 2009-2013.

• тепловой пробой p-n перехода
• тепловой пункт

Смотреть что такое «тепловой процесс» в других словарях:

• Тепловой процесс — Тепловые процессы …   Википедия

• тепловой процесс — šiluminis vyksmas statusas T sritis fizika atitikmenys: angl. heat process vok. Wärmevorgang, m rus. тепловой процесс, m pranc. processus thermique, m …   Fizikos terminų žodynas

• тепловой процесс — šiluminis procesas statusas T sritis Energetika apibrėžtis Termodinaminis prosesas, kada termodinaminės būsenos parametrai keičiasi dėl sistemai teikiamos ar atimamos šilumos. atitikmenys: angl. heat process vok. Wärmevorgang, m rus. тепловой… …   Aiškinamasis šiluminės ir branduolinės technikos terminų žodynas

• Тепловой процесс —         термодинамический процесс, изменение состояния физической системы (рабочего тела (См. Рабочее тело)) в результате теплообмена и совершения работы. Если Т. п. протекает настолько медленно, что в каждый момент рабочее тело будет находиться… …   Большая советская энциклопедия

• Процесс — (Process) Определение процесса, виды и типы процессов Информация об определении процесса, виды и типы процессов Содержание Содержание Определение Исторический Бизнес процесс Тепловой процесс Адиабатический процесс Изохорный процесс Изобарный… …   Энциклопедия инвестора

• Тепловой баланс — I Тепловой баланс         сопоставление прихода и расхода (полезно использованной и потерянной) теплоты в различных тепловых процессах (См. Тепловой процесс). В технике Т. б. используется для анализа тепловых процессов, осуществляющихся в паровых …   Большая советская энциклопедия

• Процесс — По теме Процесс должна быть отдельная статья, а не страница разрешения неоднозначностей. После создания основной статьи страницу разрешения неоднозначностей, если в ней будет необходимость, переименуйте в Процесс (значения). Содержание 1… …   Википедия

• Тепловой эффект химической реакции — или изменение энтальпии системы вследствие протекания химической реакции  отнесенное к изменению химической переменной количество теплоты, полученное системой, в которой прошла химическая реакция и продукты реакции приняли температуру… …   Википедия

• Процесс Фишера — Тропша — Процесс Фишера – Тропша  это химическая реакция, происходящая в присутствии катализатора, в которой монооксид углерода (CO) и водород h3 преобразуются в различные жидкие углеводороды. Обычно используются катализаторы, содержащие железо и… …   Википедия

• Процесс Фишера — Тропа — Процесс Фишера  Тропша  это химическая реакция, происходящая в присутствии катализатора, в которой монооксид углерода (CO) и водород h3 преобразуются в различные жидкие углеводороды. Обычно используются катализаторы, содержащие железо и кобальт.… …   Википедия

Книги

• Высококвалифицированная швея, Н. В. Горшкова. Рассмотрены ассортимент и свойства современных материалов для изготовления швейных изделий, особенности их конструирования в зависимости от используемых материалов, декоративной отделки… Подробнее  Купить за 546 руб
• Сушка и увлажнение лубоволокнистых материалов. Учебник, В. А. Суметов. Описаны свойства обрабатывающей среды, характеристика влажных материалов, способы сушки и их сущность, теоретические основы конвективной сушки, тепловой расчет воздушных… Подробнее  Купить за 340 руб
• Готовим в горшочках, Л. А. Калугина. Глиняный горшок — самая древняя кухонная посуда. Поэтому, несмотря на огромный арсенал современной посуды, в обществе снова возник интерес к глиняным горшочкам, т. е. интерес к более… Подробнее  Купить за 294 руб

Другие книги по запросу «тепловой процесс» >>

процесс тепловой — это… Что такое процесс тепловой?



процесс тепловой

працэс цеплавы

Русско-белорусский словарь математических, физических и технических терминов. 2013.

• процесс телеобработки данных
• процесс теплообмена

Смотреть что такое «процесс тепловой» в других словарях:

• Процесс — (Process) Определение процесса, виды и типы процессов Информация об определении процесса, виды и типы процессов Содержание Содержание Определение Исторический Бизнес процесс Тепловой процесс Адиабатический процесс Изохорный процесс Изобарный… …   Энциклопедия инвестора

• Тепловой эффект химической реакции — или изменение энтальпии системы вследствие протекания химической реакции  отнесенное к изменению химической переменной количество теплоты, полученное системой, в которой прошла химическая реакция и продукты реакции приняли температуру… …   Википедия

• Процесс Фишера — Тропша — Процесс Фишера – Тропша  это химическая реакция, происходящая в присутствии катализатора, в которой монооксид углерода (CO) и водород h3 преобразуются в различные жидкие углеводороды. Обычно используются катализаторы, содержащие железо и… …   Википедия

• Процесс Фишера — Тропа — Процесс Фишера  Тропша  это химическая реакция, происходящая в присутствии катализатора, в которой монооксид углерода (CO) и водород h3 преобразуются в различные жидкие углеводороды. Обычно используются катализаторы, содержащие железо и кобальт.… …   Википедия

• процесс выработки электрической или тепловой энергии с использованием отходов — — [А.С.Гольдберг. Англо русский энергетический словарь. 2006 г.] Тематики энергетика в целом EN waste to energy process …   Справочник технического переводчика

• тепловой процесс — — [А.С.Гольдберг. Англо русский энергетический словарь. 2006 г.] Тематики энергетика в целом EN thermal process …   Справочник технического переводчика

• Тепловой разгон аккумулятора — Тепловой разгон аккумулятора  явление, при котором ЭДС электрического аккумулятора резко падает,[источник не указан 485 дней] и, поскольку внутреннее сопротивление аккумулятора обычно… …   Википедия

• тепловой баланс (металлургия) — тепловой баланс Кол в, равенство прихода и расхода теплоты в к. л. тепловом процессе. В основе уравнений т. б. любого металлургич. агрегата лежит закон сохранения энергии, согласно к рому кол во теплоты, поступ. в данный процесс, равно кол ву… …   Справочник технического переводчика

• тепловой сток — Процесс переноса тепла вместе с речными водами …   Словарь по географии

• Процесс — [лат. processus про движение] ход какого либо явления, последовательная смена состояний или совокупность действий для достижения заданной цели: адиабатический протекающий в отсутствие теплообмена с окружающей средой; изотермический протекающий… …   Энциклопедия терминов, определений и пояснений строительных материалов

• Тепловой процесс — Тепловые процессы …   Википедия

Книги

• Высококвалифицированная швея, Н. В. Горшкова. Рассмотрены ассортимент и свойства современных материалов для изготовления швейных изделий, особенности их конструирования в зависимости от используемых материалов, декоративной отделки… Подробнее  Купить за 546 руб
• Сушка и увлажнение лубоволокнистых материалов. Учебник, В. А. Суметов. Описаны свойства обрабатывающей среды, характеристика влажных материалов, способы сушки и их сущность, теоретические основы конвективной сушки, тепловой расчет воздушных… Подробнее  Купить за 340 руб
• Готовим в горшочках, Л. А. Калугина. Глиняный горшок — самая древняя кухонная посуда. Поэтому, несмотря на огромный арсенал современной посуды, в обществе снова возник интерес к глиняным горшочкам, т. е. интерес к более… Подробнее  Купить за 294 руб

Другие книги по запросу «процесс тепловой» >>