3. Факторы, влияющие на емкость конденсатора | 12. Конденсаторы | Часть1
Факторы, влияющие на емкость конденсатора
На емкость конденсатора влияют три основных фактора.
ПЛОЩАДЬ ПЛАСТИН: При прочих равных условиях, большая площадь пластин даст большую ёмкость, а меньшая — меньшую.
Объяснение: большая площадь пластин приводит к увеличению заряда, накапливаемого на пластинах для данного электрического поля (напряжения между пластинами).
РАССТОЯНИЕ МЕЖДУ ПЛАСТИНАМИ: При прочих равных условиях, большее расстояние дает меньшую емкость и наоборот.
Объяснение: меньшее расстояние создает большую силу поля (напряжение, деленное на расстояние между пластинами), что приводит к накоплению большего заряда для любого заданного напряжения.
ДИЭЛЕКТРИЧЕСКИЙ МАТЕРИАЛ: При прочих равных условиях, материал с большей относительной диэлектрической проницаемостью дает большую емкость и наоборот.
Объяснение: некоторые материалы меньше сопротивляются интенсивности поля при любом заданном напряжении, а следовательно, накапливают больший заряд.
Относительная диэлектрическая проницаемость характеризует проницаемость материала в сравнении с чистым вакуумом. Чем больше число, тем больше диэлектрическая проницаемость материала. Относительная диэлектрическая проницаемость стекла, например, в семь раз выше относительной диэлектрической проницаемости вакуума. Это позволяет создать интенсивность поля в семь раз большую, чем у вакуума, при прочих равных условиях.
Ниже приведена таблица относительной диэлектрической проницаемости наиболее распространенных материалов:
| Материал | Относительная диэлектрическая проницаемость | ||
| Вакуум | 1,0000 | ||
| Воздух | 1,0006 | ||
| Тефлон | 2,0 | ||
| Полипропилен | 2,20 — 2,28 | ||
| Каучук | 2,4 | ||
| Полистирол | 2,45 — 4,0 | ||
| Вощеная бумага | 2,5 | ||
| Трансформаторное масло | 2,5 — 4,0 | ||
| Жесткая резина | 2,5 — 4,8 | ||
| Дерево (дуб) | 3,3 | ||
| Силикон | 3,4 — 4,3 | ||
| Бакелит | 3,5 — 6,0 | ||
| Кварц | 3,8 | ||
| Дерево (клен) | 4,4 | ||
| Стекло | 4,9 — 7,5 | ||
| Касторовое масло | 5,0 | ||
| Дерево (береза) | 5,2 | ||
| Слюда | 5,0 — 8,7 | ||
| Фарфор | 6,5 | ||
| Оксид алюминия, глинозем | 8,0 — 10,0 | ||
| Дистиллированная вода | 80,0 | ||
| Барий-стронций титанит | 7500 | ||
Приблизительная емкость для любой пары разделенных проводников может быть найдена с помощью следующей формулы:
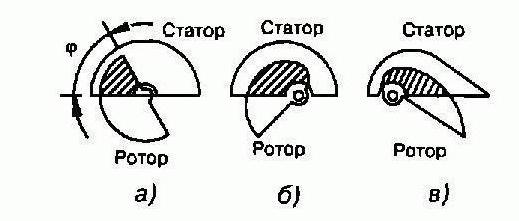
Конденсатор можно сделать переменным, если изменяемым будет любой из факторов, влияющих на его емкость. Наиболее легко изменяемым фактором является площадь пластин.
Следующие фотографии показывают пример переменного конденсатора, который состоит из набора чередующихся металлических пластин, и использующий воздушный зазор в качестве диэлектрического материала:
Емкость конденсаторов: определение, формулы, примеры.
Определение 1Конденсатор – это совокупность двух любых проводников, заряды которых одинаковы по значению и противоположны по знаку.
Его конфигурация говорит о том, что поле, созданное зарядами, локализовано между обкладками. Тогда можно записать формулу электроемкости конденсатора:
C=qφ1-φ2=qU.
Значением φ1-φ2=U обозначают разность потенциалов, называемую напряжением, то есть U. По определению емкость положительна. Она зависит только от размерностей обкладок конденсатора их взаиморасположения и диэлектрика. Ее форма и место должны минимизировать воздействие внешнего поля на внутреннее. Силовые линии конденсатора начинаются на проводнике с положительным зарядом, а заканчиваются с отрицательным. Конденсатор может являться проводником, помещенным в полость, окруженным замкнутой оболочкой.
Выделяют три большие группы: плоские, сферические, цилиндрические. Чтобы найти емкость, необходимо обратиться к определению напряжения конденсатора с известными значениями зарядов на обкладках.
Плоский конденсатор
Определение 2Плоский конденсатор – это две противоположно заряженные пластины, которые разделены тонким слоем диэлектрика, как показано на рисунке 1.
Формула для расчета электроемкости записывается как
C=εε0Sd, где S является площадью обкладки, d – расстоянием между ними, ε — диэлектрической проницаемостью вещества. Меньшее значение d способствует большему совпадению расчетной емкости конденсатора с реальной.
Рисунок 1
При известной электроемкости конденсатора, заполненного N слоями диэлектрика, толщина слоя с номером i равняется di, вычисление диэлектрической проницаемости этого слоя εi выполняется, исходя из формулы:
C=ε0Sd1ε1+d2ε2+…+dNεN.
Сферический конденсатор
Определение 3Когда проводник имеет форму шара или сферы, тогда внешняя замкнутая оболочка является концентрической сферой, э
Конденсатор
Конденсатор состоит из двух пластин (или обкладок), находящихся одна перед другой и сделанных из проводящего материала. Между пластинами находится изолирующий материал, называемый диэлектриком (рис. 4.1). Простейшими диэлектриками являются воздух, бумага, слюда и т. д.
Рис. 4.1. Конденсатор
Зарядка конденсатора
Основным свойством конденсатора является его способность запасать электрическую энергию в виде электрического заряда.
На рис. 4.2(а) изображена схема, в которой конденсатор соединяется через ключ с источником питания. Когда ключ замкнут (рис. 4.2(б)), положительный полюс источника «откачивает» электроны с обкладки А, и она приобретает положительный заряд. Отрицательный полюс источника питания тем временем «поставляет» электроны на обкладку В, в результате чего она приобретает отрицательный заряд, по абсолютной величине равный положительному заряду обкладки А. Такой поток электронов называется током заряда. Он продолжает течь до тех пор, пока напряжение на конденсаторе не сравняется с ЭДС источника питания. В этом случае говорят, что конденсатор полностью заряжен. Электрический заряд обозначается буквой Q, а его величина измеряется в кулонах (Кл).
Рис. 4.2. Заряд и разряд конденсатора
Когда конденсатор заряжен, между его обкладками возникает разность потенциалов, а следовательно, и электрическое поле.
Если в момент, когда конденсатор уже зарядился, разомкнуть ключ (рис. 4.2(в)), конденсатор будет хранить заряд. В этом случае внутри диэлектрика между обкладками возникает электрическое поле. При разряде конденсатора через сопротивление нагрузки (рис. 4.2(г)) электрическое ноле исчезает.
Емкость конденсатора
Способность конденсатора накапливать электрический заряд называется емкостью, а величина этой емкости обозначается буквой С и измеряется в фарадах (Ф). Фарада — очень большая единица емкости, и поэтому она практически не используется. Чаще используются дробные единицы:
1 микрофарада (мкФ) = Ф = 10-6 Ф,
1 пикофарада (пФ) = мкФ = 10-6 мкФ = 10-12 Ф.
Емкость конденсатора возрастает с увеличением площади обкладок и убывает с увеличением расстояния между ними.
Например, при возрастании площади обкладок вдвое емкость также увеличивается в два раза. Если же увеличить вдвое расстояние между обкладками, емкость станет вдвое меньше.
Связь заряда, емкости и напряжения
Если конденсатор заряжен до разности потенциалов V , его заряд определяется формулой Q=CV
где С выражается в фарадах, V – в вольтах, а Q – в кулонах. Преобразовав эту формулу, получим:
Энергия заряженного конденсатора
Энергия W, запасенная конденсатором, определяется формулой
где W выражается в джоулях, С – в фарадах, а V — в вольтах.
Параллельное и последовательное соединение конденсаторов
Если два конденсатора, С1 и С2, соединены параллельно (рис. 4.3(а)), результирующая емкость СТ такого соединения равна сумме емкостей этих конденсаторов:
Если конденсаторы соединены последовательно (рис. 4.3(б)), результирующая емкость СТ оказывается меньше емкости любого из конденсаторов я выражается формулой
Например, если С1 = С2, то результирующая емкость СТ последовательного соединения равна половине емкости любого из конденсаторов:
Напряжение на последовательно соединенных конденсаторах
На схеме, показанной на рис. 4.4, конденсаторы С1 и С2 соединены последовательно и подключены к источнику постоянного напряжения VТ. Полное напряжение VТ будет поделено между С1 и С2 таким образом, что на конденсаторе меньшей емкости установится большее напряжение,
Рис. 4.3. Параллельное (а) и последовательное (б) соединение конденсаторов.
Рис. 4.4. Напряжение на конденсаторах при их последовательном соединении
и наоборот.
Сумма V1 (напряжения на С1) и V2 (напряжения на С2) всегда равна полному напряжению VТ.
В общем случае, когда несколько конденсаторов, соединенных последовательно, подключено к источнику постоянного тока, напряжение на каждом из конденсаторов обратно пропорционально его емкости. При последовательном соединении двух конденсаторов напряжения на С1 и С2 соответственно равны
Пример 1
Определим результирующую емкость цепи, изображенной на рис. 4.5. Результирующая емкость параллельного соединения равна
С2 + С3 = 10 + 20 = 30 пФ
Поскольку емкость С1 также равна 30 пФ, то результирующая емкость всей цепи равна ½*30 = 15 пФ.
Рис. 4.6. Рис. 4.7.
Пример 2
На рис. 4.6 напряжение на конденсаторе С1 равно
откуда напряжение на С2 равно 30 – 20 = 10 В.
Рабочее напряжение
Любой конденсатор характеризуется некоторым максимальным напряжением, при превышении которого наступает пробой диэлектрика. Это напряжение называется рабочим, или номинальным, напряжением конденсатора, и подаваемое на конденсатор напряжение ни в коем случае не должно его превышать. При использовании конденсатора в цепях переменного тока амплитудное значение напряжения в цепи также не должно превышать рабочего напряжения конденсатора. Рабочим напряжением для батареи конденсаторов, соединенных параллельно, является наименьшее из рабочих напряжений конденсаторов, входящих в схему, Например, рабочее напряжение для цепи, изображенной на рис. 4.7, равно 25 В.
Для конденсаторов, соединенных последовательно, рабочее напряжение подбирать труднее. Рассмотрим схему на рис. 4.8. Конденсатор С1 (1 мкФ, рабочее напряжение Vраб = 25 В) соединен последовательно с конденсатором С2 (10 мкФ, Vраб = 10 В). Поскольку на конденсаторе С1, обладающем меньшей емкостью, установится большее напряжение, чем на С2, то при расчетах следует прежде всего иметь в виду рабочее напряжение конденсатора С1, равное 25 В. Таким образом, V1 = 25 В. соотношения V1/ V2 = С1/ С2 следует, что
Поскольку рабочее напряжение конденсатора С2 выше, чем V2, рабочее напряжение данной батареи конденсаторов равно 25 + 2,5 = 27,5 В.
Следует заметить, что если бы рабочее напряжение конденсатора было равно, например, 2 В, как показано на рис. 4.9, то он зарядился бы
Рис. 4.8. Рис. 4.9.
Рис. 4.10. Рис. 4.11. Катушка индуктивности
до уровня рабочего напряжения прежде, чем напряжение на конденсаторе С1 достигло бы 25 В. Вот расчет для этого случая:
V2 = 2 В, тогда.
Следовательно, рабочее напряжение такой батареи будет составлять 20 + 2 = 22 В.
Пример 3
Конденсаторы С1 и С2, изображенные на рис. 4.10, имеют каждый рабочее напряжение 60 В. Какое максимальное напряжение может быть приложено к этой схеме?
Решение
Поскольку на конденсаторе С1 установится более высокое напряжение, чем на конденсаторе С2, то напряжение на нем раньше достигнет уровня рабочего напряжения. При V1 = 60 В
Максимальное напряжение, которое может быть подано на данную схему, составляет 60 + 20 = 80 В.
В этом видео рассказывается о понятии конденсатора:
Добавить комментарий
Устройство конденсатора его назначение, характеристики и параметры
Конденсаторы
Конденсатор – электронный компонент, предназначенный для накопления электрического заряда. Способность конденсатора накапливать электрический заряд зависит от его главной характеристики – емкости. Емкость конденсатора (С) определяется как соотношение количества электрического заряда (Q) к напряжению (U).
Емкость конденсатора измеряется в фарадах (F) – единицах, названых в честь британского ученого физика Майкла Фарадея. Емкость в один фарад (1F) равняется количеству заряда в один кулон (1C), создающему напряжение на конденсаторе в один вольт (1V). Вспомним, что один кулон (1С) равняется величине заряда, прошедшего через проводник за одну секунду (1 sec) при силе тока в один ампер (1A).
Однако кулон, это очень большое количество заряда относительно того, сколько способно хранить большинство конденсаторов. По этой причине, для измерения емкости обычно используют микрофарады (µF или uF), нанофарады (nF) и пикофарады (pF).
- 1µF = 0.000001 = 10-6 F
- 1nF = 0.000000001 = 10-9 F
- 1pF = 0.000000000001 = 10-12 F
Плоский конденсатор
Существует множество типов конденсаторов различной формы и внутреннего устройства. Рассмотрим самый простой и принципиальный — плоский конденсатор. Плоский конденсатор состоит из двух параллельных пластин проводника (обкладок), электрически изолированных друг от друга воздухом, или специальным диэлектрическим материалом (например бумага, стекло или слюда).
Устройство конденсатора
Заряд конденсатора. Ток
По своему предназначению конденсатор напоминает батарейку, однако все же он сильно отличается по принципу работы, максимальной емкости, а также скорости зарядки/разрядки.
Рассмотрим принцип работы плоского конденсатора. Если подключить к нему источник питания, на одной пластине проводника начнут собираться отрицательно заряженные частицы в виде электронов, на другой – положительно заряженные частицы в виде ионов. Поскольку между обкладками находиться диэлектрик, заряженные частицы не могут «перескочить» на противоположную сторону конденсатора. Тем не менее, электроны передвигаются от источника питания — до пластины конденсатора. Поэтому в цепи идет электрический ток.
В самом начале включения конденсатора в цепь, на его обкладках больше всего свободного места. Следовательно, начальный ток в этот момент встречает меньше всего сопротивления и является максимальным. По мере заполнения конденсатора заряженными частицами ток постепенно падает, пока не закончится свободное место на обкладках и ток совсем не прекратится.
Время между состояниями «пустого» конденсатора с максимальным значением тока, и «полного» конденсатора с минимальным значением тока (т.е. его отсутствием), называют переходным периодом заряда конденсатора.
Напряжение между обкладками
В самом начале переходного периода зарядки, напряжение между обкладками конденсатора равняется нулю. Как только на обкладках начинают появляться заряженные частицы, между разноименными зарядами возникает напряжение. Причиной этому является диэлектрик между пластинами, который «мешает» стремящимся друг к другу зарядам с противоположным знаком перейти на другую сторону конденсатора.
На начальном этапе зарядки, напряжение быстро растет, потому что большой ток очень быстро увеличивает количество заряженных частиц на обкладках. Чем больше заряжается конденсатор, тем меньше ток, и тeм медленнее растет напряжение. В конце переходного периода, напряжение на конденсаторе полностью прекратит рост, и будет равняться напряжению на источнике питания.
Как видно на графике, сила тока конденсатора напрямую зависит от изменения напряжения.
Формула для нахождения тока конденсатора во время переходного периода:
- Ic — ток конденсатора
- C — Емкость конденсатора
- Vc/t – Изменение напряжения на конденсаторе за отрезок времени
Разряд конденсатора
После того как конденсатор зарядился, отключим источник питания и подключим нагрузку R. Так как конденсатор уже заряжен, он сам превратился в источник питания. Нагрузка R образовала проход между пластинами. Отрицательно заряженные электроны, накопленные на одной пластине, согласно силе притяжения между разноименными зарядами, двинутся в сторону положительно заряженных ионов на другой пластине.
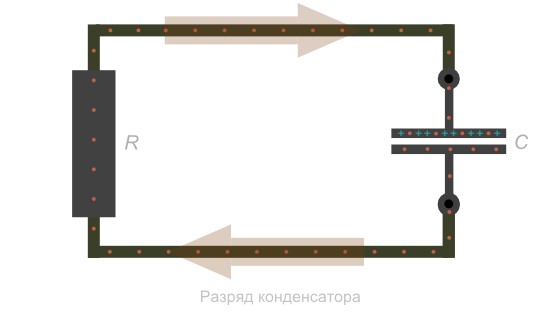
В момент подключения R, напряжение на конденсаторе то же, что и после окончания переходного периода зарядки. Начальный ток по закону Ома будет равняться напряжению на обкладках, разделенном на сопротивление нагрузки.
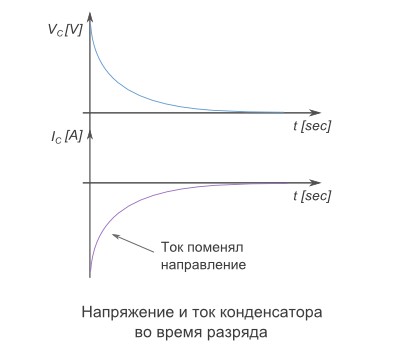
Как только в цепи пойдет ток, конденсатор начнет разряжаться. По мере потери заряда, напряжение начнет падать. Следовательно, ток тоже упадет. По мере понижения значений напряжения и тока, будет снижаться их скорость падения.
Время зарядки и разрядки конденсатора зависит от двух параметров – емкости конденсатора C и общего сопротивления в цепи R. Чем больше емкость конденсатора, тем большее количество заряда должно пройти по цепи, и тем больше времени потребует процесс зарядки/разрядки ( ток определяется как количество заряда, прошедшего по проводнику за единицу времени). Чем больше сопротивление R, тем меньше ток. Соответственно, больше времени потребуется на зарядку.
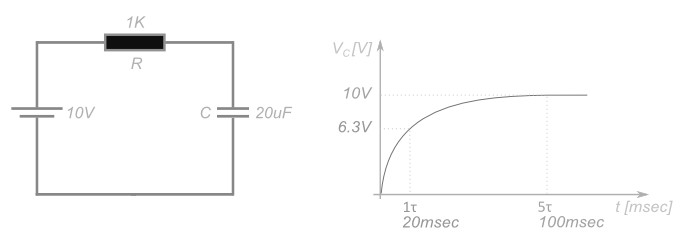
Продукт RC (сопротивление, умноженное на емкость) формирует временную константу ? (тау). За один ? конденсатор заряжается или разряжается на 63%. За пять ? конденсатор заряжается или разряжается полностью.
Для наглядности подставим значения: конденсатор емкостью в 20 микрофарад, сопротивление в 1 килоом и источник питания в 10В. Процесс заряда будет выглядеть следующим образом:
Устройство конденсатора. От чего зависит емкость
Емкость плоского конденсатора зависит от трех основных факторов:
- Площадь пластин — A
- Расстояние между пластинами – d
- Относительная диэлектрическая проницаемость вещества между пластинами — ?
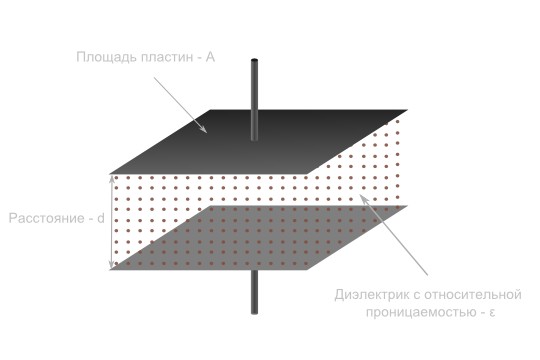
Площадь пластин
Чем больше площадь пластин конденсатора, тем больше заряженных частиц могут на них разместится, и тем больше емкость.
Расстояние между пластинами
Емкость конденсатора обратно пропорциональна расстоянию между пластинами. Для того чтобы объяснить природу влияния этого фактора, необходимо вспомнить механику взаимодействия зарядов в пространстве (электростатику).
Если конденсатор не находится в электрической цепи, то на заряженные частицы, расположенные на его пластинах влияют две силы. Первая — это сила отталкивания между одноименными зарядами соседних частиц на одной пластине. Вторая – это сила притяжения разноименных зарядов между частицами, находящимися на противоположных пластинах. Получается, что чем ближе друг к другу находятся пластины, тем больше суммарная сила притяжения зарядов с противоположным знаком, и тем больше заряда может разместится на одной пластине.
Относительная диэлектрическая проницаемость
Не менее значимым фактором, влияющим на емкость конденсатора, является такое свойство материала между обкладками как относительная диэлектрическая проницаемость. Это безразмерная физическая величина, которая показывает во сколько раз сила взаимодействия двух свободных зарядов в диэлектрике меньше, чем в вакууме.
Материалы с более высокой диэлектрической проницаемостью позволяют обеспечить большую емкость. Объясняется это эффектом поляризации – смещением электронов атомов диэлектрика в сторону положительно заряженной пластины конденсатора.
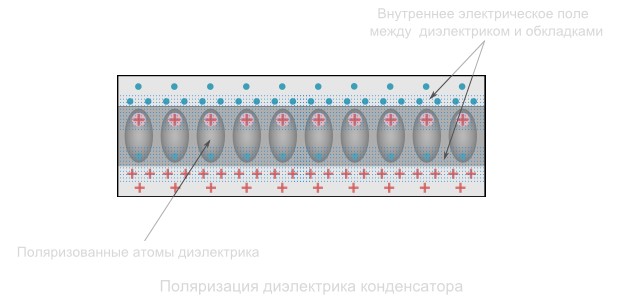
Поляризация создает внутренне электрическое поле диэлектрика, которое ослабляет общую разность потенциала (напряжения) конденсатора. Напряжение U препятствует притоку заряда Q на конденсатор. Следовательно, понижение напряжения способствует размещению на конденсаторе большего количества электрического заряда.
Ниже приведены примеры значений диэлектрической проницаемости для некоторых изоляционных материалов, используемых в конденсаторах.
- Бумага – от 2.5 до 3.5
- Стекло – от 3 до 10
- Слюда – от 5 до 7
- Порошки оксидов металлов – от 6 до 20
Номинальное напряжение
Второй по значимости характеристикой после емкости является максимальное номинальное напряжение конденсатора. Данный параметр обозначает максимальное напряжение, которое может выдержать конденсатор. Превышение этого значения приводит к «пробиванию» изолятора между пластинами и короткому замыканию. Номинальное напряжение зависит от материала изолятора и его толщины (расстояния между обкладками).
Следует отметить, что при работе с переменным напряжением нужно учитывать именно пиковое значение (наибольшее мгновенное значение напряжения за период). Например, если эффективное напряжение источника питания будет 50В, то его пиковое значение будет свыше 70В. Соответственно необходимо использовать конденсатор с номинальным напряжением более 70В. Однако на практике, рекомендуется использовать конденсатор с номинальным напряжением не менее в два раза превышающим максимально возможное напряжение, которое будет к нему приложено.
Ток утечки
Также при работе конденсатора учитывается такой параметр как ток утечки. Поскольку в реальной жизни диэлектрик между пластинами все же пропускает маленький ток, это приводит к потере со временем начального заряда конденсатора.
Для чего нужен конденсатор и как он работает
Конденсатор (от латинского слова «condensare» — «уплотнять», «сгущать») — это двухполюсное устройство с определённой величиной или переменным значением ёмкости и малой проводимостью, которое способно сосредотачивать, накапливать и отдавать другим элементам электрической цепи заряд электрического тока.
Конденсатор или как его еще называют сокращенно просто «кондер» — это элемент электрической цепи, состоящий в самом простом варианте из двух электродов в форме пластин (или обкладок), которые накапливают противоположные разряды и поэтому они разделены между собой диэлектриком малой толщины по сравнению с размерами самих электропроводящих обкладок.На практике же, все выпускаемые конденсаторы представляют собой многослойные рулоны лент электродов в форме цилиндра или параллелепипеда, разделенных между собой слоями диэлектрика.
Принцип работы конденсатора
По принципу работы он схож с батарейкой только на первый взгляд, но все же он сильно отличается от него по принципу и скорости заряда-разряда, максимальной емкости.
Заряд конденсатора. В момент подключения к источнику питания оказывается больше всего места на электродах, поэтому и ток будет зарядки максимальным, но по мере накопления заряда, ток будет уменьшаться и пропадет полностью после полного заряда. При зарядке на одной пластине будут собираться отрицательно заряженные частицы- электроны, а на другой – ионы, положительно заряженные частицы. Диэлектрик выступает препятствием для их перескакивания на противоположную сторону конденсатора.При зарядке растет и напряжение с нуля перед началом зарядки и достигает в самом конце максимума, равного напряжению источника питания.
Разрядка конденсатора. Если после окончания зарядки отключить источник питания и подключить нагрузку R, то он сам превратится в источник тока. При подключении нагрузки образовывается цепь между пластинами. Отрицательно заряженные электроны двинуться через нагрузку к положительно заряженных ионам на другой пластине по закону притяжения между разноименными зарядами.В момент подключения нагрузки, начальный ток по закону Ома будет равняться величине напряжения на электродах (равного в конце зарядке конденсатора напряжению источника питания), разделенному на сопротивление нагрузки.
После того как пошел ток, конденсатор начинает постепенно терять заряд или разряжаться. Одновременно с этим начнет снижаться величина напряжения, соответственно по закону Ома и ток. В то же время чем выше уровень разряда обкладок, тем ниже будет скорость падения напряжения и силы тока. Процесс завершится после того, как напряжение на электродах конденсатора станет равно нулю.
Время зарядки конденсатора на прямую зависит от величины его емкости. Чем большей она величины, тем дольше будет проходить по цепи большее количество заряда.
Время разрядки зависит от величины подключенной нагрузки. Чем больше подключено сопротивление R, тем меньше будет ток разрядки.
Для чего нужен конденсатор
Конденсаторы широко используются во всех электронных и радиотехнических схемах. Они вместе с транзисторами и резисторами являются основой радиотехники.
Применение конденсаторов в электротехнических устройствах и бытовой технике:
- Важным свойством конденсатора в цепи переменного тока является его способность выступать в роли емкостного сопротивления (индуктивное у катушки). Если подключить последовательно конденсатор и лампочку к батарейке, то она не будет светиться. Но если подключить к источнику переменного тока, то она загорится. И светиться будет тем ярче, чем выше емкость конденсатора. Благодаря этому свойству они широко применяются в качестве фильтра, который способен довольно успешно подавлять ВЧ и НЧ помехи, пульсации напряжения и скачки переменного тока.
- Благодаря способности конденсаторов долгое время накапливать заряд и затем быстро разряжаться в цепи с малым сопротивлением для создания импульса, делает их незаменимыми при производстве фотовспышек, ускорителей электромагнитного типа, лазеров и т. п.
- Способность конденсатора накапливать и сохранять электрический заряд на продолжительное время, сделало возможным использование его в элементах для сохранения информации. А так же в качестве источника питания для маломощных устройств. Например, пробника электрика, который достаточно вставить в розетку на пару секунд пока не зарядится в нем встроенный конденсатор и затем можно целый день прозванивать цепи с его помощью. Но к сожалению, конденсатор значительно уступает в способности накапливать электроэнергию аккумуляторной батареи из-за токов утечки (саморазряда) и неспособности накопить электроэнергию большой величины.
- Конденсаторы используются при подключении электродвигателя 380 на 220 Вольт. Он подключается к третьему выводу, и благодаря тому что он сдвигает фазу на 90 градусов на третьем выводе- становится возможным использования трехфазного мотора в однофазной сети 220 Вольт.
- В промышленности конденсаторные установки применяются для компенсации реактивной энергии.
В следующей статье мы рассмотрим подробно основные характеристики и типы конденсаторов.
Что такое емкость конденсатора? :: SYL.ru
Конденсатор является одной из самых важных частей любой мало-мальски сложной схемы. Наибольшую ценность для нас представляет его емкость. Что это такое? Как она измеряется? Какие есть нюансы? Эти, а также и другие вопросы будут рассмотрены в рамках статьи.
Это название характеристики проводника, которая обозначает возможность накопления электрического заряда. В теории электрических цепей так называют взаимную ёмкость, существующую между двумя разными проводниками. Она определяется как соотношение размера заряда к разности потенциалов между ними.Измерение емкости
Международная система единиц для обозначения использует фарады, а СГС – сантиметры. Одиночный проводник имеет ёмкость, которая равна отношению заряда к потенциалу. При этом считается, что все другие подобные устройства находятся на бесконечном расстоянии и что их потенциал равен нулю.
Что такое конденсатор?
Это двухполюсник, обладающий переменным или определенным значением ёмкости и малой проводимостью. Данное устройство может копить заряд и энергию электрического поля. Конденсатор относится к пассивным электронным компонентам. Его примитивная конструкция может иметь два электрода, выполненных в форме пластин, которые разделены диэлектриком. Последний имеет малую толщину (если сравнивать его с обкладками). Но на практике широкое распространение нашли устройства, которые обладают многослойными диэлектриками и электродами. Они могут быть выполнены в виде ленты, где чередуются обе части, или сворачиваются в параллелепипед, у которого скруглены четыре ребра, или цилиндр.Ёмкость
Давайте более детально рассмотрим этот параметр. Напомню, что он характеризирует возможность накапливания конденсатором электрического заряда. На приборы всегда наносят номинальную ёмкость. А вот реальная может сильно варьироваться в зависимости от многих факторов. Данный показатель говорит о реальных электрических свойствах. Он может быть размером как в несколько единиц пикофарад, так и в тысячи микрофарад. Отдельный класс конденсаторов (ионисторы) могут похвастаться значениями вообще в несколько фарад. Отдельного внимания заслуживает каждый тип, но в конце будет рассмотрен только плоский как пример реализации. Чтобы получить большую емкость, чем есть в наличных конденсаторах, их соединяют параллельно. Напряжение между обкладками у них всегда одинаковое. Чтобы получить ёмкость батареи, необходимо просуммировать характеристики каждого из конденсаторов. Если устройства, расположенные параллельно, имеют ещё и одинаковое расстояние между своими обкладками, и их диэлектрики действуют по одному принципу, то они все рассматриваются как одно целое. Для достижения одинаковых зарядов необходимо устройства соединять последовательно. В таких случаях емкость будет всегда меньше, чем у конденсатора с минимальным значением. Но и возможность пробоя значительно уменьшается благодаря тому, что на одно устройство приходится только часть потенциала источника напряжения. При одинаковой площади обкладок все конденсаторы представляются в виде одного большого прибора.Удельная ёмкость
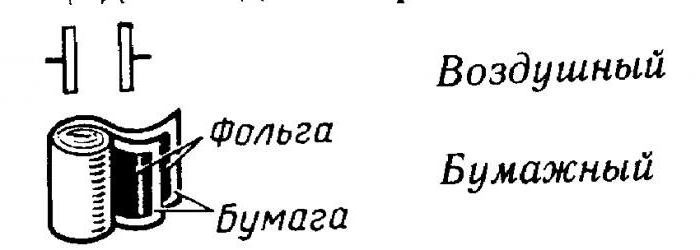Это соотношение ёмкости к массе или объему диэлектрика. Чем он тоньше, тем выше будет показатель. Негативной стороной повышения удельной ёмкости является то, что возрастают риски пробоя.Плотность энергии
Она зависит от особенностей конструктивного исполнения электролитического конденсатора. Максимальная плотность бывает исключительно у больших конденсаторов. Это возможно благодаря тому, что масса корпуса является небольшой сравнительно с весом электролита и обкладок.
Давайте рассмотрим конденсатор EPCOS B4345. Он обладает емкостью в 12 000 мкФ. Максимально допустимое напряжение составляет 450 В. А общая масса равняется 1 килограмму и 900 граммам! При этом плотность энергии достигает показателя в 639 (845) Дж/кг (Дж/л). Где же могут найти себе применение конденсаторы с такими характеристиками? Иметь параметры указанного размера нужно там, где устройство необходимо использовать как накопитель энергии, чтобы в последующем резко её освободить. Пример использования – пушка Гаусса.
Емкость плоского конденсатора
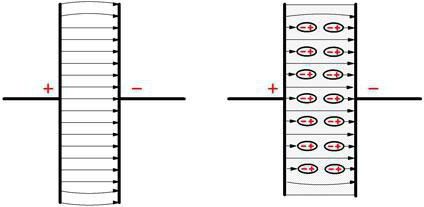Как и было обещано ранее, сейчас рассмотрим пример. Для начала давайте ознакомимся с одной небольшой формулой:ЕПК=ДП*ЭП*П/Р, где
- ЕПК – емкость плоского конденсатора.
- ДП – диэлектрическая проницаемость среды, которая заполняет пространство, находящееся между пластинами. В вакууме этот показатель равен единице.
- Р – расстояние между пластинами конденсатора.
- ЭП – электрическая постоянная. Численно она равна 8,854187817·10−12 Ф/м (справедливо в случаях, когда Р значительно меньше линейного размера пластин).
- П – площадь металлической пластины, которая расположена в конденсаторе.
Давайте подведём итог уравнения. Из преведенной выше формулы можно сделать заключение, что емкость у плоских конденсатором напрямую зависит от размера устройства, его формы, а также диэлектрической проницаемости. Учтобы создать прибор с большей характеристикой, необходимо будет сделать два действия:
- уменьшить толщину слоя диэлектрика в устройстве;
- увеличить площадь пластин, которые используются в конденсаторе.
Опасность разрушения
Взрывом электролитического конденсатора опытного практика удивить сложно. В качестве причины выхода из строя чаще всего называют перегрев устройства, который происходит из-за утечки или увеличения последовательного эквивалентного сопротивления. В повседневной жизни часто с таким встречаются владельцы компьютеров, у которых конденсаторы находятся около источников повышенного тепловыделения (в роли которых часто выступают радиаторы охлаждения). Чтобы избежать повреждения других деталей, а также травматизма, во многих моделях имеется вышибной предохранительный клапан. Также может быть нанесена насечка корпуса. Когда происходит повышение внутреннего давления, то пробой совершается, как правило, в помеченном месте. Это из-за того, что вырваться в данной точке энергии значительно легче. При этом обычно обходится без взрыва.
Применение на практике
Какую особенность имеет емкость конденсатора на практике? Она необходима в случаях, когда необходимо выбросить значительное количество энергии. В видимом для нас спектре их практическое применение обычно является незаметным. Но всё же можно убедится, что всё именно так. Примером этого являются случаи, когда емкость конденсатора используется в рельсотронах или других подобных устройствах. Главное в них – высвободить за доли секунд значительные объемы энергии, которые при этом будут двигаться в направлении, указанном человеком.Заключение
Вот и закончен обзор ёмкости конденсатора – самого важного параметра данного устройства. Чем большая ёмкость конденсатора используется, тем осторожнее требуется работать с ним на практике. Так, старые устройства, которые изготавливались в герметичных оболочках, при внезапном выходе из строя могут нанести значительные повреждения человеку. Подобные замечания можно высказать и относительно дешевых конденсаторов, которые привозят к нам из Китая.
Изменение ёмкости керамических конденсаторов от температуры и напряжения, или как ваш конденсатор на 4,7мкФ превращается в 0,33мкФ
Вступление: я был озадачен.
Несколько лет назад, после более чем 25 лет работы с этими вещами, я узнал кое-что новое о керамических конденсаторах. Работая над драйвером светодиодной лампы я обнаружил, что постоянная времени RC-цепочки в моей схеме не сильно смахивает на расчётную.
Предположив, что на плату были впаяны не те компоненты, я измерил сопротивление двух резисторов составлявших делитель напряжения — они были весьма точны. Тогда был выпаян конденсатор — он так же был великолепен. Просто чтобы убедиться, я взял новые резисторы и конденсатор, измерил их, и впаял обратно. После этого я включил схему, проверил основные показатели, и ожидал увидеть что моя проблема с RC-цепочкой решена… Если бы.
Я проверял схему в её естественной среде: в корпусе, который в свою очередь сам по себе был зачехлён чтобы имитировать кожух потолочного светильника. Температура компонентов в некоторых местах достигала более чем 100ºC. Для уверенности, и чтобы освежить память я перечитал даташит на используемые конденсаторы. Так началось моё переосмысление керамических конденсаторов.
Справочная информация об основных типах керамических конденсаторов.
Для тех кто этого не помнит (как практически все), в таблице 1 указана маркировка основных типов конденсаторов и её значение. Эта таблица описывает конденсаторы второго и третьего класса. Не вдаваясь глубоко в подробности, конденсаторы первого класса обычно сделаны на диэлектрике типа C0G (NP0).
Таблица 1.
| Нижняя рабочая температура | Верхняя рабочая температура | Изменение ёмкости в диапазоне (макс.) | |||
|---|---|---|---|---|---|
| Символ | Температура (ºC) | Символ | Температура (ºC) | Символ | Изменение (%) |
| Z | +10 | 2 | +45 | A | ±1.0 |
| Y | -30 | 4 | +65 | B | ±1.5 |
| X | -55 | 5 | +85 | C | ±2.2 |
| – | – | 6 | +105 | D | ±3.3 |
| – | – | 7 | +125 | E | ±4.7 |
| – | – | 8 | +150 | F | ±7.5 |
| – | – | 9 | +200 | P | ±10 |
| – | – | – | – | R | ±15 |
| – | – | – | – | S | ±22 |
| – | – | – | – | T | +22, -33 |
| – | – | – | – | U | +22, -56 |
| – | – | – | – | V | +22, -82 |
Из описанных выше на моём жизненном пути чаще всего мне попадались конденсаторы типа X5R, X7R и Y5V. Я никогда не использовал конденсаторы типа Y5V из-за их экстремально высокой чувствительности к внешним воздействиям.
Когда производитель конденсаторов разрабатывает новый продукт, он подбирает диэлектрик так, чтобы ёмкость конденсатора изменялась не более определённых пределов в определённом температурном диапазоне. Конденсаторы X7R которые я использую не должны изменять свою ёмкость более чем на ±15% (третий символ) при изменении температуры от -55ºC (первый символ) до +125ºC (второй символ). Так что, либо мне попалась плохая партия, либо что-то ещё происходит в моей схеме.
Не все X7R созданы одинаковыми.
Так как изменение постоянной времени моей RC-цепочки было куда больше, чем это могло быть объяснено температурным коэффициентом ёмкости, мне пришлось копать глубже. Глядя на то, насколько уплыла ёмкость моего конденсатора от приложенного к нему напряжения я был очень удивлён. Результат был очень далёк от того номинала, который был впаян. Я брал конденсатор на 16В для работы в цепи 12В. Даташит говорил, что мои 4,7мкФ превращаются в 1,5мкФ в таких условиях. Это объясняло мою проблему.
Даташит также говорил, что если только увеличить типоразмер с 0805 до 1206, то результирующая ёмкость в тех же условиях будет уже 3,4мкФ! Этот момент требовал более пристального изучения.
Я нашёл, что сайты Murata® и TDK® имеют классные инструменты для построения графиков изменения ёмкости конденсаторов в зависимости от различных условий. Я прогнал через них керамические конденсаторы на 4,7мкФ для разных типоразмеров и номинальных напряжений. На рисунке 1 показаны графики построенные Murata. Были взяты конденсаторы X5R и X7R типоразмеров от 0603 до 1812 на напряжение от 6,3 до 25В.
Рисунок 1. Изменение ёмкости в зависимости от приложенного напряжения для выбранных конденсаторов.
Обратите внимание, что во-первых, при увеличении типоразмера уменьшается изменение ёмкости в зависимости от приложенного напряжения, и наоборот.
Второй интересный момент состоит в том, что в отличии от типа диэлектрика и типоразмера, номинальное напряжение похоже ни на что не влияет. Я ожидал бы, что конденсатор на 25В под напряжением 12В меньше изменит свою ёмкость, чем конденсатор на 16В под тем же напряжением. Глядя на график для X5R типоразмера 1206 мы видим, что конденсатор на 6,3В на самом деле ведёт себя лучше, чем его родня на большее номинальное напряжение.
Если взять более широкий ряд конденсаторов, то мы увидим, что это поведение характерно для всех керамических конденсаторов в целом.
Третье наблюдение состоит в том, что X7R при том же типоразмере имеет меньшую чувствительность к изменениям напряжения, чем X5R. Не знаю, насколько универсально это правило, но в моём случае это так.
Используя данные графиков, составим таблицу 2, показывающую насколько уменьшится ёмкость конденсаторов X7R при 12В.
Таблица 2. Уменьшение ёмкости конденсаторов X7R разных типоразмеров при напряжении 12В.
| Типоразмер | Ёмкость, мкФ | % от номинала |
|---|---|---|
| 0805 | 1,53 | 32,6 |
| 1206 | 3,43 | 73,0 |
| 1210 | 4,16 | 88,5 |
| 1812 | 4,18 | 88,9 |
| Номинал | 4,7 | 100 |
Мы видим устойчивое улучшение ситуации по мере роста размера корпуса пока мы не достигнем типоразмера 1210. Дальнейшее увеличение корпуса уже не имеет смысла.
В моём случае я выбрал наименьший возможный типоразмер компонентов, поскольку этот параметр был критичен для моего проекта. В своём невежестве я полагал что любой конденсатор X7R будет так же хорошо работать, как другой с тем же диэлектриком — и был неправ. Чтобы RC-цепочка заработала правильно я должен был взять конденсатор того же номинала, но в большем корпусе.
Выбор правильного конденсатора
Я очень не хотел использовать конденсатор типоразмера 1210. К счастью, я имел возможность увеличить сопротивление резисторов в пять раз, уменьшив при этом ёмкость до 1мкФ. Графики на рисунке 2 показывают поведение различных X7R конденсаторов 1мкФ на 16В в сравнении с их собратьями X7R 4,7мкФ на 16В.
Рисунок 2. Поведение различных конденсаторов на 1мкФ и 4,7мкФ.
Конденсатор 0603 1мкФ ведёт себя так же, как 0805 4,7мкФ. Вместе взятые 0805 и 1206 на 1мкФ чувствуют себя лучше, чем 4,7мкФ типоразмера 1210. Используя конденсатор 1мкФ в корпусе 0805 я мог сохранить требования к размерам компонентов, получив при этом в рабочем режиме 85% от исходной ёмкости, а не 30%, как было ранее.
Но это ещё не всё. Я был изрядно озадачен, ибо считал что все конденсаторы X7R должны иметь сходные коэффициенты изменения ёмкости от напряжения, поскольку все выполены на одном и том же диэлектрике — а именно X7R. Я связался с коллегой — специалистом по керамическим конденсаторам1. Он пояснил, что есть много материалов, которые квалифицируются как «X7R». На самом деле, любой материал который позволяет компоненту функционировать в температурном диапазоне от -55ºC до +125ºC с изменением характеристик не более чем на ±15% можно назвать «X7R». Так же он сказал, что нет каких-либо спецификаций на коэффициент изменения ёмкости от напряжения ни для X7R, ни для каких-либо других типов.
Это очень важный момент, и я его повторю. Производитель может называть конденсатор X7R (или X5R, или еще как-нибудь) до тех пор, пока он соответствует допускам по температурному коэффициенту ёмкости. Вне зависимости от того, насколько плох его коэффициент по напряжению.
Для инженера-разработчика этот факт только освежает старую шутку — «любой опытный инженер знает: читай даташит!»
Производители выпускают всё более миниатюрные компоненты, и вынуждены искать компромиссные материалы. Для того чтобы обеспечить необходимые ёмкостно-габаритные показатели, им приходится ухудшать коэффициенты по напряжению. Конечно, более авторитетные производители делают все возможное, чтобы свести к минимуму неблагоприятные последствия этого компромисса.
А как насчёт типа Y5V, который я сразу отбросил? Для контрольного в голову, давайте рассмотрим обычный конденсатор Y5V. Я не буду выделять какого-то конкретного производителя этих конденсаторов — все примерно одинаковы. Выберем 4,7мкФ на 6,3В в корпусе 0603, и посмотрим его параметры при температуре +85ºC и напряжении 5В. Типовая ёмкость на 92,3% ниже номинала, или 0,33мкФ. Это так. Приложив 5В к этому конденсатору мы получаем падение ёмкости в 14 раз по сравнению с номиналом.
При температуре +85ºC и напряжении 0В ёмкость уменьшается на 68,14%, с 4,7мкФ до 1,5мкФ. Можно предположить, что приложив 5В мы получим дальнейшее уменьшение ёмкости — от 0,33мкФ до 0,11мкФ. К счастью, эти эффекты не объединяются. Уменьшение ёмкости под напряжением 5В при комнатной температуре куда хуже, чем при +85ºC.
Для ясности, в данном случае при напряжении 0В ёмкость падает от 4,7мкФ до 1,5мкФ при +85ºC, в то время как при напряжении 5В ёмкость конденсатора увеличивается от 0,33мкФ при комнатной температуре, до 0,39мкФ при +85ºC. Это должно убедить вас действительно тщательно проверять все спецификации тех компонентов, которые вы используете.
Вывод
В результате этого урока я уже не просто указываю типы X7R или X5R коллегам или поставщикам. Вместо этого я указываю конкретные партии конкретных поставщиков, которые я сам проверил. Я также предупреждаю клиентов о том, чтобы они перепроверяли спецификации при рассмотрении альтернативных поставщиков для производства, чтобы гарантировать что они не столкнутся с этими проблемами.
Главный вывод из всей этой истории, как вы наверное догадались, это: «читайте даташиты!». Всегда. Без исключений. Запросите дополнительные данные, если даташит не содержит достаточной информации. Помните, что обозначения керамических конденсаторов X7V, Y5V и т.д. совершенно ничего не говорят о их коэффициентах по напряжению. Инженеры должны перепроверять данные чтобы знать, реально знать о том, как используемые конденсаторы будут вести себя в реальных условиях. В общем, имейте в виду, в нашей безумной гонке за меньшими и меньшими габаритами это становится всё более важным моментом каждый день.
Об авторе
Марк Фортунато провёл большую часть жизни пытаясь сделать так, чтобы эти противные электроны оказались в нужное время в нужном месте. Он работал над различными вещами — от систем распознавания речи и микроволновой аппаратуры, до светодиодных ламп (тех, которые регулируются правильно, заметьте!). Он провёл последние 16 лет помогая клиентам приручить их аналоговые схемы. Г-н Фортунато сейчас является ведущим специалистом подразделения коммуникационных и автомобильных решений Maxim Integrated. Когда он не пасёт электроны, Марк любит тренировать молодёжь, читать публицистику, смотреть как его младший сын играет в лакросс, а старший сын играет музыку. В целом, он стремится жить в гармонии. Марк очень сожалеет, что больше не встретится с Джимом Уильямсом или Бобом Пизом.
Сноски
1 Автор хотел бы поблагодарить Криса Буркетта, инженера по применению из TDK за его объяснения «что здесь, чёрт возьми, происходит».
Murata является зарегистрированной торговой маркой компании Murata Manufacturing Co., Ltd.
TDK является зарегистрированным знаком обслуживания и зарегистрированной торговой маркой корпорации TDK.
P.S. По просьбам трудящихся — сравнительное фото конденсаторов различных типоразмеров. Шаг сетки 5мм.