Уравнение состояния идеального газа. Базовый уровень 10 класс онлайн-подготовка на Ростелеком Лицей
Связь трех параметров состояния идеального газа. Уравнение Менделеева – Клапейрона
Состояние газа однозначно задается тремя макроскопическими параметрами: давлением, объемом и температурой. Мы знаем, что горячий воздух поднимается вверх. С увеличением температуры он становится легче – уменьшается плотность, увеличивается расстояние между молекулами. То есть происходит расширение – увеличение объема. Можно сделать вывод, что объем и температура газа связаны. Если сдавить воздушный шарик, то внутри него увеличится давление. То есть объем газа также связан с давлением. Получается, что давление, объем и температура газа связаны между собой. Попробуем понять, как именно.
Мы работаем с моделью идеального газа, которая описывает реальный газ достаточно точно для решения многих задач. Мы уже получили для идеального газа основное уравнение МКТ, с помощью которого связали давление с микропараметрами – массой и средней скоростью одной молекулы:
Это уравнение – решение задачи в модели механики.
Мы приняли, что газ состоит из хаотично движущихся молекул – и вычислили, как они действуют на стенку, какое давление создают, когда с ней сталкиваются. Но мы не измеряем скорости и массы отдельных молекул. На макроуровне мы умеем измерять температуру, которую мы связали со средней кинетической энергией молекул, а значит, и с микропараметрами: массой и средней скоростью одной молекулы:
Подставив кинетическую энергию из одного уравнения в другое, получили:
В таком виде применять уравнение для решения задач все еще не удобно. Для измерения давления газа существуют различные приборы (манометры, барометры), для измерения температуры – термометры. Но мы не можем напрямую измерять концентрацию – количество частиц в единице объема. Преобразуем уравнение до удобного вида. Концентрация – это, по определению, :
А количество молекул удобнее представить через количество вещества. Мы помним, что в одном моле вещества молекул. Значит, :
Договоримся: чтобы каждый раз не перемножать постоянные величины на , сделаем это один раз, а произведение обозначим :
Это значение назвали универсальной газовой постоянной, почему – станет понятно чуть позже.
Умножим обе части уравнения на объем и перепишем:
Получили уравнение, которое связывает три макропараметра идеального газа, которые легко измерить: объем, температуру и давление. И если взять какое-то определенное количество газа , эти три параметра однозначно зададут его состояние, неизвестных в уравнении не останется. Поэтому это уравнение назвали уравнением состояния идеального газа, или иначе уравнением Менделеева – Клапейрона. А на случай, если нам неудобно пользоваться количеством вещества в молях, можно его выразить через массу вещества:
Именно в этом виде его чаще всего и записывают. Мы начали с движения молекул, придумали инструменты для его описания, а в итоге получили уравнение, которое связывает поддающиеся непосредственному измерению макропараметры.
Решим задачу.
Задача 1. Какое давление должен выдерживать газовый баллон объемом 50 л, чтобы при температуре 25 ˚С в нем можно было хранить 2 кг метана ()?
Анализ условия.
В задаче сказано о метане – это газ, в баллоне не создается экстремальных условий, температура комнатная, так что будем описывать его с помощью модели идеального газа. Речь идет о связи трех макропараметров газа, поэтому будем применять уравнение состояния идеального газа.
Физическая часть решения. В условии задана масса газа, поэтому запишем уравнение состояния идеального газа в том виде, в котором есть масса:
Все величины известны, осталось только найти молярную массу метана (ее можно найти, зная состав его молекулы, см. рис. 1), перевести значения величин в СИ и получить ответ. На выборе уравнения физика закончилась, осталось решить простое уравнение. Выразим давление:
Рис. 1. Углерод и водород в таблице Менделеева
Молекула метана состоит из одного атома углерода с относительной атомной массой 12 (смотрим в таблице Менделеева) и четырех атомов водорода с относительной атомной массой 1. Тогда:
Будем использовать в СИ:
1 л – это 1 или в СИ .
Значит, объем баллона в СИ будет равен .
Температуру выразим в кельвинах:
Вычислим давление:
Получили ответ: давление около 6,2 МПа, что в 62 раза больше атмосферного. Задача решена.
Во многих задачах берется некоторое фиксированное количество газа и рассматривается изменение его состояния. Это значит, что в рамках таких задач количество вещества постоянно (как и масса, смотря в чем выразим). Можно все постоянные перенести в одну часть уравнения, а три изменяющихся параметра состояния – в другую:
или
Если взять 1 моль любого газа (одноатомного аргона, углекислого газа, водяного пара – лишь бы к нему была применима модель идеального газа), выражение будет равно постоянной . Поэтому эта постоянная и названа универсальной. Но даже если мы возьмем произвольную, но – что важно – фиксированную массу газа, выражение для этой массы газа будет постоянным:
Или, по-другому, если газ переходит из одного состояния с параметрами , , в состояние с параметрами , , , то можем записать:
В таком виде или в виде это уравнение называют уравнением Клапейрона, хотя это то же уравнение состояния, записанное немного иначе.
Газовые законы
Рассматривать изменение переменной от двух других не очень удобно. У нас есть подходящий математический инструмент для описания одной переменной от другой – функция. В рассмотренных в начале урока примерах мы фиксировали один из трех параметров газа (например, температуру) и рассматривали зависимость двух других. Подробно рассмотрим все три случая.
Начнем с фиксированной температуры и рассмотрим связь давления и объема в этом случае. Процессы, в которых мы считаем неизменным один из параметров состояния газа, назвали изопроцессами, от древнегреческого ἴσος, что означает «одинаковый, равный». А процесс, в котором сохраняется температура (const), называется изотермическим (несложно запомнить: термос – то, что сохраняет температуру).
Умножим обе части уравнения Клапейрона на температуру:
Если умножить постоянную температуру на константу, то получим тоже константу, только другую:
Нам даже не нужно знать ее значение, главное, что произведение p на V каким было в начале процесса, таким и осталось в конце:
Из уравнения видно: при уменьшении объема (сжатии) при постоянной температуре увеличивается давление, и наоборот (на математике мы говорили, что такая зависимость называется обратной пропорциональностью).
Мы получили это уравнение, воспользовавшись математической моделью, но еще в XVII веке эту закономерность экспериментально выявили англичанин Бойль и француз Мариотт, поэтому ее назвали в их честь законом Бойля – Мариотта:
Для газа данной массы при постоянной температуре произведение давления газа на его объем постоянно.
Как это выглядит на практике? Представьте шар с мягкой резиновой оболочкой или цилиндр со скользящим поршнем, в которых находится определенная масса газа. Как добиться того, чтобы при сжатии газа его температура оставалась постоянной? Газ должен обмениваться теплотой с большим телом с неизменной температурой – термостатом (см. рис. 2).
Рис. 2. Сжатие газа, отвод теплоты для постоянной температуры
Реально ли поддерживать таким способом постоянную температуру? Нет, для этого газ нужно сжимать очень медленно, чтобы он успевал остывать, едва начиная нагреваться. Но если не будет разности температур, то и теплообмена не будет: тепло передается от теплого холодному.
Поэтому процесс сможет протекать так: небольшими шагами сжимаем газ, чтобы на каждом таком шаге он немного нагревался и это тепло тут же забирал термостат. Постоянная температура – это приближение, тем не менее достаточно точно описывающее реальный процесс и позволяющее решать задачи.
Зафиксируем второй параметр – давление, при этом меняться будут температура и объем. Давление мы ассоциируем с древнегреческим βαρύς – «тяжелый», вы знаете, что атмосферное давление измеряют барометром, поэтому процесс с постоянным давлением (onst) назвали изобарным.
Разделим обе части уравнения Клапейрона на давление:
Если разделить константу на постоянное давление, то получим тоже константу:
А если рассмотреть объем и температуру в начале и в конце изобарного процесса, можно записать:
Из уравнения видно: при увеличении температуры (нагревании) при постоянном давлении увеличивается объем (газ расширяется), и наоборот, при охлаждении – сжимается. Это пример прямой пропорциональности.
До того как вывели этот закон математически, его экспериментально получил Гей-Люссак (это двойная фамилия одного человека, французского ученого), поэтому его назвали законом Гей-Люссака:
Для данной массы газа при постоянном давлении отношение объема к температуре постоянно.
Пример реального процесса, который можно описывать как изобарный: газ, который находится в цилиндре под поршнем, который свободно перемещается и на который снаружи действует постоянное давление, например атмосферное. Тогда, если нагреть этот газ, он будет расширяться, но давление как было равным атмосферному (плюс давление самого поршня), так и останется.
На самом деле, если давление газа совсем не будет увеличиваться, у поршня не будет причин двигаться, давления будут все время уравновешены. Так что давление немного увеличивается, но под его действием поршень сдвигается вверх, и оно тут же понижается до прежнего значения. Эти изменения небольшие, так что для решения многих задач давление можно действительно считать постоянным.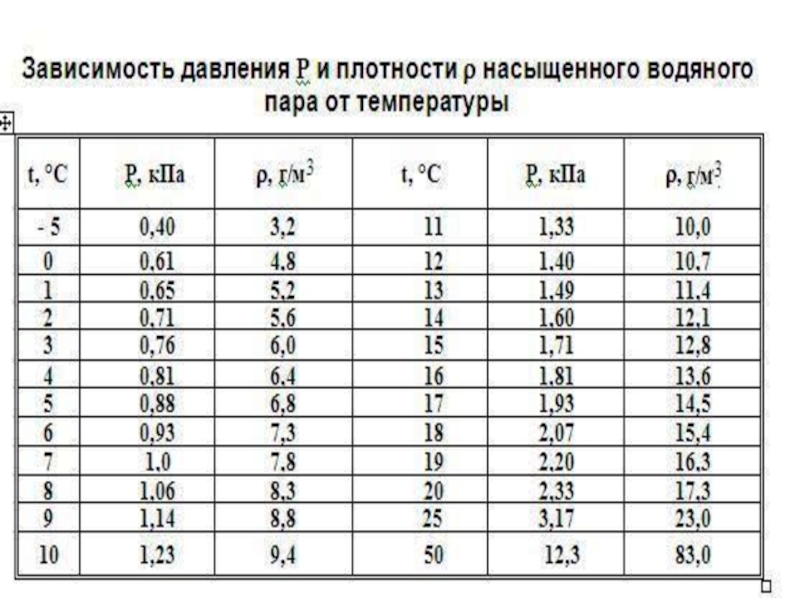
И остался третий параметр, который мы еще не фиксировали, – объем, при этом изменяются температура и давление. Называется такой процесс, при котором (onst), изохорным, от древнегреческого χῶρος – «место, пространство». Разделим обе части уравнения Клапейрона на объем:
Справа получилась константа:
Теперь можно связать давление и температуру в начале и в конце изохорного процесса:
Из уравнения видно: при увеличении температуры (нагревании) при постоянном объеме увеличивается давление газа, и наоборот. Это тоже прямая пропорциональность. И этот закон тоже сначала был получен экспериментально, французским ученым Шарлем, поэтому и назван его именем – закон Шарля:
Для газа данной массы отношение давления к температуре постоянно, если объем не меняется.
Для этого процесса модель точнее описывает реальный процесс: в закрытом жестком сосуде объем действительно можно считать постоянным с хорошей точностью. Пример – металлический баллон.
Если газ в нем нагреть, давление увеличится, но при большой жесткости баллона он практически не деформируется (по крайне мере настолько, чтобы внести заметную погрешность в расчеты).
Решение задач. Графики для описания газовых законов. Границы применимости модели
Итак, какие инструменты мы получили? Основной инструмент один – уравнение состояния идеального газа. А все остальное – это запись этого же уравнения в более удобных формах для решения той или иной задачи. Если мы имеем дело с неизменной массой газа (то есть нет утечек), то три параметра состояния связаны уравнением Клапейрона. А если при этом еще и остается неизменным один из параметров состояния, применяем уравнение для изотермического, изобарного или изохорного процесса, их еще называют газовыми законами. Применим наши инструменты, решив несколько задач.
Задача 2. При сжатии воздуха в цилиндре дизельного двигателя объем воздуха уменьшается в 15 раз, а температура повышается от 47 до 620 ˚С.
Каково давление воздуха в конце сжатия, если в начале сжатия давление воздуха было равно атмосферному (100 кПа)?
Анализ условия.
Физическая часть решения. Запишем уравнение в виде, удобном для описания перехода из состояния 1 в состояние 2:
Температуры заданы (нужно только перевести их в кельвины), давление тоже. Что сказано об объеме – перепишем условие в математическом виде. Объем уменьшился в 15 раз, это значит, что в состоянии 2 объем в 15 раз меньше, чем в состоянии 1:
Получили простую систему уравнений, решим ее – это будет математическая часть решения.
Выразим давление во втором состоянии:
Получили ответ: 4,2 МПа (или 42 атмосферы).
Задача 3. После повышения температуры на 15 К давление газа в закрытом баллоне увеличилось на 3 %. Какой была начальная температура?
Анализ условия. В задаче описано изменение состояния газа. За неимением другой информации будем применять модель идеального газа. Речь идет о закрытом баллоне. Это значит, во-первых, что масса газа постоянна, а, во-вторых, баллоны обычно жесткие, значит, и объем не изменяется. Поэтому можем описать процесс как изохорный.
Физическая часть решения. Запишем уравнение для изохорного процесса:
Перепишем условие в математическом виде, чтобы можно было подставлять в уравнение. Температура увеличилась на 15 К, значит,.
А давление увеличилось на 3 %, это по-другому можно записать:
Физика здесь закончилась на выборе закона, которым описывать процесс, осталось подставить переписанные величины и решить уравнение:
Нашли начальную температуру, она равна 500 К.
Или, в более привычных для нас градусах Цельсия, 227 ˚С.
Часто бывает удобно выразить зависимость одного параметра от другого в виде графиков. Это наглядно, помогает лучше представить себе процесс, а иногда по графикам можно оценить численные значения. Начертим графики зависимостей параметров газа и разберемся, какую информацию можно из них получить. Начнем с изотермического процесса, .
Чтобы начертить график зависимости давления от объема, нужно переписать уравнение в виде :
Это обратно пропорциональная зависимость типа , и ее график имеет вид гиперболы (см. рис. 3).
Рис. 3. Изотермический процесс на графике зависимости давления от температуры
От константы зависит расположение кривой: чем больше константа, тем выше располагается график. А вы помните, что константа содержит температуру, в промежуточном варианте уравнение выглядело так:
Так что если у нас есть две изотермы для одной и той же массы газа, значит, каждая изотерма описывает процесс, при котором температура постоянна.
Но в первом случае эта постоянная температура равна , которая меньше, чем постоянная температура во втором случае (см. рис. 3).
Графики двух остальных изопроцессов мы будем рассматривать в координатах и , поэтому сразу рассмотрим и изотермический процесс в этих координатах. Начертим график (см. рис. 4) изотермы в координатах .
Рис. 4. Изотермический процесс на графике зависимости
Температура не меняется, значит, графики будут перпендикулярны оси Т, а объем при этой температуре приобретает разные значения. И легко определить по оси
Аналогично выглядят графики изотермического процесса в координатах : температура постоянна, температура для второго процесса больше, чем для первого. А давление изменяется при изменении объема, которого на графике явно не видно, но можно понять по изменению давления (см.
рис. 5).
Рис. 5. Изотермический процесс на графике зависимости
Теперь рассмотрим изобарный процесс.
Представим в виде зависимости :
Это прямо пропорциональная зависимость вида , ее график – прямая, которая начинается в точке начала координат (см. рис. 6).
Рис. 6. График зависимости для изобарного процесса
Коэффициентом перед определяется крутизна графика. Там у нас стоит константа, которая содержит давление, вспомните промежуточное уравнение, полученное из уравнения Клапейрона:
Там давление в числителе, поэтому чем больше давление, тем меньше коэффициент пропорциональности на графике и тем ниже располагается график. Поэтому у двух процессов, происходящих с одной и той же массой газа при разных давлениях: .
Рис. 7. График зависимости для двух изобарных процессов при разных давлениях
Начертим графики изобары в двух других системах координат. В координатах найдем на оси нужное нам давление и горизонтальной прямой покажем, что при любом изменении объема оно не изменяется.
При другом давлении это будет такая же прямая, только выше или ниже (см. рис. 8).
Рис. 8. Графики зависимости и для изобарного процесса
И последним рассмотрим изохорный процесс:
Представим в виде зависимости :
Это тоже прямо пропорциональная зависимость вида , с графиком – прямой, крутизна которой определяется коэффициентом перед переменной , а в нашем случае – .
Рис. 9. График зависимости для изохорного процесса
Этот коэффициент определяется объемом, при котором протекает изохорный процесс, и чем объем меньше, тем коэффициент больше и график круче:
Графики, описывающие изохорные процессы при разных объемах, в координатах и , начертите самостоятельно. И напоследок поговорим о границах применимости моделей.
Мы подробно обсудили, что в реальности нельзя абсолютно точно сохранять неизменными температуру, давление или объем при изопроцессах.
Но реальный газ нельзя, например, охлаждать до сколь угодно малых температур, чтобы он сжимался до сколь угодно малого объема. В какой-то момент размеры молекул не будут уже пренебрежимо малыми по сравнению с расстояниями между ними, а это уже не описывается моделью идеального газа. Усилится взаимодействие между молекулами, которым мы изначально пренебрегли, и газ перейдет в состояние жидкости (см. рис. 9).
Рис. 9. Границы применимости модели идеального газа
Конечно, это не значит, что физика здесь больше не работает. Если нужно рассмотреть состояние жидкости, это тоже можно сделать: у нее тоже можно измерить температуру, рассмотреть изменение объеме при сжатии – оно будет небольшим.
Список литературы
- Г.Я. Мякишев, Б.Б. Буховцев, Н.Н. Сотский. Физика 10. – М.: Просвещение, 2008.
- Касьянов В.А. Физика 10. – М.: Дрофа, 2000.
- М.М. Балашов, А.И. Гомонова, А.Б. Долицкий и др. Физика: Механика 10. – М.: Дрофа, 2004.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Интернет-портал Класс!ная физика
- Интернет-портал Класс!ная физика
Домашнее задание
- Начертите по памяти и объясните графики, описывающие изохорные процессы при разных объемах, в координатах и .
- До какой температуры нужно изобарически охладить некоторую массу газа с начальной температурой 40 ˚С, чтобы объем газа уменьшился при этом на одну четверть?
материалы для подготовки к ЕГЭ по Физике
Оглавление:
- Изотермический процесс
- Графики изотермического процесса
- Изобарный процесс
- Изохорный процесс
- Графики изохорного процесса
org/ListItem»> Темы кодификатора ЕГЭ: изопроцессы — изотермический, изохорный, изобарный процессы.Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ: изопроцессы — изотермический, изохорный, изобарный процессы.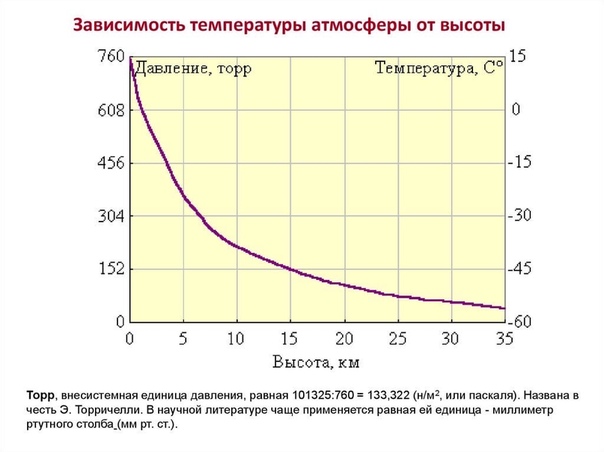
На протяжении этого листка мы будем придерживаться следующего предположения: масса и химический состав газа остаются неизменными. Иными словами, мы считаем, что:
• , то есть нет утечки газа из сосуда или, наоборот, притока газа в сосуд;
• , то есть частицы газа не испытывают каких-либо изменений (скажем, отсутствует диссоциация — распад молекул на атомы).
Эти два условия выполняются в очень многих физически интересных ситуациях (например, в простых моделях тепловых двигателей) и потому вполне заслуживают отдельного рассмотрения.
Если масса газа и его молярная масса фиксированы, то состояние газа определяется тремя макроскопическими параметрами: давлением, объёмом и температурой. Эти параметры связаны друг с другом уравнением состояния (уравнением Менделеева — Клапейрона).
Термодинамический процесс (или просто процесс) — это изменение состояния газа с течением времени. В ходе термодинамического процесса меняются значения макроскопических параметров — давления, объёма и температуры.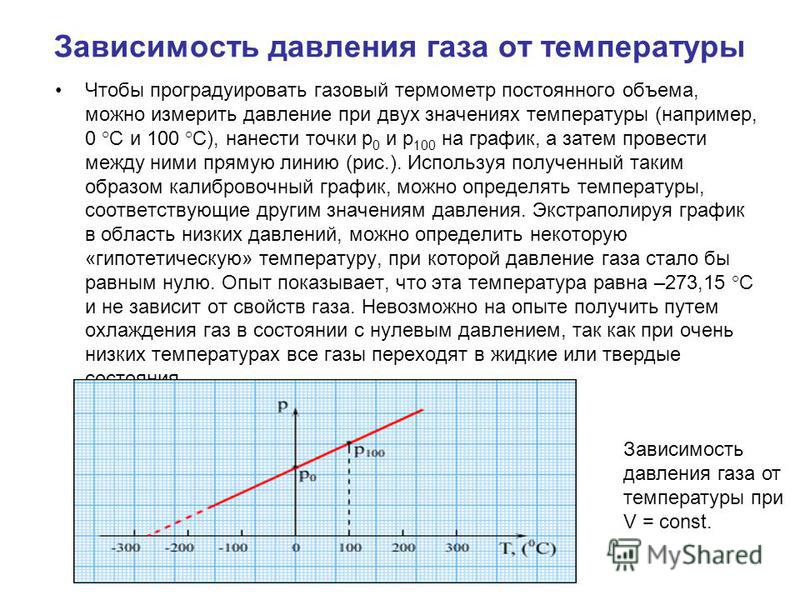
Особый интерес представляют изопроцессы — термодинамические процессы, в которых значение одного из макроскопических параметров остаётся неизменным. Поочерёдно фиксируя каждый из трёх параметров, мы получим три вида изопроцессов.
1. Изотермический процесс идёт при постоянной температуре газа: .
2. Изобарный процесс идёт при постоянном давлении газа: .
3. Изохорный процесс идёт при постоянном объёме газа: .
Изопроцессы описываются очень простыми законами Бойля — Мариотта, Гей-Люссака и Шарля. Давайте перейдём к их изучению.
Изотермический процесс
Пусть идеальный газ совершает изотермический процесс при температуре . В ходе процесса меняются только давление газа и его объём.
Рассмотрим два произвольных состояния газа: в одном из них значения макроскопических параметров равны , а во втором — . Эти значения связаны уравнением Менделеева-Клапейрона:
Как мы сказали с самого начала,масса и молярная масса предполагаются неизменными.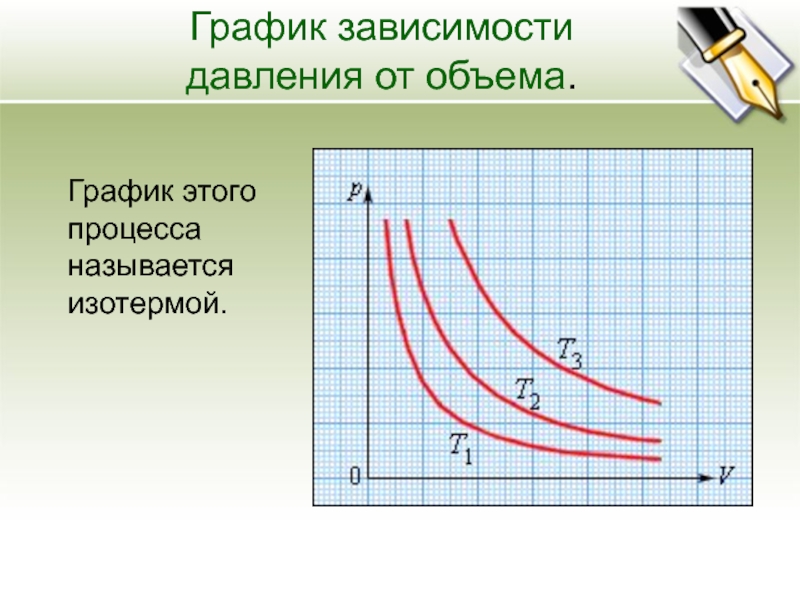
Поэтому правые части выписанных уравнений равны. Следовательно, равны и левые части:
(1)
Поскольку два состояния газа были выбраны произвольно, мы можем заключить, что в ходе изотермического процесса произведение давления газа на его объём остаётся постоянным:
(2)
Данное утверждение называется законом Бойля — Мариотта.
Записав закон Бойля — Мариотта в виде
(3)
можно дать и такую формулировку: в изотермическом процессе давление газа обратно пропорционально его объёму. Если, например, при изотермическом расширении газа его объём увеличивается в три раза, то давление газа при этом в три раза уменьшается.
Как объяснить обратную зависимость давления от объёма с физической точки зрения? При постоянной температуре остаётся неизменной средняя кинетическая энергия молекул газа, то есть, попросту говоря, не меняется сила ударов молекул о стенки сосуда. При увеличении объёма концентрация молекул уменьшается, и соответственно уменьшается число ударов молекул в единицу времени на единицу площади стенки — давление газа падает.
Наоборот, при уменьшении объёма концентрация молекул возрастает, их удары сыпятся чаще и давление газа увеличивается.
Графики изотермического процесса
Вообще, графики термодинамических процессов принято изображать в следующих системах координат:
• -диаграмма: ось абсцисс , ось ординат ;
• -диаграмма: ось абсцисс , ось ординат ;
• -диаграмма: ось абсцисс , ось ординат .
График изотермического процесса называется изотермой.
Изотерма на -диаграмме — это график обратно пропорциональной зависимости .
Такой график является гиперболой (вспомните алгебру — график функции ). Изотерма-гипербола изображена на рис. 1.
Рис. 1. Изотерма на -диаграмме
Каждая изотерма отвечает определённому фиксированному значению температуры. Оказывается, что чем выше температура, тем выше лежит соответствующая изотерма на —диаграмме.
В самом деле, рассмотрим два изотермических процесса, совершаемых одним и тем же газом (рис.
2). Первый процесс идёт при температуре , второй — при температуре .
Рис. 2. Чем выше температура, тем выше изотерма
Фиксируем некоторое значение объёма . На первой изотерме ему отвечает давление , на второй — . Но при фиксированном объёме давление тем больше, чем выше температура (молекулы начинают сильнее бить по стенкам). Значит, .
В оставшихся двух системах координат изотерма выглядит очень просто: это прямая, перпендикулярная оси (рис. 3):
Рис. 3. Изотермы на и -диаграммах
Изобарный процесс
Напомним ещё раз, что изобарный процесс — это процесс, проходящий при постоянном давлении. В ходе изобарного процесса меняются лишь объём газа и его температура.
Типичный пример изобарного процесса: газ находится под массивным поршнем, который может свободно перемещаться. Если масса поршня и поперечное сечение поршня , то давление газа всё время постоянно и равно
где — атмосферное давление.
Пусть идеальный газ совершает изобарный процесс при давлении . Снова рассмотрим два произвольных состояния газа; на этот раз значения макроскопических параметров будут равны и .
Выпишем уравнения состояния:
Поделив их друг на друга, получим:
В принципе, уже и этого могло бы быть достаточно, но мы пойдём немного дальше. Перепишем полученное соотношение так, чтобы в одной части фигурировали только параметры первого состояния, а в другой части — только параметры второго состояния (иными словами, «разнесём индексы» по разным частям):
(4)
А отсюда теперь — ввиду произвольности выбора состояний! — получаем закон Гей-Люссака:
(5)
Иными словами, при постоянном давлении газа его объём прямо пропорционален температуре:
(6)
Почему объём растёт с ростом температуры? При повышении температуры молекулы начинают бить сильнее и приподнимают поршень.
При этом концентрация молекул падает, удары становятся реже, так что в итоге давление сохраняет прежнее значение.
Графики изобарного процесса
График изобарного процесса называется изобарой. На -диаграмме изобара является прямой линией (рис. 4):
Рис. 4. Изобара на -диаграмме
Пунктирный участок графика означает, что в случае реального газа при достаточно низких температурах модель идеального газа (а вместе с ней и закон Гей-Люссака) перестаёт работать. В самом деле, при снижении температуры частицы газа двигаются всё медленнее, и силы межмолекулярного взаимодействия оказывают всё более существенное влияние на их движение (аналогия: медленный мяч легче поймать, чем быстрый). Ну а при совсем уж низких температурах газы и вовсе превращаются в жидкости.
Разберёмся теперь, как меняется положение изобары при изменении давления. Оказывается, что чем больше давление, тем ниже идёт изобара на —диаграмме.
Чтобы убедиться в этом, рассмотрим две изобары с давлениями и (рис. 5):
Рис. 5. Чем ниже изобара, тем больше давление
Зафиксируем некоторое значение температуры . Мы видим, что . Но при фиксированной температуре объём тем меньше, чем больше давление (закон Бойля — Мариотта!).
Стало быть, .
В оставшихся двух системах координат изобара является прямой линией, перпендикулярной оси (рис. 6):
Рис. 6. Изобары на и -диаграммах
Изохорный процесс
Изохорный процесс, напомним, — это процесс, проходящий при постоянном объёме. При изохорном процессе меняются только давление газа и его температура.
Изохорный процесс представить себе очень просто: это процесс, идущий в жёстком сосуде фиксированного объёма (или в цилиндре под поршнем, когда поршень закреплён).
Пусть идеальный газ совершает изохорный процесс в сосуде объёмом . Опять-таки рассмотрим два произвольных состояния газа с параметрами и .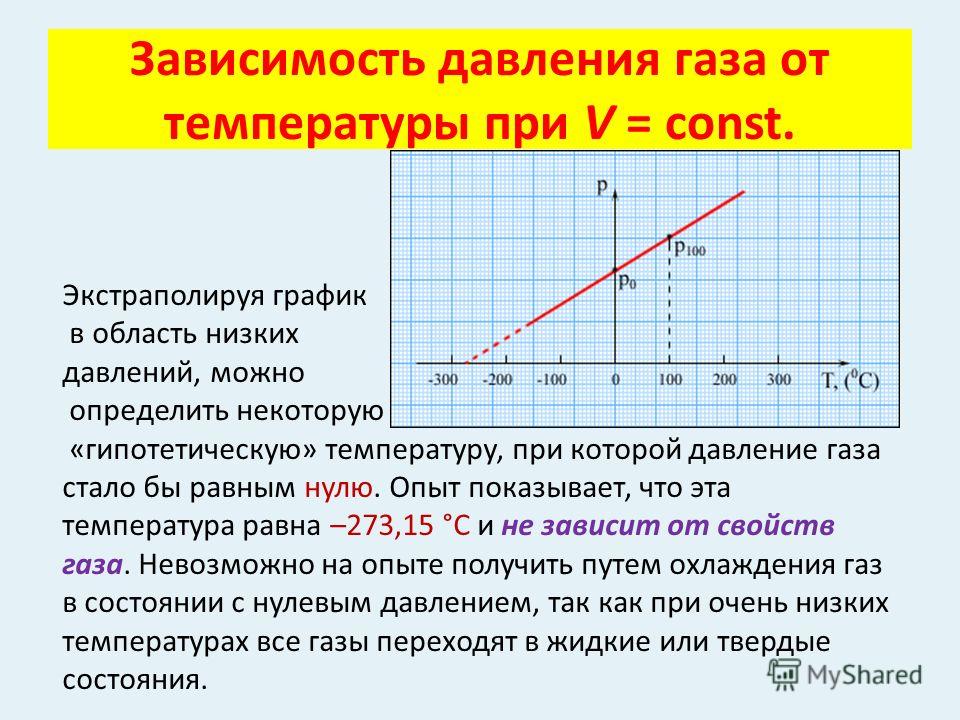
Имеем:
Делим эти уравнения друг на друга:
Как и при выводе закона Гей-Люссака, «разносим» индексы в разные части:
(7)
Ввиду произвольности выбора состояний мы приходим к закону Шарля:
(8)
Иными словами, при постоянном объёме газа его давление прямо пропорционально температуре:
(9)
Увеличение давления газа фиксированного объёма при его нагревании — вещь совершенно очевидная с физической точки зрения. Вы сами легко это объясните.
Графики изохорного процесса
График изохорного процесса называется изохорой. На -диаграмме изохора является прямой линией (рис. 7):
Рис. 7. Изохора на -диаграмме
Смысл пунктирного участка тот же: неадекватность модели идеального газа при низких температурах.
Далее, чем больше объём, тем ниже идёт изохора на —диаграмме (рис.
8):
Рис. 8. Чем ниже изохора, тем больше объём
Доказательство аналогично предыдущему. Фиксируем температуру и видим, что . Но при фиксированной температуре давление тем меньше, чем больше объём (снова закон Бойля — Мариотта). Стало быть, .
В оставшихся двух системах координат изохора является прямой линией, перпендикулярной оси (рис. 9):
Рис. 9. Изохоры на и -диаграммах
Законы Бойля — Мариотта, Гей-Люссака и Шарля называются также газовыми законами.
Мы вывели газовые законы из уравнения Менделеева — Клапейрона. Но исторически всё было наоборот: газовые законы были установлены экспериментально, и намного раньше. Уравнение состояния появилось впоследствии как их обобщение.
Благодарим за то, что пользуйтесь нашими публикациями.
Информация на странице «Изопроцессы» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.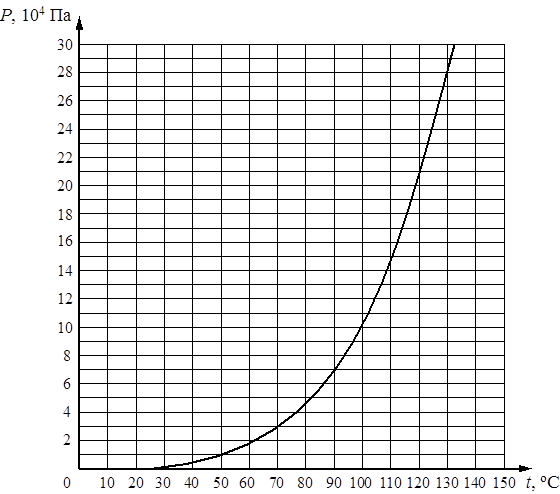
Чтобы успешно сдать нужные и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из данного раздела.
Публикация обновлена: 08.04.2023
Объяснение графиков давления и температуры— EngineerExcel
Часто использование графика или диаграммы может помочь упростить оценку взаимосвязи между параметрами вещества, такими как давление и температура. Два таких инструмента — график давления-температуры и диаграмма давления-температуры.
Содержание
- Диаграмма давления/температуры
- Критическая точка
- Тройная точка
- Фазовые линии
- Пример
- Зависимость давления от температуры для идеальных газов
- Пример расчета
- График давления-температуры для идеального газа
- Построение графика давления-температуры
- Использование графика давления-температуры 90 010
- Пример
Давление Температура Diagram
Другим полезным визуальным изображением, связывающим давление и температуру вещества, является диаграмма давление-температура.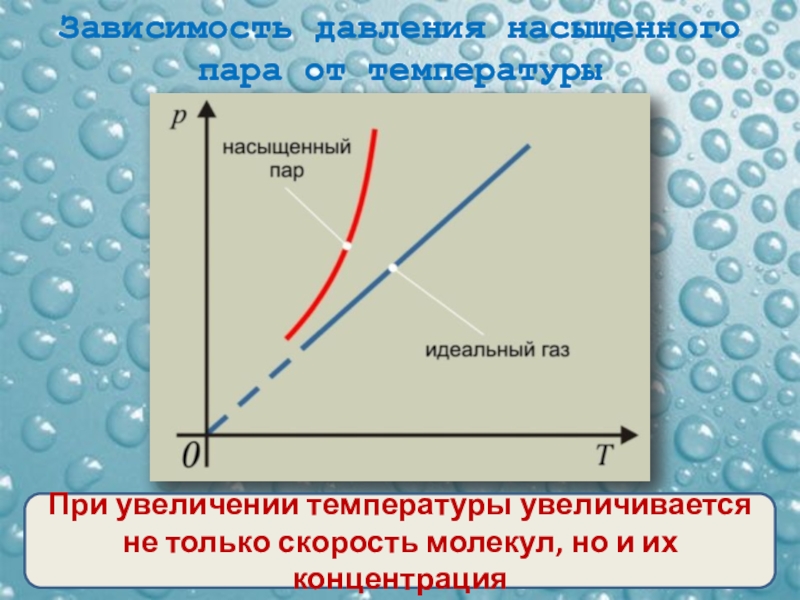
На этой диаграмме показаны фазы вещества (твердое, жидкое, парообразное) в зависимости от давления и температуры. Пример диаграммы давление-температура показан на следующем рисунке:
Для данного вещества изменения давления и температуры вызывают переход между фазами. На диаграмме давление-температура эти фазы отмечены вместе с парой других конкретных точек, критической точкой и тройной точкой.
Критическая точка
Критическая точка на диаграмме давления и температуры обозначает точку на линии между жидкой и паровой фазами, где повышение температуры больше не будет влиять на давление.
Тройная точка
Тройная точка обозначает удельное давление и температуру, при которых все три фазы вещества существуют одновременно. В этот момент данная молекула вещества может свободно переходить между тремя фазами.
Линии фаз
Линии между фазами, отмеченные на диаграмме давление-температура, указывают давление и температуру, при которых молекулы вещества, переходящие из одной фазы в другую (например, из жидкости в пар), равны молекулам, переходящим в другую пути (пар в жидкость).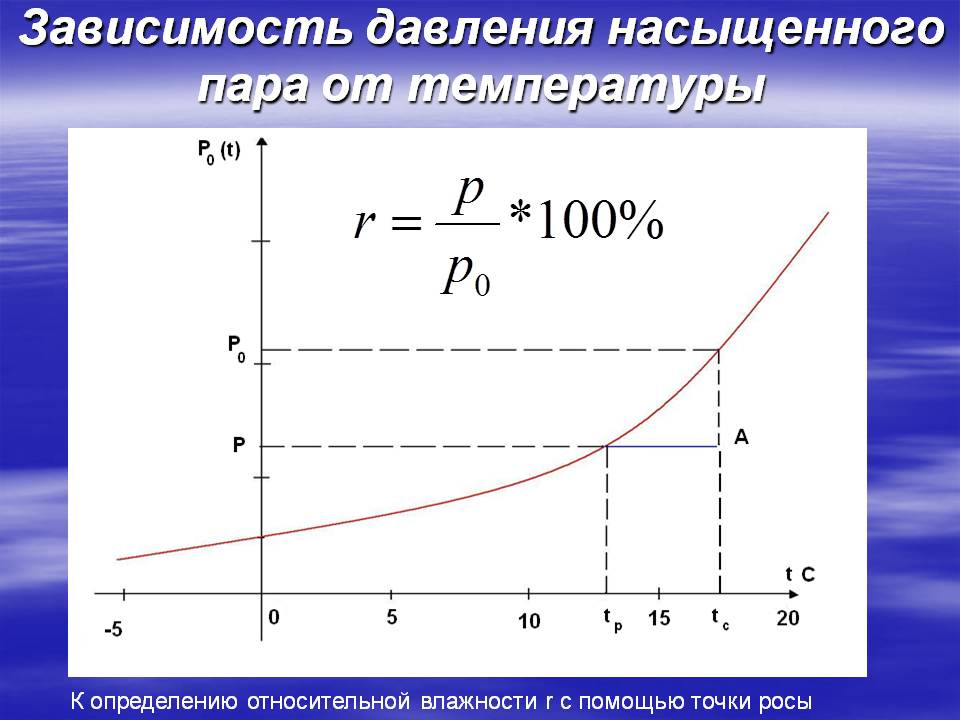
Пример
Используя диаграмму давление-температура, можно определить фазу вещества при заданных давлении и температуре. Для воды, диаграмма давления и температуры которой показана ниже, фаза при 105°F и 11 фунтов на квадратный фут представляет собой пар; фаза при 32°F и 47000 фунтов на квадратный фут является жидкой; фаза при 307°F и 31000 фунтов на квадратный фут является жидкой. Эти фазы демонстрируют, как различия в давлении и температуре влияют на фазу вещества.
Связь давления и температуры для идеальных газов
Связь между давлением и температурой определяется законом Гей-Люссака или законом Амонтона давления-температуры. Этот закон гласит, что давление фиксированной массы газа в фиксированном объеме будет увеличиваться с ростом температуры. Это отношение может быть выражено следующим уравнением:
где:
- P давление газа в фунтах/футах 2
- T – температура газа, выраженная в °F
- k – константа, отражающая массу газа и объем баллона
Преобразование приведенного выше уравнения дает следующее:
Используя взаимосвязь между давлением и температурой, можно связать и определить состояние газа в двух точках.
Пример расчета
В качестве примера оценки взаимосвязи между давлением и температурой для газа при давлении 100 фунтов/фут 2 при температуре 500°F, который нагревается до 750°F, конечное давление можно рассчитать следующим образом:
График давления-температуры для идеального газа
Для упрощения определения взаимосвязи между давлением и температурой для данного газа можно использовать график давления-температуры. Эти графики изображают линию с температурой по оси x и давлением по оси y . Ниже приведен пример графика давление-температура:
Построение графика давления-температуры
Данные, используемые для построения графика давления-температуры, получены путем экспериментов. Используя фиксированную массу определенного газа в фиксированном объеме, давление газа измеряется при различных температурах, и данные заносятся в таблицу, подобную приведенной ниже:
Эти отдельные точки данных наносятся друг на друга и рисуется линия, соединяющая их.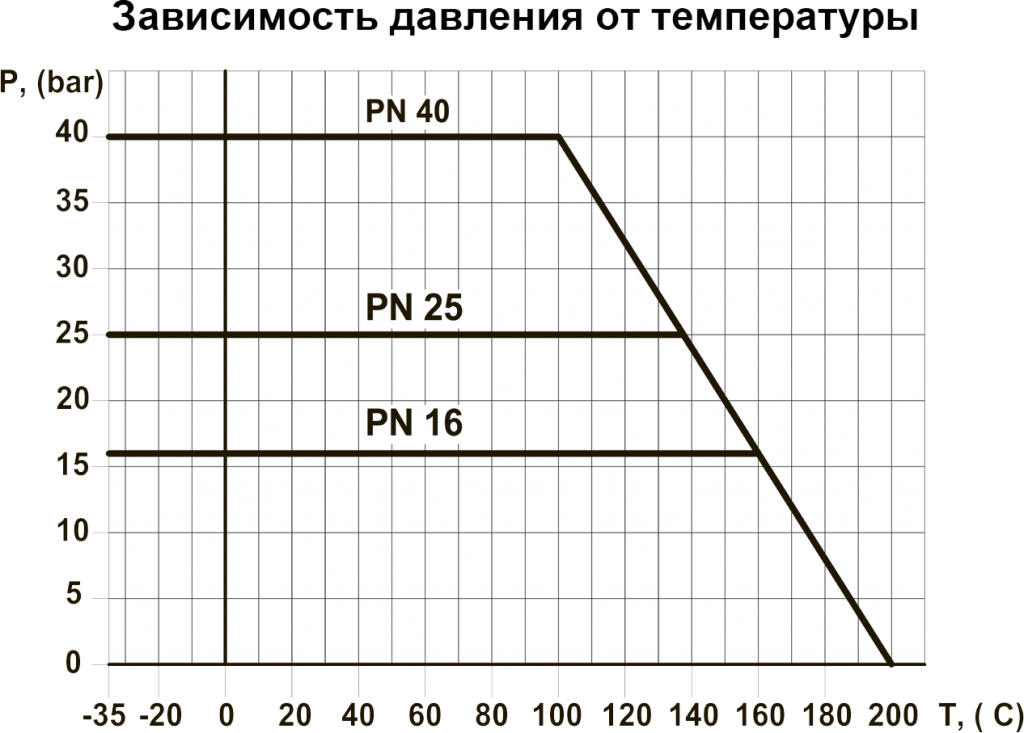
Использование графика давление-температура
Чтобы использовать график давления-температуры для определенного газа, либо известная температура, либо давление находятся на соответствующей оси, а альтернативное значение давления или температуры находится с помощью линии.
Пример
Для газа с приведенным ниже графиком давление-температура давление в точке 1 составляет 200 фунтов на квадратный фут, поэтому температура составляет 75°F; температура в точке 2 составляет 300 ° F, поэтому давление составляет 600 фунтов на квадратный фут. Линейная зависимость между давлением и температурой газа позволяет использовать график давления и температуры для оценки либо давления, либо температуры, если известен другой параметр.
Графики зависимости давления идеального газа от температуры показаны на рисунке. Выберите неверное утверждение
Вопрос
Обновлено:26/04/2023
A2Z-КИНЕТИЧЕСКАЯ ТЕОРИЯ ГАЗОВ И ТЕРМОДИНАМИКА-Уравнение идеального газа
20 видеоРЕКЛАМА
Текст Решение 9 0003
A
Плотность газа повышена на графике (i)
B
Плотность газа уменьшается на графике (ii)
C
Плотность газа постоянна на графике (iii)
D
Ничего из этого
Ответ
Правильный ответ C
Решение
ρ=PMRT
Плотность ρ остается постоянной, когда P/T или объем увеличиваются при постоянной температуре, поэтому объем уменьшается, поэтому плотность увеличивается .
На графиках (ii) и (iii) объем увеличивается, следовательно, плотность уменьшается. Обратите внимание, что объем был бы постоянным, если бы прямая линия на графике (iii) проходила через начало координат.
Ответить
Пошаговое решение, разработанное экспертами, чтобы помочь вам в решении вопросов и получении отличных оценок на экзаменах.
Ab Padhai каро бина объявления ке
Khareedo DN Pro и дехо сари видео бина киси объявление ки rukaavat ке!
Видео по теме
График зависимости давления от температуры идеального газа, как показано на рисунке. Соответствующий график зависимости плотности (rho) от объема (V) будет
11446313
График зависимости давления от температуры идеального газа показан на рисунке . Плотность газа в точке А равна Р0. Плотность в точке B будет равна
14155698
График зависимости давления от температуры идеального газа с равным количеством молей различных объемов построен так, как показано на рисунке.
Выберите правильные альтернативы.
17243245
График зависимости давления от плотности идеального газа показан на рисунке
17818002
График зависимости давления от температуры идеального газа показан на рисунке 2.39. Выберите неверное утверждение
254554671
График зависимости давления от температуры идеального газа показан на рисунке. Плотность газа в точке А равна ρ0. Плотность в точке B будет ____
606264315
График зависимости давления идеального газа от температуры показан на рисунке. Плотность газа в точке А равна rho_0. Плотность в B будет:
642778781
Графики зависимости давления идеального газа от температуры показаны на рисунке. Выберите неверное утверждение
643188829
График зависимости давления от температуры идеального газа при постоянном объеме V показан прямой линией A. Теперь масса газа удвоилась, а объем уменьшился вдвое, тогда соответствующий график зависимости давления от температуры будет показано линией
643188856
График зависимости давления идеального газа от плотности показан на рисунке
643188909
График зависимости давления идеального газа от температуры показан на рисунке.