Ответы | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука > Физика
| Похожие вопросы |
помогите решить с/р по физике:1.
Какую силу надо приложить к пробковому кубу с ребром 0,5 м,чтобы удержать его под водой? 2.Слиток золота и серебра…
Решено
На неподвижный бильярдный шар налетел…
железный кубик, лежащий на гладкой…
физика,помогите
лапласово давление
Пользуйтесь нашим приложением
| 45549. На горизонтальной плоскости лежат два бруска массами 1 кг и 4 кг, соединенные недеформированной пружиной. Какую наименьшую постоянную силу, направленную вдоль оси пружины, нужно приложить к первому бруску, чтобы сдвинулся и второй? Коэффициент трения брусков о плоскость 0,2. g = 10 м/с2. |
45550. На пружине жесткостью 100 Н/м к потолку подвешен груз. На груз начинает действовать постоянная сила 6 Н, направленная вертикально вниз. Найдите максимальное перемещение (в см) груза.
|
| 45551. Шары массами 1 кг и 2 кг движутся навстречу друг другу со скоростями 1 м/с и 2 м/с соответственно. Найдите, сколько теплоты выделится при неупругом ударе этих шаров. |
| 45552. Пуля массой 20 г, летящая со скоростью 100 м/с, застревает в деревянном шаре, летящем ей навстречу со скоростью 10 м/с. Считая, что масса шара гораздо больше массы пули, найдите количество теплоты, выделившееся при ударе. |
| 45553. |
45554. Диск массой 3 кг висит на упругом шнуре жесткостью 200 Н/м, прикрепленном к центру диска. Вдоль шнура с высоты 80 см на диск плашмя падает шайба (с отверстием в центре) массой 1 кг.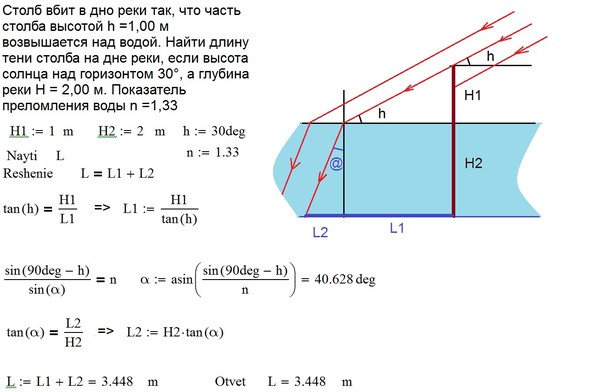 На какое расстояние (в см) опустится диск после падения шайбы ? Удар шайбы о диск абсолютно неупругий. g = 10 м/с2.
|
| 45555. В брусок массой 10 г, лежащий на гладком столе, попадает пуля массой 2 г, летящая со скоростью 60 м/с. На сколько миллиметров углубится пуля в брусок, если сила сопротивления движению пули в бруске равна 250 H? |
| 45556. На гладкой горизонтальной плоскости лежит доска длиной 1 м, на одном конце которой закреплен вертикальный упор. Какую минимальную скорость надо сообщить маленькому бруску, лежащему на другом конце доски, чтобы после абсолютно упругого удара об упор брусок вернулся назад и упал с доски? Масса доски в 8 раз больше, чем масса бруска, коэффициент трения между ними 0,2. g = 10 м/с2. |
| 45557. Из орудия массой 990 кг вылетает горизонтально снаряд массой 10 кг. Какая часть (в процентах) энергии, выделяющейся при взрыве пороховых газов, расходуется на откат орудия? |
45558. Человек массой 60 кг стоит на льду рядом с санями массой 40 кг. Человек толкает сани, сообщая им скорость 3 м/с, а сам откатывается в противоположную сторону. Какую работу совершает при этом человек?
|
| 45559. Движущийся снаряд разорвался на два осколка, угол между скоростями которых составил 60°. Один осколок имеет массу 20 кг и скорость 100 м/с, другой — массу 80 кг и скорость 25 м/с, Чему равна энергия (в кДж), выделенная при разрыве снаряда? |
| 45560. Две пружины, жесткости которых 5 Н/м и 20 Н/м, соединяют последовательно. Чему равна жесткость получившейся системы из двух пружин? |
| 45561. На парашютиста массой 80 кг в начале прыжка действует сила сопротивления воздуха, вертикальная составляющая которой 400 Н, а горизонтальная 300 Н. Найдите равнодействующую всех сил. g = 10 м/с2. |
45562. Между зданиями натянута проволока длиной 20 м, к середине которой прикреплен осветитель массой 20 кг. Каково натяжение проволоки, если она провисает на 50 см от того горизонтального уровня, на котором закреплены концы проволоки? g = 10 м/с2. Массу проволоки не учитывать.
|
| 45563. Тело массой 6 кг лежит на наклонной плоскости высотой 40 см и длиной основания 100 см. Какую минимальную горизонтальную силу надо приложить к телу, чтобы стащить его с наклонной плоскости, если коэффициент трения равен 0,5? g = 10 м/с2. |
| 45564. На наклонной плоскости высотой 3 м и длиной 9 м лежит тело массой 6 кг. Какую минимальную горизонтальную силу, направленную вдоль плоскости, надо приложить к телу, чтобы сдвинуть его с места? Коэффициент трения 0,5. g = 10 м/с2. |
| 45565. Два человека несут металлическую трубу, положив ее себе на плечи. Первый человек поддерживает трубу на расстоянии 1 м от ее конца, второй держит противоположный конец трубы. Во сколько раз нагрузка, приходящаяся на первого человека, больше, чем на второго, если длина трубы 2,5 м? |
45566. |
| 45567. К концам горизонтального стержня длиной 0,9 м и массой 2 кг подвешены два груза: слева — массой 1 кг, справа — массой 3 кг. На каком расстоянии (в см) от большей массы следует подпереть стержень, чтобы он оставался в равновесии? |
| 45568. Стержень массой 300 г согнули под прямым углом в точке, которая делит его в отношении 1:2, и подвесили на нити, привязанной к точке сгиба. Грузик какой массы (в г) надо прикрепить к концу короткой стороны угла, чтобы концы стержня находились на одном уровне? |
| 45569. Рабочий удерживает за один конец доску массой 16 кг так, что она опирается другим концом на землю и образует угол 60° с горизонтом. С какой силой удерживает рабочий доску, если эта сила перпендикулярна доске? g = 10 м/с2. |
45570. Лестница длиной 4 м приставлена к гладкой стене под углом 60° к горизонту. Коэффициент трения между лестницей и полом 0,25. На какое расстояние (в см) вдоль лестницы может подняться человек, прежде чем лестница начнет скользить? Массой лестницы пренебречь. |/ 3 = 1,7.
|
| 45571. Колесо радиусом 0,5 м и массой 10 кг стоит перед ступенькой высотой 0,1 м. Какую наименьшую горизонтальную силу надо приложить к оси колеса, чтобы поднять его на ступеньку? g = 10 м/с2. |
| 45572. Нижние концы лестницы-стремянки массой 10 кг соединены веревкой. Каждая сторона лестницы составляет с полам угол 45°. Считая пол абсолютно гладким, найдите натяжение веревки. g = 10 м/с2. |
| 45573. В кузове грузовика стоит цилиндр, радиус основания которого 10 см, а высота 50 см. С каким максимальным ускорением может тормозить грузовик, чтобы цилиндр не опрокинулся? g = 10 м/с2. |
45574. Два одинаковых шара радиусом 10 см и массой 600 г каждый положили в вертикальный открытый с обеих сторон тонкостенный цилиндр радиусом 15 см, стоящий на горизонтальной плоскости. Пренебрегая трением, найдите, при какой минимальной массе (в г) цилиндра шары его не опрокидывают.
|
| 45575. Два шара радиусами 1 см и 6 см соединены однородным стержнем длиной 10 см. Масса первого шара 60 г, масса второго — 72 г, масса стержня 12 г. Найдите расстояние (в см) от центра тяжести системы до центра меньшего шара. |
| 45576. Однородная тонкая пластина имеет форму треугольника со сторонами 13 см, 14 см и 15 см. На каком расстоянии (в см) от второй стороны находится центр тяжести пластины? |
| 45577. В вершинах треугольника ABC находятся, соответственно, массы 4, 6 и 10 г. Стороны треугольника равны: АВ = 50см, ВС = 40 см и СА = 30 см. На каком расстоянии (в см) от стороны ВС находится центр тяжести системы? |
45578. Две стороны проволочной рамки, имеющей форму равностороннего треугольника со стороной 1 м, сделаны из алюминиевой проволоки, а третья — из медной такого же диаметра. На каком расстоянии (в см) от середины медной проволоки находится центр тяжести системы? Плотность меди в 3 раза больше плотности алюминия. |/ 3 = 1,7.
|
| 45579. В однородном диске радиусом R вырезано круглое отверстие радиусом R/3. Центр выреза находится на расстоянии 24 см от центра диска. На каком расстоянии (в см) от центра диска находится центр масс этого тела? |
| 45580. Отверстие в дне нефтяного бака заделано цилиндрической пробкой. Чтобы выдавить пробку наружу, надо приложить к ней силу 16 H. До какой предельной высоты можно наливать в этот бак нефть, если площадь пробки 10 см2? Плотность нефти 800 кг/м3. g = 10 м/с2. |
45581. В полый куб налита доверху жидкость. Во сколько раз сила давления воды на дно больше силы давления на боковую стенку? Атмосферное давление не учитывать.
|
| 45582. Цистерна имеет форму лежащего на боку цилиндра диаметром 1 м. Через отверстие в верхней части цистерну доверху заполнили водой. С какой силой действует вода на вертикальную стенку цистерны? п = 3,14. g = 10 м/с2. |
| 45583. Вертикальная труба с поршнем, плотно прилегающим к ее внутренним стенкам, опущена нижним концом в воду. Вначале поршень находился в самом нижнем положении, на уровне воды, а затем его медленно поднимают на высоту 20 м. Пренебрегая трением, найдите совершенную при этом работу (в кДж). Площадь поршня 100 см2. Атмосферное давление 100 кПа. g = 10 м/с2. |
| 45584. В сосуд с водой вставлена трубка сечением 2 см2. В трубку налили масло массой 72 г. Плотность масла 900 кг/м3. Найдите разность (в см) между верхними уровнями масла и воды. |
45585. В сообщающиеся сосуды с ртутью долили: в один сосуд столб масла высотой 30 см, в другой сосуд столб воды высотой 20,2 см. Определите разность уровней (в мм) ртути в сосудах. Плотность ртути 13600 кг/м3, масла 900 кг/м3.
|
| 45586. В сообщающихся сосудах находится ртуть. Площадь сечения одного сосуда в 2 раза больше, чем другого. В узкий сосуд наливают столб воды высотой 1,02 м. На сколько миллиметров поднимется ртуть в широком сосуде? Плотность ртути 13600 кг/м3. |
| 45587. Вес тела в воде в 2 раза меньше, чем в воздухе. Какова плотность вещества тела? Ответ дайте в г/см3. |
| 45588. Решите задачу Архимеда — найдите массу золота (в г) в короне, изготовленной из сплава золота с серебром. Вес короны в воздухе 25,4 Н, в воде — 23,4 H. Плотность золота 19,3 г/см3, серебра — 10,5 г/см3. g = 10 м/с2. |
| 45589. Стеклянный шарик объемом 1 см2 равномерно падает в воде. При перемещении шарика на 10 м выделяется 0,17 Дж тепла. Найдите плотность стекла. g = 10 м/с2. |
45590. Один конец нити закреплен на дне, а второй прикреплен к пробковому поплавку. При этом 75% всего объема поплавка погружено в воду. Определите силу натяжения нити, если масса поплавка равна 2 кг. Плотность пробки 300 кг/м3. g = 10 м/с2.
|
| 45591. Тонкая однородная палочка шарнирно укреплена за верхний конец. Нижняя часть палочки погружена в воду, причем равновесие наступает тогда, когда палочка расположена наклонно к поверхности воды и в воде находится половина палочки. Какова плотность материала, из которого сделана палочка? |
| 45592. Льдина площадью 1 м2 и толщиной 0,4 м плавает в воде. Какую минимальную работу надо совершить, чтобы полностью погрузить льдину в воду? Плотность льда 900 кг/м3. g = 10 м/с2. |
| 45593. В цилиндрический сосуд с площадью дна 100 см2 налита вода. На какую величину изменится давление на дно сосуда, если на поверхности воды будет плавать кусок льда массой 300 г? g = 10 м/с2.
|
| 45594. Полый шар плавает в жидкости, наполовину погрузившись в нее. Какую долю объема шара (в процентах) составляет его внутренняя полость? Плотность жидкости в 2 раза меньше плотности вещества шара. |
| 45595. Тело плавает на границе двух жидкостей. Плотность тяжелой жидкости в 2,5 раза больше плотности тела, а плотность легкой — в 2 раза меньше плотности тела. Какая часть объема тела (в процентах) погружена в тяжелую жидкость? |
| 45596. Открытый сосуд с жидкостью находится в лифте, который опускается с ускорением 2 м/с2. На сколько процентов давление в некоторой точке жидкости меньше, чем давление в этой же точке в покоящемся сосуде? Атмосферное давление не учитывать. g = 10 м/с2. |
| 45597. Цистерну в форме куба со стороной 2 м, стоящую на платформе заполнили водой почти доверху и закрыли. Платформа стала разгоняться с горизонтальным ускорением 2 м/с2. Найдите силу давления (в кН) воды на заднюю стенку цистерны. Атмосферное давление не учитывать. g = 10 м/с2.
|
| 45598. Открытую цистерну в формe куба со стороной 2 м, стоящую на платформе, заполнили жидкостью наполовину. Платформа стала разгоняться с ускорением 2 м/с2. Насколько поднялся уровень (в см) жидкости у задней стенки платформы к тому моменту, когда жидкость и платформа стали двигаться как единое целое? g = 10 м/с2. |
| 45599. Тело плотностью 500 кг/м3 плавает на поверхности воды в сосуде, который поднимается вертикально вверх с ускорением g/2. Какая часть объема тела (в процентах) погружена в воду? |
| 45600. К потолку цистерны, целиком заполненной водой, которая движется с горизонтальным ускорением 2,25 м/с2, подвешен на нити шар массой 5 кг. Найдите натяжение нити после того, как она займет устойчивое наклонное положение. Плотность материала шара 5000 кг/м3. g = 10 м/с2. |
| 45601. После того, как в комнате включили электрокамин, температура воздуха повысилась от 18°С до 27°С при неизменном давлении. На сколько процентов уменьшилось число молекул воздуха в комнате?
|
| 45602. Какова полная кинетическая энергия (в кДж) поступательного движения молекул газа, находящихся в баллоне емкостью 5 л при давлении 800 кПа? |
| 45603. Средняя квадратичная скорость молекул газа равна 1000 м/с. Чему будет равна средняя квадратичная скорость после увеличения давления и объема газа в 1,2 раза? |
| 45604. Какова была начальная температура (в Кельвинах) воздуха, если при нагревании его на 3 К объем увеличился на 1 % от первоначального? Процесс изобарный. |
| 45605. Газ находится в вертикальном цилиндре под поршнем массой 5 кг. Какой массы груз надо положить на поршень, чтобы он остался в прежнем положении, когда абсолютная температура газа будет увеличена вдвое? Атмосферное давление 100 кПа, площадь поршня 0,001 м2. 5 Па. После трех ходов поршня откачивающего насоса давление воздуха упало до 800 Па. Определите, во сколько раз объем цилиндра насоса больше объема сосуда. Температура постоянна.
|
| 45609. Воздух находится в вертикальном цилиндре под поршнем массой 20,2 кг и сечением 20 см2. После того, как цилиндр стали перемещать вертикально вверх с ускорением 5 м/с2, высота столба воздуха в цилиндре уменьшилась на 20%. Считая температуру постоянной, найдите атмосферное давление (в кПа). g = 10 м/с2. |
| 45610. В трубке, закрытой с одного конца, столбик воздуха заперт столбиком ртути длиной 19 см. Если трубку повернуть открытым концом вниз, длина столбика воздуха будет 10 см, а если открытым концом вверх, то 6 см. Найдите атмосферное давление (в мм рт. ст.). |
| 45611. В длинной горизонтальной трубке, открытой с одного конца, столбик воздуха длиной 16 см заперт столбиком ртути длиной 20 см. Трубку приводят во вращение вокруг вертикальной оси, проходящей через ее закрытый конец. При какой угловой скорости столбик ртути сместится на 4 см? Атмосферное давление 750 мм рт.ст. g = 10 м/с2.
|
| 45612. Газ, занимающий при температуре 127°С и давлении 200 кПа объем 3 л, изотермически сжимают, затем изобарно охлаждают до температуры -73°С, после чего изотермически изменяют объем до 1 л. Найдите конечное давление (в кПа) газа. |
| 45613. Теплоизолирующий поршень делит горизонтальный сосуд на две равные части, содержащие газ при температуре 7°С. Длина каждой части 30 см. Когда одну часть сосуда нагрели, поршень сместился на 2 см. На сколько градусов нагрели газ? Температура газа в другой части сосуда не изменилась. |
| 45614. Баллон емкостью 40 л содержит сжатый воздух под давлением 18 МПа при 27°С. Какой объем (в л) воды можно вытеснить из цистерны подводной лодки воздухом этого баллона, если лодка находится на глубине 20 м, где температура 7°С? Атмосферное давление 0,1 МПа, g = 10 м/с2.
|
| 45615. Какую массу (в г) водорода содержал баллон, если он взорвался при температуре 1172 К и был рассчитан на хранение азота массой 7 кг при температуре 293 К при десятикратном запасе прочности? Молярная масса водорода 2 кг/кмоль, азота — 28 кг/кмоль. |
| 45616. По газопроводу течет углекислый газ при давлении 0,83 МПа и температуре 27°С. Какова скорость течения газа в трубе, если за 2,5 мин через поперечное сечение трубы площадью 5 см2 протекает 2,2 кг газа? Молярная масса углекислого газа 44 кг/кмоль, универсальная газовая постоянная 8300 Дж/(кмоль*К). |
| 45617. Баллон содержит газ при 27°С и давлении 200 кПа. Каково будет давление (в кПа), если из баллона выпустить 80% газа и охладить его до 12° C? |
| 45618. Два одинаковых сосуда соединены трубкой, объемом которой можно пренебречь. Система наполнена газом и находится при температуре 300 К. Когда один из сосудов был нагрет, а другой оставлен при прежней температуре, давление в системе увеличилось в 1,5 раза. На сколько градусов был нагрет один из сосудов?
|
| 45619. При повышении температуры азота, заключенного в закрытый сосуд, от 7°С до 1407°С третья часть молекул азота распалась на атомы. Во сколько раз при этом возросло давление газа? |
| 45620. При работе электромотора мощностью 400 Вт он нагревается на 10 К за 50 с непрерывной работы. Чему равен КПД (в процентах) мотора? Теплоемкость мотора 500 Дж/К. |
| 45621. Генератор излучает импульсы сверхвысокой частоты с энергией в каждом импульсе 6 Дж. Частота повторения импульсов 700 Гц. КПД генератора 60%. Сколько литров воды в час надо пропускать через охлаждающую систему генератора, чтобы вода нагрелась не выше, чем на 10 К? Удельная теплоемкость воды 4200 Дж/(кг*К). |
| 45622. Для нагревания некоторой массы воды от 0°С до 100°С требуется 8400 Дж теплоты. Сколько еще потребуется теплоты (в кДж), чтобы полностью испарить эту воду? Удельная теплоемкость воды 4200 Дж/(кг*К), удельная теплота парообразования воды 2300 кДж/кг. 5 Дж/кг. Ответ дать в минутах.
|
| 45624. Вычислите КПД (в процентах) газовой горелки, если в ней используется газ с теплотой сгорания 36 МДж/м3, а на нагревание чайника с 3 л воды от 10°С до кипения было израсходовано 60 л газа. Теплоемкость чайника 600 Дж/К. Удельная теплоемкость воды 4200 Дж/(кг*К). |
| 45625. Чему равна высота водопада, если температура воды у его основания на 0,05°С больше, чем у вершины? Считать, что вся механическая энергия идет на нагревание воды. Удельная теплоемкость воды 4200 Дж/(кг*К), g = 10 м/с2. |
| 45626. На какую высоту можно было бы поднять груз массой 100 кг, если бы удалось полностью превратить в работу энергию, выделяющуюся при охлаждении стакана воды от 100°С до 20°С? Масса воды в стакане 250 г, удельная теплоемкость воды 4200 Дж/(кг*К), теплоемкость стакана не учитывать, g = 10 м/с2. |
| 45627. Тело соскальзывает с наклонной плоскости длиной 260 м и углом наклона 60°. Коэффициент трения о плоскость 0,2. Определите, на сколько градусов повысится температура тела, если на его нагревание идет 50% выделившегося тепла. Удельная теплоемкость материала, из которого сделано тело, равна 130 Дж/(кг*К), g = 10 м/с2.
|
| 45628. Два одинаковых шарика, сделанных из вещества с удельной теплоемкостью 450 Дж/(кг*К), движутся навстречу друг другу со скоростями 40 м/с и 20 м/с. Определите, на сколько градусов они нагреются в результате неупругого столкновения. |
| 45629. С какой высоты (в км) должен падать оловянный шарик, чтобы при ударе о поверхность он полностью расплавился? Считать, что 50% энергии шарика идет на его нагревание и плавление. Начальная температура шарика 32°С. Температура плавления олова 232°С, его удельная теплоемкость 200 Дж/(кг*К), удельная теплота плавления 58 кДж/кг. g = 9,8 м/с2. |
| 45630. Для приготовления ванны емкостью 200 л смешали холодную воду при 10°С с горячей при 60°С Сколько литров холодной воды нужно взять, чтобы в ванне установилась температура 40°С? |
| 45631. 6 Дж/кг.
|
| 45634. Ванну емкостью 85 л необходимо заполнить водой, имеющей температуру 30°С, используя воду при 80°С и лед при температуре -20°С. Определите массу льда, который следует положить в ванну. Удельная теплота плавления льда 336 кДж/кг, удельная теплоемкость льда 2100 Дж/(кг*К), удельная теплоемкость воды 4200 Дж/(кг*К). |
| 45635. В сосуде имеется некоторое количество воды и такое же количество льда в состоянии теплового равновесия. Через сосуд пропускают водяной пар при температуре 100°С. Найдите установившуюся температуру воды в сосуде, если масса пропущенного пара равна первоначальной массе воды. Удельная теплоемкость воды 4200 Дж/(кг*К), удельная теплота парообразования воды 2,3 МДж/кг, удельная теплота плавления льда 330 кДж/кг. |
| 45636. В цилиндре с площадью основания 100 см2 находится газ при температуре 300 К. На высоте 30 см от основания цилиндра расположен поршень массой 60 кг. Какую работу совершит газ при расширении, если его температуру медленно повысить на 50°С? Атмосферное давление 100 кПa, g = 10 м/с2.
|
| 45637. Один моль газа изохорно охладили так, что его давление уменьшилось в 5 раз, а затем изобарно нагрели до начальной температуры 400 К. Какую работу совершил газ? Универсальная газовая постоянная 8300 Дж/(кмоль*К). |
| 45638. Идеальный газ в количестве 4 моль расширяют так, что его давление изменяется прямо пропорционально объему. Чему равна работа газа при увеличении его температуры на 10 К? Универсальная газовая постоянная 8300 Дж/(кмоль*К). |
| 45639. В изотермическом процессе газ совершил работу 1000 Дж. На сколько увеличится внутренняя энергия этого газа, если ему сообщить количество теплоты, вдвое большее, чем в первом процессе, а процесс проводить изохорно? |
| 45640. Для нагревания некоторого количества идеального газа с молярной массой 28 кг/кмоль на 14 К при постоянном давлении потребовалось 29 Дж теплоты. Чтобы затем охладить этот же газ до исходной температуры при постоянном объеме, у него надо отнять 20,7 Дж теплоты. Найдите массу (в г) газа. Универсальная газовая постоянная 8300 Дж/(кмоль*К).
|
| 45641. Некоторое количество идеального одноатомного газа при изобарном нагревании получает 10 Дж теплоты. Какую работу совершит этот газ при адиабатическом охлаждении до первоначальной температуры? |
| 45642. Идеальный одноатомный газ в количестве 1 моль нагрели сначала изохорно, а затем изобарно. В результате как давление, так и объем газа увеличились в два раза. Какое количество теплоты получил газ в этих двух процессах, если его начальная температура была 100 К? Универсальная газовая постоянная 8300 Дж/(кмоль*К). |
| 45643. Два теплоизолированных сосуда одинакового объема соединены тонкой трубкой с краном. В одном сосуде находится гелий при температуре 200 К, а в другом — гелий при температуре 400 К и при давлении в 3 раза большем, чем в первом сосуде. Какой станет температура газа после открывания крана и установления теплового равновесия?
|
| 45644. В вертикальном теплоизолированном цилиндре под поршнем находится некоторое количество гелия при температуре 240 К. На поршне лежит груз массой, равной половине массы поршня. Груз мгновенно убирают и дожидаются прихода системы к равновесию. Чему станет равна температура (в Кельвинах) газа? Над поршнем газа нет. |
| 45645. Рабочее тело идеальной тепловой машины, работающей по циклу Карно, получает от нагревателя с температурой 273°С количество теплоты 80 кДж. Роль холодильника играет окружающий воздух, температура которого 0°С. На какую максимальную высоту эта машина может поднять груз массой 400 кг? g = 10 м/с2. |
| 45646. Два моля газа изобарно нагревают от 400 К до 800 К, затем изохорно охлаждают до 500 К. Далее газ охлаждают изобарно так, что его объем уменьшается до первоначального. Наконец, газ изохорно нагревают до 400 К. 5 Дж/кг.
|
OpenStax College Physics Solution, глава 14, задача 74 (задачи и упражнения)
Chapter 14 question:
1PE2PE3PE4PE5PE6PE7PE8PE9PE10PE11PE12PE13PE14PE15PE16PE17PE18PE19PE20PE21PE22PE23PE24PE25PE26PE27PE28PE29PE30PE31PE32PE33PE34PE35PE36PE37PE38PE39PE40PE41PE42PE43PE44PE45PE46PE47PE48PE49PE50PE51PE52PE53PE54PE55PE56PE57PE58PE59PE60PE61PE62PE63PE64PE65PE66PE67PE68PE69PE70PE71PE72PE73PE74PE75PE76PE77PE78PE79{-4}$
Видеорешение
Зарегистрируйтесь, чтобы просмотреть видеорешение!
Начать бесплатную неделю
Trustpilot
Рейтинг
ПлохоНе так уж плохоСреднеХорошоОчень хорошо
1 голос с рейтингом 5
Скриншоты калькулятора
Стенограмма видео
Это ответы по физике в колледже с Шоном Дычко. Некоторое количество воды падает с высоты 55,0 метров над Ниагарским водопадом, а удельная теплоемкость воды составляет 4186 Дж на килограмм на градус Цельсия. Теперь, когда вода достигает дна водопада, кинетическая энергия, которую она приобрела, знаете ли, из-за потери потенциальной гравитационной энергии, затем превратится в тепло, и поэтому это тепло будет равно, знаете ли, кинетической энергии. это теряется в первую очередь, но кинетическая энергия, которая у него была в первую очередь, связана с потенциальной энергией, которая была у него на вершине водопада. Таким образом, количество теплоты, полученное водой, равно 9.0043 mgh , потерянная потенциальная энергия. Это тепло также будет массой воды, умноженной на ее удельную теплоемкость, умноженную на изменение температуры, поэтому мы можем приравнять эти два числа и сказать, что mcΔT равно mgh , а затем разделить обе части на mc , тогда мы можем найти изменение температуры равно gh , деленное на c . Итак, 9,80 ньютона на килограмм умножить на 55,0 метра, деленное на удельную теплоемкость воды — 4186, и это 0,129 градуса Цельсия. Часть (б) спрашивает нас, какая часть воды должна испариться, чтобы компенсировать это повышение температуры. .. другими словами, чтобы поддерживать постоянную температуру? Итак, сколько воды нужно испарить, чтобы поглотить всю энергию, которую она перевела из потенциальной энергии в тепло? Хорошо! Итак, мы скажем, что масса испарения, умноженная на скрытую теплоту испарения при 37,0 градусах, потому что это цифра, которую мы привели в учебнике, которая лучше, чем скрытая теплота парообразования при 100,0 градусах, все это равно потенциальной энергии. Так это м всего здесь, общая масса, умноженная на г умноженная на начальную высоту. Итак, мы разделим обе части на общую массу, а также разделим обе части на скрытую теплоту парообразования, и мы получим, что доля массы, которая должна испариться, равна gh , деленная на скрытую теплоту парообразования. Таким образом, 9,80 умножить на 55,0 разделить на 2430 умножить на 10 до 3, и мы получим 2,22 умножить на 10 до минус 4 — это доля, которая должна испариться, чтобы поддерживать постоянную температуру.
Solutions for problems in chapter 14
1PE2PE3PE4PE5PE6PE7PE8PE9PE10PE11PE12PE13PE14PE15PE16PE17PE18PE19PE20PE21PE22PE23PE24PE25PE26PE27PE28PE29PE30PE31PE32PE33PE34PE35PE36PE37PE38PE39PE40PE41PE42PE43PE44PE45PE46PE47PE48PE49PE50PE51PE52PE53PE54PE55PE56PE57PE58PE59PE60PE61PE62PE63PE64PE65PE66PE67PE68PE69PE70PE71PE72PE73PE74PE75PE76PE77PE78PE79PE
Накачать хранилище | Подсчитайте
Если мы примем солнечную и ветровую энергию в качестве основных компонентов нашей энергетической инфраструктуры, поскольку мы отлучены от ископаемого топлива, нам придется серьезно решать проблему хранения энергии. Предыдущий пост продемонстрировал, что у нас, вероятно, недостаточно материалов в мире, чтобы просто создавать гигантские свинцово-кислотные (или никелевые, или литиевые) батареи для выполнения этой работы. В комментариях часто указывалось на гидроаккумулирование как на гораздо более разумный ответ. Действительно, в настоящее время насосное хранилище является доминирующим — и почти единственным — решением для хранения данных в сетевом масштабе. Здесь мы взглянем на насосную гидроэнергетику и оценим, что она может сделать для нас.
Основы гравитационного хранения
Когда вы поднимаете объект, вы должны приложить силу для противодействия гравитации (вес объекта) и применить эту силу на высоте , на которую вы поднимаете объект. Вес объекта — и, следовательно, сила, приложенная для его подъема, — это его масса, умноженная на ускорение свободного падения (применение ньютоновского уравнения F = мА ; в этом случае мг , где г — это гравитационное ускорение, или около 10 м/с²). Работа определяется как сила, умноженная на расстояние, поэтому подъем объекта массой м высота h приводит к затратам энергии (работы) в размере мгч . Это называется гравитационной потенциальной энергией .
Это называется потенциальной энергией, потому что можно положить вложенную энергию на полку — фактически буквально — чтобы получить к ней доступ позже. Упавший кирпич, которому ранее была передана гравитационная потенциальная энергия, может выполнять полезную работу, например, забивать гвоздь в кусок дерева (огромная сила, умноженная на малое расстояние = та же самая работа). Сохраненная энергия не ухудшается со временем ни на йоту: в этом смысле она представляет собой идеальное долговременное хранилище.
Идея насосного гидроаккумулирования заключается в том, что мы можем закачивать массу воды в резервуар (на шельф), а затем извлекать эту энергию по желанию, исключая потери на испарение. Насосы и турбины (на самом деле часто реализованные как одна и та же физическая единица) могут быть примерно на 90% эффективнее, поэтому хранение в оба конца обходится весьма скромно.
Концепция гидроаккумулятора Раккун-Маунтин.
Основная проблема с гравитационным накопителем заключается в том, что он невероятно слаб по сравнению с химическими методами, технологиями сжатого воздуха или маховиками (см. пост о вариантах домашнего хранения энергии). Например, чтобы получить количество энергии, хранящейся в одной батарейке АА, нам пришлось бы поднять 100 кг (220 фунтов) на 10 м (33 фута), чтобы соответствовать этому значению. Чтобы соответствовать энергии, содержащейся в галлоне бензина, нам пришлось бы поднять 13 тонн воды (3500 галлонов) на высоту в один километр (3280 футов). Ясно, что плотность энергии гравитационного накопителя находится в крайне невыгодном положении.
Недостаток плотности энергии мы компенсируем объемом. Озера воды за плотинами, например, представляют собой значительное хранилище.
Сила потока
Когда вода выходит из нижней части плотины, она переносит энергию, как если бы она была «отложена» на поверхность озера за плотиной. Откуда вода на дне «знает», насколько высока поверхность озера? Давление, пропорциональное весу воды над головой. Итак, давайте возьмем кубический метр воды массой 1000 кг и направим его через турбину. мгч энергии в кубе воды для плотины высотой 100 м составляет (1000 кг)(10 м/с²)(100 м) = 10 6 Дж, или один мегаджоуль.
Если через эту плотину высотой 100 м протекает только один кубический метр в секунду, она будет производить 1 МДж/сек, или 1 МВт. Я игнорирую примерно 90% КПД гидроэлектрических турбин, чтобы цифры были аккуратными и приблизительными. Как правило, скорость потока измеряется в диапазоне 1000 м³/с, так что наша 100-метровая плотина будет производить 1 ГВт в этом масштабе.
Таким образом, рецепт для понимания гидроэлектростанции прост: умножьте высоту воды за плотиной (в метрах) на скорость потока в десять тысяч раз в кубических метрах в секунду, чтобы получить мощность в ваттах.
Нам нужно
Как Много памяти? Энергетическая диета в США составляет около 3×10 12 Вт или 3 ТВт. Две трети этого объема питают тепловые двигатели (электростанции, автомобили и т. д.) со средней эффективностью 30 %, выполняя в придачу 0,6 ТВт полезной работы. Другой 1 ТВт – это прямое тепло (большая его часть приходится на промышленное технологическое тепло) и электроэнергия от ядерных и гидроисточников. Если представить, что мы заменим наши тепловые двигатели прямой электроэнергией и электрифицированным транспортом, нам потребуется около 2 ТВт общей мощности с учетом некоторой неэффективности. Если вас устраивает половина этого значения, прекрасно — два фактора качественно не изменят гигантский масштаб проблемы.
Следующий вопрос: как долго нам понадобится наше хранилище? В посте о батарее национального размера я утверждал, что нам нужно 7 дней хранения, чтобы она была невидима для конечного пользователя. То есть, если американцы настаивают на том, чтобы не менять ни одной из своих привычек и иметь ноль перебоев в хранении в течение десяти лет (читайте о полном отключении Сан-Диего во время недавнего отключения электроэнергии в округе), то 7 дней — это вероятно, не далеко от отметки. Я получил критику за этот выбор, но я использую его снова здесь, потому что А) это не так уж и неразумно, Б) это позволяет провести параллельное сравнение с расчетом национальной батареи, и В) вы увидите, что это не делает или разбить корпус: даже один день хранения — это сверхсложно. Разделите все мои числа на 7, если вы хотите, чтобы я использовал, например, один день хранения.
Обратите внимание, что 7 дней хранения буквально не означают, что мы готовы провести 7 дней без использования возобновляемой инфраструктуры. Работа на уровне 30% от суммы безубыточности в течение 10 дней также оставляет систему с 7-дневным дефицитом энергии, например. Это обстоятельство нетрудно представить: пасмурная зимняя неделя над юго-западом, а скорость ветра над страной в два раза меньше среднего значения (т. е. в восемь раз меньше силы) за тот же период.
Таким образом, 2 ТВт на 7 дней означают 336 миллиардов кВт⋅ч емкости хранения.
Гидронасосная установка First Blush
Какой объем хранилища потребовался бы, если бы мы реализовали схему гидронасосной гидроэнергетики? Одним из непосредственных ориентиров масштаба является то, что у нас есть 78 ГВт установленной гидроэлектроэнергии в США, что составляет 4% от целевого спроса в 2 ТВт. Наша традиционная гидроэнергетика не может быть увеличена даже в два раза, поскольку основные речные участки уже вырваны.
А как насчет возможных насосных гидроустановок: не на текущих реках, а в горах, где мы могли бы отгородить высокую долину и наполнить ее водой?
Я говорю горы, потому что нам нужна значительная разница высот для гидроаккумулятора, чтобы иметь смысл. Мы не увидим гидроаккумуляторы на равнинах. Расстояние по горизонтали тоже нужно минимизировать, поэтому нужен резкий рельеф — то есть горы.
В первом приближении горы можно представить себе глыбами. У них заостренные вершины, которые смотрят вверх. Они явно не очень похожи на чаши. Перевернутые миски, может быть. Однако они часто образуют ложбины («вопли» в некоторых частях), окруженные рукавами / гребнями горы. Загородив вход в лощину, мы можем заполнить эту бесполезную пустоту водой. Пищу и сурка можно просто научиться плавать! Нам также нужен еще один водоем такого же объема внизу, чтобы собирать воду в цикле хранения.
Не могу сказать, что изучал топографию наших земель, чтобы увидеть, сколько мест поддается этим грандиозным инженерным чудесам. Я могу не обращать внимания на широко распространенное существование естественных чаш, расположенных на краях скал. Как бы то ни было, 22 ГВт гидроаккумулирующих мощностей, которые мы с по , в настоящее время, по-видимому, выбрали в первую очередь. Вместо того, чтобы возиться с топографическими картами, я использую простую «полую» модель, основанную на моем пребывании в горах и рассматривании карт рельефа.
В любом случае, давайте не будем позволять этим деталям мешать нам заниматься математикой! Допустим, наша средняя предполагаемая впадина допускает стену высотой 500 м (1650 футов) на одном конце и еще одну стену высотой в несколько сотен метров ниже для нижнего резервуара (впадина здесь шире — может быть, к настоящему времени даже долина — так что тот же объем вмещается за счет меньшей глубины и большей площади).
Простая модель для заполнения дупла водой на высоту, выс.
Моя модель дупла будет иметь V-образный профиль, боковые стороны которого будут иметь уклон 20 %, а полое дно будет подниматься вверх с 10 % уклоном. Таким образом, стена плотины высотой 500 м имеет 5 км в поперечнике вверху, а озеро простирается на 5 км назад треугольником. Эта геометрия создает резервуар объемом 2 кубических километра. Учитывая сужающуюся форму, накопленная гравитационная потенциальная энергия составляет 2 миллиарда кВтч. Нам просто нужно построить 170 таких штук. Не говоря уже о том, что мы никогда не строили стены таких размеров. Или тот факт, что крупнейшая на сегодняшний день гидроаккумулирующая станция хранит 0,034 млрд кВтч — в 60 раз меньше мощности.
Но давайте продолжим игру: если мы действительно требуем 2 ТВт мощности примерно от 170 гидроэлектростанций, мы говорим о 12 ГВт производственной мощности каждой. Это значительно больше, чем у крупнейшей гидроэлектростанции в США (Гранд-Кули, 6,8 ГВт). Times 170.
Возможно, я был слишком амбициозен, начав с высоты плотины 500 м. Большее количество меньших водохранилищ позволило бы создать более разумные электростанции и, возможно, избежать превращения семи чудес света в 177 чудес света (с большим количеством избыточности).
Энергия, хранящаяся в отгороженной стеной пустоте, масштабируется, как высота резервуара, в четвертой степени ! Так что, если мы спустимся на высоту 250 м (что для меня все еще впечатляет, поскольку выше плотины Гувера), нам потребуется в 16 раз больше установок (более 2500), каждая мощностью 600 МВт. Для масштаба в настоящее время у нас есть 24 гидроэлектростанции в США мощностью более 600 МВт.
Плотина Гувера: высота 221 м; мощность 2,0 ГВт; 2,5 миллиона кубометров бетона.
Я думаю, на этом этапе вы можете понять, почему споры о необходимости 1 TW против 2 TW или о необходимости 2 дней хранения вместо 7 дней не помогут решить тупик сложной проблемы. Даже выполнение хотя бы 1% изложенных мной требований было бы супер-впечатлением.
Весь этот бетон!
Для этих стен плотины потребуется много бетона. Обзор конструкции плотины показывает, что толщина основания составляет примерно 65–90% высоты плотины. Выбирая 75% и сужаясь к выступу, наша предыдущая геометрия требует объема бетона на 25% больше, чем ч ³, где ч — высота плотины. Для нашего 250-метрового комплекса плотин нам нужно 19 миллионов кубометров бетона на каждую. Каждая плотина содержит столько же бетона, сколько существует в плотинах Трех ущелий и Гранд-Кули вместе взятых! А это « Маленькая » версия нашей плотины. А нам нужно более 2500 из них. Я просто говорю.
При стоимости энергии 2,5 ГДж на тонну бетона и плотности 2,4 тонны на кубический метр нам в конечном итоге потребуется 32 миллиарда кВтч энергии на плотину, а всего 90 трлн кВтч. Это более чем в 250 раз превышает количество энергии, поглощаемой плотинами, и представляет собой три года из общих энергетических аппетитов США сегодня.
Обратите внимание, что я полностью игнорирую требования к нижнему резервуару.
Просторная комната для катания на водных лыжах
Теперь мне очень хочется понять, как это выглядит относительно нашего ландшафта. Какую площадь займут все эти озера?
В модели высоты плотины 500 м площадь верхнего водохранилища составляет 12,5 квадратных километров. Раз 170 водохранилищ это 2125 квадратных километров. В модели 250 м у нас есть 3 квадратных километра на водохранилище, или 8500 км² для всего набора. Таким образом, общая необходимая площадь пропорциональна обратному квадрату характерной высоты плотины.
Нам также нужно добавить площадь для нижнего резервуара. Так как рельеф ниже, вероятно, менее наклонен, давайте предположим, что площадь поверхности нижнего водохранилища в два раза больше площади верхнего водохранилища, поэтому теперь у нас есть около 25 000 км² площади нового озера (оба водохранилища не заполнены одновременно, но эта земля негде строить торговый центр).
Получаем площадь, эквивалентную 160 км по стороне. Это такая же площадь, как озеро Эри (и больше его объема). Добавьте на карту еще одно место, равное Великому озеру. Не тривиальное дело. Я еще не спросил, где мы берем воду для этого предприятия. Хорошо, что нехватка воды не беспокоит эту планету.
Стоит также сравнить с площадью фотоэлектрической системы, обеспечивающей 2 ТВт средней мощности. Для такой производительности потребуется 10 ТВт установленной мощности (с учетом дня и ночи, угла наклона солнца, погоды). При КПД 15% и пиковой солнечной энергии 1 кВт/м² нам потребуется около 65 000 квадратных километров панелей — примерно сопоставимые масштабы. Имейте в виду, что акватория основана на более чем 2500 гигантских 250-метровых плотинах, каждая из которых выше плотины Гувера и содержит в 8 раз больше бетона. Для небольших, более реалистичных проектов площадь воды может легко превышать площадь солнечной панели. Преобразование земли в гидроаккумулирование несет далеко большее воздействие на окружающую среду, чем преобразование в солнечную ферму, так что вопросы хранения преобладают. Ветровая энергия занимает значительно больше земли (примерно в 50 раз), чем солнечная, поэтому перекачиваемые водохранилища не могут соперничать с площадью, предназначенной для ветряных электростанций.
Вариации и масштабирование
При исследовании потенциала гидроаккумулирования мы исходили из множества предположений. Легко упустить из виду выбор и последствия, которые он оказывает. Важен ли уклон 20% по бокам? Как все зависит от высоты плотины?
При общем анализе получается, что количество необходимых плотин пропорционально общему требуемому накоплению энергии, умноженному на боковой уклон ложбины (например, в %), умноженному на уклон ложбины, деленному на высоту плотину до четвертой мощности. Но интересно, что полных объема (и, следовательно, энергии), необходимых для бетона, зависят только от уклона полого пола, деленного на высоту плотины.
В результате одна 500-метровая плотина заменяет 16 250-метровых плотин, при этом затрачивается только половина общего количества бетона. Таким образом, масштабирование отдает предпочтение крупным проектам, а не мелким. Конечно, количество приемлемых площадок для мегапроектов может быть слишком маленьким, в то время как стремление найти в 16 раз больше меньших площадок — это не прогулка в парке.
Общая площадь озера масштабируется как обратная величина бокового уклона и обратная квадратная величина высоты плотины. Поэтому, естественно, из космоса будут более заметны более широкие и мелкие озера. Общий необходимый объем воды точно соответствует обратной высоте плотин.
Конечно, любая реальная реализация будет иметь широкий набор высот плотин. Я рассматриваю их всех одинаково, чтобы установить базовые цифры. Строгие средние значения не работают из-за нелинейного масштабирования, но это, по крайней мере, дает нам представление. Анализ, в котором я допускаю распределение высот плотин, будет просто пустой тратой моего и вашего времени.
Обычный трюк состоит в том, чтобы построить большую питательную трубу от нижней части верхней плотины до турбины/насоса, расположенной далеко внизу. Сделать это везде будет непросто, но дополнительные 500 м перепада улучшают 250-метровую плотину в 3,6 раза, а 500-метровую плотину — в 2,3 раза. Это уменьшает количество таких проектов, необходимых для аналогичного фактора (все еще большое количество). Но не слишком увлекайтесь этим вариантом: нам еще нужно место для установки нижнего резервуара. Если вы откажетесь от слишком большой высоты, у вас закончатся естественные стены и вертикальный рельеф, и потребуется очень большая площадь затопления для сбора воды.
Сравнение с реальными примерами
Гидроаккумулятор Ludington: 110 метров; 1,87 ГВт; 15 часов; 27 млн кВтч.
Хватит дурачиться. Давайте сравним эту страну фантазий с чем-то реальным. У нас есть 22 ГВт гидроаккумулирующих хранилищ в США, что составляет около 1 % от моей цели в 2 ТВт. Но они, как правило, являются спринтерами, а не марафонцами (обычно около 12 часов работы на полной мощности), поэтому фактическое хранилище не соответствует тому, что нам нужно, примерно в 1500 раз. Думаете, нам нужен только один день хранения? Все еще скидка в 200 раз.
Крупнейшая насосная гидроустановка в США (с точки зрения энергии, а не мощности) находится в Раккун-Маунтин, штат Теннесси. Я во многом обязан этому оборудованию своим комфортом с кондиционером в детстве. Водохранилище, расположенное на вершине горы, впадает в реку Теннесси на 300 м ниже (технически это водохранилище Никаджек). Установленная мощность составляет 1,532 ГВт, что предполагает расход 575 м³/с. Верхний резервуар обеспечивает необычно долгую работу в течение 22 часов, так что объем полезной воды составляет 45×10 6 м³, а запас энергии 34 млн кВтч. Площадь поверхности озера составляет 2,16 квадратных километров, в результате чего средняя глубина составляет 21 метр. (Земляная) плотина имеет высоту 70 м и длину 1800 м, из чего я рассчитал объем плотины около 10 6 м³ — примерно половину объема плотины Гувера.
Раккун-Маунтин: 302 м; 1,53 ГВт; 22 часа; 34 млн кВтч.
Что эти реальных чисел могут сказать мне о моей упрощенной геометрии и догадках, которые были введены? Основное отличие состоит в том, что геометрия Раккун-Маунтин имеет гораздо более пологие склоны: около 3–5% вверх по «лощине» и около 8% вверх по бокам. Нам потребуется 10 000 Раккун-Маунтинс, чтобы удовлетворить мои базовые энергетические возможности, хотя мы могли бы уменьшить мощность на единицу. Это становится 50 000, если вы не можете использовать трюк сброса в резервуар далеко внизу. Для 10 000 копий Енотовидной горы общая площадь озера (включая площадь озера внизу) примерно в три раза превышает размер озера Эри (размер озера Верхнее). Объем плотины составляет примерно одну пятую того, что мы имели раньше, и становится сопоставимым в той степени, в которой не используется трюк с глубоким падением. Общий объем секвестрированной воды в обоих случаях сравним (поскольку это всего мг/ч , а наша базовая линия имела ч = 250 м, в то время как Raccoon Mountain использует ч = 300 м).
Перепрофилирование гидроэлектростанции
Если в какой-то момент этого развития вы подумали: «Подождите минутку: зачем строить все эти гигантские плотины в горах, когда у нас уже есть большие озера и плотины, вода уже доставлена в порог?! тогда вы не одиноки: я задавался тем же вопросом.
Первое примечание: наша установленная мощность гидроэлектростанций в США составляет 78 ГВт; что в 25 раз меньше необходимой полной мощности.
Следующее замечание: расход воды не всегда доступен для реализации мощности установленной мощности. Например, гидроэлектростанции США производят около 270 миллиардов кВтч каждый год, что составляет всего 40% от того, что было бы выработано, если бы все плотины работали на 100% мощности круглый год. Например, годовая выработка плотины Гувера составляет 4,2 миллиарда кВтч, что составляет 23% от того, что установленная мощность в 2,08 ГВт может производить за год. Даже могучая Колумбия колеблется настолько, что плотина Гранд-Кули реализует только 35% своей мощности.
Эти точки важны, потому что для достижения необходимой выходной мощности в 2 ТВт нам нужно умножить гидроэнергетическую мощность потока на коэффициент 25 или коэффициент 60 больше, чем средний расход. Мы могли бы предсказать несколько проблем с эрозией здесь и там.
Все равно сделаем!
Не будем слабаками. Давайте просто нарастим наши гидроэлектростанции на освоенных участках и спросим, достаточно ли у нас накопителей энергии за плотинами. Один из способов взглянуть на это — выяснить, сколько энергии будет вырабатываться, если все озера, запруженные гидроэлектростанциями, опустятся на один метр за 24 часа. Вычисление этого для каждой плотины на основе площади поверхности каждого озера дает в общей сложности 170 ГВт мощности. Нам нужно больше, чем это. Наш спрос только на электроэнергию в этой стране составляет в среднем 450 ГВт, и, конечно, мы рассчитываем примерно в четыре раза больше, чтобы покрыть все наши потребности в энергии.
Получается, что для получения достаточного количества энергии из существующей инфраструктуры потребуется осушение каждого резервуара немногим более чем на 10 метров в день. Но по мере того, как озера высыхают, площадь поверхности сокращается, так что моя оценка в десять метров слишком мала. Кроме того, многие плотины выйдут из строя, как только мы выйдем за пределы 10-метрового диапазона, и тот факт, что подаваемая энергия падает по мере падения высоты воды, еще больше снижает пропускную способность. Используя объем, указанный за каждой плотиной, я обнаружил, что осушение всех водохранилищ за 7-дневный период обеспечивает мощность 500 ГВт. Конечно, плотины часто строятся последовательно вдоль реки, поэтому мы можем повторно использовать воду по пути. Это даст нам коэффициент в несколько раз и приблизит нас к нашей потребности.
Но давайте не будем забывать, что наш план здесь включает в себя опорожнение всех озер и рек водой, причем со скоростью, намного превышающей ту, которую обычно несут каналы. Это экстремальный маневр.
Осушить Великие озера
Пока мы «развлекаемся», давайте посмотрим, что мы можем получить из Великих озер. Верхние четыре озера находятся практически на одной высоте (перепад высоты от Верхнего до Эри — 6 метров), а между Эри и Онтарио перепад составляет 99 м. Мы называем это Ниагарским водопадом, хотя только половина водопада проходит поперек самого водопада.
Если бы мы осушили по одному метру из каждого верхнего озера, мы бы получили 54 миллиарда киловатт-часов энергии: примерно шестую часть запланированной мощности. Если проводить его в течение семи дней, поток составит 375 000 кубических метров в секунду, или в 125 раз больше нормального потока через водопад. Теперь я бы заплатил, чтобы увидеть это! Но сначала я хотел бы в последний раз посетить каждый город вдоль реки Святого Лаврентия.
Если бы мы попытались запереть воду в озере Онтарио, чтобы спасти тех, кто находится ниже по течению гнева, его уровень поднялся бы на 12 метров (39ноги). Осторожно, Торонто и Рочестер!
Труба, подающая эту воду к турбинам, должна иметь диаметр более 125 метров (или 160 трубок по 10 м в диаметре), чтобы ограничить скорость воды по трубам/турбинам ниже скорости автомагистрали! Как весело.
Я сошел с ума?
Почему я всегда так делаю: беру вызов и показываю, как нелепо решать проблему монолитным подходом? Может быть я это смешно!
Эта тенденция является отражением моего стремления понять, как мы можем столкнуться с огромными энергетическими проблемами впереди. Первым шагом всегда является оценка потенциал решения относительно полномасштабного спроса. Если он вытирает пол с избыточной мощностью, то отлично: это бесспорно простое решение. Если это не так, это тоже очень информативно.
Да, разнообразный портфель из полдюжины неадекватных решений может добавить адекватное решение. Но полдюжины прискорбно неадекватных решений не могут провернуть тот же трюк. До сих пор мои поиски продолжают находить прискорбно неадекватный тип. Масштаб замены ископаемого топлива настолько обескураживает , что мы очень быстро попадаем в неприятности, когда подставляем числа к предлагаемым решениям.
Распространенной реакцией на сообщение о батарее национального размера, особенно на форуме Oil Drum, было то, что я поступил глупо, рассматривая полномасштабную свинцово-кислотную батарею, и что перекачиваемое хранилище было более очевидным решением проблемы. Для меня это было неочевидно, но я еще не занимался математикой. Тот факт, что только одна из «маленьких» плотин, рассматриваемых здесь, содержит столько же бетона, сколько плотины «Три ущелья» и «Гранд-Кули» вместе взятые, унизительно. Я был бы впечатлен, если бы мы сделали один. Я был бы поражен, если бы мы сделали 25. И это всего лишь дает нам 1% от нашей потребности (или 7%, если вы все еще злитесь на 7-дневную батарею).
Достаточно ясно, что гидроаккумуляторы существуют и неплохо работают в определенных местах. Но демонстрация не подразумевает масштабируемости, и масштабирование существующих установок не дало радикально иного ответа (на самом деле потребовало еще установки на ). Огромный масштаб, который я вычисляю, означает, что простые коэффициенты два или даже десять здесь и там не меняют общего вкуса вывода.
Давайте проясним, что я не утверждаю, что крупномасштабное хранилище на уровне, который нам нужен, составляет невозможно . Но это гораздо более пугающе, чем кто-либо может себе представить. Это не вопрос «просто» наращивания, когда придет время. Мы могли бы легко оказаться плохо подготовленными и страдать от нехватки энергоресурсов, перебоев и длительного, медленного экономического спада, потому что мы коллективно не предвидели масштаба предстоящих проблем.