Гидравлический расчет трубопровода | Онлайн-калькулятор
Наш универсальный онлайн-калькулятор позволяет выполнить полный гидравлический расчет простого трубопровода, то есть определить гидравлическое сопротивление, потери напора по длине по всему участку или на 1 погонный метр, узнать средний расход воды. Расчет выполняется по принципу, описанному в СНиП 2.04.02-84 (СП 31.13330.2012) «Водоснабжение. Наружные сети и сооружения», более подробно с теорией можно ознакомиться ниже. Оптимальная скорость воды в трубе от 0.6 м/с до 1.5 м/с, максимальная – 3 м/с. Обращайте внимание на единицы измерения и материал трубопровода, это важно. Для того чтобы получить результат гидравлического расчета, корректно заполните поля калькулятора и нажмите кнопку «Рассчитать».
Смежные нормативные документы:
- СП 31.13330.2012 «Водоснабжение. Наружные сети и сооружения»
- СП 30.13330.2016 «Внутренний водопровод и канализация зданий»
- СП 60.
 13330.2016 «Отопление, вентиляция и кондиционирование воздуха»
13330.2016 «Отопление, вентиляция и кондиционирование воздуха» - ГОСТ 10705-80 «Трубы стальные электросварные»
- ГОСТ 9583-75 «Трубы чугунные, напорные, изготовленные методами центробежного и полунепрерывного литья»
- ГОСТ 539-80 «Трубы и муфты асбестоцементные напорные»
- ГОСТ 12586.0-83 «Трубы железобетонные напорные виброгидропрессованные»
- ГОСТ 16953-78 «Трубы железобетонные напорные центрифугированные»
- ГОСТ 18599-2001 «Трубы напорные из полиэтилена»
- ГОСТ 8894-86 «Трубы стеклянные и фасонные части к ним»
Теоретическое обоснование гидравлического расчета
Гидропотери в трубопроводах систем водоснабжения вызваны гидравлическим сопротивлениям труб, смежных стыковых соединений, арматуры и прочих соединительных элементов. Калькулятор выполняет расчет только для простого (прямого) трубопровода, поэтому для сложных систем рекомендуется совершать вычисления для каждого отдельного участка.
Согласно методике СП 31. 13330.2012 «Водоснабжение. Наружные сети и сооружения», гидравлический уклон (потери напора на единицу длины) определяется по формуле:
13330.2012 «Водоснабжение. Наружные сети и сооружения», гидравлический уклон (потери напора на единицу длины) определяется по формуле:
i = (λ / d) × (v2 / 2g)
- λ – коэффициент гидравлического сопротивления;
- d – внутренний диаметр труб, м;
- V – скорость воды, м/с;
- g – ускорение свободного падения, 9,81 м/с2.
Таким образом, из неизвестных остается только коэффициент гидравлического сопротивления, который рассчитывается по формуле:
λ = A1 × (A0 + C/V)m / dm
Коэффициенты А0, А1, С и значения показателя степени m соответствуют современным технологиям изготовления трубопроводов и принимаются согласно нижеуказанной таблицы. В случае, если эти параметры отличаются от перечисленных, производитель должен указывать их самостоятельно.
| Виды труб | m | A0 | A1 | С | |
| Новые стальные без внутреннего защитного покрытия или с битумным защитным покрытием | 0,226 | 1 | 0. 0159 0159 | 0.684 | |
| Новые чугунные без внутреннего защитного покрытия или с битумным защитным покрытием | 0,284 | 1 | 0.0144 | 2.360 | |
| Неновые стальные и неновые чугунные без внутреннего защитного покрытия или с битумным защитным покрытием | v < 1,2 м/с | 0,30 | 1 | 0.0179 | 0.867 |
| v ⩾ 1,2 м/с | 0,30 | 1 | 0.021 | 0.000 | |
| Асбестоцементные | 0,19 | 1 | 0.011 | 3.510 | |
| Железобетонные виброгидропрессованные | 0,19 | 1 | 0.01574 | 3.510 | |
| Железобетонные центрифугированные | 0,19 | 1 | 0.01385 | 3.510 | |
| Стальные и чугунные с внутренним пластмассовым или полимерцементным покрытием, нанесенным методом центрифугирования | 0,19 | 1 | 0.011 | 3.510 | |
| Стальные и чугунные с внутренним цементно-песчаным покрытием, нанесенным методом набрызга с последующим заглаживанием | 0,19 | 1 | 0. 01574 01574 | 3.510 | |
| Стальные и чугунные с внутренним цементно-песчаным покрытием, нанесенным методом центрифугирования | 0,19 | 1 | 0.01385 | 3.510 | |
| Пластмассовые | 0,226 | 0 | 0.01344 | 1.000 | |
| Стеклянные | 0,226 | 0 | 0.01461 | 1.000 | |
Расход воды в трубопроводе рассчитывается на основании известной усредненной скорости движения воды по трубе заданного сечения.
Q = π × (d2 / 4) × V / 1000
- d – внутренний диаметр трубопровода, мм;
- V – скорость потока жидкости, м/с.
Согласно СП 30.13330.2012 «Внутренний водопровод и канализация зданий» скорость движения воды в трубопроводах внутренних сетей не должна превышать 1.5 м/с, в трубопроводах хозяйственно-противопожарных и производственно-противопожарных систем – 3 м/с, в спринклерных и дренчерных системах – 10 м/с. Для большинства современных многоквартирных квартир и частных домов оптимальная скорость воды в трубе должна составлять от 0.6 м/с до 1.5 м/с.
Для большинства современных многоквартирных квартир и частных домов оптимальная скорость воды в трубе должна составлять от 0.6 м/с до 1.5 м/с.
Расчет коэффициента гидравлического сопротивления трения труб
03:32:27 - 21.02.2021
Онлайн калькулятор позволяет произвести расчет коэффициента гидравлического сопротивления трению трубопровода и определить потери давления при движении жидкости по трубопроводу.
| Расход жидкости | |
| Коэффициент кинематической вязкости ( для воды тем-рой 100C = 1,3, 200C = 1) |
|
| Диаметр трубопровода | |
| Длина трубопровода | |
| Плотность жидкости | |
| Коэффициент шероховатости стенок трубопровода | |
| Выберите тип трубопроводаЦельнотянутые (Латунь-Медь-Сталь)Цельнотянутые (Стальные новые)Цельнотянутые стальные(Б\У)Цельносварные стальныеКлепаные стальныеИз кровельной сталиОценкованые стальныеЧугунные новыеЧугунные водопроводыеЖелезобетонные новыеАсбстоцементныеСтеклянныеЖелезобетонные | |
Итог |
|
| Режим течения | |
| Скорость движения жидкости в трубопроводе, м/c | |
| Число Рейнольдса (Re) | |
| Коэффициент трения (λ) | |
| Коэффициент гидравлического сопротивления (ξ) | |
| Потеря давления (Δp), Па | |
Возврат к списку калькуляторов
| Аэродинамика | ||
| Массовый расход воздуха | – | ● |
| Объемный расход воздуха | – | ● |
| Подбор диаметра воздуховода | – | ● |
| Подбор размеров воздуховода | – | ● |
| Диаметр круглой диафрагмы | – | ● |
| Размеры прямоугольной диафрагмы | – | ● |
| Скорость воздуха по площади | – | ● |
| Расход воздуха по площади | – | ● |
| Скорость воздуха по диаметру воздуховода | ● | ● |
| Скорость воздуха по размерам воздуховода | ● | ● |
| Расход воздуха по диаметру воздуховода | ● | ● |
| Расход воздуха по размерам воздуховода | ● | ● |
| Потери давления на трение в круглом воздуховоде | ● | ● |
| Потери давления на трение в прямоугольном воздуховоде | ● | ● |
| Потери давления в местных сопротивлениях | ● | ● |
| Гидравлика | ||
Расход жидкости по мощности. Вода Вода | – | ● |
| Расход жидкости по мощности. Гликоль | – | ● |
| Мощность по диаметру трубопровода. Гликоль | – | ● |
| Мощность по расходу жидкости. Вода | – | ● |
| Мощность по расходу жидкости. Гликоль | – | ● |
| Подбор диаметра трубопровода по расходу жидкости | – | ● |
| Подбор диаметра трубопровода по мощности. Вода | – | ● |
| Подбор диаметра трубопровода по мощности. Гликоль | – | ● |
| Потери давления на трение в трубопроводе. Гликоль | – | ● |
| Потери давления в местных сопротивлениях. Гликоль | – | ● |
| Диаметр дросселирующей шайбы. Вода | – | ● |
| Kv клапана | – | ● |
| Изменение объема системы. Вода | – | ● |
| Изменение объема системы. Гликоль | – | ● |
| Тепловое удлинение трубопровода | – | ● |
| Скорость жидкости | ● | ● |
| Расход жидкости по диаметру трубопровода | ● | ● |
Мощность по диаметру трубопровода. Вода Вода | ● | ● |
| Потери давления на трение в трубопроводе. Вода | ● | ● |
| Потери давления в местных сопротивлениях. Вода | ● | ● |
| Потери давления на клапане | ● | ● |
| Отопление | ||
| Сопротивление теплопередаче ограждения из двух материалов | – | ● |
| Сопротивление теплопередаче ограждения из одного материала | ● | ● |
| Температура внутренней поверхности ограждения | ● | ● |
| Вентиляция | ||
| Мощность на охлаждение воздуха по температуре теплообменника | – | ● |
| Мощность на охлаждение воздуха по относительной влажности | – | ● |
| Мощность на охлаждение воздуха по энтальпии | – | ● |
| Мощность электродвигателя вентилятора | – | ● |
| Располагаемое давления естественной вентиляции | – | ● |
| Расход воды на пароувлажнение воздуха | – | ● |
| Мощность на пароувлажнение воздуха | – | ● |
| Мощность на нагрев воздуха | ● | ● |
| Расход воздуха по тепловыделениям | ● | ● |
| Расход воздуха по влаговыделениям | ● | ● |
| Свойства воздуха | ||
| Температура смеси воздуха | – | ● |
| Влагосодержание смеси воздуха | – | ● |
| Энтальпия смеси воздуха | – | ● |
| Относительная влажность смеси воздуха | – | ● |
| Давление насыщения пара по температуре | – | ● |
| Давление насыщения пара по влагосодержанию | – | ● |
| Барометрическое давление | – | ● |
| Парциальное давление | – | ● |
| Температура точки росы | – | ● |
| Плотность воздуха | – | ● |
| Удельная теплоёмкость воздуха | – | ● |
| Температура влажного термометра по относительной влажности | – | ● |
| Температура влажного термометра по энтальпии | – | ● |
| Влагосодержание воздуха по энтальпии | ● | ● |
| Влагосодержание воздуха по относительной влажности | ● | ● |
| Энтальпия воздуха по влагосодержанию | ● | ● |
| Энтальпия воздуха по относительной влажности | ● | ● |
| Относительная влажность воздуха по влагосодержанию | ● | ● |
| Относительная влажность воздуха по энтальпии | ● | ● |
| Свойства жидкости | ||
Температура замерзания. Гликоль Гликоль | ● | ● |
| Плотность. Вода | ● | ● |
| Плотность. Гликоль | ● | ● |
| Удельная теплоёмкость. Вода | ● | ● |
| Удельная теплоёмкость. Гликоль | ● | ● |
| Кинематическая вязкость. Вода | ● | ● |
| Кинематическая вязкость. Гликоль | ● | ● |
| Температура конденсации. Фреон | ● | ● |
| Температура кипения. Фреон | ● | ● |
| Давление конденсации. Фреон | ● | ● |
| Давление кипения. Фреон | ● | ● |
| Инженерная геометрия | ||
| Площадь изоляции покрытой по круглому сечению | – | ● |
| Площадь изоляции покрытой по прямоугольному сечению | – | ● |
| Эквивалентный диаметр | – | ● |
| Масса стального трубопровода | ● | ● |
| Площадь поверхности круглого воздуховода | ● | ● |
| Площадь поверхности прямоугольного воздуховода | ● | ● |
Онлайн калькулятор расчета скорости воды и газа в трубе
Автоматизированный расчет скорости движения потока в трубопроводе нашим калькулятором будет необходим в том случае, если Вы решили провести канализацию, отопительную или водопроводную систему своими руками в частном доме. Расчет поможет определиться в выборе диаметра трубы, его протяженности или количестве поворотов трубопровода.
Расчет поможет определиться в выборе диаметра трубы, его протяженности или количестве поворотов трубопровода.
Блок: 1/4 | Кол-во символов: 331
Источник: https://trubanet.ru/onlajjn-kalkulyatory/skorost-dvizheniya-zhidkosti-i-gaza-po-trube.html
на электронный журнал
New ToolBox Web
Units:
Блок: 2/2 | Кол-во символов: 134
Источник: https://www.tlv.com/global/RU/calculator/water-velocity-through-piping.html
Онлайн калькулятор для подсчета скорости воды и газа в трубопроводе
Рассчитать все параметры перемещения жидкости в водопроводной системе, вопреки кажущейся простоте, представляет собой сложную задачу, поскольку на поток воды действует одновременно множество разноречивых факторов.
Блок: 2/4 | Кол-во символов: 281
Источник: https://trubanet.ru/onlajjn-kalkulyatory/skorost-dvizheniya-zhidkosti-i-gaza-po-trube.html
Расчёт
Зависимость потери давления от диаметра трубы
В вашем броузере не работает html5
При расчете системы водоснабжения или отопления вы сталкиваетесь с задачей подбора диаметра трубопровода. Для решения такой задачи нужно сделать гидравлический расчет вашей системы, а для еще более простого решения – можно воспользоваться гидравлическим расчетом онлайн, что мы сейчас и сделаем.
Для решения такой задачи нужно сделать гидравлический расчет вашей системы, а для еще более простого решения – можно воспользоваться гидравлическим расчетом онлайн, что мы сейчас и сделаем.
Порядок работы:
1. Выберите подходящий метод расчета (расчет по таблицам Шевелева, теоретическая гидравлика или по СНиП 2.04.02-84)
2. Выберите материал трубопроводов
3. Задайте расчетный расход воды в трубопроводе
4. Задайте наружный диаметр и толщину стенки трубопровода
5. Задайте длину трубопровода
6. Задайте среднюю температуру воды
Результатом расчета будет график и приведенные ниже значения гидравлического расчета.
График состоит из двух значений (1 – потери напора воды, 2 – скорость воды). Оптимальные значения диаметра трубы будут написаны зеленым под графиком.
Т.е. вы должны задать диаметр так, чтобы точка на графике была строго над вашими зелеными значениями диаметра трубопровода, потому что только при таких значениях скорость воды и потери напора будут оптимальные.
Потери давления в трубопроводе показывают потерю давления на заданном участке трубопровода. Чем выше потери, тем больше придется совершить работы, чтобы доставить воду в нужное место.
Характеристика гидравлического сопротивления показывает, насколько эффективно подобран диаметр трубы в зависимости от потерь давления.
Для справки:
— если Вам необходимо узнать скорость жидкости/воздуха/газа в трубопроводе различного сечения – воспользуйтесь этим калькулятором
От автора:
Если данный гидравлический расчет трубопроводов был Вам полезен, то не забывайте делиться им с друзьями и коллегами.
Блок: 3/3 | Кол-во символов: 1786
Источник: https://prostobuild.ru/onlainraschet/244-gidravlicheskiy-raschet-truboprovoda-onlayn.html
Зачем нужен расчет
Каковы основные направления использования воды в здании? Их несколько:
- Потребление для санитарных, а также бытовых нужд.
- Устройство отопления с водяным теплоносителем.

- Водопровод системы пожаротушения.
- Система канализации стоков.
Каждое направление имеет свои особенности и характеристики по условиям эксплуатации. При недостаточной мощности трубопроводной системы возможно критично резкое снижение давления, а вероятность получения слабой струйки из пожарного шланга испортит настроение любому.
Скорость течения стоков по системе канализации также имеет особое значение, поскольку малейший просчет в угле наклона отрицательно сказывается на работе такого водопровода и его долговечности. Недостаточный угол предполагает возможность остановки действия, а излишний приводит к ускоренному засорению канала.
Блок: 3/4 | Кол-во символов: 817
Источник: https://trubanet.ru/onlajjn-kalkulyatory/skorost-dvizheniya-zhidkosti-i-gaza-po-trube.html
Влияние различных факторов на работу водопроводной сети
На первый взгляд механизм простой – есть магистраль с определенным диаметром и чем большего оно размера, тем больше пройдет по ней жидкости при определенном давлении.
Безусловно, это действенные факторы, влияющие на расход воды и интенсивность ее перемещения по водопроводной сети. Но это только начало длинного перечня, поскольку кроме них существуют и другие воздействия:
- Длина трубы. По мере перемещения жидкость испытывает обратное направлению потока воздействие от трения о стенки трубы. Величина сопротивления такова, что пренебречь ею невозможно. Разумеется, на консоли через сливное отверстие скорость истечения зависит только от давления. Но вытекшую жидкость нужно заместить, а быстрота ввиду сопротивления недостаточна.
- Прямое воздействие на скорость течения жидкости оказывает диаметр внутреннего сечения трубопровода. Чем он меньше, тем более сильное сопротивление потоку оказывается, поскольку площадь контакта по отношению к объему протекающей воды увеличивается. То есть, между этими параметрами существует обратно пропорциональная зависимость.
- Материал, из которого изготовлена круглая труба, также оказывает существенное влияние.
 Внутренняя поверхность пластиковых изделий, изготовленных из сшитого полиэтилена, более гладкая, чем у аналогичных из металла. Она оказывает гораздо меньшее сопротивление потоку. Более того, при расчете скорости жидкости в трубопроводе, изготовленном из металла, следует понимать, что он справедлив только для новой системы. Такие системы очень быстро засоряются известковыми отложениями на внутренних стенках и продуктами окисления металла. Учесть такие воздействия невозможно, поскольку интенсивность их накопления во многом зависит от качества воды. Величина сопротивления в новой трубе и засоренной может возрастать до 200 раз.
Внутренняя поверхность пластиковых изделий, изготовленных из сшитого полиэтилена, более гладкая, чем у аналогичных из металла. Она оказывает гораздо меньшее сопротивление потоку. Более того, при расчете скорости жидкости в трубопроводе, изготовленном из металла, следует понимать, что он справедлив только для новой системы. Такие системы очень быстро засоряются известковыми отложениями на внутренних стенках и продуктами окисления металла. Учесть такие воздействия невозможно, поскольку интенсивность их накопления во многом зависит от качества воды. Величина сопротивления в новой трубе и засоренной может возрастать до 200 раз. - Скорость движения жидкости в трубопроводной системе во многом зависит от ее сложность. Каждый поворот, каждый фитинг – это потеря скорости, причем степень влияния не ограничивается статистической погрешностью, а снижает проходимость многократно.
Учитывая сказанное, очевидно, что достоверно определить основные параметры действия водопровода гидравлическим расчетом практически невозможно. Тем не менее, расчет скорости воды в трубопроводе необходим для определения первичных данных по его основным характеристикам и делать его нужно с использованием калькулятора, используя режим online.
Тем не менее, расчет скорости воды в трубопроводе необходим для определения первичных данных по его основным характеристикам и делать его нужно с использованием калькулятора, используя режим online.
Блок: 4/4 | Кол-во символов: 2418
Источник: https://trubanet.ru/onlajjn-kalkulyatory/skorost-dvizheniya-zhidkosti-i-gaza-po-trube.html
Количество использованных доноров: 3
Информация по каждому донору:
- https://www.tlv.com/global/RU/calculator/water-velocity-through-piping.html: использовано 1 блоков из 2, кол-во символов 134 (2%)
- https://prostobuild.ru/onlainraschet/244-gidravlicheskiy-raschet-truboprovoda-onlayn.html: использовано 2 блоков из 3, кол-во символов 2231 (36%)
- https://trubanet.ru/onlajjn-kalkulyatory/skorost-dvizheniya-zhidkosti-i-gaza-po-trube.html: использовано 4 блоков из 4, кол-во символов 3847 (62%)
Программы расчета — ТЕХНОНИКОЛЬ
Калькуляторы онлайн
ТЕПЛОТЕХНИЧЕСКИЙ КАЛЬКУЛЯТОР С УЧЁТОМ НЕОДНОРОДНОСТЕЙ
С помощью данного онлайн калькулятора Вы сможете рассчитать необходимую толщину теплоизоляционного слоя, исходя из требуемого приведенного сопротивления теплопередаче для конкретного региона (города) и типа строительной системы с учетом термических неоднородностей конструкций.

ТЕХНИЧЕСКАЯ ИЗОЛЯЦИЯ
Данный расчет решает проблему выбора оптимальной толщины изоляции для энергосбережения. При расчете по нормам теплового потока толщина теплоизоляции определяется по ограничению плотности теплового потока через стенку трубопровода/резервуара.
КАЛЬКУЛЯТОР КЛИНОВИДНОЙ ТЕПЛОИЗОЛЯЦИИ
С помощью данного калькулятора Вы сможете рассчитать необходимое количество теплоизоляции для формирования основного и контруклона на плоской кровле.
КАЛЬКУЛЯТОР СКАТНОЙ КРОВЛИ PROF
Расчёт расхода кровельных материалов для скатной крыши.
ЗВУКОИЗОЛЯЦИОННЫЙ КАЛЬКУЛЯТОР
С помощью данного онлайн калькулятора Вы сможете подобрать систему звукоизоляции и рассчитать необходимую толщину звукоизоляционного слоя, исходя из требуемых индексов изоляции воздушного и ударного шума для конкретного региона (страны), типа здания и изолируемой конструкции, а также вида строительной системы.
КАЛЬКУЛЯТОР РАСХОДА ТЕПЛОВОЙ ЭНЕРГИИ
Расчет базового значения удельного расхода энергии на отопление согласно Приказу Министерства строительства и жилищно-коммунального хозяйства Российской Федерации №1550/пр от 17. 11.2017
11.2017
КАЛЬКУЛЯТОР РАСХОДА МАТЕРИАЛОВ КРОВЛИ ТЕХНОНИКОЛЬ. ВЕРСИЯ LITE
С помощью данного онлайн калькулятора Вы можете рассчитать необходимое количество материалов для устройства плоской кровли исходя из размеров кровли, ее уклона, района и требуемого сопротивления теплопередаче.
КАЛЬКУЛЯТОР СКАТНОЙ КРОВЛИ LITE
С помощью данного онлайн калькулятора Вы можете рассчитать необходимое количество материалов для устройства скатной кровли исходя из размеров кровли и ее уклона.
КАЛЬКУЛЯТОР РАСЧЁТА ВОДОСТОКА
С помощью данного онлайн калькулятора Вы можете рассчитать необходимое количество комплектации для устройства водосточной системы.
Библиотеки и надстройки
ALLPLAN
База Ассистентов (плоские кровли) Allplan
Файл ассистентов содержат 26 строительных систем плоских кровель компании ТехноНИКОЛЬ. Файл ассистентов разработан в 2012 версии Allplan.
Подробнее
Скачать
Спецификация материалов (плоские кровли) Allplan
Спецификации позволяют выполнить подсчет количества материалов плоских кровель ТехноНИКОЛЬ, по моделям из «Базы Ассистентов (плоские кровли) Allplan». Разработаны в 2012 версии Allplan.
Разработаны в 2012 версии Allplan.
Экспликации созданы в 2-х вариантах по ГОСТ, Форма 7.
Подробнее
Скачать
ARCHICAD
Библиотека реквизитов ArchiCAD
Файл реквизитов с расширением *.aat представляет собой библиотеку Многослойных конструкций, строительных материалов компании ТехноНИКОЛЬ и связанных с ними типов линий штриховок и пр.
Подробнее
Скачать
Каталог систем ArchiCAD
Файл каталога содержит строительные системы компании ТехноНИКОЛЬ: кровли, полы, фундаменты, тех. изоляцию и пр. Каталог выполнен в виде файла архивного проекта ArchiCAD (pla).
Подробнее
Скачать
AUTOCAD
Альбомы узлов AutoCADПерейти к подбору строительной системы ТехноНИКОЛЬ. Скачать узлы примыканий в формате DWG.
Подробнее
Динамические блоки AutoCAD
В дополнение к готовым альбомам узлов для разных типов систем (кровли, фасады, фундаменты и др. ) была разработана библиотека динамических блоков элементов узлов, которые используются в разработке данных альбомов.
) была разработана библиотека динамических блоков элементов узлов, которые используются в разработке данных альбомов.
Подробнее
Скачать
«Клин 2.0». Приложение для формирования уклонов на плоской кровле с помощью клиновидной изоляции
Программа КЛИН 2.0 разработана с целью ускорить проектирование систем клиновидной теплоизоляции с использованием систем КВ, XPS и ПИР производства ТехноНИКОЛЬ в среде AutoCAD.
Подробнее
Скачать
Приложение для расчета материалов скатных крыш
Основной функцией приложения является расчет количества материалов при устройстве скатных крыш с применением систем изоляции ТехноНИКОЛЬ с гибкой черепицей ТехноНИКОЛЬ SHINGLAS: ТН-ШИНГЛАС Классик и ТН-ШИНГЛАС Мансарда.
Подробнее
Скачать
RENGA
Каталог систем RengaФайл каталога содержит строительные системы компании ТехноНИКОЛЬ: кровли, полы, фундаменты, тех.
 изоляцию и пр. Каталог выполнен в виде файла архитектурного проекта Renga Architecture.
изоляцию и пр. Каталог выполнен в виде файла архитектурного проекта Renga Architecture.Подробнее
Скачать
REVIT
Библиотека материалов Revit
Библиотека насчитывает 147 строительных материалов, которые используются в создания многослойных конструкций (систем) ТехноНИКОЛЬ.
Расширение файла библиотеки «*adsklib».
Подробнее
Скачать
Каталог систем Revit
Представленный файл каталога содержит строительные системы ТехноНИКОЛЬ крыш, полов, фундаментов, фасадов и технической изоляции в виде семейств, соответствующих категорий.
Каталог создан на стандартном шаблоне, поставляемым с установкой Revit. Версия файла — Revit 2016.
Подробнее
Скачать
Альбомы узлов Revit
Альбом узлов ТехноНИКОЛЬ включает 200 узлов примыканий для 39 строительных систем. Альбом создан в стандартном шаблоне Revit. Версии файлов – 2016/ 2017/ 2018/ 2019. Узлы созданы при помощи семейств элементов узлов.
Версии файлов – 2016/ 2017/ 2018/ 2019. Узлы созданы при помощи семейств элементов узлов.
Подробнее
Скачать
Комплектующие для плоской кровли Revit
Библиотека комплектующих включает в себя модели водоприемных воронок внутреннего водостока, парапетных воронок, аэраторов, пешеходных дорожек и прочих элементов.
Подробнее
Скачать
Клин ТехноНИКОЛЬ
Клин ТехноНИКОЛЬ — это программная надстройка для Revit, предназначенная для создания уклонов на плоской кровле с помощью клиновидной теплоизоляции.
Так же приложение содержит каталог плоских кровель, выноску многослойных конструкций по ГОСТ и дополнительные инструменты для работы с конструкциями кровель.
Подробнее
Скачать
SKETCHUP
Каталог систем SketchUpФайл каталога содержит строительные системы компании ТехноНИКОЛЬ: кровли, полы, фундаменты, фасады и узлы примыканий.
 Каталог выполнен в виде файла архивного проекта LayOut for SketchUp 2018 (layout).
Каталог выполнен в виде файла архивного проекта LayOut for SketchUp 2018 (layout).Подробнее
Скачать
Расчет потерь напора в трубопроводах
В процессе течения нефтепродуктов имеют место потери напора на трение hτ и местные сопротивления hMC.
Потери напора на трение при течении ньютоновских жидкостей в круглых трубах определяются по формуле Дарси—Вейсбаха
где λ — коэффициент гидравлического сопротивления; L, D — соответственно длина и внутренний диаметр трубопровода; W — средняя скорость перекачки; g — ускорение силы тяжести.
Величина коэффициента гидравлического сопротивления λ в общем случае зависит от числа Рейнольдса Re = W • D/v и относительной шероховатости труб ε = kэ/D (здесь v — кинематическая вязкость нефтепродукта при температуре перекачки; кэ — эквивалентная шероховатость стенки трубы).
При ламинарном режиме перекачки (Re = ReKp) расчет λ выполняется по формуле Стокса
В переходной зоне (ReKp < Re < Rerp) расчет λ наиболее точно может быть выполнен по формуле Гипротрубопровода
Эквивалентная шероховатость kэ стальных труб
В зоне гидравлически гладких труб турбулентного режима (ReKp < Re < Rel) расчет λ выполняется по формуле Блазиуса
Для расчета λ в зоне смешанного трения турбулентного режима (ReI < Re = ReII) наиболее часто используется формула Альтшуля
В зоне квадратичного трения турбулентного режима (Re > ReII) расчет λ обычно ведут по формуле Шифринсона
Нетрудно видеть, что формулы Стокса, Блазиуса и Шифринсона могут быть представлены зависимостью одного вида
где А, т — коэффициенты, величина которых для каждой зоны трения неизменна.
Однако формула Альтшуля к этому виду не приводится. Это исключает возможность решения гидравлических задач в общем виде.
Ту же задачу можно было решить следующим образом. При Re = ReI еще справедлива формула Блазиуса, а при Re = RеI уже можно пользоваться формулой Шифринсона. Учитывая, что переходные числа Рейнольдса Альтшулем рекомендовано находить по формулам:
ReI=10/ε; ReII=500/ε.
для зоны смешанного трения получаем:
Поделив почленно получим:
откуда
Различие в выражениях для расчета коэффициента А объясняется тем, что в первом случае не было сделано необходимое алгебраическое преобразование
Среднеквадратичная погрешность аппроксимации В.ДБелоусова по сравнению с формулой Альтшуля составляет около 5%. Связано это, в частности, с тем, что ее автор не стремился сделать погрешность вычислений минимальной, а исходил из условия равенства коэффициентов X на границах зоны смешанного трения и соседних зон.
Автору совместно с аспиранткой Н.В. Морозовой удалось свести уравнение Альтшуля к виду со среднеквадратичной погрешностью 2,6%. Это было сделано следующим образом.
Представим формулу Альтшуля в виде
Недостатком данной записи является то, что расчетный коэффициент 0,11(68 + ε · Re) °-25 является функцией числа Рейнольдса. Вместе с тем из формул следует, что в зоне смешанного трения справедливо неравенство
10 < ε · Re < 500.
Задаваясь значениями г • Re в этом диапазоне, сначала рассчитали величины функции 0,11(68 + ε · Re)0’26, а затем, используя метод наименьших квадратов, заново описали полученные точки выражением 0,206( ε · Re)0’15.
Подставив его получили искомую зависимость
Из нее видно, что в зоне смешанного трения турбулентного режима величины коэффициентов А и т равны 0,206 • е0,15 и 0,1 соответственно. Среднеквадратичная погрешность расчетов по формуле относительно формулы Альтшуля — менее 3%, что меньше, чем по другим известным аппроксимациям.
Следует подчеркнуть, что учет наличия переходной зоны приводит к изменению критического числа Рейнольдса. Кроме того, А.Д. Альтшуль, строго говоря, для переходных чисел Рейнольдса рекомендует диапазоны
Чтобы уточнить величины Reкр, ReI ReII и найти величину Re.x,, воспользуемся следующим способом. При Re = ReKp еще справедлива формула Стокса» но в то же время уже справедлива формула Гипротрубопровода. То есть можно составить уравнение
Освобождаясь от знаменателя, получаем квадратное уравнение 0,16-10-4 · Reкр-13 · 10-4 · Reкp-64 = 0, единственным положительным корнем которого является Reкp~2040.
Рассуждая аналогично, можно найти все остальные характерные числа Рейнольдса. Приравняв формулы Гипротрубопровода и Блазиуса, получаем Reкp = 2800. Из равенства правых частей формулы Блазиуса и формулы находим, что ReI = 17,5/ε. Наконец, приравняв правые части формулы и формулы Шифринсона, несложно найти, что ReII = 531/ε.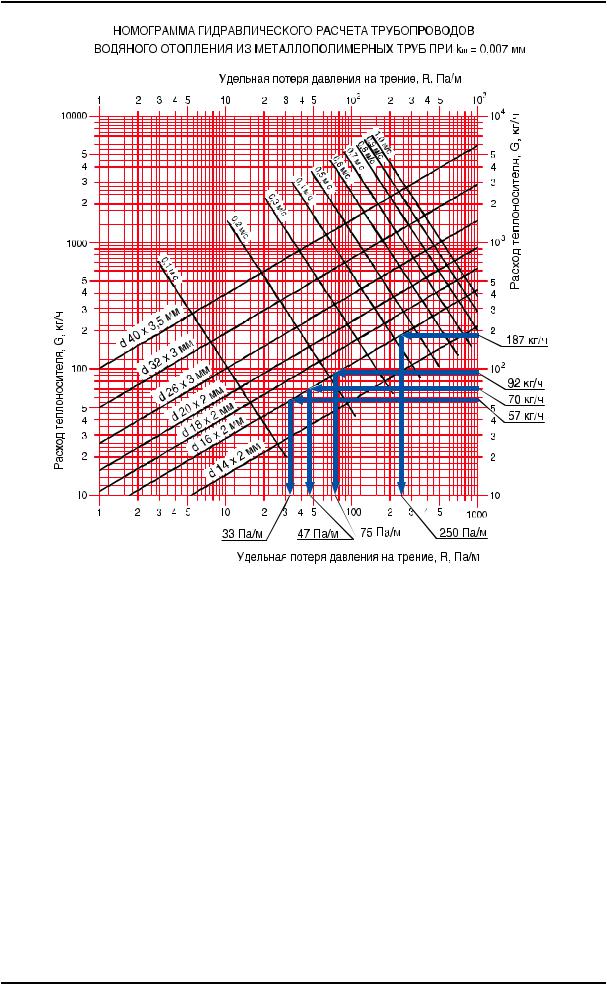
В тех случаях, когда необходимо, чтобы зависимость потерь напора на трение от расхода Q была выражена в явном виде, удобно использовать обобщенную формулу Лейбензона
где β — расчетный коэффициент, равный
Формула получается подстановкой выражения в формулу Дарси—Вейсбаха .
Учитывая, что формулу Гипротрубопровода можно привести к виду
Рекомендуемые величины коэффициентов А, β и m
Для вычисления потерь напора на трение при течении нефтепродуктов, проявляющих вязкопластичные свойства, можно воспользоваться уравнением Букингема (в виде аппроксимации, полученной проф. В.Е. Губиным)
где ΔР — перепад давления при течении вязкопластичной жидкости со средней скоростью W в трубопроводе диаметром D и длиной L; η — пластическая вязкость; F(И) — расчетная функция
где И — число Ильюшина
Потери напора на местные сопротивления
Данный вид потерь напора определяется по формуле Вейсбаха
где ξ — коэффициент местного сопротивления.
Величина коэффициента ξ, зависит от вида местного сопротивления и режима течения.
При ламинарном режиме течения величину коэффициента местного сопротивления следует вычислять по формуле
где ξг — коэффициент местного сопротивления при турбулентном режиме; А2 — постоянный коэффициент.
Коэффициенты местных сопротивлений при турбулентном режиме течения
Вид местного сопротивления | А2 | ξг |
Чялвижка открытая: | ||
— на 100% | 75 | 0,15 |
— на 75% | 350 | 0,20 |
— на 50% | 1300 | 2,00 |
— на 25% | 3000 | 20,0 |
Вентиль стандартный: | ||
— Dv = 80-100 мм | 3000 | 4,0 |
— Dy = 150-200 мм | — | 4,7 |
— Dy. | 5000 | 5,3 |
Обратный клапан: | ||
— Dy80-100 мм | — | 8,0 |
— Dy150-200 мм | — | 4,0 |
— Dy = 250-300 мм | — | 2,0 |
Компенсатор сальниковый | — | 0,2 |
Компенсатор П-образный: | ||
— Dy= 50-100 мм | 5000 | 2,2 |
— Dy = 200-300 мм | — | 2,4 |
— Dy = 400-500 мм | — | 2,8 |
Фильто для нефтепродуктов: | ||
— светлых | — | 1,70 |
— темных | — | 2,20 |
Калькулятор расчета характеристик кольцевого сечения (трубы)
- Подробности
Калькулятор онлайн рассчитывает геометрические характеристики (площадь, моменты инерции, моменты сопротивления изгибу, радиусы инерции) плоского сечения в виде кольца (трубы) по известным линейным размерам и выводит подробное решение.
| Исходные данные: | ||
| Наружный диаметр d, мм | ||
| Толщина стенки s, мм | ||
| Определение вспомогательных данных: | ||
| Внутренний диаметр d1, мм | расчет внутреннего диаметра кольца | |
| Решение: | ||
| Площадь сечения, мм2 | расчет площади сечения кольца | |
| Осевые моменты инерции относительно центральных осей, мм4 | расчет момента инерции кольца относительно оси ОХ расчет момента инерции кольца относительно оси ОY | |
| Моменты сопротивления изгибу, мм3 | расчет момента сопротивления изгибу кольца относительно оси ОХ расчет момента сопротивления изгибу кольца относительно оси ОY | |
| Радиусы инерции сечения, мм | расчет радиуса инерции кольца относительно оси ОХ расчет радиуса инерции кольца относительно оси ОY | |
Помощь на развитие проекта premierdevelopment. ru
ru
Спасибо, что не прошели мимо!
I. Порядок действий при расчете характеристик кольцевого сечения (трубы):
- Для проведения расчета требуется ввести наружный диаметр сечения d и толщину стенки s.
- По введенным данным программа автоматически вычисляет внутренний диаметр сечения d1.
- Результаты расчета площади, моментов сопротивления изгибу, моментов и радиусов инерции кольцевого сечения выводятся автоматически.
- На рисунке справа приведены необходимые размеры элементов сечения.
II. Примечание:
- Блок исходных данных выделен желтым цветом, блок промежуточных вычислений выделен голубым цветом, блок решения выделен зеленым цветом.
Онлайн калькулятор: Толщина стенки трубы
Толщина стенки трубы
Формула Барлоу используется для расчета давления в трубе с учетом ее диаметра, толщины стенки и кольцевого напряжения (в материале трубы). Таким образом, его можно использовать для вычисления любого из этих параметров как функции трех других.
Таким образом, его можно использовать для вычисления любого из этих параметров как функции трех других.
Помимо некоторых других упрощений, важное теоретическое допущение, сделанное для использования формулы Барлоу, состоит в том, что стенка трубы ведет себя как мембрана (или тонкостенная труба), что означает, что кольцевое напряжение в стенке трубы распределяется равномерно по всем его толщина.Внутри стенки трубы отсутствуют моменты любого типа. Одним из параметров, обеспечивающих поведение мембраны в стенке трубы, является отношение диаметра к толщине (D / t), которое должно быть больше или равно 20 , хотя некоторые авторы считают 16 .
Однако решение о том, использовать ли формулу или нет, обычно основывается не на геометрии ее сечения (отношение D / t), а на обслуживании трубы, с учетом типа жидкости, промышленности и физических условий, таких как, например, , ASME (Американская ассоциация инженеров-механиков) делает.
- P: Давление в трубе
- S: Обруч
- т: Толщина стенки трубы
- D: Внешний диаметр
Расчеты по формуле Барлоу
Точность расчетовЦифры после десятичной точки: 3
content_copy Ссылка сохранить Сохранить расширение Виджет
Следуя этим критериям обслуживания, код ASME B31. 4 (Трубопроводные системы транспортировки жидкостей и шламов) применяет формулу следующим образом:
4 (Трубопроводные системы транспортировки жидкостей и шламов) применяет формулу следующим образом:
- A: Допуск на резьбу, нарезание канавок, коррозию
Толщина стенки по формуле Барлоу согласно ASME B31.4
Точность расчетаЦифры после десятичной точки: 3
Толщина стенки трубы, (дюймы)
content_copy Ссылка сохранить Сохранить расширение Виджет
КодASME B31.8 (Системы газопроводов и газопроводов) применяет его следующим образом:
и для расчета минимальной толщины стенки с учетом припуска:
это должно быть выражено так:
- F: Расчетный коэффициент
- E: Коэффициент продольного соединения
- T: Температурный коэффициент снижения номинальных характеристик
- A: Допуск на резьбу, нарезание канавок, коррозию
Давление в трубе по формуле Барлоу согласно ASME B31.8
Расчетный коэффициент, (безразмерный) 0,80 для Класса размещения 1, Раздела 10,72 для Класса местоположения 1, Раздела 20. 60 для Класса местоположения 20,50 для Класса местоположения 30,40 для Класса размещения 4 Коэффициент продольного соединения (безразмерный) 1,00 для Бесшовные трубы ASTM A531. 00 для трубы, сваренной сопротивлением ASTM A53 0,60 для трубы ASTM A53, сваренной встык: труба непрерывного шва 1,00 для трубы ASTM A106 бесшовная 0,80 для трубы электросварной сварки плавлением ASTM A134 1,00 для трубы электросварной сварки ASTM A135 0.60 для трубы API 5L, сваренной встык с печью, 0,80 для трубы, сваренной встык, ASTM A1390,80 для трубы ASTM A211, сваренной спиральной сваркой, 1,00 для бесшовной трубы ASTM A333 1,0 для трубы, сваренной сопротивлением ASTM A333 Дуговая сварная труба 0,80 для электросварной сварки ASTM A671 классов 13,23,33,43,53 Труба 1,00 для электросварки плавлением ASTM A671 классов 12,22,32,42,52 Труба0,80 для электросварной сварки ASTM A672 Классы 13,23,33,43,53 pipe1.0 для ASTM A672, сваренные электросваркой плавлением классов 12,22,32,42,52 pipe1.00 для бесшовной трубы API 5L 1,00 для трубы электросварной сварки API 5L 1,00 для трубы API 5L, сваренной оплавлением оплавлением 1,00 для трубы API 5L, полученной дуговой сваркой под флюсом Температурный коэффициент, (безразмерный) 1,000 (для 250 ºF или менее) 0,967 ( для 300 ° F) 0,933 (для 350 ° F) 0,900 (для 400 ° F) 0,867 (для 450 ° F) Точность вычисления
60 для Класса местоположения 20,50 для Класса местоположения 30,40 для Класса размещения 4 Коэффициент продольного соединения (безразмерный) 1,00 для Бесшовные трубы ASTM A531. 00 для трубы, сваренной сопротивлением ASTM A53 0,60 для трубы ASTM A53, сваренной встык: труба непрерывного шва 1,00 для трубы ASTM A106 бесшовная 0,80 для трубы электросварной сварки плавлением ASTM A134 1,00 для трубы электросварной сварки ASTM A135 0.60 для трубы API 5L, сваренной встык с печью, 0,80 для трубы, сваренной встык, ASTM A1390,80 для трубы ASTM A211, сваренной спиральной сваркой, 1,00 для бесшовной трубы ASTM A333 1,0 для трубы, сваренной сопротивлением ASTM A333 Дуговая сварная труба 0,80 для электросварной сварки ASTM A671 классов 13,23,33,43,53 Труба 1,00 для электросварки плавлением ASTM A671 классов 12,22,32,42,52 Труба0,80 для электросварной сварки ASTM A672 Классы 13,23,33,43,53 pipe1.0 для ASTM A672, сваренные электросваркой плавлением классов 12,22,32,42,52 pipe1.00 для бесшовной трубы API 5L 1,00 для трубы электросварной сварки API 5L 1,00 для трубы API 5L, сваренной оплавлением оплавлением 1,00 для трубы API 5L, полученной дуговой сваркой под флюсом Температурный коэффициент, (безразмерный) 1,000 (для 250 ºF или менее) 0,967 ( для 300 ° F) 0,933 (для 350 ° F) 0,900 (для 400 ° F) 0,867 (для 450 ° F) Точность вычисленияЦифры после десятичной точки: 3
content_copy Ссылка сохранить Сохранить расширение Виджет
Код ASME B31.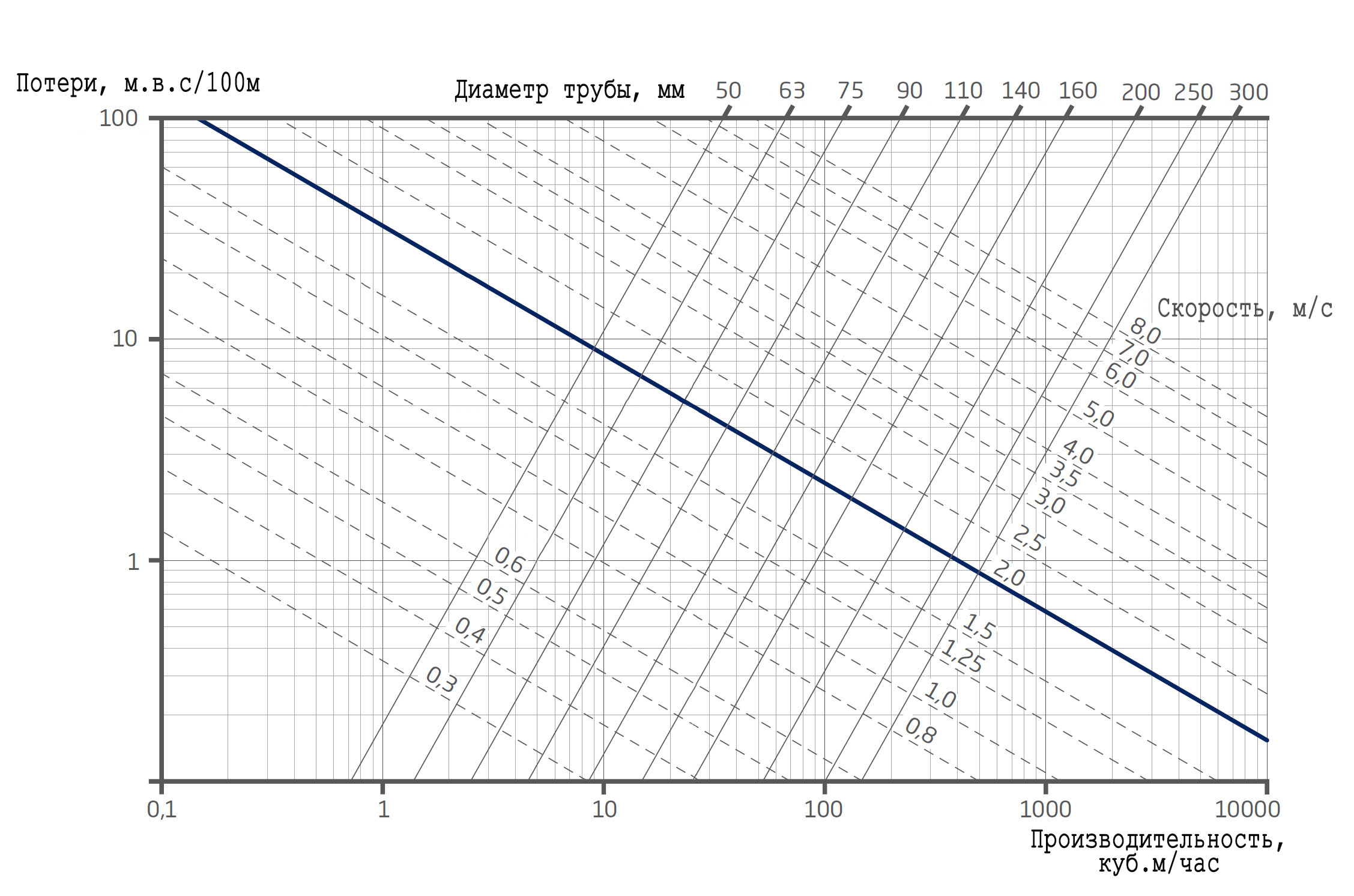 9 (Строительные трубопроводы) применяет его следующим образом:
9 (Строительные трубопроводы) применяет его следующим образом:
- E: Коэффициент продольного соединения
- A: Допуск на резьбу, нарезание канавок, коррозию
Толщина стенки трубы по формуле Барлоу согласно ASME B31.9
Коэффициент продольного соединения, (безразмерный) 0,6 (для трубы под сварку встык или непрерывной сварки) 0,75 (для трубы со спиральным соединением ASTM A211) 0,8 (для трубы с одинарным стыковым сварным швом) 0,85 (для трубы с контактным сварным швом) 0,9 (для трубы с двойным труба под сварку встык) 1,00 (для стыкового шва со 100% радиографическим исследованием трубы) Точность расчетаЦифры после десятичной точки: 3
Толщина стенки трубы, (дюймы)
content_copy Ссылка сохранить Сохранить расширение Виджет
С другой стороны, в отличие от предположения о тонкой стенке или теории мембран, существуют формулы для изогнутой пластины или толстостенной трубы, полученные из теории Ламе, использование которых более сложно, иногда с итерациями, и требует осторожного подхода, например, например, в ASME B 31. 1 (силовой трубопровод), код ASME B 31.3 (технологический трубопровод) и ASME B 31.5 (холодильный трубопровод и компоненты теплопередачи).
1 (силовой трубопровод), код ASME B 31.3 (технологический трубопровод) и ASME B 31.5 (холодильный трубопровод и компоненты теплопередачи).
Сжатый воздух — потеря давления в трубопроводах
Падение давления в трубопроводах сжатого воздуха можно рассчитать с помощью эмпирической формулы
dp = 7,57 q 1,85 L 10 4 / (d 5 p) ( 1)
, где
dp = падение давления (кг / см 2 )
q = объемный расход воздуха при атмосферных условиях (FAD) (м 3 ) / мин)
L = длина трубы (м)
d = внутренний диаметр трубы (мм)
p = начальное давление по манометру (кг / см 2 )
- 1 кг / см 2 = 98068 Па = 0.98 бар = 0,97 атмосферы = 736 мм рт. Ст. = 10000 мм H 2 O = 10 м H 2 O = 2050 фунтов на кв.
 O
O
Примечание! — давление — это «сила на единицу площади», и обычно используемые единицы давления, такие как кг / см 2 и аналогичные, в принципе неверны, поскольку кг является единицей массы. Массу нужно умножить на силу тяжести г , чтобы получить силу (вес).
Сжатый воздух — Номограмма падения давления
Номограмма ниже может использоваться для оценки падения давления в трубопроводах сжатого воздуха с давлением 7 бар (100 фунтов на кв. Дюйм).
Онлайн-калькулятор падения давления в трубопроводе сжатого воздуха — метрические единицы
Калькулятор ниже можно использовать для расчета падения давления в трубопроводах сжатого воздуха.
Онлайн-калькулятор падения давления в трубопроводе сжатого воздуха — британские единицы
Калькулятор, представленный ниже, можно использовать для расчета падения давления в трубопроводах сжатого воздуха.
ВНИМАНИЕ! — перепад давления выше 1 кг / см 2 (14-15 фунтов на кв. Дюйм) в общем случае не имеет значения, а приведенные выше формулы и калькуляторы могут быть недействительными.
Дюйм) в общем случае не имеет значения, а приведенные выше формулы и калькуляторы могут быть недействительными.
Для более точного расчета — или для более длинных трубопроводов с большими перепадами давления — разделите линию на части и рассчитайте перепад давления и конечное давление для каждой части. Используйте конечное давление в качестве начального давления для следующих частей. Конечное давление после последней части — это конечное давление в конце трубопровода. Падение давления для всего трубопровода также можно рассчитать путем суммирования падений давления для каждой части.
Таблица падения давления в трубопроводе сжатого воздуха
С помощью этой таблицы Excel (в метрических единицах измерения) можно выполнить расчеты для других давлений и / или длин труб.
Одна и та же таблица, включая различные типы труб (британские единицы).
Или, как вариант — Трубопроводы сжатого воздуха — Расчет падения давления — в Google Docs. Вы можете открывать, сохранять и изменять свою собственную копию электронной таблицы Google, если вы вошли в свою учетную запись Google.
Таблица падения давления в трубопроводе сжатого воздуха — начальное манометрическое давление
7 кг / см 2 (100 фунтов на кв. Дюйм)Падение давления в 100 м (330 футов) график сжатого воздуха 40 стальных трубопроводов указаны в таблицах внизу:
Падение давления в трубопроводной арматуре и клапанах
Обсуждение эквивалентной длины (L
e / D), коэффициента сопротивления (K) и коэффициента расхода клапана (C v ) Методы Авторские права © Харви Уилсон — Katmar Software
Октябрь 2012 г.
Если вам нужен калькулятор для расчета размеров труб и расчетов падения давления, перейдите на страницу AioFlo.
Содержание
1. Введение
Размер труб для оптимальной экономии требует, чтобы инженеры могли точно рассчитать расход и падение давления в этих трубах. Цель этого документа — обсудить различные доступные методы для поддержки этих расчетов. Основное внимание будет уделено методам расчета малых потерь при определении размеров труб и, в частности, рассмотрению следующих аспектов:
- преимущества и недостатки каждого метода
- Число Рейнольдса и режим течения (турбулентный против ламинарного)
- примерочный размер
- Шероховатость фитинга
- Шероховатость присоединенного трубопровода
- преобразование данных из одного метода в другой
2.Фон
За прошедшие годы был достигнут значительный прогресс в разработке методов определения падения давления при течении жидкости по прямым трубам. Точные процедуры определения размеров труб необходимы для достижения экономического оптимума за счет баланса капитальных и эксплуатационных затрат. Промышленность сошлась на методе Дарси-Вайсбаха, который удивительно прост, учитывая охват охватываемых им областей применения.
Формула Дарси-Вайсбаха обычно используется в следующей форме:
Уравнение (1) выражает потерю давления из-за трения в трубе как напор (h L ) текущей жидкости.
Термины и размеры в уравнении (1):
h L напор жидкости, размер равен длине
ƒ Коэффициент трения Муди (также называемый коэффициентом трения Дарси-Вайсбаха), безразмерный
L Длина прямой трубы, размер равен длине
Dinside диаметр трубы, размер — длина
средняя скорость жидкости (объемный расход / площадь поперечного сечения), размер — длина / время
ускорение под действием силы тяжести земли, размер — длина / время 2
Размеры в уравнении (1) могут быть в любом согласованном наборе единиц.Если коэффициент трения Фаннинга используется вместо коэффициента трения Муди, тогда ƒ необходимо заменить на 4ƒ.
В длинных трубопроводах большая часть падения давления происходит из-за трения в прямой трубе, а падение давления, вызванное фитингами и клапанами, называется «незначительной потерей». По мере того, как трубы становятся короче и сложнее, доля потерь, связанных с фитингами и клапанами, увеличивается, но по традиции они все еще называются «незначительными потерями».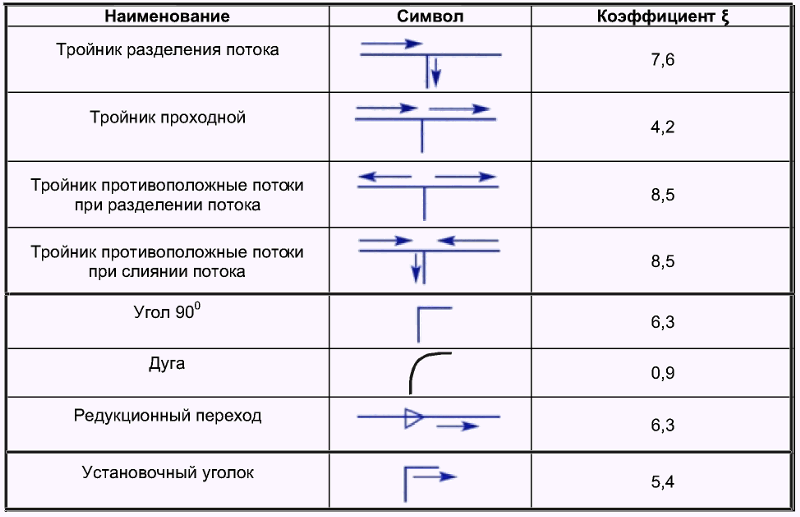
За последние несколько десятилетий был достигнут значительный прогресс в точном определении малых потерь, но на данный момент они не могут быть определены с той же степенью точности, что и большие потери, вызванные трением в прямой трубе.Эта ситуация усугубляется тем фактом, что эти недавние разработки еще не проникли на все уровни инженерии, и существует множество старых документов и текстов, в которых используются более старые и менее точные методы. Среди инженеров по-прежнему существует значительная путаница в том, какие методы лучше всего использовать и даже как их использовать.
К сожалению, один из наиболее широко используемых и уважаемых текстов, сыгравший важную роль в продвижении современного уровня техники, усугубил эту путаницу, включив ошибки и плохо сформулированные описания.(См. Раздел 4 ниже)
Тем не менее, используя имеющиеся в настоящее время знания и проявляя осторожность, незначительные потери могут быть определены с более чем достаточной точностью во всех ситуациях, кроме самых критических.
3. Три метода определения мелких убытков
Три метода, которые используются для расчета малых потерь при определении размеров труб, — это эквивалентная длина (L e / D), коэффициент сопротивления (K) и коэффициент расхода клапана (C v ), хотя C Метод v почти исключительно используется для клапанов.Еще больше усложняет ситуацию то, что метод коэффициента сопротивления (K) имеет несколько уровней уточнения, и при использовании этой процедуры важно понимать, как было определено значение K, и диапазон его применимости. Также существует несколько определений для C v , и они обсуждаются ниже.
Для всех трубопроводных фитингов обнаружено, что потери близки к величине, пропорциональной второму члену в уравнении (1). Этот термин (v 2 / 2g) известен как «скоростной напор».Таким образом, метод эквивалентной длины (L e / D) и коэффициент сопротивления (K) нацелен на поиск правильного множителя для члена скоростного напора.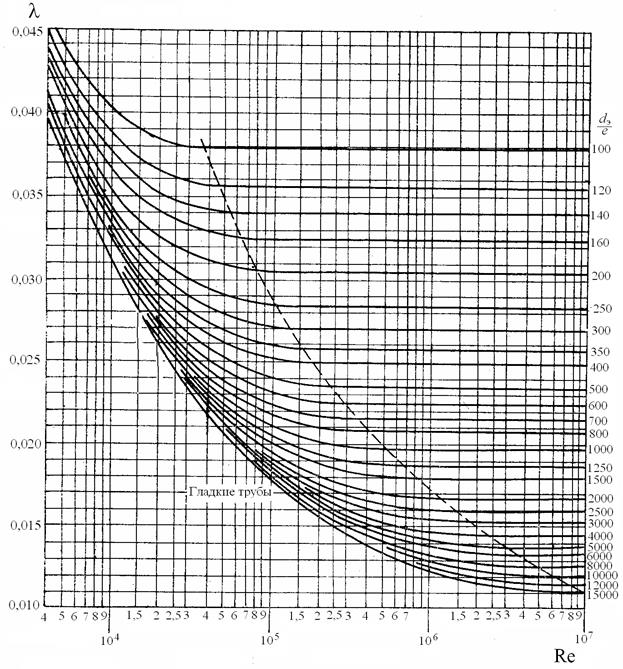
3.1 Метод эквивалентной длины (L e / D)
Этот метод основан на наблюдении, что основные потери также пропорциональны скоростному напору. Метод L e / D просто увеличивает коэффициент умножения в уравнении (1) (т.е. ƒL / D) на длину прямой трубы (например, L e ), что приводит к падению давления, эквивалентному потерям в арматура, отсюда и название «эквивалентная длина».Таким образом, коэффициент умножения становится ƒ (L + L e ) / D.
На ранних стадиях проектирования, когда не определена точная трасса трубопровода, эквивалентная длина может быть оценена как допуск на широкую щетку, например «добавить 15% к прямой длине, чтобы покрыть фитинги». Однако, если проект завершен и доступна подробная разборка фитингов, возможен более точный расчет малых потерь за счет использования экспериментально определенных эквивалентных длин для каждой из фитингов и клапанов.
Экспериментально было обнаружено, что если эквивалентные длины для диапазона размеров данного типа фитинга (например, изгиба с большим радиусом 90) разделить на диаметры фитингов, то получится почти постоянное соотношение (например, L e / D). Это очень упрощает табулирование данных эквивалентной длины, поскольку одного значения данных достаточно для покрытия всех размеров этого фитинга. Некоторые типичные данные для нескольких часто используемых фитингов приведены в таблице ниже:
Это очень упрощает табулирование данных эквивалентной длины, поскольку одного значения данных достаточно для покрытия всех размеров этого фитинга. Некоторые типичные данные для нескольких часто используемых фитингов приведены в таблице ниже:
| Тип фитинга | L e / D |
|---|---|
| Задвижка, полностью открытая | 8 |
| Кран шаровой полнопроходной | 3 |
| Шаровой кран, уменьшенное отверстие | 25 |
| Запорный клапан, полностью открытый | 320 |
| 90 отвод с резьбой | 30 |
| Колено с большим радиусом 90 | 13 |
| 45 отвод с резьбой | 16 |
| Колено с большим радиусом 45 | 10 |
| Тройник приварной проходной | 10 |
| Тройник сварной проходной | 60 |
Таблица эквивалентных длин для трубных фитингов
(чистая стальная труба промышленного назначения)
Эти данные предназначены только для иллюстрации и не являются исчерпывающими. Подробные таблицы значений эквивалентной длины для стальных и пластиковых труб доступны в другой нашей статье.
Подробные таблицы значений эквивалентной длины для стальных и пластиковых труб доступны в другой нашей статье.
Обратите внимание, что эта случайная ситуация с постоянным L e / D для всех размеров не применима к некоторым фитингам, таким как входы и выходы, а также к фитингам, таким как изменения диаметра и отверстий — оба из которых включают более одного отверстия. размер.
Метод эквивалентной длины может быть включен в уравнение Дарси-Вейсбаха и выражен в математической форме как:
Обратите внимание, что выражение Σ (L e / D) также умножается на коэффициент трения Moody ƒ, потому что оно обрабатывается так же, как если бы оно было дополнительной длиной той же трубы.
Длина трубы L в уравнении (2) — это длина только прямой трубы. Некоторые авторы рекомендуют включать в L расстояние потока через арматуру, но это неверно. Коэффициент (L e / D) основан на общем падении давления через фитинг и, следовательно, включает любое падение давления из-за длины пути потока. Ошибка небольшая и обычно находится в пределах допустимых значений данных, поэтому попытки измерить все длины пути потока — пустая трата времени, а также техническая ошибка.
Ошибка небольшая и обычно находится в пределах допустимых значений данных, поэтому попытки измерить все длины пути потока — пустая трата времени, а также техническая ошибка.
Применимость данных об эквивалентной длине (L e / D) для режима ламинарного потока будет рассмотрена в разделе 3.4.3 ниже.
3.2 Метод коэффициента сопротивления (K) (иногда называемый методом «коэффициента потерь»)
Этот метод может быть включен в уравнение Дарси-Вейсбаха аналогично тому, как это было сделано выше для метода эквивалентной длины. В этом случае безразмерное число (K) используется для характеристики фитинга без привязки его к свойствам трубы.Это дает начало:
Обратите внимание, что в этом случае сумма коэффициентов сопротивления (ΣK) не умножается на коэффициент трения Муди ƒ. В ранних наборах значений коэффициента сопротивления (K) (например, в Справочнике инженеров-химиков Perry’s Chemical Engineers ‘Handbook, издание 3 , издание , 1950 г. ) давались отдельные значения для каждого типа фитинга, с намерением, чтобы это значение было применимо ко всем размерам этого фитинга. . По мере проведения дополнительных исследований было обнаружено, что в целом коэффициент сопротивления (K) уменьшался с увеличением размера фитинга, и когда Гидравлический институт опубликовал «Руководство по трению труб» в 1954 году, коэффициенты были представлены в виде графиков, охватывающих широкий диапазон диапазон размеров.
) давались отдельные значения для каждого типа фитинга, с намерением, чтобы это значение было применимо ко всем размерам этого фитинга. . По мере проведения дополнительных исследований было обнаружено, что в целом коэффициент сопротивления (K) уменьшался с увеличением размера фитинга, и когда Гидравлический институт опубликовал «Руководство по трению труб» в 1954 году, коэффициенты были представлены в виде графиков, охватывающих широкий диапазон диапазон размеров.
До этого момента полученные значения K использовались только в полностью турбулентном режиме потока, а в справочнике Perry’s Handbook 3 -е издание особо упоминается неприменимость данных к ламинарному (или вязкому) потоку. .
Производитель клапанов, Crane Company, выпускал техническую информацию для расчета расхода с 1935 года и выпустил свой Технический документ № 410 «Поток жидкости через клапаны, фитинги и трубы» в 1942 году. С тех пор этот документ регулярно обновляется и постоянно обновляется. вероятно, наиболее широко используемый источник данных по проектированию трубопроводов в англоязычном мире.В выпуске Crane TP 410 1976 года произошел переломный момент: вместо метода эквивалентной длины (L e / D) появилась собственная версия метода коэффициента сопротивления (K). В литературе это широко называется методом «коэффициента трения крана 2» или просто методом «кран К». Крейн предоставил данные для широкого диапазона фитингов и предоставил метод регулировки значения K для размера фитинга. К сожалению, это долгожданное продвижение привело к значительной ошибке и путанице.Подробности метода Крейна, а также ошибка и источник путаницы обсуждаются отдельно в разделе 4 ниже.
вероятно, наиболее широко используемый источник данных по проектированию трубопроводов в англоязычном мире.В выпуске Crane TP 410 1976 года произошел переломный момент: вместо метода эквивалентной длины (L e / D) появилась собственная версия метода коэффициента сопротивления (K). В литературе это широко называется методом «коэффициента трения крана 2» или просто методом «кран К». Крейн предоставил данные для широкого диапазона фитингов и предоставил метод регулировки значения K для размера фитинга. К сожалению, это долгожданное продвижение привело к значительной ошибке и путанице.Подробности метода Крейна, а также ошибка и источник путаницы обсуждаются отдельно в разделе 4 ниже.
К тому времени, когда в 1963 г. было опубликовано 4 -е издание Справочника Перри, некоторые скудные данные были доступны для коэффициентов сопротивления в режиме ламинарного потока, и они показали, что значение K быстро увеличивалось по мере того, как число Рейнольдса уменьшалось ниже 2000. Первый всесторонний обзор и кодификация коэффициентов сопротивления ламинарного потока, о которых мне известно, был сделан Уильямом Хупером (1981).В этой классической статье Хупер описал свой метод двух К, который учитывал влияние как подходящего размера, так и числа Рейнольдса, используя следующее соотношение:
Первый всесторонний обзор и кодификация коэффициентов сопротивления ламинарного потока, о которых мне известно, был сделан Уильямом Хупером (1981).В этой классической статье Хупер описал свой метод двух К, который учитывал влияние как подходящего размера, так и числа Рейнольдса, используя следующее соотношение:
В этом уравнении K ∞ — это «классический» K для большого фитинга в полностью турбулентном режиме потока, а K 1 — коэффициент сопротивления при числе Рейнольдса 1. Обратите внимание, что, хотя K и Re безразмерны, внутренний диаметр фитинга (D) должен быть указан в дюймах.
Достижения Хупера были сделаны Роном Дарби в 1999 году, когда он представил свой метод трех К. Этот метод используется в калькуляторе размеров труб AioFlo. Уравнение три-K немного сложнее, чем два-K Хупера, но может немного лучше соответствовать имеющимся данным. Это уравнение:
В уравнении (5) посадочный диаметр (D) снова размерный и должен быть в дюймах. Возможно, из-за значительного увеличения вычислительной сложности по сравнению с эквивалентной длиной (L e / D) и методами Crane K, методы two-K и three-K были медленными для достижения большого проникновения в мир проектирования трубопроводов, за исключением их использование в некоторых высокопроизводительных программах, где сложность скрыта от пользователя.Кроме того, оба этих метода страдали от типографских ошибок в своих исходных публикациях, и требуются некоторые усилия, чтобы получить надежные данные, чтобы их можно было использовать, что усугубляет сомнения разработчиков труб в их применении.
Возможно, из-за значительного увеличения вычислительной сложности по сравнению с эквивалентной длиной (L e / D) и методами Crane K, методы two-K и three-K были медленными для достижения большого проникновения в мир проектирования трубопроводов, за исключением их использование в некоторых высокопроизводительных программах, где сложность скрыта от пользователя.Кроме того, оба этих метода страдали от типографских ошибок в своих исходных публикациях, и требуются некоторые усилия, чтобы получить надежные данные, чтобы их можно было использовать, что усугубляет сомнения разработчиков труб в их применении.
Это медленное освоение новых методов отражено в том факте, что работа Хупера 1981 года не вошла в 7 -е издание Справочника Перри 1997 года (в котором все еще перечислены «классические» значения K без поправки на размер или режим потока). Однако это только вопрос времени, когда какая-либо форма multi-K станет частью стандартной методологии определения размеров труб.
Эффективность методов two-K и three-K можно сравнить в диапазоне размеров труб, если учесть, что вода течет через колено стандартного радиуса 90 градусов со скоростью, обеспечивающей падение давления в прямой трубе того же диаметра, равное 3 psi на 100 футов. Для этого упражнения коэффициенты для двух формул были взяты как
Hooper two-K: K 1 = 800, K ∞ = 0,25
Darby three-K: K m = 800, K i = 0,091, K d = 4.0
| Размер трубы дюймов | 2-K Значение К | 3-K Значение К | Diff% (2K-3K) |
|---|---|---|---|
| 1/4 | 1,096 | 0,743 | 38,4 |
| 1/2 | 0,715 | 0,574 | 21,9 |
| 3/4 | 0. | 0,516 | 13,8 |
| 1 | 0,501 | 0,463 | 8,0 |
| 2 | 0,379 | 0,392 | -3,3 |
| 3 | 0,336 | 0,355 | -5,7 |
| 4 | 0,315 | 0.333 | -5,7 |
| 6 | 0,293 | 0,304 | -3,9 |
| 8 | 0,282 | 0,287 | -1,7 |
| 10 | 0,276 | 0,274 | 0,6 |
| 12 | 0,271 | 0,264 | 2. 6 6 |
| 14 | 0,269 | 0,260 | 3,7 |
| 16 | 0,267 | 0,253 | 5,4 |
| 18 | 0,265 | 0,247 | 7,0 |
| 20 | 0,264 | 0,242 | 8,4 |
| 24 | 0.261 | 0,234 | 11,0 |
| 30 | 0,259 | 0,224 | 14,5 |
| 36 | 0,257 | 0,217 | 17,0 |
Таблица сравнения значений K для методов Hooper 2-K и Darby 3-K
(значения приведены для изгиба на 90 градусов стандартного радиуса в турбулентном потоке)
Эта таблица показывает, что для трубопроводов размером от 1 «до 24», которые обычно используются на технологических установках, различия между этими двумя методами невелики. То немногое, что было опубликовано экспериментальных данных, показывает большие вариации, чем различия между этими двумя методами, и предполагает, что оба эти метода являются немного консервативными.
То немногое, что было опубликовано экспериментальных данных, показывает большие вариации, чем различия между этими двумя методами, и предполагает, что оба эти метода являются немного консервативными.
3.3 Коэффициент расхода клапана (C v )
Как следует из названия, этот метод в основном используется в расчетах для клапанов, но, как будет видно далее в этой статье, легко преобразовать между значениями C v и коэффициентом сопротивления (K), поэтому можно определить C v для любого фитинга.
По определению, клапан имеет C v , равный 1, когда давление в 1 фунт / кв. Дюйм вызывает поток 1 галлон США в минуту воды при 60F (т. Е. SG = 1) через клапан. Поскольку перепад давления через клапан пропорционален квадрату расхода, соотношение между C v , расходом и падением давления может быть выражено как:
Это формула размеров, и размеры должны быть в следующих единицах.
Q Объемный расход в галлонах США в минуту
ΔP Падение давления в фунтах на кв. Дюйм
Дюйм
SG Удельный вес жидкости по отношению к воде при 60F
В Великобритании аналогичное выражение используется для определения C v , которое выражается в британских галлонах в минуту, но с использованием тех же единиц измерения падения давления и удельного веса, что и в США.Следует проявлять особую осторожность при использовании значений C v из каталогов производителей клапанов, чтобы определить, какая основа использовалась в определении.
В континентальной Европе клапаны традиционно оценивались с коэффициентом клапана, обозначенным как K v . Это также формула размеров, и единицы измерения определены ниже:
Q ‘объемный расход в кубических метрах в час
ΔP’ падение давления в кгс / см
Удельный вес жидкости относительно воды при 15 ° C
Однако обновленное определение также используется в Европе, которая, наконец, привнесла коэффициент клапана в современную эпоху с помощью единиц СИ. В настоящее время это определение широко не используется, но по мере того, как все больше и больше договорных документов поощряют использование единиц СИ, можно ожидать, что их популярность будет расти. Этот коэффициент называется «Коэффициент площади» и записывается как A v . Его определение:
В настоящее время это определение широко не используется, но по мере того, как все больше и больше договорных документов поощряют использование единиц СИ, можно ожидать, что их популярность будет расти. Этот коэффициент называется «Коэффициент площади» и записывается как A v . Его определение:
Q «объемный расход в кубических метрах в секунду
ΔP» перепад давления в паскалях (≡ Н / м)
ρ плотность жидкости в кг / м
3.4 Сравнение методов эквивалентной длины (L e / D) и коэффициента сопротивления (K)
Как упоминалось ранее, оба этих метода используют множитель с членом скоростного напора для прогнозирования падения давления через фитинг.Следовательно, между ними нет реальной разницы, и при условии использования точных характеристических данных для подгонки оба метода могут дать одинаково точные результаты.
Сравнивая уравнения (2) и (3), мы видим, что константы для двух методов напрямую связаны соотношением:
Таким образом, в любом конкретном случае, когда известны все детали жидкости и трубопроводов, можно получить точное преобразование между константами для двух методов. Однако, когда инженеры говорят о сравнении этих двух методов, реальные вопросы связаны с тем, как значение K или значение L e / D, полученное при одном наборе обстоятельств, может быть использовано при другом наборе обстоятельств. Эти изменившиеся обстоятельства касаются в основном материала трубы, размера фитинга, режима потока (т.е. числа Рейнольдса) и шероховатости самого фитинга.
Однако, когда инженеры говорят о сравнении этих двух методов, реальные вопросы связаны с тем, как значение K или значение L e / D, полученное при одном наборе обстоятельств, может быть использовано при другом наборе обстоятельств. Эти изменившиеся обстоятельства касаются в основном материала трубы, размера фитинга, режима потока (т.е. числа Рейнольдса) и шероховатости самого фитинга.
3.4.1 Влияние материала трубы
Шероховатость трубопровода, прикрепленного к фитингу, не влияет на падение давления в фитинге.Однако, поскольку метод эквивалентной длины (L e / D) выражает перепад давления через фитинг через перепад давления в присоединенном трубопроводе, шероховатость трубы действительно влияет на длину трубопровода, перепад давления в котором будет эквивалентен примерка. Лучше всего это проиллюстрировать на примере:
Расход 150 галлонов США в минуту через 3-дюймовый шаровой клапан с C v 105 (единицы США) приведет к падению давления на 2,05 фунта на кв. Дюйм (с использованием уравнения (6)).На это падение давления не повлияет шероховатость прикрепленной к нему трубы. Если бы труба была из оцинкованной стали с шероховатостью 0,006 дюйма, перепад давления в трубе составлял 2,72 фунта на кв. Дюйм на 100 футов. Длина оцинкованной трубы, которая давала бы эквивалентное падение давления на клапан, составляла бы 75 футов, что дает L . e / D соотношение 290. Если бы трубопровод был гладким из полиэтилена высокой плотности с шероховатостью 0,0002 дюйма, перепад давления в трубе составлял бы всего 1,89 фунта на кв. дюйм на 100 футов, а длина трубопровода из полиэтилена высокой плотности давала бы эквивалентное падение давления на клапане. будет 108 футов, что дает отношение L e / D равное 420.
Дюйм (с использованием уравнения (6)).На это падение давления не повлияет шероховатость прикрепленной к нему трубы. Если бы труба была из оцинкованной стали с шероховатостью 0,006 дюйма, перепад давления в трубе составлял 2,72 фунта на кв. Дюйм на 100 футов. Длина оцинкованной трубы, которая давала бы эквивалентное падение давления на клапан, составляла бы 75 футов, что дает L . e / D соотношение 290. Если бы трубопровод был гладким из полиэтилена высокой плотности с шероховатостью 0,0002 дюйма, перепад давления в трубе составлял бы всего 1,89 фунта на кв. дюйм на 100 футов, а длина трубопровода из полиэтилена высокой плотности давала бы эквивалентное падение давления на клапане. будет 108 футов, что дает отношение L e / D равное 420.
Чтобы можно было использовать метод эквивалентной длины, указанный в уравнении (2), используемые значения L e / D должны строго соответствовать шероховатости используемого трубопровода. На практике различия часто не важны из-за «незначительного» перепада давления в арматуре. В приведенном здесь примере разница составляет 44%, и если это относится к незначительным потерям, которые составляют (скажем) 15% от общих потерь, эффективная погрешность падения давления в трубопроводе составляет всего 7%, и это вполне может быть в пределах общих потерь. допуск расчета.
В приведенном здесь примере разница составляет 44%, и если это относится к незначительным потерям, которые составляют (скажем) 15% от общих потерь, эффективная погрешность падения давления в трубопроводе составляет всего 7%, и это вполне может быть в пределах общих потерь. допуск расчета.
Тем не менее, лучше знать, как были получены заявленные значения L e / D и к каким трубам они могут применяться. К сожалению, значения L e / D, перечисленные в текстах, обычно не упоминают материал трубопровода, но в большинстве случаев это будут чистые стальные трубы промышленного назначения. Неспособность метода эквивалентной длины автоматически справляться с изменениями шероховатости трубы является недостатком этого метода. Мы подготовили исчерпывающие таблицы значений эквивалентной длины в зависимости от шероховатости трубы в другой нашей статье.
Метод коэффициента сопротивления (K) полностью не зависит от шероховатости трубы, и материал присоединенного трубопровода не имеет значения, когда этот метод используется для расчета незначительных потерь.
3.4.2 Влияние размера
В разделе 3.1 было отмечено, что было обнаружено, что соотношение L e / D остается почти постоянным для диапазона размеров данного типа фитинга. С другой стороны, в разделе 3.2 было отмечено, что в целом значения коэффициента сопротивления (K) уменьшаются с увеличением размера фитинга.Чтобы отношение K / ƒ = L e / D из уравнения (9) применялось, оно должно означать, что K / ƒ остается постоянным или что K и ƒ изменяются с одинаковой скоростью. Это наблюдение легло в основу метода Crane K и обсуждается далее в разделе 4 ниже.
При использовании метода эквивалентной длины отношение (L e / D) умножается на коэффициент трения, и, поскольку коэффициент трения уменьшается с увеличением размера трубы, член (ƒL e / D) соответственно уменьшается.Это делает метод эквивалентной длины в значительной степени самокорректирующимся при изменении размера фитинга и делает его очень подходящим для предварительных или ручных расчетов, когда максимальная точность не является главной целью.
Наилучшим доступным методом, доступным в настоящее время для адаптации к изменяющимся размерам труб, по-видимому, является метод Дарби 3-К. Этот метод прогнозирует коэффициенты сопротивления немного выше, чем некоторые из более старых данных, которые учитывали размер фитинга (например, «Руководство по трению труб» Гидравлического института), но поскольку он дается в алгебраической форме, его намного проще использовать в современных таблицах. и компьютерных программ, чем графические данные, представленные в более старых документах.
В качестве иллюстрации рассмотрим изгибы с большим радиусом 2 и 20 дюймов в чистом промышленном стальном трубопроводе. При полностью турбулентном потоке коэффициент сопротивления (K), рассчитанный методом Дарби, будет равен 0,274 для 2-дюймового изгиба и 0,173 для 20-дюймового колена. Это на 37% меньше. Если эквивалентная длина рассчитывается на основе этих значений K и коэффициента трения Moody для чистой трубы из технической стали, то 2-дюймовый изгиб имеет значение (L e / D), равное 13,8, а 20-дюймовый изгиб — 14,0 — a изменение чуть более 1% и настоятельно рекомендуется использовать метод эквивалентной длины.
3.4.3 Влияние режима потока (число Рейнольдса)
Ранние «классические» значения K были измерены в условиях полностью турбулентного потока. Это режим потока, наиболее часто используемый в промышленных приложениях, и это было понятным местом для начала сбора данных. Но было замечено, что при более низких числах Рейнольдса в переходной зоне между Re = 4000 и полностью развитым турбулентным потоком значения K действительно несколько увеличивались. Когда исследования были расширены до ламинарного режима, были обнаружены очень большие увеличения значения K.
Продолжая пример изгибов с большим радиусом, при числе Рейнольдса 100 метод Darby 3-K предсказывает, что и 2 «, и 20» L.R. изгибы будут иметь значение K 8,2. Это огромное увеличение по сравнению с турбулентным потоком. Однако следует помнить, что в режиме ламинарного потока скорости имеют тенденцию быть очень низкими, что делает скоростной напор (v 2 / 2g) низким, и поскольку падение давления рассчитывается как произведение значения K и скоростного напора, Эффект от увеличения K частично компенсируется, и падение давления может быть небольшим в абсолютном выражении.
Опять же, эквивалентные длины могут быть рассчитаны на основе этих значений K и коэффициентов трения Moody, чтобы получить соотношение (L e / D), которое составляет 12,8 для обоих изгибов. Это небольшое изменение в соотношении (L e / D) по сравнению с теми, которые указаны в разделе 3.4.2, несмотря на такое большое изменение числа Рейнольдса, дополнительно усиливает метод эквивалентной длины как очень полезный метод для предварительных и нецелевых критические расчеты.
Есть еще одно соображение относительно режима потока, которое вытекает из инженерных условностей, а не из фундаментальных соображений.Строго говоря, скоростной напор (член кинетической энергии в уравнении Бернулли) должен быть выражен как (αv 2 / 2g). Поправочный коэффициент α необходим, поскольку условно скорость принимается за среднюю скорость (т.е. v = расход / площадь поперечного сечения). На самом деле (средняя скорость) 2 не равна (среднее v 2 ), и поправочный коэффициент используется, чтобы избежать необходимости интегрировать для получения истинного среднего. В турбулентном потоке α очень близко к 1, а в ламинарном потоке имеет значение 2.
В турбулентном потоке α очень близко к 1, а в ламинарном потоке имеет значение 2.
В разделе 2 выше указано, что для расчета падения давления в прямой трубе скоростной напор умножается на коэффициент (ƒL / D). В формуле Дарси-Вейсбаха (уравнение (1)) нет α, так что же нам делать для ламинарного потока? Ответ заключается в том, что по инженерной традиции влияние α поглощается коэффициентом трения. Мы могли бы включить α и использовать коэффициент трения, который составляет только половину от обычного значения, но для простоты арифметики α включается в коэффициент трения ƒ, а скоростной напор принимается равным (v 2 / 2g).
Аналогично поступают с коэффициентами сопротивления (значения K) для трубопроводной арматуры. Мы определяем значения K, чтобы включить значение α, чтобы упростить арифметику.
Есть одно исключение, когда речь идет о мелких убытках. То, что часто называют «потерями на выходе», но точнее — потерями при ускорении, — это кинетическая энергия в потоке, исходящем из выпускного отверстия трубы. Эта энергия теряется и равна одному скоростному напору. Невозможно избежать того, что здесь вы должны использовать правильное значение α, чтобы получить правильные «потери на выходе».Единственной альтернативой было бы определить его так, чтобы значение К было равно 2 в ламинарном потоке, но тогда может показаться, что в ламинарном потоке вы теряете 2 скоростных напора.
Эта энергия теряется и равна одному скоростному напору. Невозможно избежать того, что здесь вы должны использовать правильное значение α, чтобы получить правильные «потери на выходе».Единственной альтернативой было бы определить его так, чтобы значение К было равно 2 в ламинарном потоке, но тогда может показаться, что в ламинарном потоке вы теряете 2 скоростных напора.
На практике это обычно не важно. В ламинарном потоке скорость настолько мала, что один скоростной напор незначителен — и даже если удвоить значение α, равное 2, он все равно будет незначительным. Значения K фитингов в ламинарном потоке могут доходить до сотен или даже тысяч, и одно жалкое 2,0 никого не беспокоит.
3.4.4 Влияние шероховатости посадки
Основными причинами потерь давления в трубопроводной арматуре являются изменение направления и площади поперечного сечения. Оба эти изменения приводят к ускорению жидкости, что потребляет энергию. Конечно, будет некоторое влияние трения между внутренней поверхностью фитинга и жидкостью на падение давления в фитинге, но это необходимо рассматривать в контексте. Придерживаясь примера L.R. изгиба, можно рассчитать, что путь потока через изгиб составляет примерно 2.В 5 раз больше внутреннего диаметра трубы.
Придерживаясь примера L.R. изгиба, можно рассчитать, что путь потока через изгиб составляет примерно 2.В 5 раз больше внутреннего диаметра трубы.
Эквивалентная длина изгиба с большим радиусом обычно принимается (возможно, немного консервативно) равной 16. Если общее падение давления эквивалентно длине трубы в 16 диаметров, и падение давления из-за фактической длины пути потока (которая равна зависит от шероховатости) эквивалентно только 2,5 диаметрам, то можно увидеть, что небольшое изменение трения стенки внутри изгиба будет иметь очень небольшое влияние на общий перепад давления. В фитингах с более высоким сопротивлением, таких как шаровой клапан или сетчатый фильтр, эффект трения еще меньше.
Экспериментальные работы по обтеканию изгибов показали, что шероховатость действительно оказывает заметное влияние на падение давления. Но экспериментальная работа также показывает, что есть измеримые различия в падении давления из-за предположительно одинаковых фитингов разных производителей. Поскольку различия невелики, все общепринятые методы игнорировали шероховатость фитинга и выбирали несколько консервативные значения для (L e / D) и (K).
Поскольку различия невелики, все общепринятые методы игнорировали шероховатость фитинга и выбирали несколько консервативные значения для (L e / D) и (K).
3.5 Преобразование между коэффициентом сопротивления (K) и коэффициентом расхода клапана (C v )
Чтобы иметь возможность преобразовывать значения K и Cv, сначала необходимо переставить уравнения (3) и (6), чтобы они были в аналогичных единицах. Уравнение (3) имеет форму напора жидкости, тогда как уравнение (6) выражено давлением. Соотношение ΔP = ρgh можно использовать для приведения двух уравнений к эквивалентной форме. Аналогично, член скорости в уравнении (3) может быть заменен объемным расходом / площадью, и площадь, конечно, может быть выражена через диаметр трубы.После того, как все эти преобразования и несколько преобразований единиц измерения будут выполнены, соотношение станет:
, где D в дюймах, а C v основано на галлонах США.
4. Метод «2 коэффициента трения» крана для определения коэффициента сопротивления (K)
Нет сомнений в том, что руководство Crane TP 410 «Поток жидкости через клапаны, фитинги и трубы» сыграло важную роль в улучшении качества гидравлических конструкций для трубопроводов за последние 7 десятилетий. Указывая на некоторые слабые стороны метода Crane, этот раздел не нацелен на то, чтобы отвлечь внимание от огромного вклада, внесенного Crane, а, скорее, на то, чтобы выделить те области, в которых за это время достигнут прогресс и в которых инженеры занимаются прокладкой трубопроводов. При расчетах расхода, размера трубы и падения давления в трубе можно использовать более точные методы, доступные в настоящее время.
До 1976 года компания Crane TP 410 использовала метод эквивалентной длины для расчета потерь давления через арматуру.Переход к использованию коэффициентов сопротивления (K) был сделан потому, что они считали, что метод эквивалентной длины приводит к завышенным перепадам давления в режиме ламинарного потока (что частично верно).
Крейн обнаружил, что в условиях полностью турбулентного потока коэффициент сопротивления (K) для многих фитингов менялся в зависимости от диаметра трубы с той же скоростью, с которой коэффициент трения для чистой коммерческой стальной трубы менялся с диаметром. Это показано на Рисунке 2-14 Crane TP 410 (1991).В полностью турбулентном потоке коэффициент трения ƒ T является функцией только ε / D (т. Е. Шероховатости / диаметра), а поскольку ε фиксируется исходя из предположения о чистой промышленной стальной трубе, ƒ T становится функцией только размера трубы . Крейн никогда не заявлял, что более низкие значения ƒ T в больших трубах были причиной снижения коэффициента сопротивления K, но люди часто забывают, что корреляция не подразумевает причинно-следственную связь.
Это показано на Рисунке 2-14 Crane TP 410 (1991).В полностью турбулентном потоке коэффициент трения ƒ T является функцией только ε / D (т. Е. Шероховатости / диаметра), а поскольку ε фиксируется исходя из предположения о чистой промышленной стальной трубе, ƒ T становится функцией только размера трубы . Крейн никогда не заявлял, что более низкие значения ƒ T в больших трубах были причиной снижения коэффициента сопротивления K, но люди часто забывают, что корреляция не подразумевает причинно-следственную связь.
Трудно понять почему, но Крейн полагал, что коэффициенты сопротивления (K), которые были определены таким образом, будут постоянными для всех скоростей потока для данного размера фитинга.Это был странный вывод, поскольку данные о ламинарном потоке начали появляться примерно с 1944 года, а к 1963 году они были достаточно хорошо известны и приняты для упоминания в 4 -м выпуске Perry’s Chemical Engineers ‘Handbook.
Crane воспользовался соотношением между эквивалентной длиной (L e / D) и коэффициентом сопротивления (K), как показано в уравнении (9) выше, чтобы определить новые значения K из их ранее определенной и заявленной эквивалентной длины (L e / D) значения. Все значения (L e / D), накопленные Крейном, были измерены в условиях полностью турбулентного потока и выражены в единицах длины чистой коммерческой стальной трубы. Поэтому они использовали ƒ T , коэффициент трения Moody для полностью турбулентного потока в чистой промышленной стальной трубе соответствующего диаметра, чтобы преобразовать значения эквивалентной длины (L e / D) в значения коэффициента сопротивления (K).
Все значения (L e / D), накопленные Крейном, были измерены в условиях полностью турбулентного потока и выражены в единицах длины чистой коммерческой стальной трубы. Поэтому они использовали ƒ T , коэффициент трения Moody для полностью турбулентного потока в чистой промышленной стальной трубе соответствующего диаметра, чтобы преобразовать значения эквивалентной длины (L e / D) в значения коэффициента сопротивления (K).
В руководстве TP 410 очень четко указано, что значения коэффициента сопротивления (K) следует рассматривать как постоянные для всех скоростей потока, и что следует использовать только коэффициент трения для полностью турбулентного потока в чистой коммерческой стальной трубе ƒ T в преобразовании из старых значений эквивалентной длины (L e / D).Это произошло потому, что они считали, что значения эквивалентной длины (L e / D), которые они определили ранее, действительны только для полностью турбулентного потока, но что как только они были преобразованы в значения коэффициента сопротивления (K), они были применимы ко всем потокам. .
.
Хотя связь между эквивалентной длиной (L e / D) и коэффициентом сопротивления (K) была четко указана как ƒ T , многие инженеры посчитали ее равной всего, или коэффициент трения в подсоединенном трубопроводе, и эти инженеры использовали это соотношение для получения значений K для использования в гладких трубах и для более низких чисел Рейнольдса.Хотя оба этих случая противоречат тому, что задумал Крейн, один из них является верным расчетом, а другой — неверным. Это путаница между корреляцией и причинно-следственной связью, упомянутая ранее.
Как было показано выше в разделе 3.4.1, при работе с гладкой трубой коэффициент сопротивления (K) фитинга остается прежним, но эквивалентная длина (L e / D) изменяется. Поэтому неправильно брать значения крана (L e / D) и использовать более низкий коэффициент трения в гладкой трубе для получения более низкого коэффициента сопротивления (K) из уравнения (9).Присоединение фитинга к гладкой трубе не снижает сопротивления фитинга.
С другой стороны, в разделе 3.4.3 было показано, что при более низких числах Рейнольдса как коэффициент трения, так и коэффициент сопротивления фитинга (K) увеличиваются, в то время как эквивалентная длина (L e / D) фитинга остается постоянной. . Поэтому правильным расчетом является принятие значений крана (L e / D) и использование фактического коэффициента трения ƒ при более низком расходе для получения нового (более высокого) значения коэффициента сопротивления (K), хотя это не как Крейн задумал использовать их метод.
По сути, Крейн взял уравнение (2) и модифицировал его, применив фактический коэффициент трения ƒ в трубе к потоку в трубе (что, очевидно, правильно), одновременно применив коэффициент трения для полностью турбулентного потока в чистой трубы стальные товарные, ƒ T , к эквивалентной длине фитингов. Это показано в уравнении (11):
Вот почему метод Крейна иногда называют K-методом «двух коэффициентов трения». Это также привело к тому, что некоторые инженеры заблуждались по поводу того, что коэффициент трения ƒ T каким-то образом напрямую связан с фитингом, а поскольку фитинг имеет коэффициент трения, он также имеет шероховатость.Вы найдете такие утверждения, как «Нельзя смешивать коэффициент трения фитинга с коэффициентом трения трубы» на инженерных форумах в Интернете, свидетельствуя о том, что фитинги каким-то образом имеют коэффициенты трения. Крейн никогда не предполагал, что люди будут связывать факторы трения с фитингами, но намерения Крейна многие неправильно понимали.
Это также привело к тому, что некоторые инженеры заблуждались по поводу того, что коэффициент трения ƒ T каким-то образом напрямую связан с фитингом, а поскольку фитинг имеет коэффициент трения, он также имеет шероховатость.Вы найдете такие утверждения, как «Нельзя смешивать коэффициент трения фитинга с коэффициентом трения трубы» на инженерных форумах в Интернете, свидетельствуя о том, что фитинги каким-то образом имеют коэффициенты трения. Крейн никогда не предполагал, что люди будут связывать факторы трения с фитингами, но намерения Крейна многие неправильно понимали.
Результатом перехода от метода эквивалентной длины (L e / D) к методу коэффициента сопротивления (K) было (не считая вызванной путаницы), что, хотя метод (L e / D) мог быть завышен давление немного падает в режиме ламинарного потока, новый метод постоянного значения K ужасно занижает их.Примеры в разделах 3.4.2 и 3.4.3 показывают, как коэффициент сопротивления (K) для L.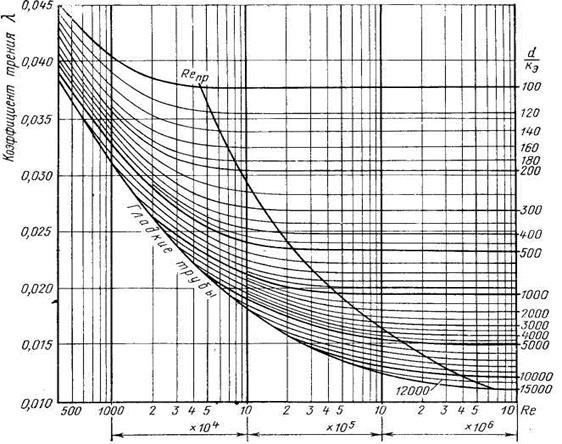 R. изгиб может увеличиваться примерно с 0,2 до 8,2, когда число Рейнольдса падает до 100. К счастью, эта ошибка обычно не является значительной на практике, потому что падение давления через фитинги, как правило, составляет небольшую часть от общего падения давления, и большая ошибка в небольшая часть становится небольшой ошибкой в целом.
R. изгиб может увеличиваться примерно с 0,2 до 8,2, когда число Рейнольдса падает до 100. К счастью, эта ошибка обычно не является значительной на практике, потому что падение давления через фитинги, как правило, составляет небольшую часть от общего падения давления, и большая ошибка в небольшая часть становится небольшой ошибкой в целом.
Когда Crane впервые опубликовал свои рекомендации по проектированию трубопроводов в 1935 году, промышленные трубопроводы изготавливались почти исключительно из углеродистой стали, и методы Crane были нацелены на обеспечение надежных методов проектирования для этой трубы.Кроме того, подавляющее большинство промышленных трубопроводов находится в турбулентном режиме. Крейну, безусловно, удалось разработать комплексный и точный метод расчета турбулентных потоков в стальных трубах. В наше время, когда все чаще используются гладкие пластмассовые и высоколегированные трубы, важно, чтобы инженеры полностью понимали используемые ими методы проектирования и применяли правильный метод для решения поставленной задачи. Правильные методы доступны в методах коэффициента сопротивления 2-К и 3-К, которые обсуждались ранее, и настало время для мира проектирования трубопроводов порвать с прошлым и принять новые методы.
Правильные методы доступны в методах коэффициента сопротивления 2-К и 3-К, которые обсуждались ранее, и настало время для мира проектирования трубопроводов порвать с прошлым и принять новые методы.
5. Точность
Многое из сказанного выше может означать, что определение потерь давления в трубопроводной арматуре является точной наукой. Это не так. Очень мало источников эквивалентной длины (L e / D) или значений коэффициента сопротивления (K) дают пределы точности или неопределенности. Заметным исключением является Книга технических данных Гидравлического института. В лучшем случае неопределенность будет 10%, а в целом 25–30%, вероятно, более реалистичная оценка.
Стандартные фитинги, такие как отводы и тройники, различаются от производителя к производителю, и при расчетах следует принять допуск в 25%. Такие высокоточные элементы, как регулирующие клапаны и измерительные отверстия, конечно, будут иметь гораздо более жесткие допуски, и они обычно указываются в сопроводительной технической документации.
Область, которая требует особого внимания, — это использование общих данных для частных элементов. Многие из таблиц данных включают значения для запатентованных элементов, таких как запорные, шаровые, дроссельные и обратные клапаны, фильтры и тому подобное.Фактические данные о потоке могут сильно отличаться, и можно ожидать отклонения от общих данных от -50% до + 100%.
6. Заключение
В какой-то момент в прошлом метод эквивалентной длины (L e / D) для определения падения давления через трубные фитинги приобрел репутацию неточного. Это было вполне вероятно результатом того, что Крейн отказался от этого метода в пользу метода коэффициента сопротивления (K). В последнее время это отношение в некоторых кругах изменилось, и, надеюсь, проведенный выше анализ поможет убедить большее количество инженеров-проектировщиков в том, что метод эквивалентной длины (L e / D) на самом деле очень полезен и достаточно точен во многих ситуациях. Однако у этого метода есть два серьезных недостатка. Это необходимость определения характеристик падения давления фитинга с точки зрения произвольного внешнего фактора (например, присоединенного трубопровода) и неспособность этого метода справиться с входами, выходами и фитингами с двумя характерными диаметрами (например, изменения диаметра и отверстия). По этим причинам метод коэффициента сопротивления (K) является лучшим способом точных и всесторонних расчетов.
Однако у этого метода есть два серьезных недостатка. Это необходимость определения характеристик падения давления фитинга с точки зрения произвольного внешнего фактора (например, присоединенного трубопровода) и неспособность этого метода справиться с входами, выходами и фитингами с двумя характерными диаметрами (например, изменения диаметра и отверстия). По этим причинам метод коэффициента сопротивления (K) является лучшим способом точных и всесторонних расчетов.
Метод 3-K Дарби позволяет учитывать размер фитинга и режим потока.Количество доступных данных постепенно увеличивается и в настоящее время примерно соответствует объему базы данных Crane TP 410. Некоторое программное обеспечение более высокого уровня уже перешло на использование метода Дарби, и можно ожидать, что со временем он получит более широкое распространение.
Данные в Crane TP 410 остаются очень ценным ресурсом, но их следует использовать с пониманием диапазона их применимости. К счастью, эти данные наиболее точны в зоне полностью турбулентного потока, где работает большая часть трубопроводов. Ошибки, вносимые этим методом, когда расход ниже полностью турбулентного режима, могут быть большими по сравнению с потерями в самих фитингах, но поскольку они часто составляют небольшую часть общих потерь, ошибки часто незначительны. Как всегда, понимание точности используемых методов позволяет инженеру достичь безопасного и экономичного проектирования.
Ошибки, вносимые этим методом, когда расход ниже полностью турбулентного режима, могут быть большими по сравнению с потерями в самих фитингах, но поскольку они часто составляют небольшую часть общих потерь, ошибки часто незначительны. Как всегда, понимание точности используемых методов позволяет инженеру достичь безопасного и экономичного проектирования.
7. Список литературы
Crane Co. Поток жидкостей через клапаны, фитинги и трубы.Техническая бумага 410, 1991
Darby, R. Chem Eng, июль 1999 г., стр. 101
Darby, R. Chem Eng, апрель 2001 г., стр. 127
Хупер, ВБ. Chem Eng, 24 августа 1981 г., стр. 97
Гидравлический институт, Руководство по трению труб, Нью-Йорк, 1954,
.
Гидравлический институт, Технические данные, 2 nd ed, 1991
Перри, Дж. Х. «Справочник инженеров-химиков», 3 rd ed, McGraw-Hill, 1950
Перри, Р. Х. и Чилтон, Швейцария. «Справочник инженеров-химиков», 4 th ed, McGraw-Hill, 1963
Перри, Р.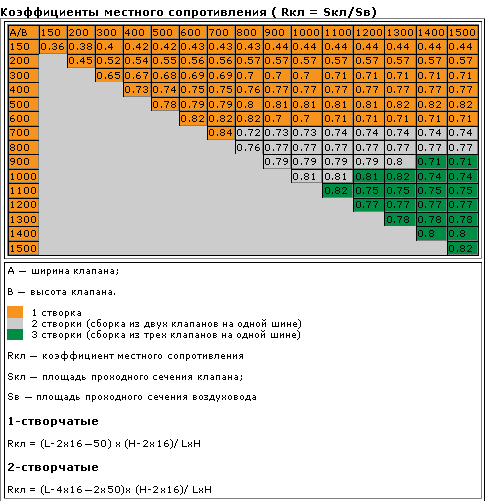 Х. и Грин, Д.В.»Справочник инженеров-химиков», 7 th ed, McGraw-Hill, 1997
Х. и Грин, Д.В.»Справочник инженеров-химиков», 7 th ed, McGraw-Hill, 1997
HTflux — Программное обеспечение для моделирования
На последней вкладке диалогового окна инструмента сопротивления теплопередаче в HTflux вы найдете очень универсальный инструмент для расчета коэффициентов теплопередачи (сопротивления) потоков в трубах для газов и жидкостей.
Чтобы получить эти фактические коэффициенты переноса, необходимы некоторые гидродинамические расчеты. К счастью, HTflux сделает эту работу за вас, помимо тепловых коэффициентов, он также предоставит вам множество других важных показателей, например.грамм. он рассчитает падение давления для указанной трубы.
Инструмент для расчета расхода труб
Инструмент очень эффективен, если вы пытаетесь рассчитать теплопотери (или теплопотери) труб, содержащих текущую среду. Это может быть актуально для многих приложений, например трубы отопления, охлаждающие трубы, вентиляционные трубы, дымоходы, теплообменники, котлы, конденсаторы, испарители, трубы холодной воды, трубы горячей воды, трубы холодильников, трубы двигателя,…
Вам останется только указать желаемые входные параметры.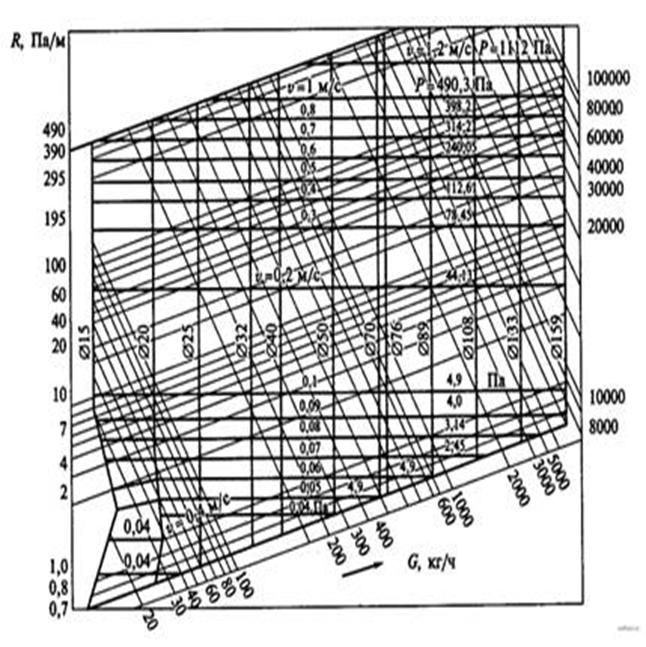 Это:
Это:
- Диаметр трубы: введите внутренний диаметр трубы.
- Длина трубы: введите соответствующую длину вашей трубы.
- Температура жидкости: введите здесь среднюю температуру жидкости.
- Жидкость: здесь вы можете выбрать тип жидкости в вашей трубе.
В настоящее время доступны следующие жидкости (другие могут быть добавлены по запросу):- Вода (при 1 бар)
- Воздух (сухой, при 1 атм)
- Хладагент R134a в жидкой фазе
- Хладагент R134a в паровой фазе
- Водяной пар (пар)
- Аммиак в жидкой фазе
- Аммиак в паровой фазе
- Пропан в жидкой фазе
- Пропан в паровой фазе
- Изобутан R600a
- Моторное масло (чистое, неиспользованное)
- Расход: здесь вы можете указать расход в литрах в минуту
- Скорость потока: здесь можно указать среднюю скорость потока в м / с, скорость потока будет рассчитываться соответственно.
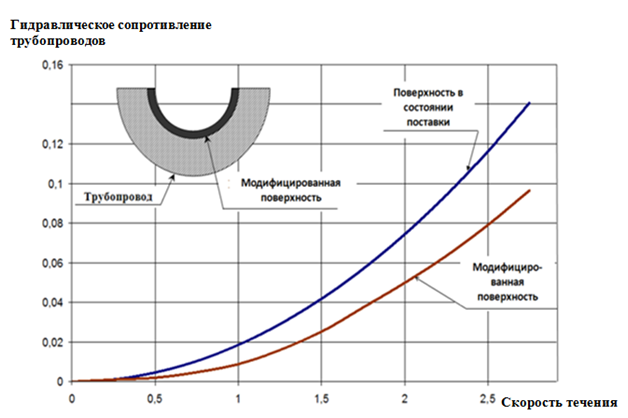
- Модель трения: вы можете выбрать одну из трех различных моделей трения для расчета:
- Colebrook-White: оставьте значение по умолчанию, если вы не уверены.
- Никурадсе: на основе шероховатости песчаника
- Модель гладкой трубы: на основе расчета Прандтля
- Шероховатость трубы : здесь вы можете указать абсолютную шероховатость трубы, например для полиэтиленовых труб обычно указывается шероховатость 0,003 мм.
После задания требуемых параметров HTflux рассчитает значение поверхностного сопротивления теплопередачи труб.При нажатии на кнопку «ОК» значение будет присвоено выбранному граничному условию. Используйте это граничное условие вместе с правильной средней температурой в моделировании для расчета теплопередачи потока в вашей трубе.
Физика потока и теплообмена в трубах — краткий обзор
Поскольку HTflux выполнит расчеты за вас, вам не придется углубляться в гидродинамику, однако основные этапы расчета будут описаны в следующих параграфах.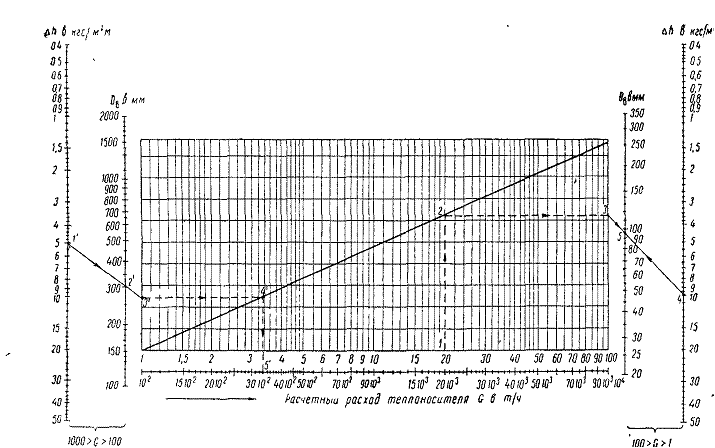 Передача тепла от текущей жидкости к внутренней поверхности трубы / трубки сильно зависит от фактического состояния потока.Поэтому необходимо рассчитать основные характеристические параметры, которые используются для описания состояния потока жидкости.
Передача тепла от текущей жидкости к внутренней поверхности трубы / трубки сильно зависит от фактического состояния потока.Поэтому необходимо рассчитать основные характеристические параметры, которые используются для описания состояния потока жидкости.
После того, как вы выбрали тип жидкости и ее температуру, HTflux определяет соответствующие свойства вашей жидкости: плотность, теплопроводность, теплоемкость, кинетическую вязкость и коэффициент температуропроводности. На основе этого рассчитывается так называемое число Прандтля . Это отношение вязкости (импульсной диффузии) и температуропроводности, поэтому оно важно для этого расчета.
Число Рейнольдса
На следующем этапе будет вычислено число Рейнольдса для потока в трубе:
Число Рейнольдса является важной величиной, которая позволяет прогнозировать состояние потока жидкости. На основе фактического значения числа Рейнольдса расчет будет продолжен либо для ламинарного (Re <2300), либо для турбулентного случая (Re> = 2300), поскольку эти два состояния потока имеют существенно различающееся поведение: 900 · 10
Турбулентный поток в трубе
Когда число Рейнольдса превышает значение 2300, можно предположить турбулентный поток . Эффекты турбулентности приводят к более высокой скорости «перемешивания» в потоке и, следовательно, значительно увеличивают скорость теплопередачи. Число Нуссельта , описывающее такой поток, можно записать как:
Эффекты турбулентности приводят к более высокой скорости «перемешивания» в потоке и, следовательно, значительно увеличивают скорость теплопередачи. Число Нуссельта , описывающее такой поток, можно записать как:
, где Pr — это число Прандтля , Re — это число Рейнольдса , λ — коэффициент трения дарцитона . трубы (см. Ниже), d — внутренний диаметр, а L — длина трубы.
Трубопровод ламинарный
Если число Рейнольдса находится ниже значения 2300, предполагается ламинарный поток.В этом случае предполагается плавный, равномерный поток в трубе. Скорость потока меняется в зависимости от радиуса. Наибольшая скорость достигается в центре трубы, где скорость на поверхности трубы достигает значения 0. Из-за такого характерного распределения теплопередача на внутреннюю поверхность трубы значительно ниже, чем в турбулентном потоке. . Для этого ламинарного корпуса число Нуссельта можно записать как:
Коэффициенты трения для потока в трубе
Как упоминалось выше, вы можете выбирать среди различных моделей трения. За исключением особых случаев, выбор модели не окажет большого влияния на результаты расчета. Если вы не уверены, мы рекомендуем выбрать модель Colebrook-White и указать шероховатость трубы, указанную в конкретном информационном бюллетене по трубе или аналогичных документах.
За исключением особых случаев, выбор модели не окажет большого влияния на результаты расчета. Если вы не уверены, мы рекомендуем выбрать модель Colebrook-White и указать шероховатость трубы, указанную в конкретном информационном бюллетене по трубе или аналогичных документах.
В зависимости от состояния потока и выбранной модели будут использоваться следующие уравнения:
Ламинарный поток — коэффициент трения Дарси
Как описано ранее, в случае ламинарного потока жидкость, касающаяся поверхности трубы, всегда будет «прилипать» к поверхности трубы (v = 0).Следовательно, в таком случае коэффициент трения не будет зависеть от шероховатости трубы. Следовательно, для коэффициента трения Дарси для всех ламинарных потоков будет использоваться следующее уравнение:
Колбрук-Уайт фрикционная модель
Для большинства приложений эта модель обеспечит наилучшие результаты. Может быть предусмотрена определенная шероховатость k трубы, однако модель также дает хорошие результаты для гладких труб.
Модель трения Никурадсе
Основываясь на экспериментах с песчинками, Никурадсе разработал модель трения, которая лучше всего подходит для поверхностей с подобным типом «шероховатости песка».Соответствующее уравнение для этой модели:
Гладкая труба, модель
Для турбулентных течений в идеально гладких трубах можно использовать следующее уравнение (Кармана-Никурдсе / Прандтля):
Коэффициент теплопередачи для потока в трубе
После того, как все соответствующие величины потока были рассчитаны, легко окончательно рассчитать коэффициент теплопередачи потока в трубе — или его обратное поверхностное сопротивление Rs, используемое в HTflux. Число Нуссельта в основном содержит всю необходимую информацию.Это должно быть связано только с внутренним диаметром трубы и теплопроводностью жидкости:
Другие полезные данные о расходе в трубопроводе: падение давления, сопротивление трубопровода и коэффициент потери давления
Наряду с показателями теплопередачи HTflux предоставляет вам также полезные данные о конструкции труб. Используя эти цифры, вы можете легко рассчитать падение давления при заданном расходе (или наоборот).
Используя эти цифры, вы можете легко рассчитать падение давления при заданном расходе (или наоборот).
HTflux использует следующие уравнения для этой задачи:
для ламинарных трубных потоков:
Коэффициент сопротивления / гидравлический градиент (R в кг / м 7 ):
Падение давления (ΔP в Па):
Дзета-значение (ζ):
для турбулентных трубопроводных потоков:
Коэффициент сопротивления / гидравлический градиент (R в кг / м 7 ):
Падение давления (Δp в Па):
Дзета-значение (ζ):
(c) HTflux, Даниэль Рюдиссер
Примечание. Вам разрешается и поощряется использование изображений с этой страницы или установка ссылки на эту страницу при условии, что авторство указано на «www.htflux.com ».
Трубы и калибровка труб | Спиракс Сарко
Размер трубопровода
Важность определения размеров трубопровода
Задача любой системы распределения жидкости — подавать жидкость под нужным давлением к месту использования.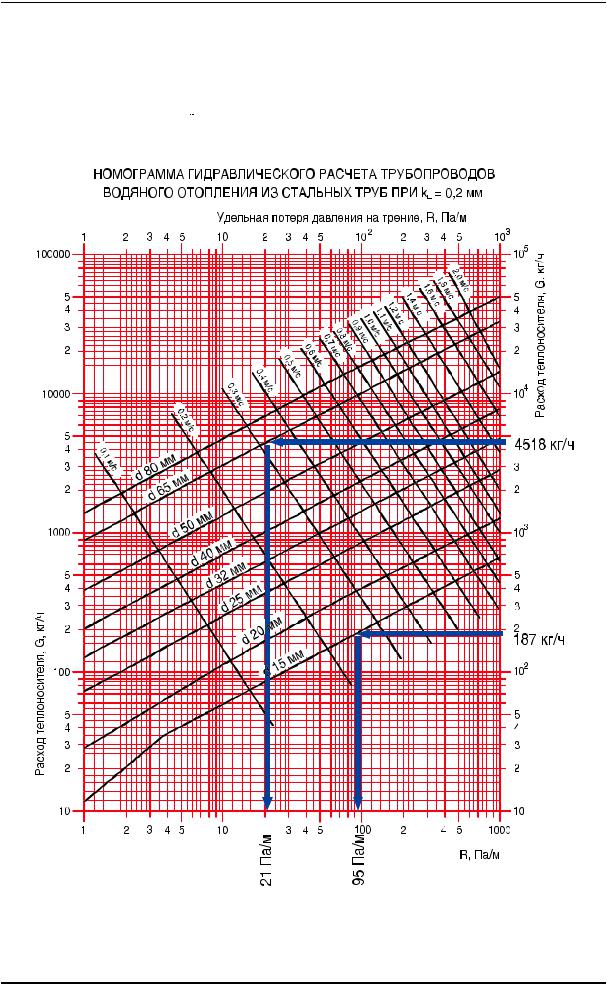 Отсюда следует, что падение давления в системе распределения является важной характеристикой.
Отсюда следует, что падение давления в системе распределения является важной характеристикой.
Размер трубопровода для жидкостей
Теорема Бернулли (Даниэль Бернулли 1700–1782) обсуждается в Блоке 4 — Измерение расхода.Д’Арси (D’Arcy Thompson 1860–1948) добавил, что для возникновения потока жидкости в точке 1 должно быть больше энергии, чем в точке 2 (см. Рис. 10.2.3). Разница в энергии используется для преодоления сопротивления трения между трубой и текущей жидкостью.
Бернулли связывает изменения в общей энергии текущей жидкости с рассеянием энергии, выраженным либо в терминах потери напора hf (м), либо в единицах удельных потерь энергии g hf (Дж / кг). Само по себе это не очень полезно, если не будет возможности предсказать потери давления, которые возникнут в определенных обстоятельствах.
Здесь вводится один из наиболее важных механизмов диссипации энергии в протекающей жидкости, то есть потеря общей механической энергии из-за трения о стенку однородной трубы, по которой проходит устойчивый поток жидкости.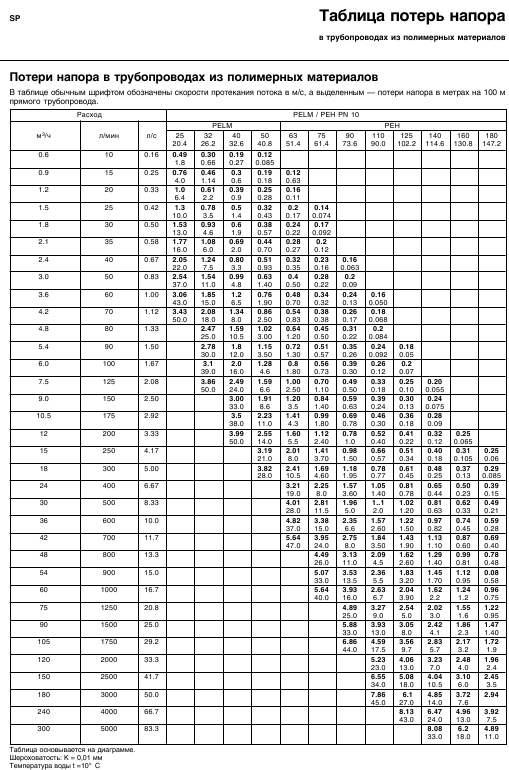
Потери общей энергии жидкости, протекающей по круглой трубе, должны зависеть от:
L = Длина трубы (м)
D = Диаметр трубы (м)
u = Средняя скорость потока жидкости (м / с)
μ = динамическая вязкость жидкости (кг / м · с = Па · с)
курсив-p — основной текст.jpg = Плотность жидкости (кг / м³)
kS = шероховатость стенки трубы * (м)
* Поскольку рассеяние энергии связано с напряжением сдвига на стенке трубы, природа поверхности стенки будет иметь значение, поскольку гладкая поверхность будет взаимодействовать с жидкостью иначе, чем шероховатая поверхность.
Все эти переменные собраны вместе в уравнении Д’Арси-Вейсбаха (часто называемом уравнением Д’Арси) и показаны как уравнение 10.2.1. Это уравнение также вводит безразмерный термин, называемый коэффициентом трения, который связывает абсолютную шероховатость трубы с плотностью, скоростью и вязкостью жидкости и диаметром трубы.
Термин, который связывает плотность, скорость и вязкость жидкости, а также диаметр трубы, называется числом Рейнольдса в честь Осборна Рейнольдса (1842-1912, из колледжа Оуэнс, Манчестер, Соединенное Королевство), который впервые применил этот технический подход к потерям энергии при протекании. жидкости около 1883 г.
жидкости около 1883 г.
Уравнение Д’Арси (Уравнение 10.2.1):
Читатели в некоторых частях мира могут узнать уравнение Д’Арси в несколько иной форме, как показано в уравнении 10.2.2. Уравнение 10.2.2 аналогично уравнению 10.2.1, но не содержит константы 4.
Причина разницы в типе используемого коэффициента трения. Важно использовать правильную версию уравнения Д’Арси с выбранным коэффициентом трения. Сопоставление неправильного уравнения с неправильным коэффициентом трения приведет к ошибке 400%, и поэтому важно использовать правильную комбинацию уравнения и коэффициента трения. Во многих учебниках просто не указывается, какие коэффициенты трения определены, и иногда суждение должно основываться на указанных величинах.
Уравнение 10.2.2, как правило, используется теми, кто традиционно работает в имперских единицах измерения, и все еще имеет тенденцию использоваться практиками в Соединенных Штатах и регионах Тихоокеанского региона, даже когда указаны метрические размеры труб. Уравнение 10.2.1 обычно используется теми, кто традиционно работает в единицах СИ, и чаще используется европейскими специалистами-практиками. Для того же числа Рейнольдса и относительной шероховатости «коэффициент трения в британской системе мер» будет ровно в четыре раза больше, чем «коэффициент трения в системе СИ».
Уравнение 10.2.1 обычно используется теми, кто традиционно работает в единицах СИ, и чаще используется европейскими специалистами-практиками. Для того же числа Рейнольдса и относительной шероховатости «коэффициент трения в британской системе мер» будет ровно в четыре раза больше, чем «коэффициент трения в системе СИ».
Коэффициенты трения могут быть определены либо с помощью диаграммы Moody, либо, для турбулентных потоков, могут быть рассчитаны с помощью уравнения 10.2.3, являющегося развитием формулы Колебрука-Уайта.
Однако уравнение 10.2.3 трудно использовать, потому что коэффициент трения появляется с обеих сторон уравнения, и именно по этой причине ручные расчеты, вероятно, будут выполняться с использованием диаграммы Moody.
На диаграмме Moody в стиле СИ шкала коэффициента трения обычно может находиться в диапазоне от 0.002–0,02, тогда как на диаграмме Moody в имперском стиле этот масштаб может находиться в диапазоне от 0,008 до 0,08.
Как правило, для турбулентного потока с числами Рейнольдса от 4000 до 100000 коэффициенты трения, основанные на системе СИ, будут иметь порядок, предложенный уравнением 10. 2.4, в то время как коэффициенты трения на основе британских мер будут предложенного порядка по уравнению 10.2.5.
2.4, в то время как коэффициенты трения на основе британских мер будут предложенного порядка по уравнению 10.2.5.
Используемый коэффициент трения будет определять, используется ли уравнение Д’Арси: 10.2.1 или 10.2.2.
Для коэффициентов трения, основанных на системе СИ, используйте уравнение 10.2.1; для коэффициентов трения, основанных на британской системе мер, используйте уравнение 10.2.2.
Пример 10.2.1 Водопровод
Определите скорость, коэффициент трения и разницу давлений между двумя точками на расстоянии 1 км в системе горизонтальных трубопроводов постоянного диаметра 150 мм, если расход воды составляет 45 м³ / ч при 15 ° C.
По сути, коэффициент трения зависит от числа Рейнольдса (R e ) текущей жидкости и относительной шероховатости (k S / d) внутренней части трубы; первое рассчитано по уравнению 10.2.6, а последнее — из уравнения 10.2.7.
Число Рейнольдса (R e )
Шероховатость трубы или значение ‘k S ‘ (в некоторых текстах часто цитируется как curly-e — body text.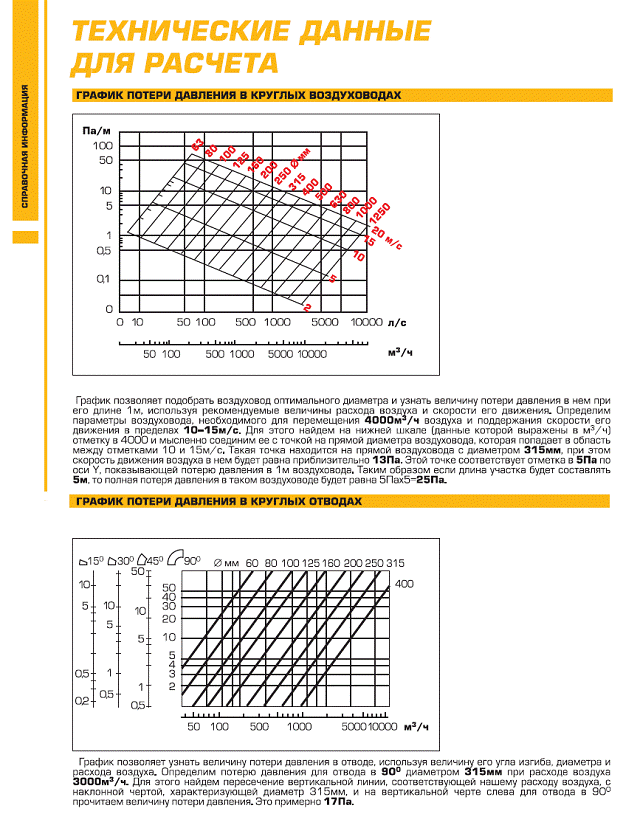 jpg) взято из стандартных таблиц, а для «промышленных стальных труб» обычно принимается равным 0,000 045 метров.
jpg) взято из стандартных таблиц, а для «промышленных стальных труб» обычно принимается равным 0,000 045 метров.
Отсюда определяется относительная шероховатость (как этого требует диаграмма Moody).
Теперь коэффициент трения можно определить по диаграмме Moody, а потерю напора на трение рассчитать по соответствующему уравнению Д’Арси.
Из европейского графика Moody (рисунок 10.2.4),
Где: k S / D = 0,000 3 R e = 93585: Коэффициент трения (f) = 0,005
Из графика Moody для США / Австралии (рис. 10.2.5),
Где: kS / D = 0,000 3 Re = 93585 Коэффициент трения (f) = 0,02
Такая же потеря напора на трение получается при использовании различных коэффициентов трения и соответствующих уравнений Д’Арси.
На практике, будь то водопроводные или паровые трубы, балансируется между размером трубы и потерей давления.
Pipe Flow Software также имеет веб-сайт www.  pipeflow.com (на котором в настоящее время есть дополнительная информация) pipeflow.com (на котором в настоящее время есть дополнительная информация) Программа Pipe Flow Expert: Расчет расхода и падения давления в трубе Попробуйте Pipe Flow Expert прямо сейчас!
| ||||
DNV GL’s PKI Калькулятор метанового числа для трубопроводного газа
Сокращение местных запасов природного газа означает, что для удовлетворения спроса необходимо импортировать больше газа по трубопроводу или по морю в виде СПГ. Поскольку этот газ поступает из различных запасов по всему миру и предназначен для различных рынков, его состав может значительно различаться, и, таким образом, импортируемый природный газ обычно имеет состав, отличный от традиционно распределяемого газа.В то же время стремление к «более зеленой» инфраструктуре природного газа за счет введения возобновляемых газов в газовую сеть привело к устойчивому увеличению закачки газообразного топлива из биомассы в сеть, при этом планируются другие возобновляемые газы (например, H 2 и синтез-газ).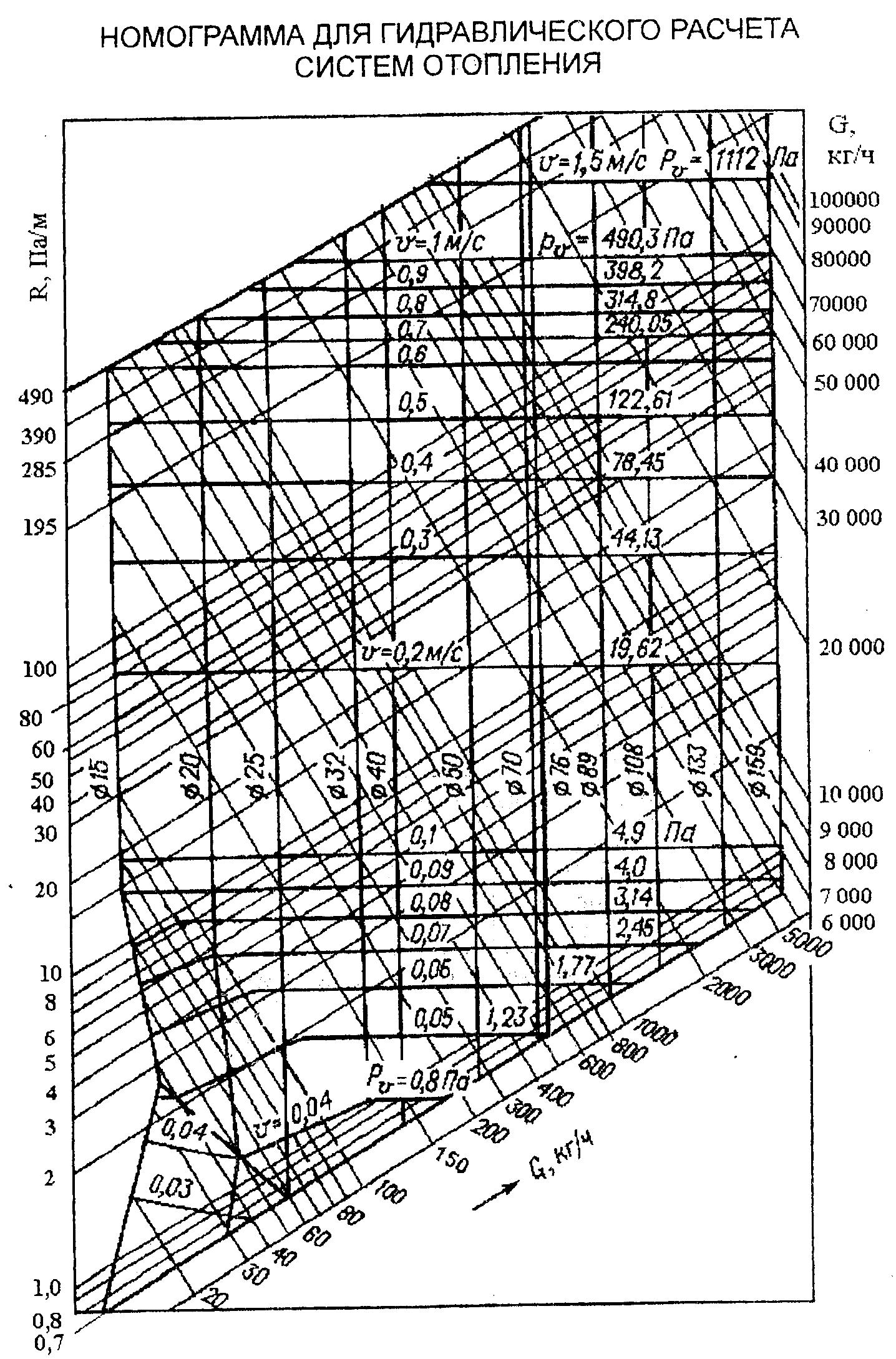 Различные составы могут иметь разные свойства горения, что может привести к неприемлемым изменениям в безопасности или пригодности оборудования для конечного использования. Для оптимальной и безопасной работы газовых двигателей очень важно точно определять детонационную стойкость газов.
Различные составы могут иметь разные свойства горения, что может привести к неприемлемым изменениям в безопасности или пригодности оборудования для конечного использования. Для оптимальной и безопасной работы газовых двигателей очень важно точно определять детонационную стойкость газов.
Теперь доступно: Калькулятор метанового числа PKI для трубопроводного газа
Чтобы определить пригодность для использования в трубопроводном газе, DNV GL разработала общий метод следующего поколения для количественной оценки ударопрочности трубопроводных газов на основе характеристик горения топливо.
Подобно существующему калькулятору метанового числа DNV GL PKI для СПГ, калькулятор трубопроводного газа вычисляет метановое число PKI для количественной оценки так называемой детонационной стойкости топлива по шкале от 0 до 100, аналогичной октановому числу бензина.Калькулятор позволяет рассчитывать составы, обычно присутствующие в трубопроводном газе и трубопроводных газах, смешанных с возобновляемыми газами, такими как H 2 , CO, CO 2 и существенные доли N 2 . Прогнозы стойкости к детонации для широкого диапазона топливных композиций были проверены для двигателя с обедненной смесью в конфигурации для комбинированного производства тепла и электроэнергии (ТЭЦ) и демонстрируют превосходные характеристики по сравнению с традиционными методами. Поскольку наш метод основан на физических и химических процессах, которые определяют детонацию, адаптировать его к новым платформам двигателей и топливным композициям несложно.Например, вместе с группой ключевых клиентов DNV GL в настоящее время применяет этот метод к различным моторным платформам, которые используют СПГ в качестве топлива (грузовые, судовые и ТЭЦ).
Прогнозы стойкости к детонации для широкого диапазона топливных композиций были проверены для двигателя с обедненной смесью в конфигурации для комбинированного производства тепла и электроэнергии (ТЭЦ) и демонстрируют превосходные характеристики по сравнению с традиционными методами. Поскольку наш метод основан на физических и химических процессах, которые определяют детонацию, адаптировать его к новым платформам двигателей и топливным композициям несложно.Например, вместе с группой ключевых клиентов DNV GL в настоящее время применяет этот метод к различным моторным платформам, которые используют СПГ в качестве топлива (грузовые, судовые и ТЭЦ).
Пользователь просто вводит состав газовой смеси трубопровода в качестве входных данных, и инструмент вычисляет метановое число PKI, которое можно сравнить с требованиями двигателя.
К сожалению, онлайн-калькулятор сейчас недоступен.
Мы работаем над тем, чтобы исправить это как можно скорее.
Свяжитесь с Мартин ван Эссен (M.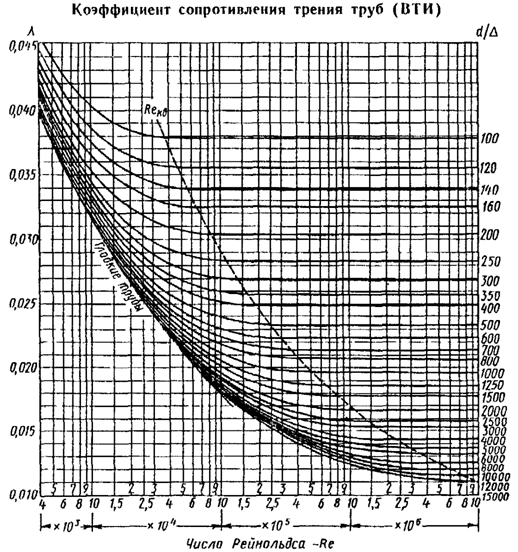

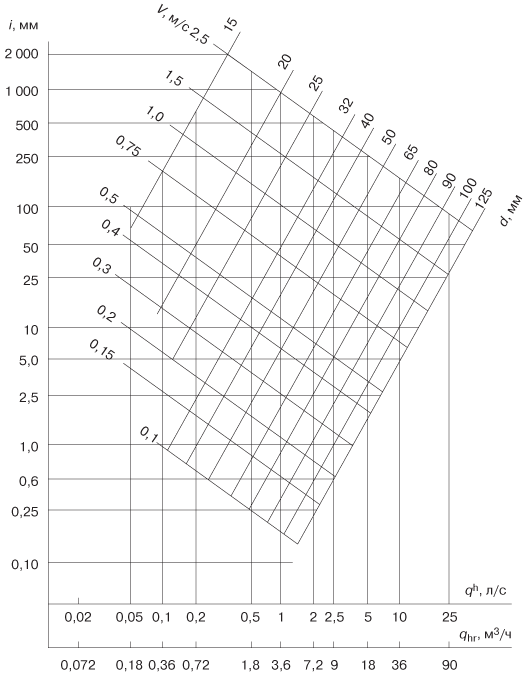 = 250-300 мм
= 250-300 мм 00 фунтов стерлингов составляет примерно 1,42 доллара США или примерно 1,17 евро за евро.
00 фунтов стерлингов составляет примерно 1,42 доллара США или примерно 1,17 евро за евро.
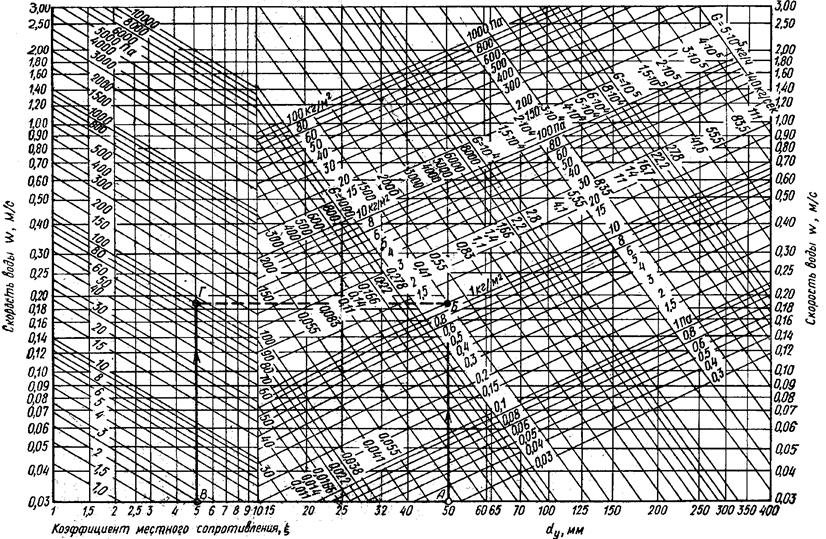 Неограниченное использование.
Неограниченное использование. Свяжитесь с нами по электронной почте
нам с вашими требованиями, чтобы получить цитату.
Свяжитесь с нами по электронной почте
нам с вашими требованиями, чтобы получить цитату.