Определите глубину колодца если упавший в него камень коснулся дна: Определить глубину колодца,если камень упавший в него,коснулся дна колодца через 2 секунды.

Возле колодца нельзя ни бурить ни копать, можно нарушить глиняный замок. Вода может вообще уйти, если под водоупором вскроется песок.

У меня в практике был такой случай —

Позвонил мне мой клиент, мы ему колодец строили 18 колец. И говорит:

— Вы не могли бы приехать?

— Что случилось?

— Вода из колодца ушла! Сухой колодец!

Выяснилось, что сосед пытался пробурить скважину. Буровики сделали несколько попыток дойти до воды, может камни, или вода глубоко, но у них ничего не получилось, так и уехали. Две скважины пробурили в 8 м от колодца. Видимо туда вода и ушла.

В Санкт-Петербурге все, кто занимается колодцами, навязывают своим клиентам разведочное бурение — это можно судить по Питерским сайтам. Во внимание не берутся даже соседние колодцы — это говорит о непрофессионализме копателей или о мошенничестве.

Заказчика убеждают в том, что у соседа вода может быть одного качества, а у Вас совсем другого. Необходимо знать — в какую сторону движутся воды, и заказчик точно будет знать, сколько колец ему нужно для колодца.

Убедительно звучит! Каждый клиент, я думаю, желал бы знать эту информацию о будущем колодце. Но есть в этом деле некое лукавство со стороны «разведчиков»:

1. Качество воды невозможно узнать таким способом, так как пока вода в скважине не отстоится, анализы брать бессмысленно. А для этого необходимо, чтобы вода в скважине стояла в состоянии покоя 3-4 недели. Результаты могут измениться, если колодезники не докопают или пройдут разведочный порог.

2. Глубина колодца напрямую зависит от колодезников и от их мастерства в этом деле. Большинство специалистов по колодцам в Питере вообще не умеют строить колодцы. Нередко колодцы сдают без воды.

3. Для чего «разведчикам» знать, в какую сторону движутся воды и каким образом они это определяют, заглядывая в скважину, ума не приложу!

Если местность холмистая, то движение воды происходит по закону физики — сверху вниз. На равнине, если и есть движение грунтовых вод, его невозможно определить.

Деятельность «разведчика»в большинстве случаев — бессмысленная затея. Ни один «разведчик» Вам не скажет точно, сколько колец понадобится для вашего колодца.

Практически все, кто заказывает колодцы, вообще ничего не понимают в строительстве колодцев. Этим и пользуются недобросовестные предприниматели.

Разведкой профессионалы по колодцам не пользуются. Если мастера занимаются строительством не один год, то территорию они знают: где, какие и какой глубины колодцы, какая вода в них.

Не позволяйте себя обманывать!

1. Разновидность колодцев
2. Как найти хороших мастеров?
3. Ошибки заказчика при строительстве питьевого колодца
4. Кольца для питьевых колодцев — какие они?
5. Формирование колодца
6. Как выбрать место для колодца?
7. Поиск воды с помощью рамки и лозы
8. Камни и деревянный щит на дне колодца
9. Как определить глубину колодца?
10. Глиняный замок
11. Нужно ли делать вокруг колодца бетонную отмостку?
12. Трубопровод от колодца в дом
13. Углубление колодца
14. Какое расстояние должно быть от колодца до септика?
15. Когда нужно чистить колодец?
16. Почему вода в колодце стала мутной?
17. Колодец на две семьи. 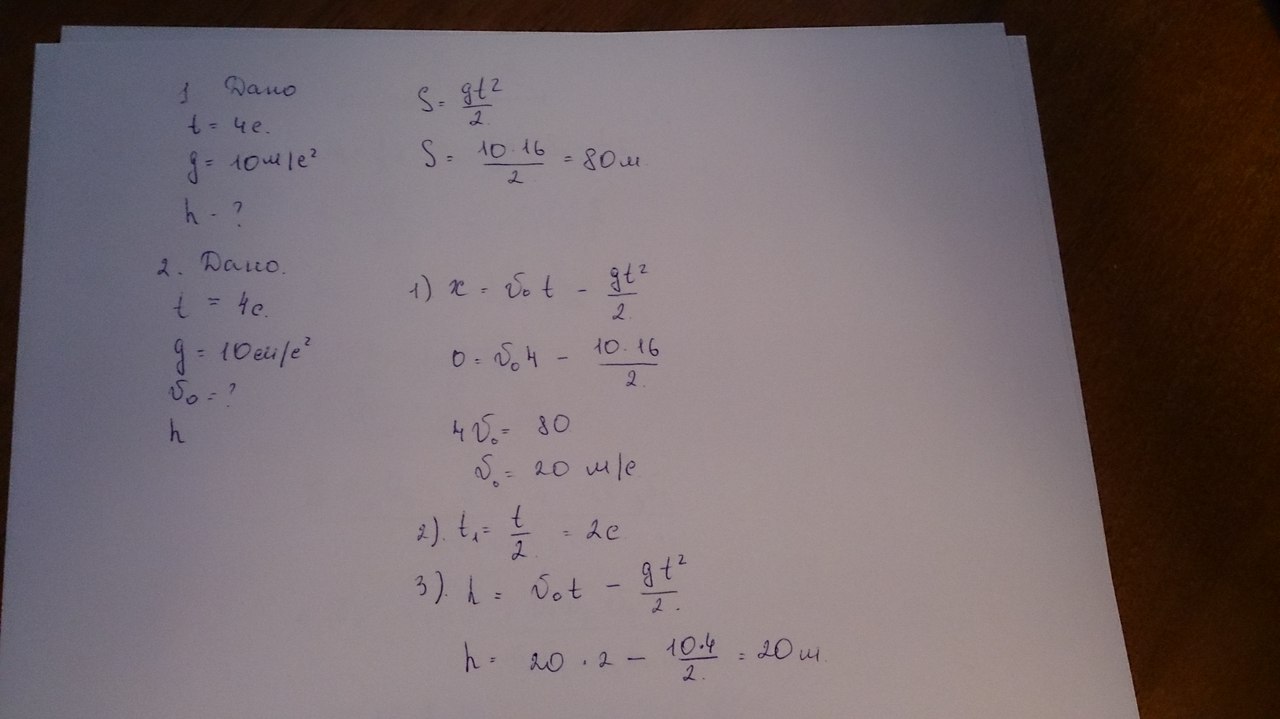Можно ли его сделать глубже?
18. Какие гарантии, что колодец будет хороший?
19. Мы находимся далеко от Москвы за 300 км?
20. А у Вас бывают неудачные колодцы?
21. У меня участок ухожен, переживаю за последствия вашей деятельности
22. Если колодец не получился?
23. Мне нужно копать колодец до песка!
24. Сколько человек работает при строительстве колодца, нужно ли жильё?
25. Скважина или колодец?
26. Колодцы зимой
27. Вредные советы
28. Родниковые питьевые колодцы
29. Отношение бригад к колодцам
30. Чистая ли вода в колодце?
31. Плохая вода в колодце
32. Наплевательское отношение к колодцу
33. Вода в колодцах чище чем в родниках
34. Почвенные и грунтовые воды. В чём различие?

Насколько глубок колодец?

Представьте, что вы стоите рядом с колодцем неизвестной глубины. Вы хотите оценить расстояние от поверхности до воды. Вы берете ближайший камень и бросаете его в колодец, осторожно запуская секундомер в тот самый момент, когда отпускаете камень.

Через 5,8 секунды вы услышите приятный всплеск. Насколько глубока скважина?

Через 5,8 с вы услышите приятный всплеск. Насколько глубока скважина?

(Пожалуйста, на самом деле не бросайте вещи в колодцы, это похоже на мусор, и особенно не делайте этого в случайные отверстия или шахты, которые вы можете встретить. Хотя шансы невелики, вы понятия не имеете, может ли там быть куча невинных спелеологов внизу, которые не оценят дополнительную опасность ракет сверху).

Первое приближение

Старшая школа Физика вооружает нас простыми уравнениями движения. Гравитация (и, следовательно, ускорение) для свободно падающего камня постоянны. Мы можем использовать надежное уравнение:

Если мы будем осторожны, чтобы не дать камню никакой начальной скорости (мы бросим его в колодец, а не бросим туда), то u = 0 . Если мы уроним камень из положения, параллельного земле, смещения не будет. Срок разгона всего g .

Использование значения g = 9,81 м/с/с мы получаем приближение, что с ≈ 165 м

Наше первое приближение для глубины колодца составляет 165 м , вам может быть интересно узнать, что самая глубокая вырытая вручную (в отличие от пробуренной) скважина в мире — это водяная скважина Вудингдин в Брайтоне, Великобритания. На раскопки ушло четыре года с 1858 по 1862 год, а глубина составляет 390 м (такая же глубокая, как высота Эмпайр Стейт Билдинг! Это ошеломляюще глубоко!)

Изображение: synx508

(на фото выше не колодец Вудингдин, а колодец глубиной 200 футов в Грейс Корт в Оксфордшире, Великобритания).

Скорость звука

Это не так просто, как расчет выше.

Свет распространяется довольно быстро, а звук нет. Всплеск, который вы слышите, когда камень ударяется о воду, на самом деле является волной давления, которая проходит через воздух (поверхность воды вибрирует, что вызывает колебания воздуха, касающегося ее, которая вызывает колебания воздуха, касаясь ее…) Эти волны давления распространяются на скорость звука (определение того, что это значит!) При 20°C скорость звука составляет 343 м/с.

Вы слышите всплеск, задержанный на время, необходимое для того, чтобы звук удара дошел до вашего уха. Задержка пропорциональна глубине скважины.

Время, которое мы фиксируем на секундомере, представляет собой комбинацию времени падения камня плюс времени, необходимого звуку для достижения поверхности. Наши простые расчеты переоценивают глубину колодца, потому что все время приписывают только падению. Давайте исправим это.

Мы определим скорость звука как c . Таким образом, время, за которое звук достигает поверхности, равно с/с .

Истинное время, которое нам нужно интегрировать, чтобы получить расстояние падения, это время, когда мы слышим всплеск, вычесть время, за которое звук достигнет нас. Подставляя это, собирая члены, решая квадратное уравнение и извлекая разумный корень, мы получаем следующую формулу для глубины колодца.

Подстановка значений: g = 9,81 м/с/с, c = 343 м/с, t = 5,8 с , мы получаем обновленную оценку, что с ≈ 142,3 м .

Не учитывая скорость звука, мы завысили глубину скважины почти на 23 м

Табличные данные

Вот таблица, показывающая истинную высоту скважины (левая колонка), время падения породы в свободном падение, время возврата звука и общее время (по показаниям секундомера). В следующем столбце показано, что предложила бы глубина, если бы мы проигнорировали скорость звука, а последний столбец — это дельта (насколько она была бы пересчитана).

	Глубина скважины (м)	Время свободного падения (с)	Возврат звука (с)	Измеренное время (с)	Простая оценка глубины (м) 9007 7	Дельта (м)
	10	1,428	0,029	1,457	10,413	0,413
	20	2,019	0,058	2,078	21,172	1,172
	30	2,473	0,087	2,561	32,159	2,159
	40	2,856	0,117	2,972	43,334	3,334
	50	3,193	0,146	3,339	54,670	4,670
	60	3,497 900 94	0,175	3,672	66,152	6,152
	70	3,778	0,204	3,982	77,767 9 0094	7,767
	80	4,039	0,233	4,272	89,507	9,507
	90	4,284	0,262	4,546	101,364	11,364
9 0093 100	4,515	0,292	4,807	113,331	13,331
	110	4,736	0,321 9009 4	5,056	125,403	15,403
	120	4,946	0,350	5,296	137,576	17,576
	130	5,148	0,379	5,527	149,846	1 9,846
	140	5,342	0,408	5,751	162,209	22,209
	150 9 1 60	5,711	0,466	6,178	187,203	27,203
	170	5,887	0,496	6,383	199,829	29,829
	180	6,058	0,525	6,583	212,537	32,53 7
	190	6,224	0,554	6,778	225,326	3 5. 326
	200	6,386	0,583	6,969	238,194	38,194

Пока звук распространяется напрямую пропорционально глубине скважины, скорость породы увеличивается, и это вызывает изменения, пропорциональные квадрату времени. Чем глубже скважина, тем больше растет эта ошибка. Вот график, показывающий расчетную глубину скважины (ось Y) в зависимости от времени (ось X) для двух моделей.

Вы можете видеть, что простая модель постоянно переоценивает глубину, поскольку считает, что время, за которое звук поднимается вверх, равно времени, в течение которого камень все еще падает.

Реклама:

Перетащите

Пойдем дальше по кроличьей норе. Камень не падает в вакууме, а движется сквозь воздух. Воздух представляет собой плотную жидкость и придает камню сопротивление. На малых скоростях уместно не обращать внимания на лобовое сопротивление, но с увеличением скорости мы не можем позволить себе такой роскоши (помашите рукой перед лицом, и вы не почувствуете никакого сопротивления, но высунете руку из окна автомобиля). автомобиль едет со скоростью шоссе, и вы, конечно, можете!).

Сопротивление пропорционально квадрату скорости.

Здесь ρ — плотность воздуха, S (в данном случае заглавная S) — площадь смачивания, v — скорость, C _D — коэффициент сопротивления (у аэродинамически гладких форм меньше коэффициенты аэродинамического сопротивления, у более тупых форм они выше).

По мере того, как камень ускоряется вниз по шахте и его скорость увеличивается, он ощущает все большее и большее сопротивление воздуха. Сопротивление противодействует силе тяжести, уменьшая результирующую направленную вниз силу.

Из Ньютона II мы получаем следующее соотношение между силами и ускорением:

Конечная скорость

Здесь стоит сделать небольшое отступление, чтобы поговорить о концепции конечной скорости , потому что это интересно, но также и потому, что это позволит нам упростить математику чуть позже.

По мере увеличения скорости свободно падающего объекта в жидкости увеличивается и его сопротивление (пропорционально квадрату скорости). В конце концов эта сила сопротивления увеличивается, пока не сравняется с силой гравитации. Когда это происходит, на тело не действует результирующая сила, и оно перестает ускоряться. Вне любой внешней силы он не станет быстрее. Дошло до конечная скорость . Обозначим эту скорость как v _t .

Из этого уравнения видно, что чем ниже плотность воздуха (большая высота), тем выше конечная скорость, и чем ниже коэффициент лобового сопротивления, тем выше конечная скорость. Более массивные объекты также имеют более высокие конечные скорости.

Парашютисты, выпрыгивая из самолетов, быстро достигают предельной скорости в свободном падении. Изменяя свою позу (форму), они могут изменять свой коэффициент лобового сопротивления (и площадь поперечного сечения) и регулировать свою скорость и, таким образом, скорость снижения: раскинув руки и ноги в стороны, они получают высокий коэффициент лобового сопротивления, но прижимая руки к бокам и опуская голову, они становятся аэродинамически более плавными и ускоряются. Парашютист в стабильном положении на животе имеет конечную скорость около 120 миль в час (чуть более 50 м/с). Опускание головы и подгибание может увеличить эту скорость примерно до 180 миль в час.

Я никогда не прыгал с парашютом; это не то, что мне нравится, поэтому я все еще принадлежу к группе людей, чье общее количество взлетов за всю жизнь = общему количеству посадок (иногда меньше на единицу, если я нахожусь в середине полета! ), но мне сказали, что в свободном падении вы не чувствуете, что падаете (да и зачем?, на вас не действуют никакие чистые силы; это должно ощущаться так же, как лежание на кровати).

Когда парашютист раскрывает свой парашют, происходит значительное увеличение сопротивления, и это снижает конечную скорость настолько, чтобы обеспечить безопасную скорость приземления.

Спортивные мячи

Конечная скорость мяча для бейсбола и гольфа составляет около 33 м/с (75 миль/ч)*. Мелкие градины летят со скоростью 14 м/с (30 миль в час), а капли дождя — со скоростью 9 м/с (20 миль в час).

*Интересно, что при ударе очень опытным игроком начальная скорость мяча для гольфа может достигать 220 миль в час, а профессиональный бейсболист может подать мяч со скоростью более 100 миль в час. В обоих этих случаях мяч ускоряется внешними силами, и как только контакт с мячом теряется, чистая сила начинает замедлять мяч (о, и если вы собираетесь попасть в мяч для гольфа, это лучше, чтобы это произошло в конце пути, а не в начале!)0003

Связь между массой, площадью и сопротивлением, а также конечной скоростью объясняет, почему маленькие грызуны могут пережить огромные падения почти невредимыми. Есть замечательная цитата из статьи «О правильном размере » великого ученого Дж.Б.С. Холдейн (Халдин объединил теорию эволюции Дарвина с законами наследственности Менделя и был одной из самых ярких фигур в генетике 20-го века, опытным статистиком и ученым).

«Для мышей и любых мелких животных гравитация практически не представляет опасности. Вы можете бросить мышь в шахту длиной в тысячу ярдов; и, достигнув дна, он получает легкий толчок и уходит, при условии, что земля достаточно мягкая. Крысу убили, человека сломали, лошадь забрызгала». — Дж.Б.С. Холдейн

(Как бы ни был захватывающий звук всплеска лошади, пожалуйста, не бросайте в шахту никакие живые предметы!) и сосредоточив внимание только на падающей части времени, мы получим уравнение:

Разделив переменные, мы получим

Перестроив формулу для конечной скорости и подставив

, мы получим

Ссылаясь на нашу таблицу стандартных интегралов, мы помни, что

Мы получаем следующее решение:

Это интересный результат, показывающий, что математически конечная скорость никогда не достигается полностью. Мы просто продолжаем подходить ближе, и ближе, и ближе (очень быстро, неизмеримо близко). Это то, что мы ожидаем с чисто математической точки зрения.

Проинтегрировать снова

Чтобы уменьшить расстояние, проинтегрируем еще раз (снова сверившись с нашей таблицей стандартных интегралов и вспомнив tanh(x)=sinh(x)/cosh(x) ).

Соединяя все это вместе и прибавляя временные задержки для скорости звука, мы получаем:

Что слишком сложно для решения s , поэтому вместо этого мы просто решим численно. Давайте также использовать некоторые реальные цифры.

Представим, что наша скала представляет собой сферический кусок гранита размером с мрамор и диаметром 2 см. Плотность гранита составляет около 2,75 г/см ³ , поэтому этот камень будет весить ок. 11,5 г = 0,0115 кг. Его площадь поперечного сечения составляет 3,14 см 9 .0486 2 = 0,000314 м ² . При 20 °C плотность воздуха составляет 1,2 кг/м ³ , а грубое приближение коэффициента сопротивления для сферы равно C _D = 0,4

. Подстановка этих значений дает расчетную конечную скорость камня как ок. 38,7 м/с (87,1 мили в час)

Вот график зависимости смещения камня от времени (на том же графике нанесено простое приближение, основанное на уравнениях движения). Вы можете видеть, что кривая, учитывающая сопротивление воздуха, выравнивается и становится почти прямой линией, когда она приближается к конечной скорости (и, следовательно, к постоянной скорости). Из-за аэродинамического сопротивления и его воздействия на относительно легкую породу расстояние, которое он проходит за 5,8 секунды, составляет всего 118,6 м, а не 165 м, предсказываемые простой моделью (и это до того, как мы добавим модификацию на время задерживать).

Если вместо гальки мы бросили в колодец* чугунное пушечное ядро, то при радиусе 10 см и плотности 7,13 г/см ³ оно будет иметь массу 29,9 кг, что дает терминал скорость 197 м/с (441 миль/ч). Эта конечная скорость настолько высока, что сопротивлением можно пренебречь по сравнению с таким коротким расстоянием, поэтому кривые очень похожи.

Если бы мы уронили перо вниз, мы, вероятно, успели бы заварить чашку чая до того, как оно упадет в воду!

*Должен ли я напомнить вам, что не стоит бросать ядра в колодцы?

Собираем все вместе

Ниже приведен окончательный график, показывающий взаимосвязь между высотой колодца и временем, которое потребуется, чтобы услышать всплеск, с учетом квадратичного сопротивления ветра и задержки распространения звука, поднимающегося со дна. для небольшой сферической гальки гранита (я поменял местами оси на этой диаграмме).

На том же графике нанесено простое приближение, которое дают основные уравнения движения. Это довольно большая разница.

Использование числовых методов (я только что использовал Excel) для полной модели дает оценку глубины 114,9 м. 0,34 с. Интересно, что поскольку конечная скорость ограничивает скорость падения камня, это уменьшает ошибку, вызванную неприменением временной задержки.

Воздействие на самую глубокую скважину

Доведя это до предела, если бы мы бросили наш камешек в 390-метровую водяную скважину Вудингдин, мы не ожидали бы услышать всплеск, пока не истечет 12,8 секунды (и 1,13 секунды из этого времени были бы временем потребовалось, чтобы звук вернулся обратно в колодец).

Попробуйте посчитать это в уме. Это действительно глубокий колодец!

Рабочий лист: Вертикальное движение под действием силы тяжести

Начать практику

В этом рабочем листе мы попрактикуемся в использовании кинематических уравнений равномерного ускорения для моделирования вертикального движения тела с равномерным ускорением под действием силы тяжести.

Q1:

В колодец был брошен камень со скоростью 2 м/с. Он достиг дна за 1,5 секунды. Определить глубину 𝐷 колодца, учитывая, что ускорение свободного падения 90,8 м/с ² .

Q2:

Если яблоко падает с дерева и требуется 1,5 секунды, чтобы достигнет земли, с какой скоростью он ударится о землю? Возьмем ускорение за счет гравитация 𝑔=9,8/мс.

Q3:

Тело бросили вертикально вверх со скоростью 18,3 м/с. с высоты 163 м над землей. Найдите положение тела 5 секунд после того, как он был спроектирован. Возьмем 𝑔=9,8/мс.

Q4:

Заполните пропуск: Если тело брошено вертикально вверх со скоростью 𝑉 до максимальной высоты ℎ, тогда скорость, с которой тело должно быть отброшено, чтобы достичь высоты 4ℎ, равна .

• A4𝑉
• Б√2𝑉
• С𝑉
• D2𝑉

Q5:

Если тело, выпавшее из здания, заняло 3 секунды чтобы достичь земли, найти его среднюю скорость в момент падения. Пусть ускорение свободного падения 𝑔=9,8/мс.

Q6:

Тело бросили вертикально вниз с вершины башни высотой 80 м. Учитывая, что за 1-ю секунду своего движения он прошел 35,9 м, найдите время, необходимое для достижения земли, округленное до ближайших двух знаков после запятой. Пусть ускорение свободного падения 𝑔=90,8/мс.

Q7:

Частица брошена вертикально вверх со скоростью 7 м/с из точки на высоте 38,7 м. выше земли. Найдите максимальную высоту, на которую может подняться частица от земли. Рассмотрим ускорение свободного падения равно 9,8 м/с ² .

Q8:

Частица была брошена вертикально вверх с земли. Учитывая, что максимальная высота, которую достигла частица, была 62,5 м, найти скорость, с которой он был брошен. Возьмем ускорение свободного падения 𝑔=90,8/мс.

Q9:

Тело упало вертикально с вершины башни. За последнюю секунду до удара о землю он преодолел 86,73 м.