ПЗСМ — Воздуховоды
%data getProperty(72, ‘header_pic’, ‘view_right’)% ТОО ПЗСМ изготавливает спиральнонавивные воздуховоды оцинкованные, нержавеющие из рулонного штрипса шириной 137 мм и толщиной 0,5мм — 1мм. Спиральнонавивные воздуховоды изготавливаются на оборудовании фирмы «Spiro International Group» (Швейцария) без нарушения цинкового покрытия на фальцевом соединении! Производственная мощность составляет: 525 000 м.п. в год.
Область применения
Спиральнонавивные воздуховоды используются для любых видов вентиляции.
Преимущества
Благодаря надежности и высокому качеству фальцевых соединений воздуховодов, конструкции фасонных частей и герметичности ниппельного соединения уменьшаются утечки воздуха и потери давления в системе вентиляции, улучшаются шумовые характеристики системы.
Круглые воздуховоды максимально эффективны при проектировании систем вентиляции и монтаже воздуховодов оцинкованных. Прямоугольный оцинкованный воздуховод может быть заменен на круглый воздуховод без увеличения створа прохода воздуховодов.
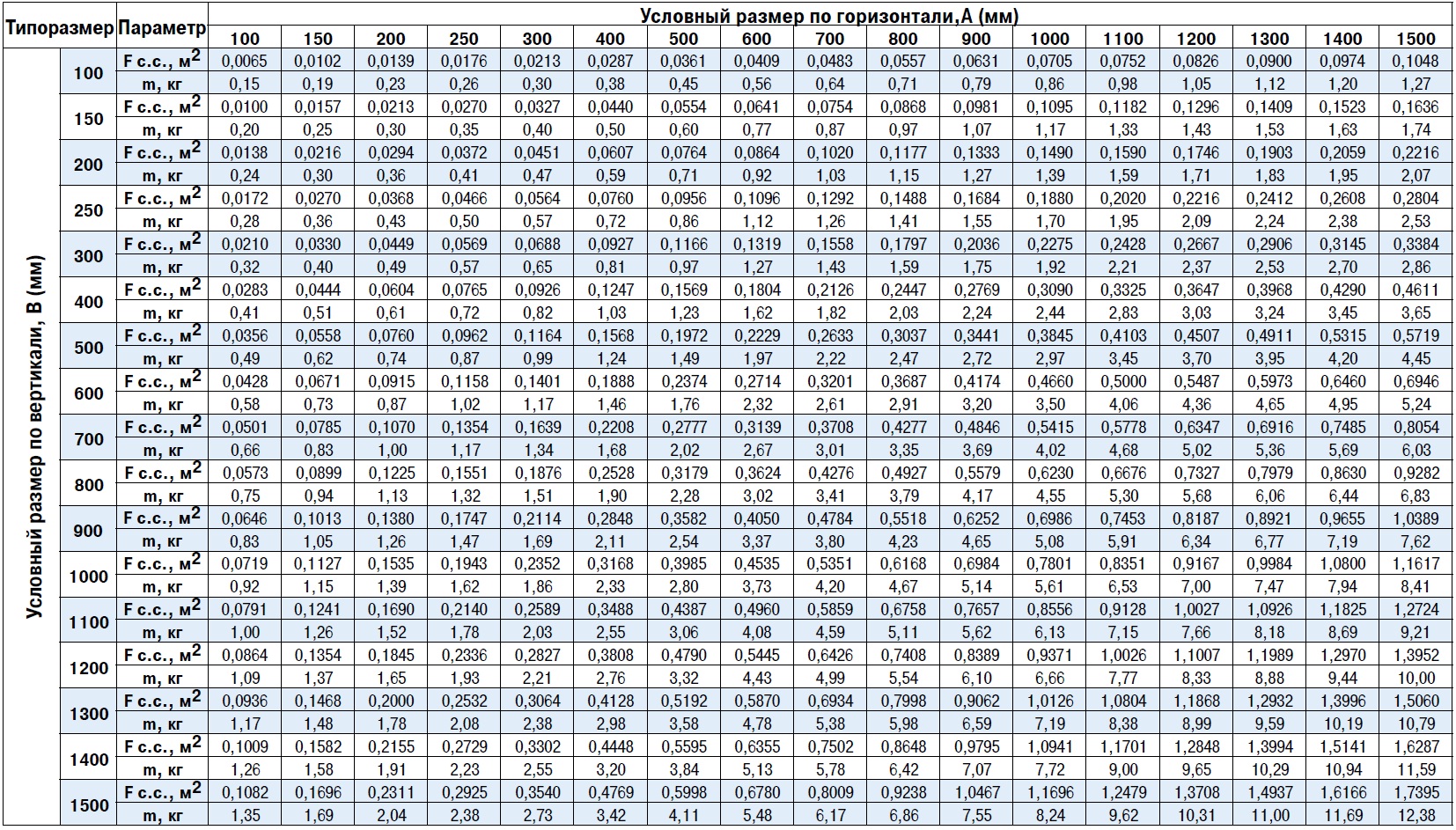
Всегда конструкция круглых воздуховодов занимает меньше пространства, чем соответствующие по площади сечения прямоугольного воздуховода. Площадь поверхности воздуховода оцинкованного круглой формы на 12% меньше соответствующей площади поверхности аналогичного сечения прямоугольного воздуховода. Для тепловой и противопожарной изоляции круглых воздуховодов достаточно более тонкого слоя изоляции, чем для прямоугольного при разных требованиях. Значительно сокращается объем требуемого теплоизоляционного материала. %data getProperty(77, ‘header_pic’, ‘view_left’)%
| Диаметр воздуховода | Толщина штрипса |
| 125 мм | 0,5 мм |
| 140 мм | 0,5 мм |
| 160 мм | 0,5 мм |
| 180 мм | 0,5 мм |
| 200 мм | 0,5 мм |
| 225 мм | 0,5 мм |
| 250 мм | 0,5 мм |
| 315 мм | 0,5 мм |
| 400 мм | 0,5 мм |
| 450 мм | 0,5 мм |
| 560 мм | 0,7 мм |
| 710 мм | 0,7 мм |
| 800 мм | 0,7 мм |
| 900 мм | |
| 1000 мм | 1 мм |
| 1100 мм | 1 мм |
| 1200 мм | 1 мм |
Список прайс-листов
ООО Профвент (Пермь) — официальный сайт производителя
«Профессиональная вентиляция» – это предприятие производящее вентиляционную продукцию, используемую для монтажа систем вентиляции, кондиционирования, систем дымоудаления (класса «Н» и «П»), аспирации и пневмотранспорта.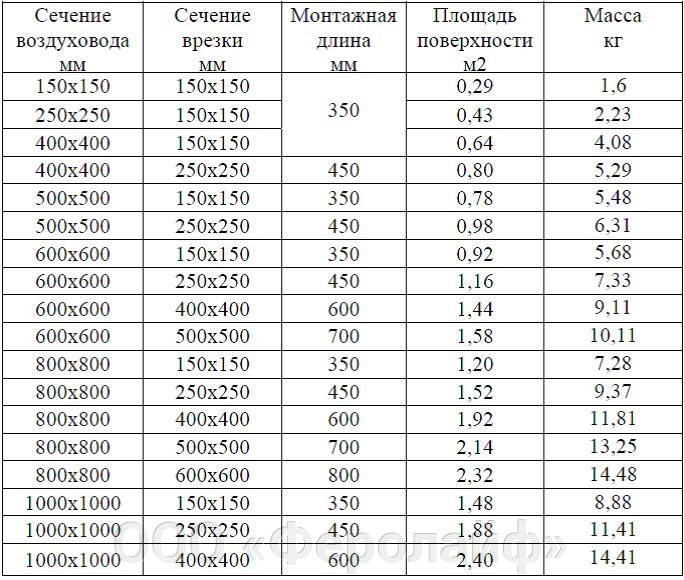
Основанное в 2008 году, сегодня «ПРОФВЕНТ» имеет производственные мощности до 200 000 м 2 в год. Кроме воздуховодов мы обеспечиваем комплексные поставки оборудования и комплектующих, включая: изоляцию и огнезащиту; вентиляционные решетки и диффузоры; утепленные воздуховоды; обратные и противопожарные
клапана; вентиляторы и калориферы; метизы и крепеж; непрофильные изделия и многое другое. На производстве применяется уникальное высокотехнологичное оборудование, которое позволяет изготавливать продукцию высокого качества в кратчайшие сроки.
год образования
компаний «Профвент»
м2 воздуховодов
мы произвели
м2 мы произвели
фасонных частей
мы произвели
клапанов
мы произвели
единиц оборудования
ОСНОВНЫМИ НАПРАВЛЕНИЯМИ ПРОИЗВОДСТВА ЯВЛЯЮТСЯ:
Воздуховоды и фасонные части круглого и прямоугольного сечения из оцинкованной, нержавеющей стали и цветных металлов толщиной от 0.5 до 1.2 мм.
Круглые воздуховоды спирально-навивные и прямошовные изготавливаются длиной 3000 (6000) мм и 1250 (2000) мм соответственно.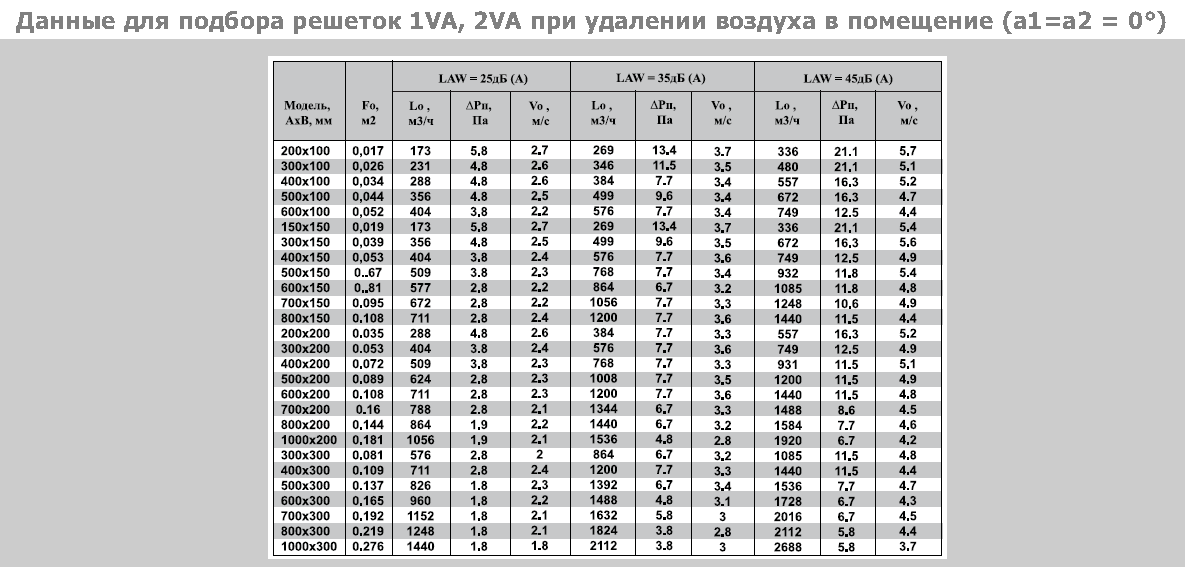
Прямые участки прямоугольных воздуховодов изготавливаются на автоматической линии стандартной длиной 1250 мм. Так же возможно изготовление нестандартных воздуховодов по эскизу заказчика длиной до 2500 мм.
Сварные воздуховоды прямоугольного и круглого сечения из металлов от 1,2 мм до 2 мм. Воздуховоды диаметром от 100 мм до 140 мм производятся толщиной от 0.5 мм до 1.2 мм и до 2мм диаметром свыше 140 мм. Стандартная длина воздуховодов 1250 мм, но возможны отклонения от стандартной длины воздуховодов после согласования. Сварные швы выполняются в соответствии с требованиями ГОСТ 3242-79. Все сварные швы после сварки зачищают абразивными инструментом от шлака и окалины. Изделия изготовленные из чёрной стали покрываются грунтовкой
ГФ-021 по ГОСТ 25129-89.
При изготовлении используется ручная и полуавтоматическая дуговая сварка.
Гибка листовых металлов на станке с ЧПУ.
Вальцовка рулонного и листового металла.
Производство металлоконструкций методом вальцевания, для изготовления труб, сегментов, конусов и емкостей различного диаметра.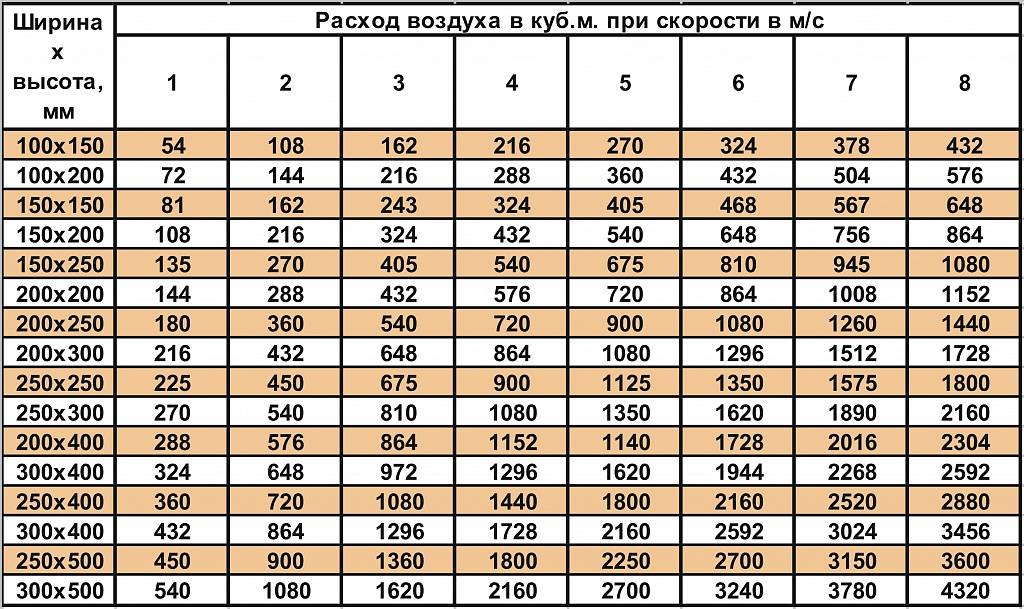
Лазерная резка на станке с ЧПУ.
Раскрой металла по индивидуальному эскизу заказчика толщиной до 3 мм. Стандартные габаритные размеры рабочей поверхности 3000х1500 мм.
Укажите контакты куда отправить наш полный прайс и каталог
Электронная почта
Номер телефона
ТЕХНИЧЕСКИЙ КОММЕНТАРИЙ
СООТВЕТСТВИЕ СНИП
Мы соберём для Вас различные варианты комплектации систем вентиляции по вашей спецификации. Согласно СНиП 41-01-2003 «Отопление, вентиляция и кондиционирование» для монтажа вентиляционных систем рекомендуется применение круглых воздуховодов. Прямоугольные воздуховоды рекомендуется применять только при специальном обосновании, там, где невозможно конструктивно пройти воздуховодами большого круглого сечения (строительные фермы, балки и т. д.) или же заменить большое сечение круглого воздуховода на два или три параллельно идущих круглых воздуховода меньшего сечения
ЭКОНОМИЯ
Стоимость воздуховодов определяется площадью.
площади поверхности аналогичного по живому сечению прямоугольного воздуховода, а при отношении сторон
прямоугольного воздуховода 1:4 разница возрастает до 40 %. Это делает эффективным замену одного прямоугольного
воздуховода на несколько круглых, идущих параллельно. Помимо этого, чем меньше периметр прямоугольного
воздуховода, тем больше удельная (на 1 м2 поверхности воздуховода) стоимость фланцев и крепежа для его монтажа.
КАЧЕСТВО
Наш завод, применяя современную технологию и оборудование, в минимальные сроки изготовит воздуховоды и
фасонные части, соответствующие стандарту качества.
Воздуховоды (спирально-навивные) и фасонные части диаметром до 315 мм всегда имеются в наличии на складе.
| Определение
Создано Богной Шик и Ханной Памула, докторами наук
Отредактировано Стивеном Вудингом и Джеком Боуотером
Последнее обновление: 05 июня 2023 г.
- Что такое площадь поверхности? Определение площади поверхности
- Формула площади поверхности…
- Площадь поверхности сферы
- Площадь поверхности цилиндра
- Площадь поверхности конуса
- Площадь поверхности куба
- Площадь поверхности пирамиды
- Площадь поверхности прямоугольной призмы
- Площадь поверхности треугольной призмы
- Площадь поверхности тела
- Как рассчитать площадь поверхности сферы?
- Прочие вопросы
- Часто задаваемые вопросы
Этот калькулятор площади поверхности поможет вам найти площадь наиболее распространенных трехмерных тел . Если вы когда-нибудь задавались вопросом, как найти площадь поверхности или что такое площадь боковой поверхности, этот калькулятор здесь, чтобы помочь вам. Площадь поверхности имеет гигантский список приложений в каждой области, например, в аэродинамике.
В этой статье вы найдете формулы площади поверхности сферы, куба, цилиндра, конуса, пирамиды и прямоугольной/треугольной призмы.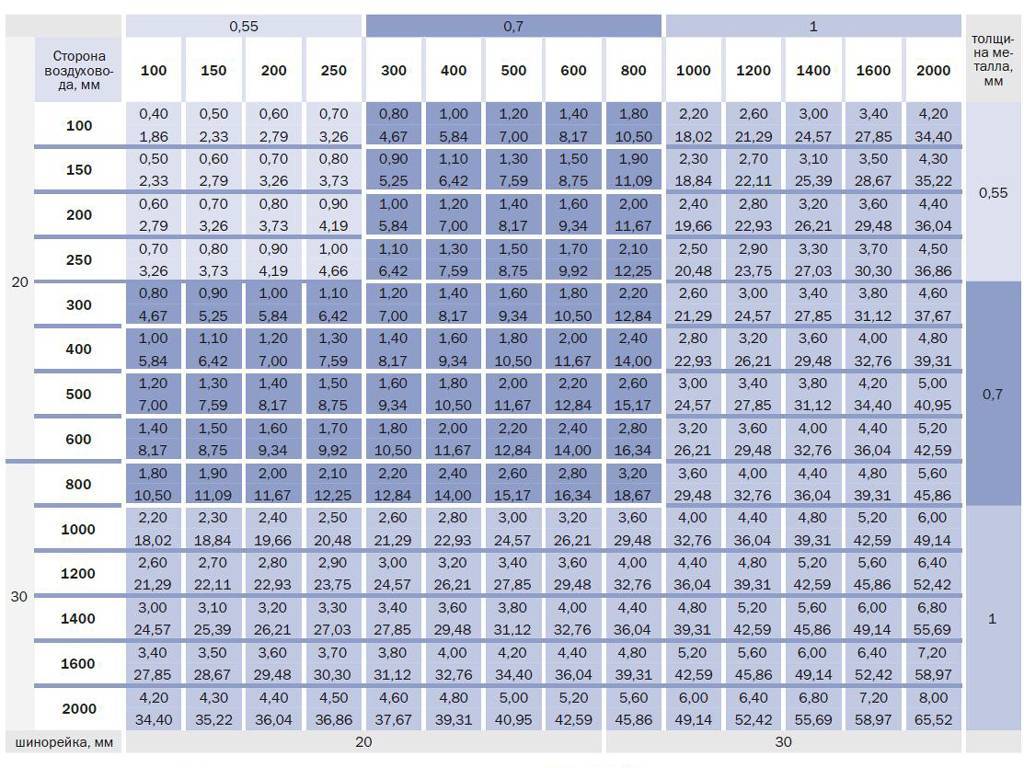
Мы также объясним, как рассчитать площадь поверхности сферы в качестве примера.
Что такое площадь поверхности? Определение площади поверхности
Площадь поверхности равна общей площади, которую занимает поверхность объекта . Другими словами, это общая площадь поверхности 3D-объекта.
Иногда площадь поверхности можно разделить на сумму площадь основания и площадь боковой поверхности . Боковая поверхность – это площадь всех сторон объекта, исключая его основание и вершину. Это деление используется для форм, в которых существует очевидное различие между основанием и другой частью, например, для цилиндра, конуса, пирамиды или треугольной призмы. Он редко применяется к твердым телам, для которых мы не уверены, какие грани следует рассматривать как основания (например, в кубе или параллелепипеде), и мы не используем его для гладких поверхностей, таких как сфера.
Формула площади поверхности…
Наш калькулятор площади поверхности может найти площадь поверхности семи различных твердых тел.
Формула зависит от типа твердого вещества.Площадь поверхности сферы:
A = 4πr², где r — радиус сферы.Площадь поверхности куба:
A = 6a², где a — длина стороны.Площадь поверхности цилиндра:
A = 2πr² + 2πrh, где r — радиус, а h — высота цилиндра.Площадь поверхности конуса:
A = πr² + πr√(r² + h²), где r — радиус, а h — высота конуса.Площадь поверхности прямоугольной призмы (коробки):
A = 2(ab + bc + ac), где a , b и c — длины трех сторон прямоугольного параллелепипеда.Площадь поверхности треугольной призмы:
A = 0,5 × √((a + b + c) × (-a + b + c) × (a - b + c) × (a + b - c)) + h × (a + b + c), где a , b и c — длины трех сторон основания треугольной призмы, а h — высота (длина) призмы.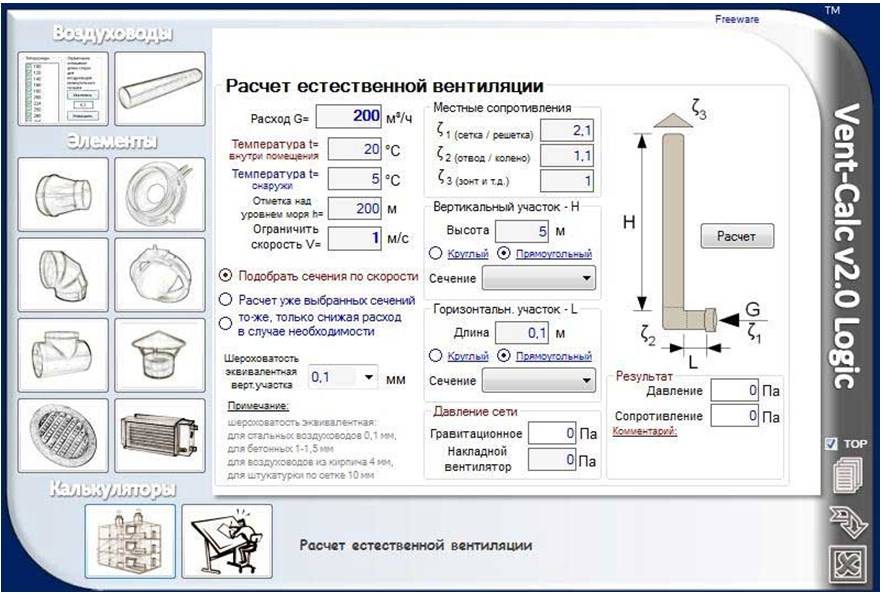
Площадь поверхности пирамиды:
A = l × √(l² + 4 × h²) + l², где l — длина стороны квадратного основания и ч — высота пирамиды.
Но откуда берутся эти формулы? Как найти площадь поверхности основных трехмерных фигур? Продолжайте читать, и вы узнаете!
Площадь поверхности сферы
Чтобы вычислить площадь поверхности сферы, все, что вам нужно знать, это радиус сферы или ее диаметр.
-
A = 4 × π × r², гдеr— радиус.
Как мы знаем, диаметр шара равен двум радиусам d = 2r , мы можем преобразовать уравнение в другую форму:
-
A = 4 × π × (d / 2)² = π × d², гдеd— диаметр сферы.
Вывод этой формулы площади поверхности требует интегрирования. Если вам интересно, посмотрите это доказательство.
Площадь поверхности цилиндра
Чтобы узнать площадь поверхности цилиндра, необходимо иметь две величины: радиус (или диаметр) основания и высоту цилиндра.
Общее уравнение как обычно — площадь основания
-
А = 2πr² + 2πrh
Откуда взялась эта формула? Вы можете написать уравнение для площади поверхности цилиндра как:
-
A = A(боковая) + 2 × A(основная)
Площадь основания найти легко — помним известную формулу площади круга: A(основание) = π × r² . Но какова форма площади боковой поверхности? Попробуйте представить, что мы его «разворачиваем». Вы признаете это? это прямоугольник ! Длина одной стороны — это высота цилиндра, а вторая — длина окружности в развернутом виде.
-
А(основание) = π × r² -
A(поперечный) = h × (2 × π × r)
Площадь поверхности конуса
Мы можем разделить площадь поверхности конуса на две части:
-
A = A(боковая) + A(основание), так как у нас есть только одно основание, напротив к цилиндру.
Основание снова равно площади круга A(основание) = π × r² , но происхождение площади боковой поверхности может быть не столь очевидным:
-
A(боковая) = π × r × √(r² + h²)
Давайте посмотрим на этот пошаговый вывод:
Раскатайте боковую поверхность до плоского состояния. Круговой сектор, являющийся частью окружности радиусом s ( s высота наклона конуса).
Для круга с радиусом s, длина окружности равна
2 × π × с. Длина дуги сектора равна2 × π × r.Площадь сектора , который является нашей боковой поверхностью конуса, определяется по формуле:
A(поперечный) = (s × (длина дуги)) / 2 = (s × 2 × π × r) / 2 = π × r × sФормулу можно получить из пропорций, так как отношение площадей фигур такое же, как отношение длины дуги к длине окружности:
(площадь сектора) / (площадь большого круга) = (длина дуги) / (длина большого круга), поэтому:(площадь сектора) / (π × с²) = (2 × π × r) / (2 × π × с)(площадь сектора) = (π × с²) × (2 × π × r) / (2 × π × с)A(поперечный) = π × r × sЧтобы найти недостающий член этого отношения, вы также можете попробовать наш калькулятор отношений!
- Обычно у нас нет
sзадано значение, ноh, что равно высоте конуса. Но это совсем не проблема! Мы можем легко преобразовать формулу, используя теорему Пифагора:
Но это совсем не проблема! Мы можем легко преобразовать формулу, используя теорему Пифагора:r² + h²= s², извлекая квадратный корень, получаемs = √(r² + h²)Таким образом, формула площади боковой поверхности выглядит следующим образом:
A(поперечный) = π × r × √(r² + h²)
- Наконец, сложите площади основания и боковой части, чтобы найти окончательную формулу площади поверхности конуса :
-
A = A(поперечный) + A(основной) = π × r × s + π × r²заданоrиsили -
A = π × r × √(r² + h²) + π × r²учитываяrиh.
Площадь поверхности куба
Площадь поверхности куба проще всего представить: каждая из сторон представляет собой квадрат! Поскольку каждый куб имеет шесть одинаковых квадратных граней, площадь поверхности равна:
-
A = 6 × (боковая часть)
Так как площадь квадрата является произведением длины его сторон, окончательная формула для площади поверхности куба будет следующей:
-
A = 6 × l², гдеl— квадрат сторона
Площадь поверхности пирамиды
Пирамида представляет собой трехмерное тело с многоугольным основанием и треугольными боковыми гранями.
Когда вы слышите пирамида , обычно предполагается, что обычная квадратная пирамида . Но в зависимости от формы основания, это могла быть и шестиугольная пирамида, и прямоугольная пирамида. Обычный означает, что он имеет основание правильного многоугольника и представляет собой правильную пирамиду (вершина прямо над центроидом его основания), а квадрат – означает, что он имеет эту форму в качестве основания. Это вариант, который мы использовали в качестве пирамиды в этом калькуляторе площади поверхности.
Формула площади поверхности пирамиды:
-
A = l × √(l² + 4 × h²) + l²гдеlсторона основания, аhвысота пирамиды
Опять же, мы можем разделить уравнение на:
A = A(основание) + A(сторона) = A(основание) + 4 × A(боковая сторона)
Основание имеет форму квадрата , так что A (основание) = l² . Для расчета площади боковой поверхности начнем с площади одной треугольной грани:
Чтобы найти высоту треугольника, нам снова понадобится формула гипотенузы:
с = √(а² + b²)Вычислите гипотенузу треугольника ABC (которая одновременно является высотой треугольной грани):
c = √(h² + (l/2)²) = √(h² + l²/4)Площадь треугольника (в нашем случае это равнобедренный треугольник) можно вычислить как:
A = высота × основание / 2поэтомуA(боковая сторона) = √(h² + l²/4) × l / 2Итак, окончательная формула площади поверхности пирамиды:
A = l² + 4 × √(h² + l²/4) × l / 2 = l² + 2 × l × √(h² + l²/4)A = l² + l × √(4 × h² + l²)
Площадь поверхности прямоугольной призмы
Чтобы вычислить площадь поверхности прямоугольной призмы, достаточно вычислить площади сторон прямоугольника:
-
A = 2 × (A1 + A2 + A3)
где:
-
A1 = длина × ширина -
A2 = Ш × В -
A3 = Д × В
Таким образом, окончательная формула:
-
A = 2 × (l × w + w × h + l × h)
Площадь поверхности треугольной призмы
Чтобы понять, откуда берется формула площади поверхности треугольной призмы, давайте посмотрим на этот вывод:
Часть площади боковой поверхности в этом случае легко вычислить.
Как видно из рисунка, он состоит из трех прямоугольников с общей длиной одной стороны:A(боковой) = a × h + b × h + c × h = h × (a + b + c), который мы также можем записать вкратце как:
A(боковой) = h × P, гдеP— периметр базового треугольникаЗатем найдите площадь треугольного основания. Вы можете сделать это разными способами, в зависимости от того, что вам дано. В нашем калькуляторе мы реализовали расчет на основе формулы Герона — она используется, когда у вас есть три стороны треугольника (SSS).
A(основание) = 0,25 × √((a + b + c) × (-a + b + c) × (a - b + c) × (a + b - c)))Окончательная формула площади поверхности треугольной призмы:
A = A (боковой) + 2 × A (базовый)A = h × (a + b + c) + 0,5 × √((a + b + c) × (-a + b + c) × (a - b + c) × (a + b - c) ))
Как видно из рисунка, он состоит из трех прямоугольников с общей длиной одной стороны:Площадь поверхности тела
Вы можете рассчитать поверхность любого твердого тела, например, вашего тела — это не обязательно должна быть простая фигура из геометрии! Если вам интересно, какова площадь внешней поверхности человеческого тела, посмотрите этот калькулятор площади поверхности тела.
Как рассчитать площадь поверхности сферы?
Если вы хотите найти площадь поверхности сферы, вам необходимо выполнить следующие шаги:
Определить радиус сферы. Мы можем принять радиус 10 см.
Введите это значение в формулу:
А = 4πr²Рассчитать результат:
А = 4π × 10² = 1256 см²Вы также можете использовать онлайн-калькулятор площади поверхности, чтобы найти радиус сферы, если знаете ее площадь.
Прочие соображения
Единицами площади поверхности всегда являются квадратные единицы длины. Например, вы можете выразить его в см², дюймах², футах², м², а также в акрах и гектарах.
Если вы хотите найти объем любого из этих тел, воспользуйтесь нашим калькулятором объема.
Часто задаваемые вопросы
Как найти сторону куба по заданной площади?
Чтобы преобразовать площадь поверхности куба в длину его стороны, выполните следующие действия:
- Запишите площадь своего куба.
- Разделите на шесть . Результатом является площадь одного лица.
- Возьмите квадратный корень из числа из шага 2.
- Это длина сторон вашего куба . Отличная работа!
Как найти радиус сферы по заданной площади?
Чтобы определить радиус сферы по площади ее поверхности:
- Запишите площадь поверхности сферы.
- Разделите на
4π ≈ 12,566. - Возьмите квадратный корень из :
√(Площадь / 4π). - Вот и все; это радиус! Вы можете проверить свой результат с помощью онлайн-калькулятора площади поверхности.
Какова площадь поверхности цилиндра с радиусом и высотой, равными 2 дюймам?
Ответ: 50,2655 в кв. . Чтобы получить этот результат, вспомните, что формула площади поверхности цилиндра:
Площадь = 2πr(r + h)
Подставляя r = h = 2 , получаем Площадь = 16π ≈ 50,2655 .
Запомните единицы измерения! Так как r и h находятся в в , площадь равна в кв .
Богна Шик и Ханна Памула, PhD
Радиус (r)
Площадь поверхности
Площадь поверхности
Посмотреть 23 похожих калькулятора 3D-геометрии 📦
Площадь полушарияКуб Cube Calc: найти v, a, d… еще 20
Техническая информация
Duct Balloon®
Надувные изоляционные барьеры —
Дом Часто задаваемые вопросы ГТ/КУ СКВ/ДДГ Приложения Фотогалерея Связаться с нами Выставки
Каждый Duct Balloon® предназначен для конкретного применения в зависимости от размера воздуховода конечного пользователя, ограничений по пространству и условий установки.
Есть много элементов, которые диктуют возможности прогнозирования удержания, которые требуют физических испытаний и математического анализа.
Для закрепления Duct Balloon® в испытательной камере использовались два метода, показанные ниже. В одном методе использовалась стальная цепь, прикрепленная к стенке воздуховода, а затем к анкерным кольцам. Другой метод заключался в использовании стальной цепи между анкерными кольцами и закрепленными стальными опорными стержнями:
Крепится цепью между анкерными кольцами и воздуховодом
Крепится цепью и стальными стержнями внутри воздуховода
Примечание. опыт проектирования конструкций. Несоблюдение этого правила может привести к травме или смерти.
На приведенной ниже диаграмме показано, что различные значения удерживающей способности могут быть достигнуты за счет использования различной толщины периметра, а также различных методов крепления внутри воздуховода:
Программа испытаний показала, что прогнозируемые значения удержания могут варьироваться от 0,5 дюйма вод.
ст. (12,45 мбар) только за счет трения, но до 10 дюймов водяного столба. (24,9 мбар), если они должным образом закреплены в воздуховоде. Вообще говоря, чем больше размер Duct Balloon®, тем меньшее давление он будет удерживать до того, как начнет течь. Например, прогнозируемая удерживающая способность для размера 10 футов (3,04 м) в высоту, 10 футов (3,04 м) в ширину и 3 футов (0,09 м) в глубину с использованием одного нагнетателя высокого давления 120 В или 220 В, 2 л.с., выглядит следующим образом:
Фрикционный метод удержания
Давление в воздуховоде: 0,078 дюйма ч30 (0,19 мбар)
Усилие, нажимаемое на Duct Balloon®: 407 фунтов (184 кг) при данном давлении анкерные кольца
Давление в воздуховоде: 4,80 дюйма ч30 (11,9 мбар)
Силовое нажатие на воздуховод Balloon®: 2497 фунтов (1132 кг) при данном давлении 5,13 дюйм·ч30 (13,2 мбар)
Сила, нажимающая на Duct Balloon®: 2668 фунтов (1210 кг) при этом давлении
Следует понимать, что на точность этих прогнозируемых значений удерживания могут влиять несколько переменных, таких как размер Duct Balloon®, глубина периметра, выбор материала, состояние поверхности воздуховода, способ крепления Duct Balloon®, атмосферное давление, температура, количество используемых воздуходувок, а также общая целостность установки.
Если вы планируете установить Duct Balloon® в месте, где будет наблюдаться некоторый перепад давления, вам следует знать о методе «двойной блокировки и выпуска», который показан в художественной визуализации, нажав здесь. Всегда консультируйтесь с отделом безопасности вашей компании или ответственным лицом, прежде чем принимать решение об использовании ЛЮБОГО типа временного барьера!
Величина перепада давления, который Duct Balloon® может выдержать до того, как он сдвинется или протечет, зависит от метода, используемого для его установки в воздуховоде. Используя тестовую программу, разработанную Департаментом аэрокосмической техники Пенсильванского государственного университета, был проведен тщательный анализ путем тестирования тканей на коэффициент трения, а также обзора текущих конструкций продуктов. Поскольку их аэродинамическая труба представляла собой петлю и не могла использоваться, была построена специальная барокамера, рассчитанная на давление до 20 дюймов водяного столба.
(490,8 мбар) Изготовленные на заказ баллоны Duct Balloon® были поставлены различной глубины для испытательной камеры, которую можно было подключить к лабораторным приборам для измерения внешних и внутренних сил. Результаты, полученные в результате этого тестирования, основаны на следующих примечаниях и уравнениях:
Сила, необходимая для того, чтобы объект скользил по любой поверхности, называется силой трения (FF) и определяется как коэффициент трения (μ), умноженный на нормальный сила (FN) между двумя поверхностями:
При анализе Duct Balloon®, удерживаемого в воздуховоде за счет трения, сила трения (FF) должна быть равна или превышать силу давления (FD), воздействующую на передняя поверхность аэростата, если ожидается, что он останется неподвижным:
… минимальные требования, предъявляемые к Duct Balloon®, чтобы оставаться неподвижным
Сила давления (FD), конечно же, равна давлению (PD), умноженному на площадь поверхности (hw ) фронтальной части Duct Balloon® лицевая сторона:
Напротив, нормальная сила (FN) должна быть равна давлению баллона (PB), умноженному на площадь поверхности воздуховода, контактирующую с краем периметра Duct Balloon®.
Площадь поверхности воздуховода равна периметру воздуховода (2)(h+w), умноженному на глубину баллона (дБ).
Комбинируя вышеприведенные уравнения, минимальная необходимая взаимосвязь между давлением в воздуховоде и давлением Duct Balloon® для стационарного прямоугольного баллона представлена ниже в уравнении 1:
Если изменить эту формулу для учета воздуховодов круглого сечения поперечных сечений диаметром (D), он представлен ниже в уравнении 2:0003
Важно отметить, что отношение давления в воздуховоде к давлению в воздуховоде Duct Balloon®, таким образом, равно (μ) умноженному на отношение площади поверхности Duct Balloon®, контактирующей с воздуховодом, к площади передней поверхности.
FF = мкFN
| О нас |
| Статьи |
| Техническая информация |
| Отзывы |
| Как это работает |
| Таблица веса |
| Схема компоновки |
| Зоны деформационных швов |
| Точки крепления |
| Часто задаваемые вопросы о ГТ с котлами-утилизаторами |
| Установка выпускного канала газовой турбины |
| Установка баллона дымовой трубы котла-утилизатора |
| Быстро открывающаяся дверца доступа |
| Стек воздушный шар с вентиляционным отверстием |
| Неудачные фотографии демпфера стека |
| Статья CCJ «Воздушный шар сохраняет тепло котла-утилизатора» |
| Статья CCJ о награде за передовой опыт |
2006 г. |