Площадь сечения круглых воздуховодов таблица, формула
Принудительная вентиляционная система предусматривает использование круглых воздуховодов. Чтобы определить оптимальное количество материала, требуемого для создания подобной системы, необходимо рассчитать ее общую площадь. При подобном расчете учитываются такие показатели воздушных масс, как:
- — скорость;
- — объем.
Также необходимо принять во внимание величину пространства, где планируется монтаж вентсистемы. Диаметр будущих воздуховодов зависит от:
- — количества жильцов;
- — площади помещения.
Площадь круглых воздуховодов таблица (формула)
Во время проектирования помещения, специалистами вычисляется площадь круглого воздуховода. Проходка каналов выполняется внутри стен.
Однако площадь воздуховодов может быть измерена только после установления необходимого показателя производительности. Для этого нужно вычислить кратность воздухообмена с использованием рекомендуемых показателей СНиП.
Учитывается и количество людей, которые длительно или постоянно присутствуют в помещении. Полученный показатель площади воздуховода позволяет грамотно подобрать конфигурацию трубы.
Процесс расчета площади сечения круглых воздуховодов — формула
Круглый тип воздуховода иногда считается не совсем оптимальным выбором. Такие вентиляционные системы существенно снижают высоту помещений, особенно после установки потолков. Если увечить сечение канальной магистрали, тогда:
- — исчезнут акустические эффекты;
- — снизится скорость движения воздушных масс;
- — уменьшится шум.
При расчете площади специалисты пользуются масштабированным планом помещения. Он считается обязательным документом, чтобы создать детальную схему будущей вентиляционной системы. Подобная схема позволяет безошибочно установить воздуховоды, обеспечивающие:
- — подачу воздушных масс в помещении;
- — забор загрязненного воздуха;
- — вывод запахов.
Наиболее важным показателем в вентиляционных системах круглого сечения считается давление. Оно должно быть сбалансировано таким образом, чтобы не допустить распространения запахов из кухонных помещений в коридоры. Существуют нормативы СНиП, либо МГСН, по которым вычисляется данный показатель. В соответствии с полученными расчетами, выбираются следующие элементы будущей вентсистемы:
- — трубы воздуховода;
- — отводы;
- — переходники;
- — разветвители;
- — дифуззоры;
- — дроссели автоматические;
- — дроссели ручные;
- — решетки.
Каждый опытный специалист старается добиться минимальной длины каналов, обеспечивая при этом качественную подачу в здание воздушных масс. Круглые воздуховоды выбирают в соответствии с сечением, которое предопределяет объемы и скорость циркуляции воздуха. Уменьшение размера вызывает увеличение скорости. А это способствует появлению дополнительного шума.
Расчет вентиляции с помощью онлайн калькулятора
Материалы для скачивания
Рейтинг ↑ не забываем
Порядок действий при демонтаже кондиционеров (посмотреть)
Свод правил вентиляции и кондиционирования 2017 год (посмотреть)
Условные обозначения систем вентиляции и кондиционирования (посмотреть)
Требования к пожарной безопастности по вентиляции и кондиционированию (посмотреть).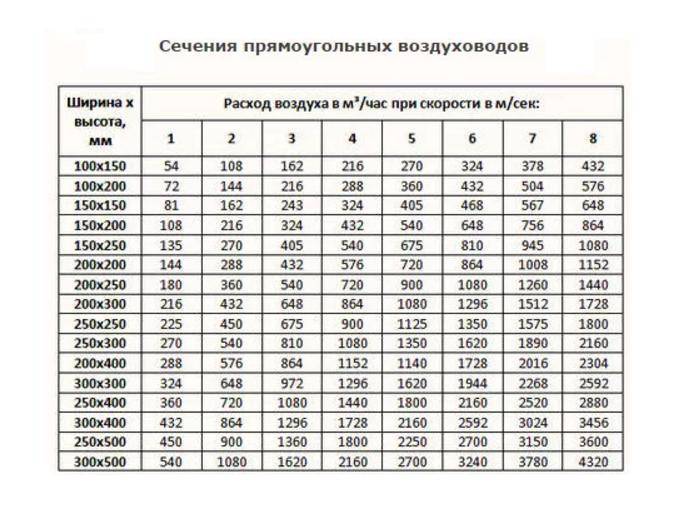
Ответы на задачи по технической механике
Если Вы не нашли свой вариант ответа, обращайтесь перейдя по ссылке в группу ВК опубликовав Ваши задачи прям в ленту группы ,по возможности постараемся Вам помочь. На данной странице не все ответы, перейдя по ссылке попадаете на другую страницу с ответами
Задача № 29 Найти реакцию опор
Ответ к задачи №29
Задача № 20 Натяжка троса
Ответ к задачи № 20
Задача №7 Найти реакцию опор
Ответ к задаче №7
Задача № 9 Распределение нагрузки
Ответ к задачи № 9
Задача № 11 Определить координаты центра тяжести сечения
Ответ к задачи № 11 С решением
Задача № 12 Найти реакцию опор
Ответ к задачи №12
Задача № 13 Решить графически
Ответ к задаче №13
Задача № 33 Решить графически
Ответ к задачи № 33
Задача № 33 Силы давящие на шар
Ответ к задачи № 33 Силы давящие на шар
Задача № Задача №21 Определить координат центра тяжести
Ответ к задаче № 21 Определить координат центра тяжести
Ответ № 21 /2 Определить координат центра тяжести 30А Ответ на координат центр тяжести № 21 -27
Задача № 20 Определить опорные реакции балки.
Проверить правильность их определения
Ответ к задачи № 20 Определить опорные реакции балки.Проверить правильность их определения
Задача № 22 Задача № 22 найти R(a) и R(b)
Ответ к задачи Задача № 22 найти R(a) и R(b)
Задача Определить координаты центра тяжести сечения.Показать положение центра тяжести на чертеже
Ответ к задачи Определить координаты центра тяжести сечения.Показать положение центра тяжести на чертеже
Задача № 10 Найти реакцию опор
Ответ к задачи №10 Найти реакцию опор
Задача № 16 Определить опорные реакции балки.Проверить правильность их определения
Ответ к задачи № 16
Задача № 22 Определить опорные реакции балки. Проверить правильность их определения
Ответ к задачи № 22 Определить опорные реакции балки Проверить правильность их определения
Задача № 27 Определить опорные реакции балки Проверить правильность их определения
Ответ к задачи № 27 Определить опорные реакции балки Проверить правильность их определения
Задача № 26 Определить опорные реакции балки Проверить правильность их определения
Ответ к задачи № 26 Определить опорные реакции балки Проверить правильность их определения
Вариант 32 задача № 1Определить опорные реакции балки на двух опорах.
Ответ к варианту 32 задача №1Определить опорные реакции балки на двух опорах. Проверить правильность их определения
Вариант 32 задача №2 Определить координаты центра тяжести сечения Показать положение центра на чертеже
Ответ к варианту 32 №2 Определить координаты центра тяжести сечения Показать положение центра на чертеже
Решение к варианту 32 № 2
Вариант 24 задача № 2 Определить координаты центра тяжести сечения Показать положения центра тяжести на чертеже
Ответ к варианту 24 задача № 2 Определить координаты центра тяжести сечения
Задача Указать положение центра тяжести на рисунке, придерживаясь определенного масштаба
Ответ к задачи Указать положение центра тяжести на рисунке, придерживаясь определенного масштаба
Задача — Определить величину и направления реакцию связей
Ответ к задаче -Определить величину и направления реакций связей
Задача- Определить опорные реакции балки на 2-х опорах
Ответ к задачи Определить опорные реакции балки на 2-х опорах
Задача № 9 Найти центр тяжести
Ответ к задаче № 9 найти центр тяжести
Найти центр тяжести
Решение к задаче Найти центр тяжести
Задача № 7
Решение к задаче № 7
28 задача Определить положение координаты центра тяжести
Ответ к 28 задачи Определить положение координаты центра тяжести
Задача Найти центр тяжести
Ответ к задаче Найти центр тяжести
Задача № 16 Определить положение координаты центра тяжести
Ответ к задаче № 16 Определить положение координаты центра тяжести
Ответ к задаче № 16 Определить положение координаты центра тяжести
Задача №23 Определить кординаты центра тяжести сечения
Ответ к задаче № 23 Определить координаты центра тяжести сечения
Определить опорные реакции балки
Ответ к задаче Определить опорные реакции балки
Определить опорные реакции балки
Ответ к задаче Определить опорные реакции балки
Определить координат центр тяжести
Ответ к задаче определить координат центр тяжести
Задача №20 Найти центр тяжести
Ответ к Задаче №20 Найти центр тяжести
Задача: Определить опорные реакции балки на двух опорах.
Проверить правильность их определения
Ответ к задаче: Определить опорные реакции балки на двух опорах. Проверить правильность их определения
Задача Определить центр тяжести
Ответ к задаче — Определить центр тяжести
Здравствуйте, помогите пожалуйста решить задачу по расчету прочности при расстяжении, сжатии
Ответ к задаче по расчету прочности при расстяжении, сжатии
Задача- Определить координат центра тяжести
Ответ к задаче Определить координат центра тяжести
Задача — Подобрать сечение стержня подвески поддерживающего брус
Ответ к задаче Подобрать сечение стержня подвески поддерживающего брус
Задача — Подобрать сечение стержня подвески поддерживающего брус
Ответ к задаче — Подобрать сечение стержня подвески поддерживающего брус
Задача: построить эпюры Qy и Mx для балки по данным в задании
Ответ построить эпюры Qy и Mx для балки по данным в задании
Задача: номер 1.
Определить реакции в опорах для балки
Ответ к задаче номер 1. Определить реакции в опорах для балки
Задача: построить эпюр Qy и Mx для балки, по данным в задании
Ответ к Задачи: построить эпюр Qy и Mx для балки, по данным в задании
Вариант № 3
Задание № 1 Определить изгибающий момент в точке С (справа)
Вариант № 2 Задание 1
Определить изгибающий момент в точке С . Построить эпюры поперечной силы и изгибающего момента
Вариант № 2 Задание 2
Ответ к Заданию № 2 рассчитать осевой момент инерции швеллера относительно оси Х
Задача № 3 Определить координаты центра тяжести
Ответ к задаче № 3
Задача 7
Ответ к задаче 7
Задача Проверить несущую способность балки
Ответ к задаче Проверить несущую способность балки
Задача — Момент силы относительно точки
Ответ к задаче — Момент силы относительно точки
Задача — Понятие о внецентренном растяжении ( сжатии)
Ответ к задаче — Понятие о внецентренном растяжении ( сжатии)
Задание
Ответ к заданию для Натальи Добринской
Задача: Определить реакцию опор двухопорной балки
Ответ
Задача
Ответ
Задача — столбец под номером 1
Ответ к задаче
Рисунок Д вариант чисел 1 Задача
Ответ к задаче
ПЕРЕХОДИ НА ДРУГУЮ СТРАНИЦУ САЙТА
ПО ССЫЛКЕ НИЖЕ
ОТВЕТЫ ПО ТЕХ-МЕХУ НА СЛЕДУЮЩЕЙ СТРАНИЦЕ
Как рассчитать площадь поперечного сечения
Обновлено 7 февраля 2020 г.
Кевин Бек
Вы можете столкнуться с ситуациями, когда у вас есть трехмерная твердотельная фигура и вам нужно вычислить площадь воображаемой плоскости, вставленной через фигуру и имеющей границы, определяемые границами твердого тела.
Например, если под вашим домом проходит цилиндрическая труба длиной 20 метров (м) и диаметром 0,15 м, вам может понадобиться узнать площадь поперечного сечения трубы.
Поперечные сечения могут быть перпендикулярны оси твердого тела, если таковые существуют. В случае сферы любая секущая плоскость, проходящая через сферу, независимо от ориентации, приведет к диску определенного размера.
Площадь поперечного сечения зависит от формы твердого тела, определяющей границы поперечного сечения, и угла между осью симметрии твердого тела (если она есть) и плоскостью, создающей поперечное сечение.
Площадь поперечного сечения прямоугольного тела
Объем любого прямоугольного тела, включая куб, равен площади его основания (длина, умноженная на ширину), умноженной на его высоту: V = l × w × h.
Следовательно, если поперечное сечение параллельно верхней или нижней части твердого тела, площадь поперечного сечения равна l × w. Если секущая плоскость параллельна одному из двух наборов сторон, площадь поперечного сечения вместо этого определяется как l × h или w × h.
Если поперечное сечение не перпендикулярно какой-либо оси симметрии, созданная форма может быть треугольником (если провести через угол тела) или даже шестиугольником.
Пример: Вычислить площадь поперечного сечения плоскости, перпендикулярной основанию куба объемом 27 м 3 .
Так как для куба l = w = h, длина любого ребра куба должна быть 3 м (поскольку 3
× 3
× 3 = 27). Таким образом, поперечное сечение описанного типа представляет собой квадрат со стороной 3 м, что дает площадь 9 м 2 .
Площадь поперечного сечения цилиндра
Цилиндр представляет собой твердое тело, образованное путем вытягивания окружности через пространство перпендикулярно ее диаметру.
Площадь круга находится по формуле πr 2 , где r — радиус. Поэтому имеет смысл, что объем цилиндра будет площадью одной из окружностей, образующих его основание.
Если поперечное сечение параллельно оси симметрии, то площадь поперечного сечения представляет собой просто круг площадью πr 2 . Если секущая плоскость вставляется под другим углом, создается эллипс. Для площади используется соответствующая формула: πab (где a — самое большое расстояние от центра эллипса до края, а b — самое короткое).
Пример: Какова площадь поперечного сечения трубы под вашим домом, описанной во введении?
Площадь поперечного сечения сферы
Любая теоретическая плоскость, проведенная через сферу, даст круг (подумайте об этом несколько минут). Если вы знаете диаметр или длину окружности, образуемой поперечным сечением, вы можете использовать соотношения C = 2πr и A = πr 2 для получения решения.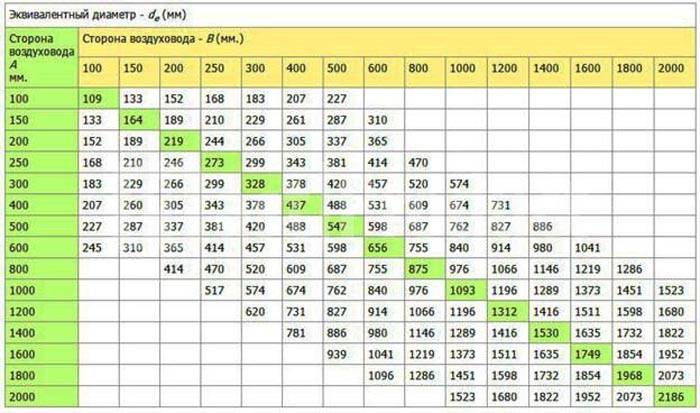
Пример 900:12: Самолет грубо вставлен в Землю очень близко к Северному полюсу, удаляя часть планеты в 10 м вокруг. Какова площадь поперечного сечения этого холодного куска Земли?
- Поскольку C = 2πr = 10 м, r = 10/2π = 1,59 м; A = πr 2 = π(1,59) 2 = 7,96 м 2 .
Эквивалент круглого воздуховода
Большинство существующих таблиц трения воздуховодов основаны на круглых воздуховодах. Это означает, что если вы работаете с прямоугольным воздуховодом или плоским овальным воздуховодом, вам нужно будет придумать эквивалентный размер круглого воздуховода, если вы используете какую-либо другую форму поперечного сечения, например, прямоугольный воздуховод или плоский овальный воздуховод. Условия Круглый эквивалент воздуховода и Эквивалентный диаметр звучат как одно и то же, но технически это два разных понятия с разными формулами для их расчета.
Формулы круглого эквивалента воздуховода опубликованы ASHRAE и используются для сравнения воздуховодов различной формы с точки зрения их пропускной способности по воздуху и позволяют использовать диаграмму трения воздуховодов, основанную на круглом воздуховоде, для воздуховодов других форм.
Формула эквивалентного диаметра опубликована AMCA и используется для определения эффективной длины воздуховода.
Вам может быть интересно, почему воздуховоды вообще бывают разной формы. Если нет ограничений по пространству, то для данного объема воздуха при заданном коэффициенте трения круглый воздуховод, вероятно, будет лучшим выбором по ряду причин, в том числе:
- последствия затрат.
- Меньший периметр, что означает снижение затрат на изоляцию и меньшую поверхность, через которую проходит теплопередача.
- Меньше низкочастотного шума прорыва; т.е. прямоугольные воздуховоды чаще грохочут.
Квадратные воздуховоды имеют аналогичные характеристики. Но по мере того, как соотношение сторон квадратного воздуховода начинает увеличиваться выше 1 (более широкий и тонкий воздуховод), тогда площадь поперечного сечения воздуховода, необходимая для подачи заданного расхода при заданном коэффициенте трения, будет увеличиваться, поскольку квадратные дюймы площади, содержащиеся на дюйм периметра начинает падать по сравнению с тем, что было бы для квадратного воздуховода или прямоугольного воздуховода.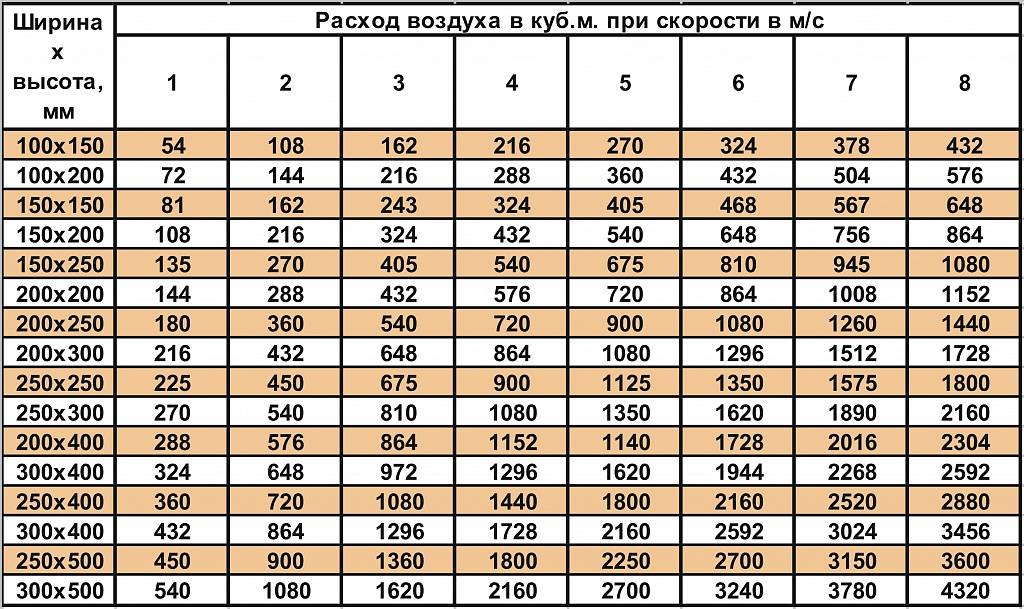
Интересным аспектом того факта, что воздуховод с большим удлинением требует большего поперечного сечения для подачи заданного расхода при заданном коэффициенте трения, является то, что скорость в воздуховодах с большим удлинением будет ниже, чем для квадратный или круглый воздуховод, по которому течет один и тот же поток с одинаковым коэффициентом трения. Поскольку падение давления в фитинге воздуховода является функцией скоростного давления, а скоростное давление является функцией квадрата скорости, из вышеизложенного следует, что неправильная конструкция фитинга будет более серьезной проблемой в круглом или квадратном воздуховоде по сравнению с той же конструкции фитинга, применяемой в воздуховоде с более высоким соотношением сторон, размер которого соответствует тому же расходу воздуха и коэффициенту трения.
В приведенной ниже таблице показаны некоторые пункты, сделанные выше.
По мере увеличения размеров воздуховода количество квадратных дюймов, охватываемых каждым дюймом периметра, также увеличивается.
Это означает, что при заданном коэффициенте трения большие каналы будут иметь гораздо более высокие скорости (и, следовательно, работать при гораздо более высоких скоростных давлениях), чем маленькие каналы. Это, в свою очередь, означает, что неправильная конструкция фитинга в большом воздуховоде может быть гораздо более серьезной проблемой, чем такая же неправильная конструкция фитинга в маленьком воздуховоде, потому что потери через фитинг являются функцией скоростного давления, которое, в свою очередь, является функция квадрата скорости.
В таблице ниже показано это явление.
ASHRAE определяет это как диаметр прямоугольного воздуховода, который имеет одинаковое сопротивление потоку при одинаковом расходе и длине. Это не то же самое, что термин AMCA Equivalent Duct, который будет обсуждаться в следующем разделе.
ASHRAE также публикует формулу для расчета круглого эквивалента плоскоовального воздуховода.
Стандарт AMCA 201 определяет термин «эквивалентный диаметр воздуховода» как диаметр круга, имеющего ту же площадь поперечного сечения, что и другая геометрическая форма.