Расчет конденсатора для трехфазного двигателя в однофазной сети онлайн: Онлайн расчет емкости конденсатора для электродвигателя

Калькулятор расчета емкости конденсатора — онлайн

f (кГц):
R (кОм):
UR (мВ):
UC (мВ):

Результаты расчета
C

Основной функцией каждого конденсатора является накопление электрического заряда и его одномоментная отдача в нужное время. Данные приборы используются во многих электрических схемах, существенно улучшая качество их работы. Для правильного выбора и оптимизации данных устройств используйте онлайн калькулятор расчета емкости конденсатора. Достаточно ввести в таблицу исходные данные, чтобы получить определенные результаты.

Как рассчитать емкость конденсатора

Расчеты, производимые с помощью онлайн калькулятора, позволяют вычислить емкость конденсатора в течение нескольких секунд. Кроме этого параметра, можно определить показатели заряда, мощности, тока, энергии и прочих качеств конденсатора, необходимых в конкретном устройстве.

Наиболее часто встречаются электролитические конденсаторы, применяемые в схеме асинхронного электродвигателя. Конструкции этих устройств могут быть полярными или неполярными. В первом случае отмечается более высокая емкость, поэтому перед подключением конденсатора к двигателю, необходимо в обязательном порядке выполнить расчеты. С помощью проводимых вычислений устанавливается необходимая емкость, соответствующая конкретному двигателю.

Особое значение придается дополнительным расчетам при эксплуатации трехфазных электродвигателей. В обычном режиме конденсатор функционирует нормально, однако при включении в однофазную сеть, его емкость заметно снижается. Это приводит к увеличению частоты вращения вала.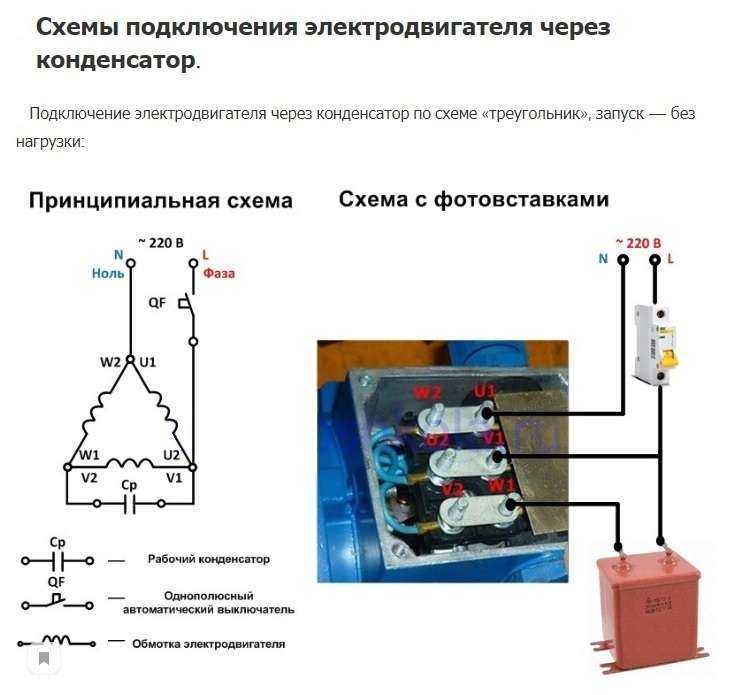 Предварительные расчеты и правильное подключение позволяют избежать подобных ситуаций.

При запуске асинхронного двигателя, работающего от напряжения 220 вольт, требуется конденсатор с высокой емкостью. В связи с этим, невозможно обойтись без проведения расчетов с помощью онлайн калькулятора. Проведение расчетов полностью зависит от способа соединения обмоток электродвигателя. Данное соединение может быть выполнено двумя способами – звездой и треугольником. В первом случае применяется формула Ср=2800хI/U, а для второго случая используется немного измененная формула Ср=4800хI/U.

Следует учитывать, что в цепочке соединенных конденсаторов емкость пускового устройства должна быть примерно в три раза выше, чем в рабочем приборе. Для расчета применяется формула Сп=2.5хСр, в которой Сп и Ср являются соответственно пусковым и рабочим конденсатором.

Методика расчета заряда конденсатора

В начальной стадии заряд любого прибора имеет нулевое значение. После подключения к гальваническому элементу или другому источнику постоянного тока происходит зарядка конденсатора.

В таблицу калькулятора вводятся такие данные, как значение ЭДС источника тока в вольтах, сопротивление, измеряемое в омах, емкость прибора в микрофарадах и время зарядки в миллисекундах. В результате вычислений появляются точные данные, характеризующие заряд конкретного конденсатора и определяющие его оптимальное использование в той или иной схеме.

Расчет конденсатора фазового сдвига — www.itieffe.com

Cспиртовой конденсатор фазового сдвига

Cспиртовой конденсатор фазового сдвига

Работа трехфазного асинхронного двигателя происходит из-за подачи питания на трехфазный ток, которые не совпадают по фазе между ними на 120 °.

Возможно питание одного и того же двигателя однофазным током nи случаи, в которых требуемая мощность не составляет 100% (и то же самое не превышает определенные мощности) через конденсатор фазового сдвига

Эффективность не будет высокой, поскольку полученный фазовый сдвиг не является оптимальным.

Однако он может применяться для различных целей: электронасосы, центробежные и винтовые вентиляторы, дрели и для всех тех машин с ограниченной мощностью и не требующих высоких пусковых токов.

В большинстве случаев используется соединение треугольником, подходящее для трехфазного двигателя 220–380 В, питаемого от однофазного 220 В.

На следующем рисунке показаны соединения для трехфазных асинхронных двигателей с однофазным питанием со звездой и треугольником, а также с вращением по и против часовой стрелки.

треугольникСтелла

Конденсатор производит фазовый сдвиг, необходимый для создания вращающегося магнитного поля внутри двигателя.

Величина фазового сдвига является результатом задействованной емкости и тока, по этой причине фазовый сдвиг никогда не может быть оптимальным, он меняется в зависимости от нагрузки и всегда будет компромиссом.

Двигатель с таким питанием никогда не сможет обеспечить номинальную мощность, при рассчитанном здесь значении мощность снижается до 60-70% и является компромиссом для работы с ограниченными и средними нагрузками.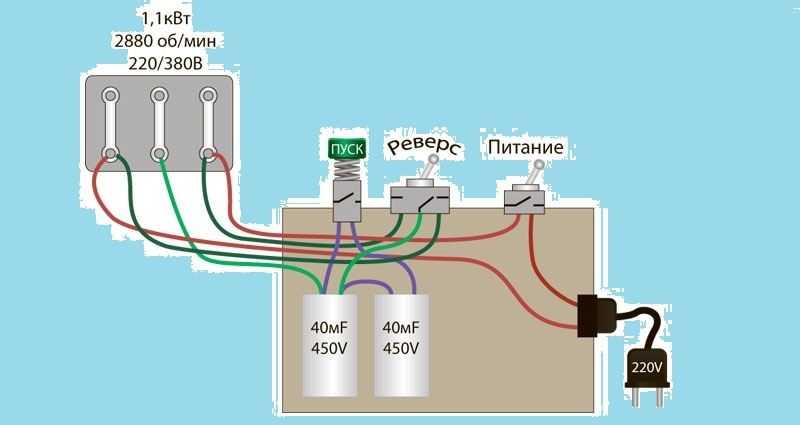

Самый высокий пусковой момент для однофазного двигателя достигается, когда задержка, которую мы получаем с нашим конденсатором, составляет 90 °.

В случаях, когда нагрузка всегда высока, можно увеличить мощность для получения большей мощности, но будьте осторожны, в этом случае он не должен работать без нагрузки или с низкими нагрузками, вы рискуете сжечь двигатель.

Неверно думать, что с большим конденсатором он получает больше мощности, даже сбой может возникнуть у пользователя.

Наибольшее ухудшение этого типа соединения происходит в фазе пуска, доступный крутящий момент составляет 30-40% от крутящего момента, достигаемого при обычном питании двигателя.

Предупреждения

Помните, что в этом конкретном приложении конденсатор подвержен сильным токам и неоднократным изменениям полярности, если он не подходит для выполняемой работы, он может взорваться.

Используйте только неполяризованные конденсаторы с максимальным рабочим напряжением на 15-20% выше напряжения питания двигателя и рассчитанные на переменный ток.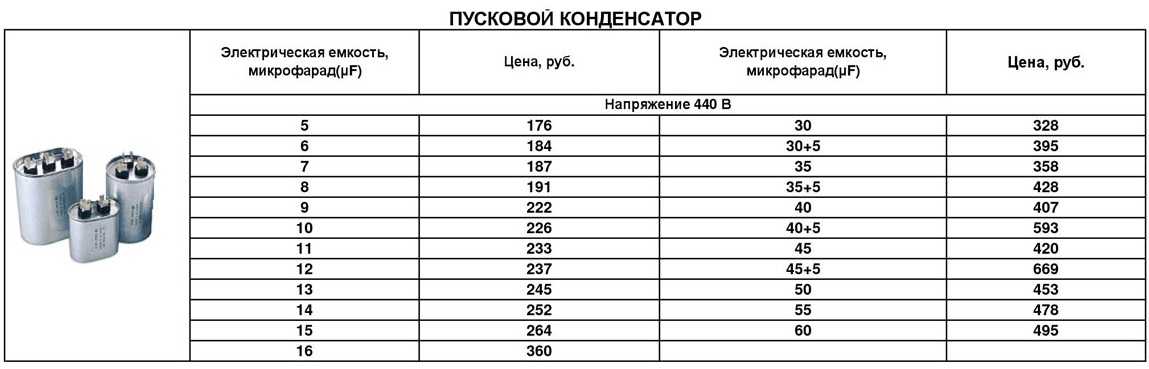

Другие бесплатные программы, предлагаемые itieffe ▼

• Закон Ома — калькулятор
• Выбор электрических кабелей
  
• Степени защиты IP
• Расчет мощности и тока двигателя
• Кабели электропитания
• Размеры электрических кабелей — калькулятор
• Коэффициент мощности (cos Ø)
• Скорость электродвигателей — Поляки
• Кабели электропитания
• Максимальная длина электрического кабеля

itieffe.com >>> Расчет конденсатора фазового сдвига ▼

3-фазное питание: объяснение треугольника и звезды

Электричество используется для питания множества устройств, разработанных для удобства и необходимости людей и процессов по всему миру. Трехфазное питание играет ключевую роль при проектировании электрических систем, а трехфазные фильтры электромагнитных помех являются важной частью электрических устройств на различных рынках, в первую очередь в тяжелых промышленных условиях. Большинству устройств промышленного назначения требуется высокая мощность для подачи достаточного количества электроэнергии для поддержки больших двигателей, систем отопления, инверторов, выпрямителей, источников питания и индукционных цепей. В связи с этим мощное оборудование обычно проектируется для трехфазного или многофазного питания переменного тока, в котором общая потребляемая мощность делится между многими фазами, оптимизируя энергосистему (генерация и распределение) и конструкцию оборудования.

В трехфазной системе есть три проводника, по которым проходит переменный ток. Они называются фазами и обычно обозначаются как A, B и C. Каждая фаза настроена на одну и ту же частоту и амплитуду напряжения, но сдвинута по фазе на 120°, что обеспечивает постоянную передачу мощности во время электрических циклов.

Конфигурации с трехфазным питанием особенно важны, поскольку они могут поддерживать в три раза больше энергии, используя всего в 1,5–2 раза больше проводов, чем однофазные конфигурации питания. Это может помочь снизить стоимость и количество материалов, необходимых для проектирования энергосистемы. Это также может упростить конструкцию двигателя за счет устранения необходимости в пусковых конденсаторах.

Однако при преобразовании большой мощности (инвертировании, выпрямлении) возникает чрезмерно высокочастотный шум (ЭМП), который обычно является высшими гармониками различных частот переключения.

По этой причине 3-фазные фильтры электромагнитных помех становятся особенно важными в 3-фазных приложениях, поскольку они уменьшают количество электромагнитных помех, предотвращают нарушения работы оборудования и помогают компаниям соблюдать правила ЭМС.

В чем разница между системами Delta и WYE?

Трехфазные системы могут быть сконфигурированы двумя различными способами для поддержания одинаковой нагрузки; они известны как конфигурации Delta и WYE. Названия «треугольник» и «звезда» являются конкретными индикаторами формы, которую провода напоминают после соединения друг с другом. «Дельта» происходит от греческого символа «Δ», а «звезда» напоминает букву «Y» и также известна как схема «звезда». Обе конфигурации, треугольник и звезда, могут подавать питание по трем проводам, но принципиальные различия между ними основаны на количестве проводов, доступных в каждой конфигурации, и протекании тока. Конфигурация WYE приобрела популярность в последние годы, потому что она имеет нейтральный провод, который позволяет подключать как линию к нейтрали (одна фаза), так и линия к линии (2/3 фазы).

Что такое трехфазные сетевые фильтры?

Трехфазные фильтры электромагнитных помех разработаны в соответствии со строгими требованиями норм ЭМС для промышленных применений. Правила определяют максимально допустимые уровни шума (в дБ) на линиях электропередач. Общие требования к конструкции трехфазного фильтра электромагнитных помех включают входные токи, линейное напряжение, ограничения по размеру и требуемые вносимые потери. В дополнение к этому, конфигурация 3-фазного фильтра электромагнитных помех играет важную роль в конструкции.

Трехфазный фильтр «треугольник» и сетевой фильтр «звезда» Объяснение

Трехфазный фильтр электромагнитных помех

Трехфазный фильтр электромагнитных помех предназначен для уменьшения электромагнитных помех в устройствах, подключенных к трехфазному питанию треугольником. Конфигурация Delta содержит четыре провода; три горячих проводника и один заземляющий проводник. Фазные нагрузки (например, обмотки двигателя) соединяются друг с другом в форме треугольника, где соединение осуществляется от одного конца обмотки к пусковому концу другого, образуя замкнутую цепь.

Эта конфигурация питания не имеет нейтрального провода, но может питаться от трехфазной сети, соединенной звездой, если нейтральная линия отсутствует/заземлена. Система «треугольник» используется для передачи электроэнергии из-за более низкой стоимости из-за отсутствия нулевого кабеля.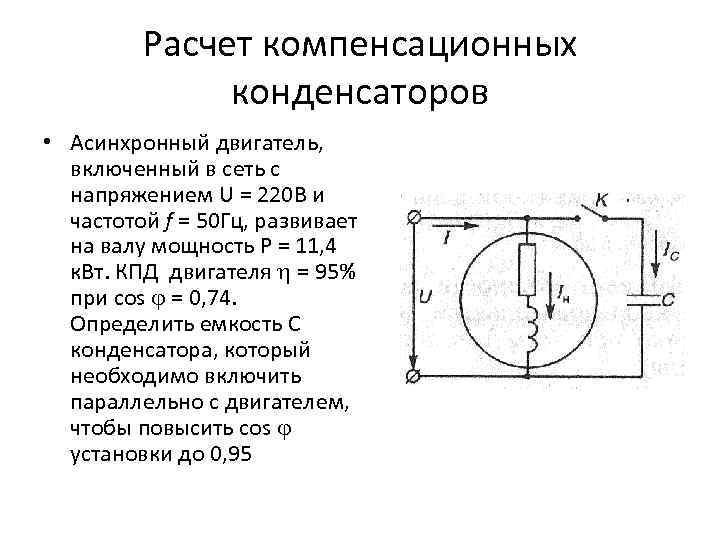 Он также используется в приложениях, требующих высокого пускового момента.

Из-за отсутствия нейтрального провода конденсаторы, используемые в 3-фазных фильтрах электромагнитных помех Delta, должны быть рассчитаны на линейное (фазовое) напряжение, что может увеличить размер, вес и стоимость. Однако отсутствие нейтрального провода обеспечивает более высокие номинальные токи, чем звезда, и лучшую производительность при том же заданном кубическом объеме.

 

Проектирование и трехфазный фильтр электромагнитных помех Delta

1. Определите максимальную мощность, требуемую нагрузкой.
2. Разделите максимальную мощность, требуемую нагрузкой, на 3, чтобы получить мощность на фазу.
3. Разделите ответ на междуфазное напряжение.
4. Умножьте предыдущий ответ на квадратный корень из 3.

Каковы преимущества дельта-конфигураций?

• Конфигурации треугольника обычно могут быть разработаны для работы с более высоким током и более эффективны.
• Защита для дельта-конфигураций может быть простой.
Конфигурации
• Delta обычно настраиваются для тяжелых условий эксплуатации и предпочтительнее для производства и передачи электроэнергии.

 

3-фазный фильтр электромагнитных помех по схеме «звезда»

Фильтры электромагнитных помех по схеме «звезда» предназначены для фильтрации типовых импульсных преобразователей мощности и других устройств, требующих подключения нейтрали. Эта конфигурация состоит из пяти проводов; три горячих проводника, нейтраль и земля. В конфигурации «звезда» фазные нагрузки подключаются к одной (нейтральной) точке, где подключается нейтральный провод.

Когда нагрузки конфигурации «звезда» полностью сбалансированы, ток через нейтральный провод не течет. Когда нагрузки несимметричны, по нейтральному проводу течет ток. Эта конфигурация позволяет использовать конденсаторы более низкого напряжения (120 В переменного тока в системе 208 В переменного тока и 277 В переменного тока в системе 480 В переменного тока) в фильтре, что может привести к экономии стоимости, веса и объема.

Во многих случаях нейтральный провод может оставаться незаземленным. Однако, как упоминалось ранее, конфигурация «звезда» обеспечивает гибкость подключения нагрузок в цепи либо фаза-нейтраль, либо фаза-линия. В отличие от Delta, эта конфигурация может использоваться как четырехпроводная или пятипроводная схема. Конфигурации WYE обычно используются в сетях распределения электроэнергии. Это в первую очередь требуется в приложениях, которые требуют меньшего пускового тока и перемещаются на большие расстояния.

Проектирование и трехфазный фильтр электромагнитных помех по схеме «звезда»

1. Определите максимальную мощность, необходимую для нагрузки.
2. Разделите максимальную мощность, требуемую нагрузкой, на 3, чтобы получить мощность на фазу.
3. Разделите ответ на напряжение фаза-нейтраль/земля.

Каковы преимущества конфигураций WYE?

• Предпочтительно для распределения электроэнергии, так как может поддерживать однофазную (фаза-нейтраль), 2-фазную (фаза-фаза) и трехфазную нагрузку.
• Звезда обычно заземлена, что делает ее идеальной для несбалансированных нагрузок.
• Для поддержки того же напряжения требуется меньшая изоляция.

Стоимость трехфазных сетевых фильтров Delta против WYE

Часто возникает вопрос, какие трехфазные фильтры электромагнитных помех Delta или WYE более экономичны. Конфигурация трехфазного дельта-фильтра электромагнитных помех технически может быть более рентабельной, чем конфигурация WYE, поскольку для нее требуются только трехжильные кабели вместо четырех, что снижает стоимость материалов для сборки блоков. Тем не менее, некоторые из этих затрат и выгод могут быть компенсированы потребностью в компонентах, рассчитанных на высокое напряжение.

Трехфазный фильтр электромагнитных помех Astrodyne TDI в конфигурациях «треугольник» и «звезда»

Astrodyne TDI предлагает трехфазные фильтры электромагнитных помех в конфигурациях «треугольник» и «звезда», которые помогают уменьшить электромагнитные помехи в различных приложениях и обеспечивают соответствие международным стандартам излучения. Наши трехфазные фильтры электромагнитных помех рассчитаны на напряжение от 480/520 В переменного тока до 600 В переменного тока с номинальным током до 2500 А. Сетевые фильтры предлагаются в одно-, двух- и многоступенчатом исполнениях с более высокими значениями тока и напряжения по запросу.

Обладая обширным ассортиментом фильтров и широкими возможностями проектирования, наша команда инженеров может гарантировать, что найдет наиболее эффективное решение для трехфазного фильтра электромагнитных помех, отвечающее любым спецификациям и самым сложным приложениям.

Просмотрите наш выбор трехфазных фильтров электромагнитных помех или свяжитесь с нашей командой, чтобы узнать больше о продукте, который поможет удовлетворить ваши требования.

Механические характеристики трехфазных асинхронных двигателей с однофазным питанием.

УДК 621.313.33

Введение. Асинхронные двигатели (АД) в основном выпускаются с трехфазные обмотки, питаемые симметричной трехфазной системой напряжения. Однако на практике может потребоваться переход на однофазный сети [1], в которых используются конденсаторы, создающие сдвиг фазного тока в катушке и магнитном поле двигатель становится пульсирующим и вращающимся, вызывая электромагнитный момент. Также разработаны и широко используются конденсаторные электродвигатели, которые предназначены для работы от однофазной сети [5]. И в первом, и во втором случае возникает проблема расчет их пусковых характеристик и конденсаторов выбор емкости.

В технической литературе, поскольку метод расчета для различных номиналы конденсаторов известны [1, 2], но эти методы не достаточной точностью, поскольку не учитываются должным образом такие факторы, как как асимметрия мощности магнитного насыщения и тока смещения. Проблемы анализа режимов работы АД методом математического моделирования необходимо решить две задачи: выбор математической модели двигатель и метод расчета. Эти проблемы взаимосвязаны, поскольку использование упрощенной математической модели АД не может адекватно учитывать факторы, определяющие точность расчетов, а использование более сложных моделей требует использования соответствующий математический аппарат.

Цель работы — разработка методики и алгоритма расчет механических характеристик асинхронных двигателей, питаются от однофазной сети.

Система уравнений. Трехфазный АД с конденсаторами в одном фаза по определению перекошена со стороны статора, а значит для анализа электромагнитных процессов в их наиболее адекватном и оптимальной системой координат является трехфазная, а не физическая, т. н. ингибируется [4]. В этой системе контуры статора не преобразованы, что позволяет адекватно описывать процессы в них, и трехфазная обмотка ротора заменена равноценной стационарной фазой, ось которого совпадает с осью обмотки статора.

Система уравнений, описывающая электромагнитные процессы в АД, трехфазная обмотка статора питается от однофазной сети показанное на рис. 1, имеет вид [4]

[МАТЕМАТИЧЕСКОЕ ВЫРАЖЕНИЕ НЕ ВОСПРОИЗВОДИМО В ASCII] (1)

, где [u.sub.BC] = [квадратный корень из 3][U.sub.m] sin([[omega]. sub.0]t — [pi]/2) – линейное напряжение питания; [U.sub.m], [[omega].sub.0] являются амплитуда фазного напряжения и угловая частота; [альфа] = [[омега].sub.0](1 — s)/[квадратный корень из (3)]; s – скольжение; [[psi].sub.[xi]], [i.sub.[xi]], [r.sub.[xi]] ([xi] = A, B, C, a, b, c) – потокосцепления, токи и активные опоры цепей; uk — напряжение на конденсаторе емкостью С.

Методика и алгоритм расчета. Запишем (1) через единицу векторное уравнение m = 7-го порядка в виде

[МАТЕМАТИЧЕСКОЕ ВЫРАЖЕНИЕ, НЕ ВОСПРОИЗВОДИМОЕ В ASCII], (2)

где

[МАТЕМАТИЧЕСКОЕ ВЫРАЖЕНИЕ НЕ ВОСПРОИЗВОДИМО В ASCII].

Система дифференциальных уравнений (2) в форме Коши выглядит

[МАТЕМАТИЧЕСКОЕ ВЫРАЖЕНИЕ НЕ ВОСПРОИЗВОДИМО В ASCII]. (3)

Поскольку вектор [??](t) = [??](t + T) является периодической функцией времени в стационарном режиме (при s = const) решение системы уравнение (3) представляет собой Т-периодические зависимости вектора [??](t) = [??](t + Т) компоненты.

Определение периодических функциональных взаимосвязей компоненты вектора [??] путем вычисления перехода к институционализация неприемлема по многим причинам. Такая проблема может наиболее эффективно решать во вневременной области путем решения границы задача, разработанная на основе общей теории нелинейных метод проектирования колебаний, основанный на теоретическом приближении координаты состояния сплайнов третьего порядка [3]. Формирование границы задача выполняется на сетке из n узловых точек периода T. результатом аппроксимации одного дифференциального уравнения системы (3) является система алгебраических уравнений n-го порядка

[МАТЕМАТИЧЕСКОЕ ВЫРАЖЕНИЕ, НЕ ВОСПРОИЗВОДИМОЕ В ASCII], (4)

где H — матрица перехода от непрерывных координат к их узловые значения, элементы которых определяются только узлами сетки [3]; [МАТЕМАТИЧЕСКОЕ ВЫРАЖЕНИЕ НЕ ВОСПРОИЗВОДИМО В ASCII], и для система дифференциальных уравнений (2) — m векторных уравнений в виде (4)

[МАТЕМАТИЧЕСКОЕ ВЫРАЖЕНИЕ НЕ ВОСПРОИЗВОДИМО В ASCII], (5)

где [МАТЕМАТИЧЕСКОЕ ВЫРАЖЕНИЕ НЕ ВОСПРОИЗВОДИМО В ASCII];

[МАТЕМАТИЧЕСКОЕ ВЫРАЖЕНИЕ НЕ ВОСПРОИЗВОДИМО В ASCII].

Нелинейная система (5) алгебраических уравнений mn-го порядка представляет собой дискретное отражение нелинейной системы дифференциальных уравнений (2) порядка m и i приближается к периоду T. Его решением является вектор [??] компонентами которого являются значения токов ветвей и напряжения на конденсатор в сети. С его помощью можно рассчитать не только устойчивые но также исследовать влияние изменения работы двигателя на любой должность, которая является частью системы. Для расчета установившегося режима данный слайд метод продолжения по параметру. Для этой системы (5) вводим параметр e путем умножения вектора приложенного напряжения к е и дифференцировать ее на нем. В результате получаем дифференциальное уравнение (ДУ)

[МАТЕМАТИЧЕСКОЕ ВЫРАЖЕНИЕ НЕ ВОСПРОИЗВОДИМО В ASCII], (6)

где [МАТЕМАТИЧЕСКОЕ ВЫРАЖЕНИЕ НЕ ВОСПРОИЗВОДИМО В ASCII] Блочные элементы матрицы Якоби, элементы которых [МАТЕМАТИЧЕСКОЕ ВЫРАЖЕНИЕ НЕ ВОСПРОИЗВОДИМО В ASCII] определяются значениями параметров ИМ в j-й узел.

[МАТЕМАТИЧЕСКОЕ ВЫРАЖЕНИЕ НЕ ВОСПРОИЗВОДИМО В ASCII].

Интегрирующая система ДР (6) по [эпсилон] от [эпсилон] = 0 до [эпсилон] = 1 находим значения вектора [??] при заданном напряжении, которое можно уточнить методом Ньютона.

Для исследования влияния на режим работы ИМ любого изменения координаты, необходимые с учетом неизменного вектора приложенного напряжения, мы продифференцируем систему (5) по этой координате как параметру. В частности, при расчете механических характеристик получаем система ДЭ

[МАТЕМАТИЧЕСКОЕ ВЫРАЖЕНИЕ НЕ ВОСПРОИЗВОДИМО В ASCII], (7)

интегрируя которые получаем многомерную характеристику. Таким образом, матрица Якоби, такая как в (6), и вектор правых частей состоят из n векторы в виде

[МАТЕМАТИЧЕСКОЕ ВЫРАЖЕНИЕ НЕ ВОСПРОИЗВОДИМО В ASCII],

где [частная производная]B/[частная производная]s равна матрица B, в которой [альфа] = -[[омега].sub.0]/[квадратный корень из (3)].

Решена задача расчета механических характеристик в два этапа: на первом рассчитаем установившийся режим при скольжении s = 1. 0, а на втором — зависимости координат как функции проскальзывание от s = 1,0 до заданного значения, а на его основе — механическое характеристика [M.sub.e] = [M.sub.e](s). Электромагнитный момент ИМ рассчитывается по формуле [4]

[M.sub.e] = p/[квадратный корень из (3)] [I.sub.[mu]] (([i.sub.[mu]B] — [i.sub.[mu]C]) [i.sub.A] + ([i.sub.[mu]C] — [i.sub.[mu]A])[i.sub.B] + ([i.sub.[mu]A] — [i.sub.[mu]B])[i.sub.C]).

Для определения матричных элементов [L.sub.j] дифференцированного индуктивности характеристическая намагниченность основного магнитного пути и рассеяние в зависимости от рассеяния потока статора (s) и ротора (r) используются соответствующие токи [4]

[[psi].sub.[mu]] = [[psi].sub.[mu]] ([i.sub.[mu]]), [[psi].sub.[sigma]s] ([i.sub.s]), [[psi].sub.[sigma]r] = [[psi].sub.[sigma]r] ([i.sub.r]),

где [i.sub.s], [i.sub.r] — модули векторов, представляющих эти токи.

Для учета тока смещения в стержнях ротора каждый из них вместе с короткозамкнутыми кольцами, разделенными по высоте на k слои. То есть считается, что в роторе имеется k короткозамкнутых обмотки с соответствующими размерами и каждая заменена на трехфазный. В этих условиях система уравнений (1) вместо трех уравнений для ротора мы должны написать 3k уравнений вида

[МАТЕМАТИЧЕСКОЕ ВЫРАЖЕНИЕ НЕ ВОСПРОИЗВОДИМО В ASCII].

Увеличение количества уравнений не влияет на расчет алгоритм и мало влияет на объем вычислений, так как плохо заполненная матрица Якоби, позволяющая решить систему уравнений с помощью алгоритм, учитывающий его структуру.

Примеры результатов математического моделирования представлены на рис. 2, 3.

Заключение.

Разработанный метод расчета статических механических свойств трехфазных АД с короткозамкнутым ротором, которые питаются от однофазной сети позволяет исследовать влияние конденсаторов емкость на процесс, чтобы выбрать начало и его значение, которое обеспечивает необходимый пусковой момент. В основе алгоритма лежит математическая модель АД, учитывающая магнитное насыщение и смещение тока в стержнях ротора, а дифференциальный метод расчета статических характеристик, основанный на решении краевая задача для системы дифференциальных уравнений электрических баланс.

doi: 10.20998/2074-272X.2016.3.03

ССЫЛКИ

[1.] Беспалов В.Я., Мощинский Ю.А., Петров А.П. Динамика индикаторы трехфазных асинхронных двигателей, подключенных к однофазным поставлять. Электротехника—Электротехника, 2000, №1. 1, стр. 13-19. (Рус).

[2.] Бешта А.С., Семин А.А. Оценка параметров эквивалентная схема асинхронного двигателя при несимметричном питании к статору. Электромеханические и энергохозяйства системы—Электромеханические и энергосберегающие системы, 2014, т. 1, с. 2, с. 10-16. (Рус).

[3.] Маляр В.С., Маляр А.В. Математическое моделирование периодических режимы электротехнических устройств. Электронное моделирование—Electronic Моделирование, 2005, вып. 27, нет. 3, стр. 39-53. (Рус).

[4.] Фыльц Р.В. Математические основы теории Электромеханических преобразователей. теория электромеханических преобразователей. Киев, издательство «Наукова думка», 1979. 208 с. (Рус).

[5.] Шуруб Ю.В. Математическая модель асинхронного конденсатора двигатель с тиристорным управлением.