Как рассчитать емкость гасящего конденсатора простого блока питания. . Обзоры товаров из Китая.
Блок питания с гасящим конденсатором представляет собой простейший вариант запитать какое нибудь маломощное устройство.При всей своей простоте он имеет и два минуса:
1. Он гальванически связан с сетью! потому такие БП используются там, где нет вероятности прикосновения к контактам.
2. Такой Бп имеет не очень большой выходной ток. При увеличении выходного тока надо увеличивать емкость гасящего конденсатора и его габариты становятся существенными.
Внимание, будьте очень аккуратны, не прикасайтесь к контактам этого БП когда он включен.
Простейшая схема данного БП выглядит так:
Как можно увидеть из схемы, последовательно с сетью стоит конденсатор. Он то и является балластом,, на котором гасится часть напряжения.
Конденсатор не пропускает постоянный ток, но так как в сети переменный и конденсатор в итоге постоянно перезаряжется, то и получается, что в таком случае ток на выходе есть.
Причем сила тока напрямую зависит от емкости конденсатора.
Собственно потому для расчета емкости конденсатора необходимо знать как минимум выходной ток нашего будущего БП, причем надо учесть и потребление стабилизатора, обычно это несколько мА.
И так. Есть две формулы, сложная и простая.
Сложная — подходит для расчета при произвольном выходном напряжении.
Простая — подходит в ситуациях, когда выходное напряжение не более 10% от входного.
I — выходной ток нашего БП
Uвх — напряжение сети, например 220 Вольт
Uвых — напряжение на выходе БП (или до стабилизаторе если такой есть), например 12 Вольт.
С — собственно искомая емкость.
Например я хочу сделать БП с выходным током до 150мА. Пример схемы приведен выше, вариант применения — радиопульт с питанием 5 Вольт + реле на 12 Вольт.
Подставляем наши 0.15 Ампера и получаем емкость 2.18мкФ, можно взять ближайший номинал из стандартных — 2,2мкФ, ну или «по импортному» — 225.
Все как бы вроде хорошо, схема простая, но есть несколько минусов, которые надо исключить:
Бросок тока при включении может сжечь диодный мост.2. При выходе из строя конденсатора может быть КЗ
3. Если оставить как есть, то вполне можно получить разряд от входного конденсатора, так как на нем может долго присутствовать напряжение даже после отключения БП от сети.
4. При снятии нагрузки напряжение на конденсаторе до стабилизатора поднимется до довольно большого значения.
Решения:
1. Резистор R1 последовательно с конденсатором
2. Предохранитель 0.5 Ампера.
3. Резистор R2 параллельно конденсатору.
4. Супрессор на 12 Вольт параллельно конденсатору после диодного моста. Я не рекомендую здесь использовать стабилитроны, супрессоры рассчитаны на большую мощность рассеивания и схема будет работать надежнее.
На схеме красным цветом я выделил новые компоненты, синим — небольшое дополнение в виде светодиода.
Но гасящие конденсаторы используют часто и в дешевых светодиодных лампах. Это плохо, так как у таких ламп меньше надежность и часто высокие пульсации света.
Ниже упрощенный вариант схемы такой лампы.
Попробуем рассчитать емкость для такого применения, но так как напряжение на выходе будет явно больше чем 1/10 от входного, то применим первую формулу.
В качестве выходного напряжения я заложил 48 Вольт, 16 светодиодов по 3 Вольта на каждом. Конечно это все условно, но близко к реальности.
Ток — 20мА, типичный максимальный ток для большинства индикаторных светодиодов.
У меня вышло, что необходим конденсатор емкостью 0.298 мкФ. Ближайший из распространенных номиналов — 0.27 или 0.33мкФ. Первый встречается гораздо реже, а второй уже будет давать превышение тока, потому можно составить конденсатор из двух параллельных, например по 0.15мкФ. При параллельном включении емкость складывается.
С емкостью разобрались, осталось еще пара моментов:
1. Напряжение конденсатора
2. Тип конденсатора.
С напряжением все просто, можно применить конденсатор на 400 Вольт, но надежнее на 630, хоть они и имеют больше размер.
С типом чуть сложнее. Для такого применения лучше использовать конденсаторы, которые изначально предназначены для такого использования, например К73-17, CL21, X2
На фото конденсатор CL21
А это более надежный вариант, не смотрите что на нем указано 280 Вольт, у него это значение переменного действующего напряжения и он будет работать надежнее, чем К73-17 или CL21.
Такие конденсаторы могут выглядеть и так
А вот теперь можно еще раз внимательно посмотреть, что надо для того, чтобы собрать такой «простой» блок питания и решить, нужен ли он.
Как пример таких блоков питания я могу дать ссылку на подробный обзор четырех вариантов, с тестами, схемами и осмотров.
Но можно поступить еще лучше.
Сейчас получили распространение монолитные блоки питания. По сути кубик, в котором находится миниатюрный БП
Например HLK-PM01 производства Hi-link, стоимостью около двух долларов за штуку.
Или их китайский аналог TSP-05 производства Tenstar robot. Они немного дешевле, 1.93 доллара за штуку.
Практика показала, что качество у них сопоставимое.
Как я писал выше, они представляют из себя импульсный Бп в модульном исполнении. БП в пластмассовом корпусе залитый эпоксидной смолой.
Внутренности поближе, на фото вариант от Hi-link
На этом вроде все. Надеюсь, что статья была полезна, постараюсь и в будущем находить интересные темы. Также интересны пожелания, что хотелось бы видеть в рубрике — Начинающим.
Эту страницу нашли, когда искали:
емкость гасящего конденсатора на ток 0,5 а, как расчитать необходимый конденсатор в ибп, ограничение мошности емкостью конденсатора, конденсатор для ограниченя напряжения, напряжение и емкость конденсатора для зарядного 24в, делитель напряжения после моста 220вольт, какую емкость пленочного конденсатора взять для блока питания, как выбрать конденсаторы для блока питания, подбор электролитического конденсатора в блок питания, мощный конденсаторный блок питания, рассчитать гасящий конденсатор для понижения напряжения, какая на выходе стабилизированного блока питания должна быть емкость конденсатора, конвертер гасящего конденсатора на 220в, как расчитать какой емкости ставить конденсатор в схема усилительного каскада, как подобрать конденсатор в блок питания 12 вольт, расчет входного конденсатора безтрансформаторного бп, какие ставить конденсаторы в бп чтобы увеличить мощность, схема включения x2 конденсатора, как подобрать конденсатор для блока питания 36 вольт, расчет емкости конденсатора qx/Uвых, конденсатор гасящий калькулятор, сколько вольт вы найдете на основном конденсаторе прибора на 220 вольт, как рассчитать выходное напряжение через конденсатор, конденсатор 0.
| Расчет величины поверхности теплообмена | |
|---|---|
| Скорость воды, м/с (для МНЖ5-1 ― не более 2 м/с) | 2 |
| Температура насыщения пара \(t_{н},\;^\circ{С}\) | 27,77 |
| Удельная паровая нагрузка (первое приближение) \(d_к\), г/(м2*с) | 11,00 |
| Фактор паровой нагрузки для номинального расхода пара | 1 |
| Фактор скорости \(Ф_w\) | 1,0012 |
| Фактор температуры \(Ф_t\) | 0,79 |
| Фактор числа ходов \(Ф_z\) | 1 |
| Коэффициент теплопередачи, Вт/(м2*К) | 2580 |
| Температура воды на выходе конденсатора, \(^\circ{С}\) | 21,42 |
| Среднелогарифмическая разность температур, \(^\circ{С}\) | 10,35 |
| Поверхность теплообмена, м2 | 14274 |
| Расчетная удельная паровая нагрузка, \(d_к*\), г/(м2*с) | 10,79 |
| Точность расчета удельной паровой нагрузки, % | 0,29 |
| Расчет величины поверхности теплообмена | |
|---|---|
| Удельная паровая нагрузка (второе приближение) \(d_к\), г/(м2*с) | 10,79 |
| Фактор паровой нагрузки \(Ф_d\) | 1 |
| Фактор скорости \(Ф_w\) | 1,0012 |
| Фактор температуры \(Ф_t\) | 0,79 |
| Фактор числа ходов \(Ф_z\) | 1 |
| Коэффициент теплопередачи, Вт/(м2*К) | 2580 |
| Температура воды на выходе конденсатора, \(^\circ{С}\) | 21,42 |
| Среднелогарифмическая разность температур, \(^\circ{С}\) | 10,35 |
| Поверхность теплообмена, м2 | 14276 |
| Расчетная удельная паровая нагрузка, \(d_к*\), г/(м2*с) | 10,97 |
| Точность расчета удельной паровой нагрузки, % | 0,001 |
| Количество трубок конденсатора, шт | 23267 |
| Полезная длина трубок, м | 7,813 |
| Условный диаметр трубной доски, м | 6,741 |
Простые формулы конденсатора для накопления энергии
У вас есть конденсатор или вам нужно выбрать его, вы хотите рассчитать кое-что о нем с точки зрения использования его для хранения/передачи энергии (в отличие от фильтрации), вы хотели бы просто знать немного больше, чем онлайн-калькулятор, но не намного больше, потому что математика заставляет ваш мозг болеть.
Эта страница для вас.
ln() (Natural Log) часто появляется в уравнениях, натуральный log является обратным преобразованию e в степень чего-либо (то есть ln(e x ) = x ), в электронных таблицах это функция «ln()», в коде (например, C/C++ [Arduino!]) это обычно функция «log()».
Все формулы предполагают «идеальный» конденсатор, не учитываются ESR или другие неидеальные характеристики. Этого достаточно, чтобы вы оказались на стадионе.
Вы можете изменить поля в каждом разделе, чтобы сделать свой собственный расчет.
Помните, что напряжение питания для зарядки конденсатора не должно превышать максимальное номинальное напряжение конденсатора (в общих чертах).
У меня есть неизвестный конденсатор, известный резистор и секундомер, рассчитайте емкость.
C = (0 — Секунды) / R / ln(1-(VCharged/VSupply))
Где Секунды — количество секунд, за которые взимается плата; R — сопротивление в Омах; VCharged — напряжение конденсатора в секундах; VSupply – напряжение питания.
Вам не нужно полностью заряжать конденсатор, чтобы измерить его, если вы начинаете с разряженного состояния, измеряете период зарядки и записываете напряжение, достигнутое за этот период, вы можете выполнить расчет, но чем дольше (медленнее) вы тем более точным будет ваш результат, потому что ваши ошибки и т. д. будут иметь меньшее значение. Когда наименьшая цифра на вашем измерителе, измеряющем напряжение на конденсаторе, меняется раз в секунду, это было бы разумным моментом для остановки. Имейте также в виду, что конденсаторы имеют заведомо большой допуск (+/- 30% вполне нормально для некоторых типов конденсаторов).
Вы можете использовать поля в примере, чтобы выполнить свои собственные расчеты, изменить числа, чтобы увидеть, как все работает.
Пример
Конденсатор начинает разряжаться, через 60 секунд конденсатор измеряет 4,5В.
(0 — 60) / 5 / ln(1-(4,5/5)) = 5,2F
Сколько ампер-часов (Ач) в этом конденсаторе?
Ah = ( C * ( VCharged — VDepleted ) ) / 3600
Где VCharged — напряжение заряда конденсатора, VDepleted — напряжение опорожнения, а C — емкость.
Здесь вы можете видеть, что если вы используете конденсатор для замены батареи, вам действительно нужно подключить его к преобразователю постоянного тока с подходящим диапазоном входного напряжения, чтобы вы могли разрядить конденсатор до очень низкого напряжения. Возьмем наш пример выше, если вместо напряжения отсечки 3,3 В у нас будет напряжение отсечки 0,5 В, мы получим 10 мАч вместо ничтожных 2,5 мАч.
Вы можете использовать поля в примере, чтобы выполнить свои собственные расчеты, изменить числа, чтобы увидеть, как все работает.
Пример
Конденсатор 10Ф, который был заряжен до 4,2В, разряжен до 3,3В, сколько мАч?
( 10 * ( 4,2 — 3,3 ) ) / 3600 = 0,0025 Ач = 2,5 мАч
Сколько ватт-часов (Втч) в этом конденсаторе?
Втч = ( VCharged 2 — VDepleted 2 ) / (7200 / C)
Здесь видно, что если вы используете конденсатор для замены батареи, вам действительно нужно запустить его в повышающий преобразователь с подходящим диапазоном входного напряжения, чтобы вы могли разрядить конденсатор до очень низкого напряжения, взяв наш пример выше, если вместо напряжения отсечки 3,3 В у нас было бы напряжение отсечки 0,5 В, мы получили бы вместо этого 0,024 Втч.
ничтожного 0,009Wh
Вы можете использовать поля в примере, чтобы выполнить свои собственные расчеты, изменить числа, чтобы увидеть, как все работает.
Пример
Конденсатор 10Ф, который был заряжен до 4,2В, разряжен до 3,3В, сколько Втч?
((4,2 2 ) – (3,3 2 )) / (7200 / 10) = 0,009375 Втч
Сколько времени потребуется, чтобы зарядить этот конденсатор через постоянное сопротивление?
Секунды = 0 — (R * C * ln(1 — (VCharged/VSupply)))
Где VCharged — напряжение, измеренное на конденсаторе, VSupply — напряжение питания, C — емкость в фарадах, а R — резистор в Омах.
VCharged должно быть ниже VSupply — помните, чем больше заряжается конденсатор, тем выше его сопротивление зарядке, оно никогда не может сравняться с напряжением питания, даже если оно неизмеримо меньше, оно всегда меньше.
Вы можете использовать поля в примере, чтобы выполнить свои собственные расчеты, изменить числа, чтобы увидеть, как все работает.
Пример
Конденсатор 10Ф последовательно подключен к резистору 5 Ом, подключенному к источнику питания 5В. Сколько времени потребуется, чтобы конденсатор зарядился до 4,999В?
0 — ( 5 * 10 * ln(1-(4,999/5)) = 426 Секунд.
Сколько времени потребуется, чтобы разрядить этот конденсатор через постоянное сопротивление?
Секунды = 0 — (R * C * ln(VDepleted/VCharged))
Где VCharged — начальное напряжение конденсатора, VDepleted — конечное напряжение, которое вы определите как пустое, R — сопротивление, C — емкость.0003
VDepleted должен быть больше нуля — помните, что ваша схема реального мира, вероятно, не может ничего сделать с чем-либо, даже отдаленно близким к нулю.
Вы можете использовать поля в примере, чтобы выполнить свои собственные расчеты, изменить числа, чтобы увидеть, как все работает.
Пример
Конденсатор 10Ф разряжается с 5В до 0,8В через резистор 5 Ом, сколько времени это занимает?
0 — ( 5 * 10 * ln( 0,8/5)) = 91,6 секунды
Сколько времени потребуется для зарядки/разрядки этого конденсатора постоянным током?
Секунды = ( C * (VCharged — VDepleted)) / Ампер
Где C в фарадах, VCharged — начальное напряжение на конденсаторе, VDepleted — конечное напряжение разряда, а Amps — ток в амперах .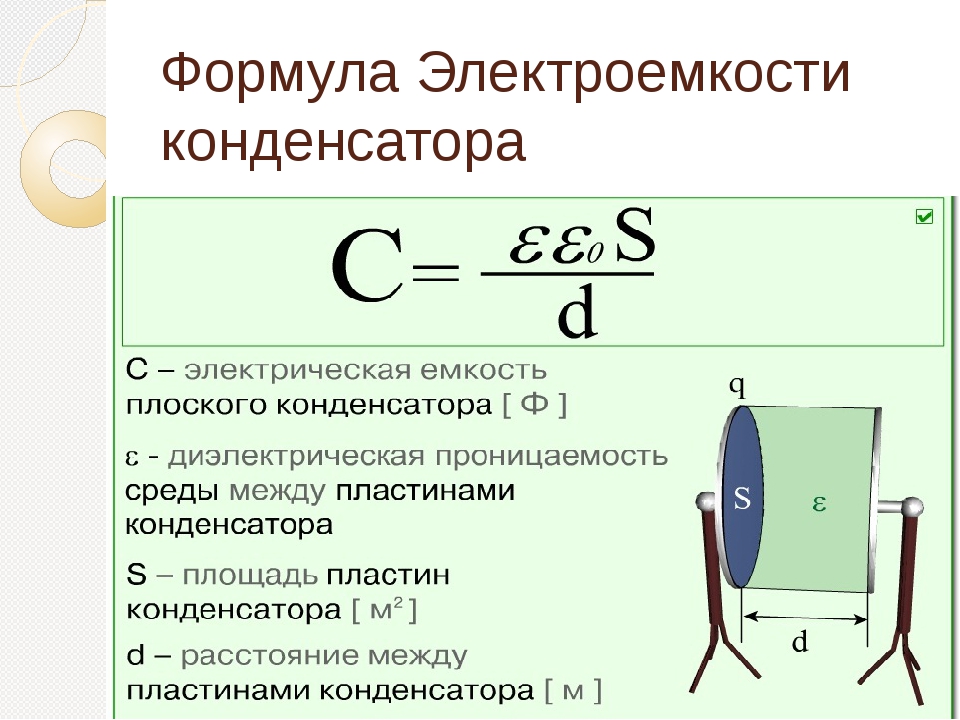
Для постоянного тока формула одинакова, независимо от того, разряжаете вы или заряжаете, важна разница напряжения, насколько напряжение должно подняться или упасть.
Вы можете использовать поля в примере, чтобы выполнить свои собственные расчеты, изменить числа, чтобы увидеть, как все работает.
Пример
Конденсатор 10Ф разряжается с 5В до 4В при постоянном токе 500мА, сколько времени это занимает?
(10 * (5 — 4)) / 0,5 = 20 секунд (расчет)
Сколько времени потребуется для зарядки/разрядки этого конденсатора при постоянной мощности (Вт)?
Секунды = 0,5 * C * ( (VCharged 2 — VDepleted 2 ) / Watts )
Где C в фарадах, VS — начальное напряжение на конденсаторе, VC — напряжение окончания разряда , а P — мощность разряда в ваттах
Вы можете использовать поля в примере, чтобы выполнить свои собственные расчеты, изменить числа, чтобы увидеть, как все работает.
Пример
Конденсатор 10Ф разряжается с 5В до 4В при постоянной мощности 2Вт, сколько времени это занимает?
0,5 * 10 * ((5 2 — 4 2 ) / 2 ) = 22,5 секунды
У меня есть батарея/ячейка емкостью несколько ампер-часов, какой емкости мне нужно, чтобы заменить ее напрямую?
C = (Ач * 3600) / (VCharged — VDepleted)
Наивно мы можем предположить, что VCharged равно номинальному напряжению вашей батареи, а VDepleted равно нулю, или, что более практично, VCharged — это максимальный уровень заряда вашей батареи, а VDepleted — это минимальное напряжение, которое может использовать ваша схема.
Вы можете использовать поля в примере, чтобы выполнить свои собственные расчеты, изменить числа, чтобы увидеть, как все работает.
Пример
Щелочная батарея емкостью 1250 мАч с полным напряжением 1,5 В и пустым напряжением 0,8 В должна быть заменена конденсатором, какой емкости он должен быть?
(1,25 * 3600) / (1,5 — 0,8) = 6428 F
Очевидно, что это нецелесообразно, поэтому см. следующий раздел… емкость мне нужно заменить его, если я использую преобразователь постоянного тока?
C = 7200 / ((VCharged 2 — VDepleted 2 ) / ((Ah * VBattery) / 0,75 ))
0,75 — это (наихудший случай) КПД преобразователя постоянного тока в постоянный, VCharged — напряжение заряженного конденсатора, VDepleted — наименьшее напряжение конденсатора, с которым может работать ваш преобразователь постоянного тока.
Вы можете использовать поля в примере, чтобы выполнить свои собственные расчеты, изменить числа, чтобы увидеть, как все работает.
Пример
Щелочная батарея емкостью 1250 мАч с номинальным напряжением 1,5 В должна быть заменена конденсатором (батареей), который заряжается до 10,8 В и управляется понижающим преобразователем, который принимает входное напряжение до 1,6 В.
7200/((10,8 2 -1,6 2 )/((1,25*1,5)/0,75)) = 157F
Я хочу получить x ампер за t секунд, какая емкость мне нужна?
C = (Amps * Seconds) / (VCharged — VDepleted)
Где C — требуемая емкость, Amps — требуемый ток, VCharged — начальное напряжение, до которого вы зарядили конденсатор, а VDepleted — минимальное напряжение, которое вы будет развлекать. Помните, как только вы получаете ток от конденсатора, его напряжение падает, вот как это работает, поэтому вы не можете просто сказать: «Я хочу 1 ампер на X вольт», вы должны сказать, что я буду потреблять ампер и может сделать это между этим и этим напряжением.
Вы можете использовать поля в примере, чтобы выполнить свои собственные расчеты, изменить числа, чтобы увидеть, как все работает.
Пример
Вы хотите получить 500 мА от конденсатора, заряженного до 12 В, в течение 5 секунд, после чего конденсатор будет измерять 9 В. Какого размера должен быть конденсатор?
(0,5 * 5) / (12 — 9) = 0,83F
Я хочу рисовать x Вт за t секунд, какая емкость мне нужна?
C = (Секунды * 2) / ((VCharged 2 — VDepleted 2 ) / Watts )
Где C — емкость, Watts — мощность в ваттах, VCharged — начальное напряжение, до которого вы зарядили конденсатор, а VDepleted — минимальное напряжение, которое вы можете поддерживать. Помните, как только вы потребляете ток от конденсатора, его напряжение падает, так это работает, поэтому вы не можете просто сказать: «Я хочу 1 ватт на X вольт», вы должны сказать, что я буду потреблять ватт и может сделать это между этим и этим напряжением.
Вы можете использовать поля в примере, чтобы выполнить свои собственные расчеты, изменить числа, чтобы увидеть, как все работает.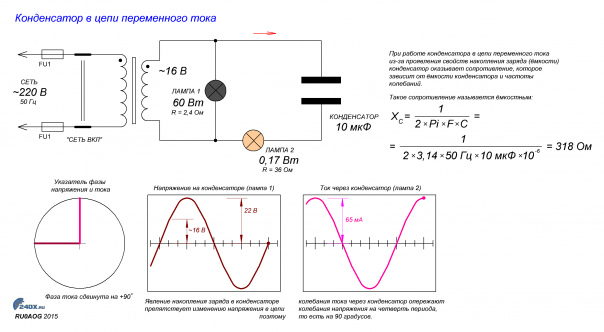
Пример
Вы хотите подать 10 Вт в течение 5 секунд от конденсатора, первоначально заряженного до 12 В, а затем измеряющего 9 В, насколько большим должен быть конденсатор?
(5 * 2) / ((12 2 — 9 2 ) / 10 ) = 1,6F
Как вы пришли к этой формуле?
В представленной формуле нет ничего особенного, одна хорошая ссылка для упрощения — это документ от ELNA, производителя суперконденсаторов, в котором рассматриваются основные уравнения для постоянного тока, мощности и сопротивления разряда.
Electronics-Tutorials.ws предоставляет разряд постоянного сопротивления, а заряд постоянного сопротивления также задается там посредством Vc = Vs(1-e -t/RC ), которым можно манипулировать, чтобы найти t (см. Видео ниже ).
Это видео от Пола Уэсли Льюиса помогло моему мозгу, лишенному математики, начать управлять манипуляциями.
Следующие онлайн-калькуляторы были полезны для подтверждения моей работы. Обязательный расчет, Circuits.
dk, bitluni.net (ВНИМАНИЕ, расчет Втч на сайте bitluni неверен, если у вас минимальное напряжение> 0)
Из этих уравнений и ресурсов получается следующее.
Расчет для ампер-часов
Начните с данной формулы для разряда постоянным током, установите t = 3600 секунд и решите, что I равно количеству ампер, которое требуется для разрядки конденсатора за это время и, следовательно, ампер-часам
секунды = (C * (VCharged — VDepleted)) / I
3600 = (C * (VCharged — VDepleted)) / I
I * 3600 = ( C * (VCharged — VDepleted))
I = ( C * (VCharged — VDepleted)) / 3600
(I = Ах)
Вычисление для ватт-часов
Это выводится из формулы для разряда постоянной мощности, где t = 3600 секунд, решенных для P, равного количеству ватт, необходимых для разрядки конденсатора за это время и, следовательно, ватт-часов.
Секунды = 0,5 * C * ((VCharged 2 — VDepleted 2 )/P)
3600 = ( (VCharged 2 — VDepleted 2 ) / P ) * C * 0,5
3600/0,5 = ( (VCharged 2 — VDepleted 2 ) / P ) * C
7200 = ( (VCharged 2 — VDepleted 2 ) / P ) * C
7200 / C = (VCharged 2 — VDepleted 2 ) / P
P*(7200 / C)= (VCharged 2 — VDepleted 2 )
P = (VCharged 2 — VDepleted 2 ) / (7200/C)
(П = Втч)
Вывод для эквивалента батареи в ампер-часах
Это просто решение уравнения для ампер-часов для емкости
Ач = ( C * (VCharged — VDepleted)) / 3600
Ач* 3600 = C * (VCharged — VDepleted)
(Ач * 3600) / (VCharged — VDepleted) = C
Вычисление для эквивалента аккумуляторной батареи в ампер-часах с преобразователем постоянного тока
Мы используем уравнение для ватт-часов, полученное выше, заменяя ватт-часы данными Ач и эквивалентным напряжением батареи, скорректированными на эффективность 75% для повышающего преобразователя.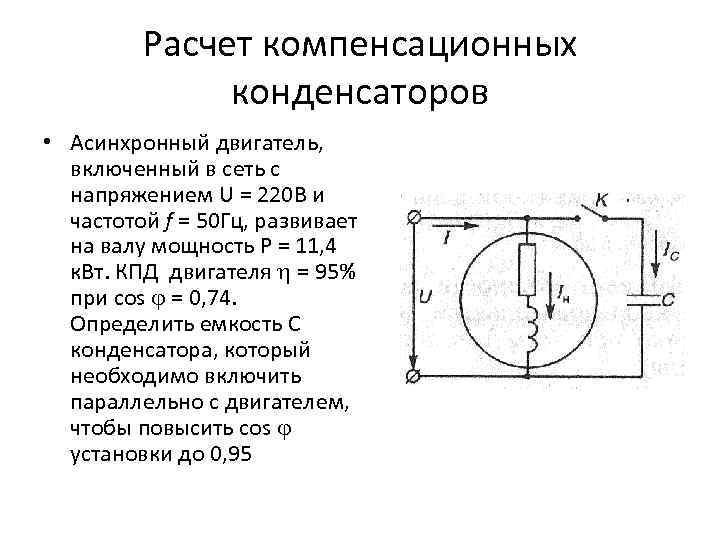
Втч = (VCharged 2 — VDepleted 2 ) / (7200/C)
( (Ач * VBattery) / 0,75 ) = (VCharged 2 — VDepleted 2 ) / (7200/C)
7200/C = (VCharged 2 — VDepleted 2 ) / (A·ч * VBattery)
7200 = C * ((VCharged 2 — VDepleted 2 ) / ( Ah * VBattery ))
7200 / ((VCharged 2 — VDepleted 2 )/ ( Ah * VBattery)) = C
Вывод для чертежа X ампер для T секунд
Простое решение приведенного уравнения постоянного тока, решение для C
секунды = (C * (VCharged — VDepleted)) / I
секунды * I = C * (VCharged — VDepleted)
(Секунды * I) / (VCharged — VDepleted) = C
Вывод для чертежа X Вт за T секунд
Простое решение приведенного уравнения постоянной мощности, решение для C
Секунды = 0,5 * C * ((VCharged 2 — VDepleted 2 )/P)
секунды = C * ((VCharged 2 — VDepleted 2 ) / P ) * 0,5
Секунды * 2 = C * ((VCharged 2 — VDepleted 2 ) / P )
(Секунды * 2) / ( (VCharged 2 — VDepleted 2 ) / P ) = C
Конденсатор i-v уравнение в действии
Конденсатор является одним из идеальных элементов схемы.
Давайте применим уравнение для конденсатора $i$-$v$, чтобы увидеть, что произойдет с напряжением, если мы добавим ток.
Автор Вилли Макаллистер.
Содержимое
- Реакция напряжения на импульс тока
- Перед пульсом
- Во время импульса
- После импульса
- Всего ответов
- Имитационная модель
- Задача дизайна
Куда мы движемся
Постоянный ток, подаваемый в конденсатор, создает напряжение с прямолинейным нарастанием. Такое поведение предсказывается интегральной формой уравнения конденсатора $i$-$v$.
Обычное уравнение конденсатора $i$-$v$ представляет собой зависимость $i$ от $v$ в производной форме, 9{\,T} i\,dt + v_0$
$v_0$ — напряжение на конденсаторе в начале интеграла, при $t=0$.
Обозначение времени немного сложное,
Маленький $t$ — непрерывная временная переменная внутри интеграла.
Большой $T$ — это момент, когда вы хотите узнать напряжение на конденсаторе.
$T$ — верхний предел интеграла.
$i = \text C\,\dfrac{dv}{dt}$
$d$ — это исчисление для «дифференциала» или «маленького изменения в…». Например, $dt$ означает «мизерное изменение во времени». Когда вы видите его в соотношении, таком как $dv/dt$, это означает «крошечное изменение $v$ (напряжения) для каждого крошечного изменения $t$ (времени)». Выражение, подобное $dv/dt$, производная. Производная измеряет скорость изменения напряжения во времени (наклон напряжения в зависимости от времени). 9{\,T} i\,dt + v_0$
Петля $\int$ — еще один символ исчисления. Это интегральный признак. Его значение аналогично символу суммирования Sigma $\Sigma$. Интегрирование противоположно взятию производной.
В уравнении конденсатора знак интеграла означает, что вы складываете последовательность произведений $(i \times dt)$ или (current $\times$ крошечный интервал времени). Когда вы видите верхний и нижний пределы символа интеграла, это делает его 90 453 определенным интегралом 90 454.
Это означает интегрировать по определенному диапазону $t$. Вы начинаете в момент времени $t=0$ и останавливаетесь в момент времени $t=T$. 9{\,T} i\,dt + v_0$
Текущий импульс имеет резкие изменения, поэтому мы собираемся найти $v(t)$ в трех отдельных фрагментах: до, во время и после текущего импульса.
Перед импульсом
Перед импульсом тока $(t < 0)$ ток не течет, поэтому на $\text C$ не накапливается заряд. Следовательно, $v_{(t<0)} = 0$. Нам даже не пришлось использовать уравнение.
Во время импульса
В любое время в течение импульса тока $(0 \lt t \lt 3\,\text{ms})$ протекает ток, на $\text C$ накапливается заряд, а напряжение возрастает. Примените уравнение конденсатора, чтобы найти, что происходит с напряжением, 9{\,T} i\,dt + v_0$
Обратите внимание на временные переменные. Маленький $t$ — это непрерывное время, переменная, которая интегрируется. Большой $T$ — это время, в течение которого может накапливаться заряд. Определенный интеграл пролистывает время $t$ от $0$ до некоторого времени накопления, большого $T$.
Чтобы найти напряжение в конце импульса, присвоим большой $T$ значение $3\,\text{ms}$.
$i$ постоянна (вершина импульса плоская) в течение этого времени, поэтому мы можем вынести ее за пределы интеграла. Мы сказали, что конденсатор начал с заряда $0$, поэтому $v_0$ равен нулю, и мы можем его не указывать. 9{-6}\,\text F} = 2000\,\text{вольт/сек}$
Для любой ширины импульса напряжение равно,
$v(T) = 2000 \,\text{вольт/сек } \,\cdot T$
Ширина нашего импульса $T = 3\,\text{ms}$, поэтому напряжение на конденсаторе возрастает до,
$v_{(T=3\,\text{ms })} = 2000 \,\text{вольт/сек} \,\cdot \,0,003 \,\text{сек} = 6\,\text{вольт}$
При постоянном токе $2\,\text {мА}$, напряжение на конденсаторе нарастает по прямой с наклоном $2000\,\text{вольт/сек}$. Напряжение начиналось с $0\,\text V$ и поднималось до $6\,\text{volts}$ после $3\,\text{ms}$.
После импульса
Эта часть довольно интересна, если вы не задумывались об этом раньше. После импульса ток падает до $0$.
Это означает, что заряд перестает накапливаться на конденсаторе. Это может показаться странным, но поскольку заряд не движется, заряду, накопленному на конденсаторе, некуда деваться, поэтому он остается на конденсаторе. Это означает, что мы должны ожидать, что напряжение на конденсаторе останется прежним. $q = \текст C\,v$. Константа $q$ подразумевает константу $v$.
Посмотрите, как математика фиксирует это, написав уравнение конденсатора после окончания импульса. 9{\,T} 0\,dt + 6$
Интеграл оценивается как $0$, и мы получаем,
$v(T) = 6\,\text V\quad$ для любого значения $T$.
После прекращения тока заряд сохраняется, поэтому напряжение на конденсаторе остается постоянным на уровне $6\,\text В$. Он остается там навсегда.
Общий отклик
Объединение трех фрагментов вместе дает нам $v(t)$ на нижнем графике,
Эта конфигурация схемы (источник тока, питающий конденсатор) имеет прозвище. Это называется интегратор , потому что он накапливает или интегрирует заряд с течением времени.
Он часто используется для создания пилообразного напряжения.
Имитационная модель
Найдите ток и напряжение с помощью этой имитационной модели. Откройте ссылку и щелкните TRAN в верхней строке меню, чтобы выполнить переходную симуляцию. Источник тока моделируется как одиночный ИМПУЛЬС. (Дважды щелкните текущий источник, чтобы увидеть, как он определяется.) Элементы управления масштабированием находятся в левой части окна и отображаются светло-серым цветом.
Вот еще одна имитационная модель с источником тока, определенным другим способом, как форма волны PWL (кусочно-линейная). Время и ток вводятся в виде списка разделенных запятыми пар [время, ток], например: -1 с, 0, 0 с, 0, 1 нс, 2 м, 3 мс, 2 м, 3 мс, 0, 5 с, 0.
Посмотрите, можете ли вы изменить форму кривой тока, чтобы напряжение на конденсаторе снизилось до $0\text V$ еще за $3\,\text{ms}$. Вы собираетесь сделать что-то похожее на это:
показать ответ Дважды щелкните текущий источник и введите это в PWL «список чередующихся значений времени и значений, разделенных запятыми».