Расчет объема по воды по сечению трубы: Расчет объема воды в трубе по формуле + готовая таблица

Как рассчитать объём воды в трубах

Как рассчитать объём воды в трубах

Сколько воды расходуется по статье «общедомовые нужды»

при сбросе стояков?

Как выбрать гидроаккумулятор?

Сколько антифриза покупать для заполнения системы отопления коттеджа?

ПАМЯТКА

как рассчитать объем воды в трубе

Объем воды в трубах вычисляется как сумма произведений объемов воды в метре трубы каждого диаметра на количество метров труб данного диаметра.

Объем гидроаккумулятора для системы отопления должен составлять 10-12 % объема всей воды в системе. Последняя цифра складывается из объема воды во всех радиаторах отопления, плюс объема воды в котле отопления, плюс объем воды в трубах для отопления.

Объем воды в радиаторах складывается из объема воды в каждой секции радиатора, помноженном на количество секций. Это значение указывается в технических паспортах на радиаторы.

Смотрим технический паспорт.

Объем воды в котле отопления указывается в паспорте. Этот объем полезно знать также при спуске воды из отдельных частей системы отопления.

Таблица объема воды

в неармированных и армированных алюминием полипропиленовых трубах:

Номинальный размер (внешний диаметр), мм	Внутреннее сечение, мм кв.	Объем воды в метре трубы, литры	Внутренний диаметр, мм	Соответствующий им диаметр стальных дюймовых труб, дюймы
20	136,7	0,137	13,2	1/2
25	216,3	0,216	16,6	3/4
32	352,8	0,353	21,2	1
40	555,4	0,555	26,6	1 1/4 (дюйм с четвертью)
50	865,3	0,865	33,2	1 1/2
63	1384,7	1,385	42	2
75	1962,5	1,963	50	2 1/2
90	2826	2,826	60	3
110	4206,2	4,206	73,2

Таблица объема воды в стальных трубах:

Номинальный размер, дюймы	Внешний диаметр, мм	Внутренний диаметр, мм	Внутреннее сечение, мм	Объем воды в метре трубы, литры
1/4	13,5	9,5	29,83	0,03 (30 миллилитров)
3/8	17	13	133	0,133
1/2 (полдюйма)	21,3	16,3	209	0,209
3/4	26,8	21,8	373	0,373
1	33,5	27,9	611	0,611
1 1/4 (дюйм с четвертью)	42,3	36,7	1057	1,057
1 1/2	48	42	1385	1,385
2	60	54	2289	2,289

Объем воды в стальных трубах больше количества воды в соответствующих пластиковых трубах Внутренняя поверхность пластиковых труб гладкая, а стальных труб шероховатая. В результате пластиковые трубы (как и медные) меньшего диаметра пропускают столько же воды, сколько и стальные трубы, имеющие больший внутренний диаметр.

Генеральный директор

ООО «ОСТРОУМОВ» Д.Ю. Остроумов

Рассчитать объем воды в трубе с помощью онлайн калькулятора

Трубы настолько широко применяется в народном хозяйстве, что перечислить все направления их использования просто невозможно. И очень часто нужно определить объем трубы, для чего применяется онлайн калькулятор. Используя этот инструмент можно быстро и достаточно точно высчитать объем единичного изделия или цельного трубопровода любой протяжённости.Предлагаем вам воспользоваться нашим бесплатным онлайн калькулятором для определения объема воды в трубе.

При расчете Вы узнаете объем воды или любой другой жидкости в одном метре трубы, так же сможете рассчитать объем во всем трубопроводе и площадь поверхности рассчитываемого участка.

Содержание

1. Введите параметры для расчёта в онлайн калькулятор
2. Как произвести расчет без калькулятора
3. Расчёт объёма трубы
4. Формула для расчёта объёма трубы
5. Определим площадь сечения трубы
6. Формула расчёта объёма трубы
7. Объём водопровода в литрах

Введите параметры для расчёта в онлайн калькулятор

Предлагаем ввести параметры в для расчета объёма в онлайн калькулятор.

Наружный диаметр трубы D,мм
Длина участка магистрали L,м
Толщина стенки S,мм

   

Почему необходимо заранее рассчитать объем жидкости в трубе калькулятором, только после этого приступать к закупкам? Ответ очевиден – для того чтобы определить, сколько надо приобрести теплоносителя, чтобы заполнить систему отопления дома. Особенно это важно для домов периодического посещения, которые на длительное время остаются холодными. Вода внутри такой отопительной системы неминуемо замерзнет, разрывая проводящие элементы и радиаторы. Кроме того, нужно учитывать и моменты которые перечислены в расположенном ниже списке.

• Вместимость расширительного бачка. Этот параметр всегда указывается в паспорте на это изделие, но если такая возможность отсутствует, можно просто заполнить емкость определенным количеством литров воды, после чего использовать эту информацию.
• Емкость нагревательных элементов – радиаторов отопления. Такие данные также можно получить из технического паспорта или инструкции для одной секции. После чего, воспользовавшись проектными данными, умножить емкость одной секции на их общее число.
• Количество жидкости внутри различных узлов, а также системах управления и контроля, например – тепловых насосов, манометрах и тому подобное. Впрочем, эта величина будет небольшой, не выше статистической погрешности, поэтому данные третьего пункта обычно игнорируют.

Если система водоснабжения или отопления выполняется из металлических изделий, нужно учитывать некоторые их особенности. Так, водогазопроводный сортамент по ГОСТ 3262-84 выпускается трех серий:

• легкая;
• средняя;
• тяжелая.

При этом различие состоит именно по толщине стенок, что при равенстве внешнего размера, говорит об уменьшении внутреннего сечения для разных исполнений. Поэтому при закупке следует обращать внимание именно на этот показатель, чтобы внутренний проход был одинаков по всей протяженности водопровода или отопления. Расчет объема жидкости в трубе, с использованием калькулятора можно произвести, воспользовавшись следующей формулой:

1. V – объем метра трубы, см3.
2. 100 – длина, см.
3. Число «пи», равное 3.14.
4. Радиус внутреннего канала, см. здесь — площадь поперечного сечения внутренней полости.

При расчете нужно руководствоваться не сертификатными данными или вывеской продавца. Желательно тщательно измерить размер внутреннего отверстия, используя штангенциркуль, а при подсчете руководствоваться именно этими данными.

Если конструкция этого измерительного прибора не позволяет производить внутренние замеры, можно мерить наружный диаметр и толщину стенки. Затем первого замера нужно вычесть удвоенный второй, после чего получить достоверный размер проходного отверстия.

Кроме принадлежности к одной серии, о чем упоминалось выше, нужно учитывать возможность использования исходного материала на минусовых допусках, что закономерно повлияет на размер сечения в сторону его увеличения. Если есть возможность воспользоваться при закупке интернетом, можно использовать встроенный программный calculator, рассчитать объем воды в трубе онлайн. Но при этом исходные данные нужно водить реальные. Настоятельно рекомендуем перед использованием калькулятора ознакомиться с инструкцией, в таком случае расчеты будут верными со стопроцентной гарантией.

С их использованием должны рассчитываться также другие параметры системы, включая вес погонного метра и прочее. Широкое применение при выполнении таких операций нашли специально разработанные таблицы. Но они справедливы только для номинальных размеров, любые отклонения они не учитывают. Определяя объем воды в трубе онлайн калькулятором, ошибиться маловероятно.

Как произвести расчет без калькулятора

Трубопроводный транспорт в условиях России играет очень важную роль. По нему перекачиваются огромные количества жидких продуктов. Кроме воды транспортируется сжиженный газ, нефть и продукты её переработки и другие жидкости, в ряде случаев агрессивные.

Алгоритм расчёта вместимости трубы несложен – нужно узнать площадь поперечного сечения и умножить её на длину изделия. Она определяется условиями её транспортировки по железной дороге, база вагона равняется 11,7 метра, поэтому они производятся длиной 11,3-11,7 м.

Вместимость такого изделия определяется диаметром внутреннего пространства, например для размера 820 х 10 миллиметров рабочий диаметр мы можем определить соотношением Д = 820 – 10 х 2 = 800 мм. Однако, лучше сразу перейти к общепринятой единице – метру. При внутреннем диаметре изделия 0,8 метра соотношение для расчёта выглядит следующим образом:

V = П*r2l

где:

• V – объем;
• П – число пи, равное 3,14;
• r – радиус;
• l – её длина.

Однако высчитывать объем одиночного изделия не имеет смысла. Лучше сразу применить это соотношение для определения объёма всего трубопровода.

Этот показатель важен для того чтобы знать количества перекачиваемого продукта, которое останется в трубопроводе по окончании транспортировки нужного объема. Однако трубопроводы не используются в режиме разовой перекачки. Они предназначены для постоянной эксплуатации.

По такой же методике рассчитываются объёмы емкостей цилиндрической формы – цистерн, бочек и прочих подобных.

В трубопроводном транспорте для магистралей используются в основной массе электро сварные одно или двух шовные трубы с различной толщиной стенок. Для повышения производительности трубопровода продукты по нему перекачиваются под большим давлением – до 130 атмосфер.

Поэтому для производства используется листовой металл толщиной до 36 миллиметров. Основной способ соединения в трубопроводах – электросварка, поэтому в качестве материала изготовления используются  стали с низким содержанием углерода, такие, как 09Г2С, 09Г2ФБ и другие подобные.

Основным регламентирующим документом для производства электро сварных прямо шовных труб являются ГОСТы 10804 и 10805, однако применяются также множество технических параметров, предусматривающих определенные условия изготовления труб которые будут эксплуатироваться в агрессивной среде.

Важным направлением применения труб являются вентиляционные системы промышленного и бытового назначения. Для обеспечения прочностных показателей в них чаще всего используются прямоугольные короба, рассчитывать вместимость которых гораздо проще.

Коробчатые трубопроводы для вентиляции производятся, как правило, из оцинкованной стали, имеющей длительный срок эксплуатации. Но в последнее время наметилась тенденция применение для вентиляционных систем из пластиковых материалов, срок службы которых может превышать этот показатель для металлических аналогов.

Это же относится к использованию пластиков для водопроводных напорных и самотёчных систем.

Точное определение объёма труб и трубопроводов из них доступно всем пользователям сети Интернет и это позволяет избежать серьёзных ошибок при проектировании самых различных объектов народного хозяйства.

Расчёт объёма трубы

Для расчёта объёма трубы нужно воспользоваться школьными знаниями по геометрии. Есть несколько способов: 1.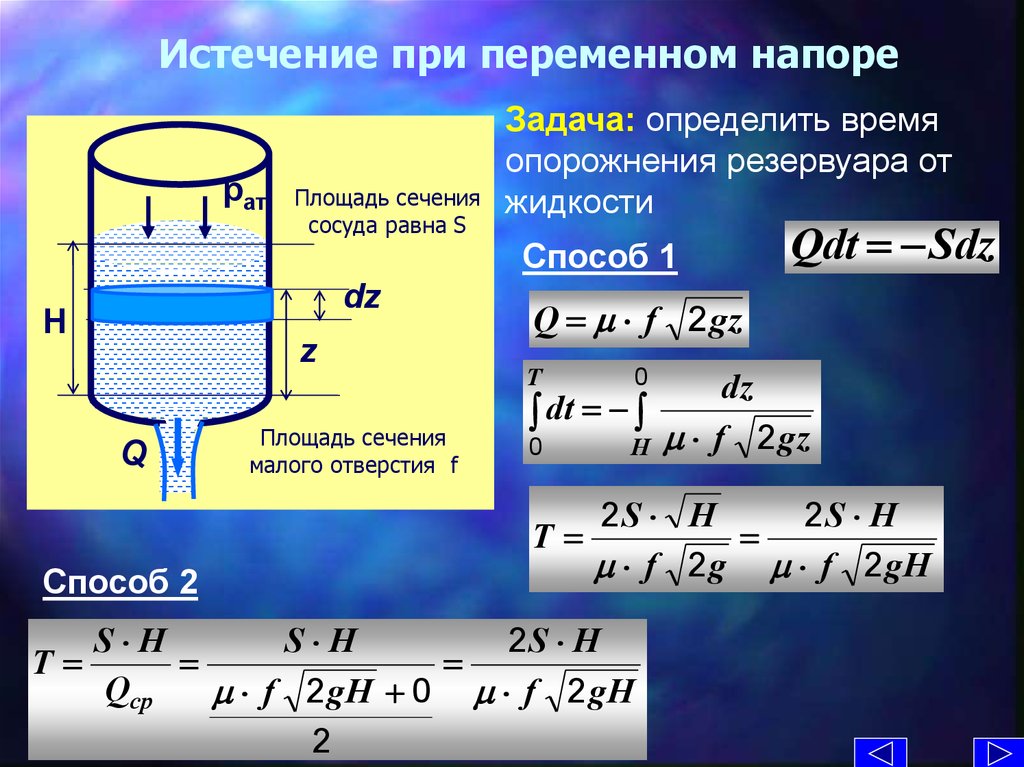 Умножив площадь поперечного сечения фигуры на её длину в метрах, полученный результат будет метры в кубе. 2. Возможно, узнать величину водопровода и в литрах. Для этого объём умножается на 1000 — это количество литров воды в 1 кубометре. 3. Третий вариант — сразу считать в литрах. Понадобится измерения делать в дециметрах — длину и площадь фигуры. Этот более сложный и неудобный способ.

Чтобы вычислить в ручную – без калькулятора, потребуется штангенциркуль, линейка и калькулятор. Для облегчения процесса по определению размера объёма трубы можно воспользоваться онлайн-калькулятором.

Формула для расчёта объёма трубы

Процесс расчёта объёма системы отопления выглядит следующим образом.

Определим площадь сечения трубы

Чтобы узнать точное значение, необходимо сначала рассчитать площадь поперечного сечения. Для этого, следует воспользоваться формулой:

S = R2 х Пи

Где R является радиусом трубы, а число Пи равно 3,14. Так как ёмкости для жидкости,как правило, имеют круглую форму, то R возводится в квадрат.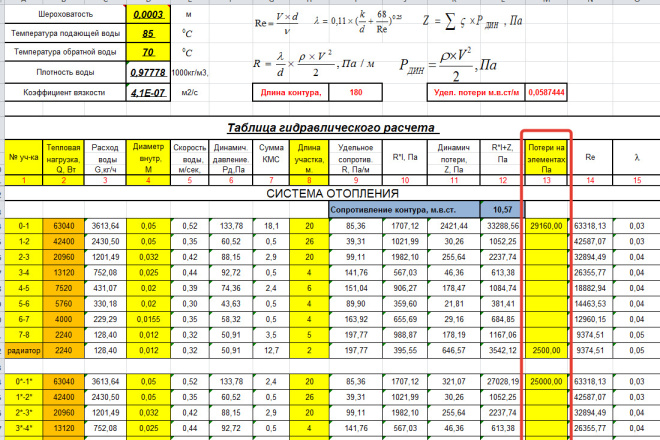

Рассмотрим, как можно сделать вычисления, имея диаметр изделия 90 мм:

1. Определяем радиус — 90 / 2 = 45 мм, в пересчёте на сантиметры 4,5.
2. Возводим 4,5 в квадрат, получается 2,025 см2.
3. Подставляем данные в формулу — S = 2 х 20,25 = 40, 5 см2.

Если изделие профилированное, то нужно считать по формуле прямоугольника — S = а х b, где а и b — размер сторон (длина). При определении размера сечения профиля с длиной сторон 40 и 50, необходимо 40 мм х 50 мм = 2000 мм2 или 20 см2.

Для вычисления сечения, необходимо знать внутренний диаметр трубы, который измеряется штангенциркулем, но это не всегда возможно. Если известен только наружный диаметр, и не знаем толщину стен, то потребуются более сложные вычисления. Стандартная толщина бывает 1 или 2 мм, у изделий большого диаметра может достигать 5 мм.

Важно! Приступать к расчёту лучше при наличии точных показателей о толщине стен и внутреннем радиусе.

Формула расчёта объёма трубы

Рассчитать объём трубы в м3, можно воспользовавшись формулой:

 V = S х L

То есть, требуется знать всего два значения: площадь сечения (которая была определена заранее) (S) и длина (L).

К примеру, длина трубопровода 2 метра, а площадь сечения пол метра. Для вычисления необходимо взять формулу, по которой определяется площадь круга, и вставить внешний размер поперечины металла:

S = 3,14 х (0,5 / 2) = 0,0625 кв.м.

Итоговый результат будет следующим:

V = HS = 2 х 0,0625 = 0,125 метра куб.

H — толщина стенки

Производя расчёт, важно чтобы во всех показателях была одна единица измерения, иначе результат получится неправильным. Проще брать данные в см2.

Объём водопровода в литрах

Легко посчитать объём жидкости в трубе без калькулятора, если знать внутренний её диаметр, но это не всегда можно сделать, когда радиаторы или отопительные котлы для воды имеют сложную форму. Сегодня такие изделия не редко применяются в строительной сфере, при обустройстве тёплых полов. Поэтому, следует изначально выяснить параметры конструкции, эту информацию можно найти в техпаспорте или сопроводительной документации. Чтобы посчитать размер не стандартной емкости, необходимо залить в неё воду, которая заранее измерена.

Кроме того, кубатура воды будут зависеть и от материала, из которого изготовлен водопровод. К примеру, изделие из стали пропустит на порядок меньше воды, чем равное по размеру полипропиленовое или пластиковое. На это влияет поверхность изнутри, железная более шероховатая, что сказывается на проходимости.

Поэтому, необходимо делать вычисления на каждую ёмкость, если она изготовлена из другого материала, и затем сложить все показатели. Можно воспользоваться специальными сервис-программами или калькуляторами, сегодня их много в интернете, они существенно облегчат процесс установления количества воды в системе.

12.1 Расход и его связь со скоростью – College Physics: OpenStax

Глава 12 Динамика жидкости и ее биологические и медицинские приложения

Сводка

• Рассчитать скорость потока.
• Определить единицы объема.
• Опишите несжимаемые жидкости.
• Объясните следствия уравнения неразрывности.

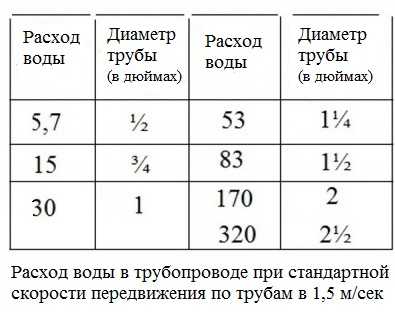
Скорость потока [латекс]\boldsymbol{Q}[/латекс] определяется как объем жидкости, проходящей через некоторое место через область в течение периода времени, как показано на рисунке 1. В символах это может быть пишется как 93}[/латекс]). В этом тексте мы будем использовать любые метрические единицы, наиболее удобные для данной ситуации.

Рисунок 1. Расход – это объем жидкости в единицу времени, протекающий через точку через площадь A . Здесь заштрихованный цилиндр жидкости течет мимо точки P по однородной трубе за время t . Объем цилиндра равен Ad , а средняя скорость равна v̄=d/t , так что расход равен Q=Ad/t=Av̄ .

Пример 1. Расчет объема по скорости кровотока: сердце перекачивает много крови за всю жизнь

Сколько кубических метров крови перекачивает сердце за 75 лет жизни, если предположить, что средняя скорость кровотока составляет 5,00 л/мин?

Стратегия

Время и скорость потока[latex]\boldsymbol{Q}[/latex] даны, поэтому объем[latex]\boldsymbol{V}[/latex]может быть рассчитан из определения потока ставка.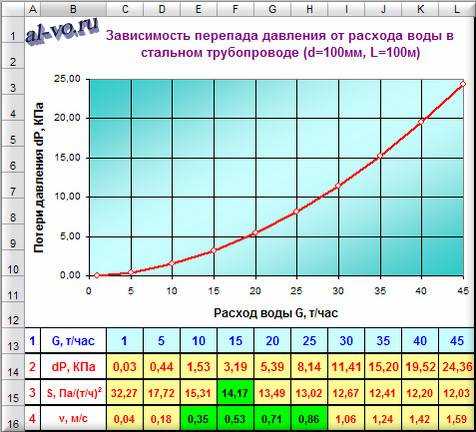

Решение 93.} \end{array}[/latex]

Обсуждение

Это количество составляет около 200 000 тонн крови. Для сравнения, это значение примерно в 200 раз превышает объем воды, содержащейся в 50-метровом плавательном бассейне с 6 дорожками.

Расход и скорость являются связанными, но совершенно разными физическими величинами. Чтобы прояснить различие, подумайте о скорости течения реки. Чем больше скорость воды, тем больше расход реки. Но скорость течения также зависит от размера реки. Быстрый горный поток несет гораздо меньше воды, чем, например, река Амазонка в Бразилии. Точное соотношение между скоростью потока[латекс]\жирныйсимвол{Q}[/латекс]и скоростью[латекс]\жирныйсимвол{\бар{в}}[/латекс] равно 9.0005

[латекс]\boldsymbol{Q=A\bar{v}},[/латекс]

, где[латекс]\жирныйсимвол{А}[/латекс]– площадь поперечного сечения, а[латекс]\жирныйсимвол{\бар{в}}[/латекс]– средняя скорость. Это уравнение кажется достаточно логичным. Соотношение говорит нам, что скорость потока прямо пропорциональна как величине средней скорости (далее называемой скоростью), так и размеру реки, трубы или другого водовода. Чем больше трубопровод, тем больше его площадь поперечного сечения. Рисунок 1 иллюстрирует, как получается это соотношение. Заштрихованный цилиндр имеет объем

[латекс]\boldsymbol{V=Ad},[/латекс]

, который проходит мимо точки[latex]\textbf{P}[/latex]за время[latex]\boldsymbol{t}.[/latex]Разделив обе части этого соотношения на[latex]\boldsymbol{t}[ /латекс] дает

[латекс]\boldsymbol{\frac{V}{t}}[/latex][латекс]\boldsymbol{=}[/latex][латекс]\boldsymbol{\frac{Ad}{t}}.[/ латекс]

Заметим, что [латекс]\boldsymbol{Q=V/t}[/latex]и средняя скорость равна[латекс]\boldsymbol{v\bar{v}=d/t}.[/latex] Таким образом, уравнение становится [латекс]\boldsymbol{Q=A\bar{v}}.[/латекс]

На рис. 2 показано течение несжимаемой жидкости по трубе с уменьшающимся радиусом. Поскольку жидкость несжимаема, через любую точку трубки за заданное время должно пройти одинаковое количество жидкости, чтобы обеспечить непрерывность потока. В этом случае, поскольку площадь поперечного сечения трубы уменьшается, скорость обязательно должна увеличиваться. Эту логику можно расширить, чтобы сказать, что скорость потока должна быть одинаковой во всех точках трубы. В частности, по пунктам 1 и 2

[латекс]\begin{array}{c} \boldsymbol{Q_1=Q_2} \\ \boldsymbol{A_1\bar{v}_1=A_2\bar{v}_2.} \end{array}[/latex] [латекс]\rbrace[/латекс]

Это называется уравнением неразрывности и справедливо для любой несжимаемой жидкости. Следствия уравнения неразрывности можно наблюдать, когда вода течет из шланга в узкую форсунку: она выходит с большой скоростью — в этом назначение форсунки. И наоборот, когда река впадает в один конец водохранилища, вода значительно замедляется и, возможно, снова набирает скорость, когда выходит из другого конца водоема. Другими словами, скорость увеличивается, когда площадь поперечного сечения уменьшается, и скорость уменьшается, когда площадь поперечного сечения увеличивается.

Рисунок 2. Когда трубка сужается, тот же объем занимает большую длину. Чтобы один и тот же объем прошел точки 1 и 2 за заданное время, скорость должна быть больше в точке 2.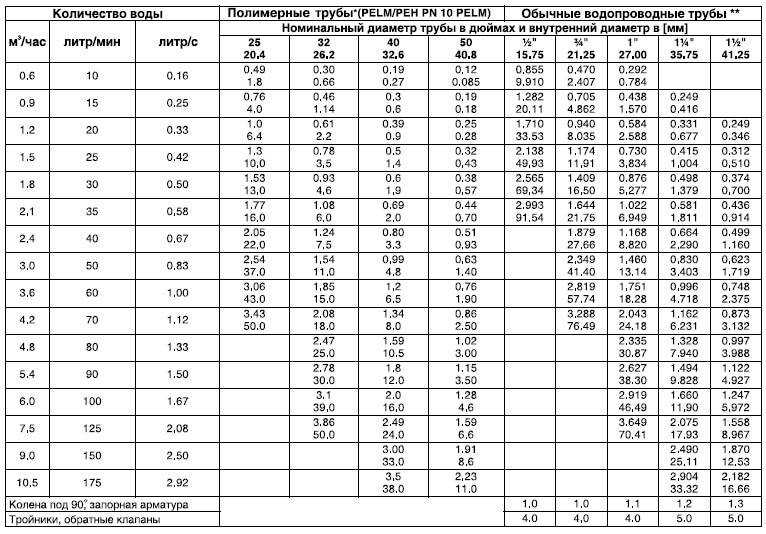 Процесс точно обратим. Если жидкость течет в противоположном направлении, ее скорость будет уменьшаться при расширении трубы. (Обратите внимание, что относительные объемы двух цилиндров и соответствующие стрелки вектора скорости нарисованы не в масштабе.)

Поскольку жидкости практически несжимаемы, уравнение неразрывности справедливо для всех жидкостей. Однако газы сжимаемы, поэтому уравнение следует применять с осторожностью к газам, если они подвергаются сжатию или расширению.

Пример 2. Расчет скорости жидкости: скорость увеличивается при сужении трубы

Насадка с радиусом 0,250 см присоединена к садовому шлангу с радиусом 0,900 см. Скорость потока через шланг и сопло составляет 0,500 л/с. Рассчитайте скорость воды (а) в шланге и (б) в насадке.

Стратегия

Мы можем использовать соотношение между расходом и скоростью, чтобы найти обе скорости. Мы будем использовать нижний индекс 1 для шланга и 2 для сопла. 92}}[/latex][latex]\boldsymbol{=\:1. 2}[/latex]вместо площади поперечного сечения, получим 92}}[/latex][latex]\boldsymbol{1,96\textbf{ м/с}=25,5\textbf{ м/с}}.[/latex]

Обсуждение

Скорость 1,96 м/с примерно подходит для воды, вытекающей из шланга без насадок. Форсунка создает значительно более быстрый поток, просто сужая поток в более узкую трубку.

Решение последней части примера показывает, что скорость обратно пропорциональна квадрату радиуса трубы, что приводит к большим эффектам при изменении радиуса. Мы можем задуть свечу на довольно большом расстоянии, например, сжав губы, тогда как задувание свечи с широко открытым ртом совершенно неэффективно.

Во многих ситуациях, в том числе в сердечно-сосудистой системе, происходит разветвление потока. Кровь перекачивается из сердца в артерии, которые подразделяются на более мелкие артерии (артериолы), которые разветвляются на очень тонкие сосуды, называемые капиллярами. В этой ситуации непрерывность потока сохраняется, но сохраняется сумма расходов расходов в каждой из ветвей на любом участке вдоль трубы. Уравнение неразрывности в более общем виде принимает вид

[латекс]\boldsymbol{n_1A_1\бар{v}_1=n_2A_2\бар{v}_2},[/латекс]

где[latex]\boldsymbol{n_1}[/latex]и[latex]\boldsymbol{n_2}[/latex]количество ответвлений на каждом из участков вдоль трубы.

Пример 3: расчет скорости кровотока и диаметра сосуда: разветвления в сердечно-сосудистой системе

Аорта является основным кровеносным сосудом, по которому кровь покидает сердце, чтобы циркулировать по всему телу. а) Рассчитайте среднюю скорость движения крови в аорте при скорости потока 5,0 л/мин. Аорта имеет радиус 10 мм. (б) Кровь также течет через более мелкие кровеносные сосуды, известные как капилляры. При скорости кровотока в аорте 5,0 л/мин скорость крови в капиллярах составляет около 0,33 мм/с. Учитывая, что средний диаметр капилляра составляет[latex]\boldsymbol{8.0\:\mu},[/latex]рассчитайте количество капилляров в системе кровообращения. 92}}[/latex][latex]\boldsymbol{=\:0.27\textbf{ м/с.}}[/latex]

Решение для (b)

Использование[latex]\boldsymbol{n_1A_1\ bar{v}_1=n_2A_2\bar{v}_1},[/latex]присваивая индекс 1 аорте и 2 капиллярам и находя[latex]\boldsymbol{n_2}[/latex](число капилляров) дает[latex]\boldsymbol{n_2=\frac{n_1A_1\bar{v}_1}{A_2\bar{v}_2}}. 93}.[/латекс]

Расход и скорость связаны соотношением[latex]\boldsymbol{Q=A\bar{v}}[/latex],где[latex]\boldsymbol{A}[/latex]является площадью поперечного сечения потока и [латекс]\boldsymbol{\bar{v}}[/латекс] — его средняя скорость.

Для несжимаемых жидкостей скорость потока в различных точках постоянна. То есть,

[латекс]\begin{array}{c} \boldsymbol{Q_1=Q_2} \\ \boldsymbol{A_1\bar{v}_1=A_2\bar{v}_2} \\ \boldsymbol{n_1A_1\bar{v }_1=n_2A_2\bar{v}_2.} \end{массив}[/latex][latex]\rbrace[/latex]

расход

, сокращенно Q , это объем V , протекающий через определенную точку за время t , или Q = V/t

литр

единица объема, равная 10 ⁻³ м ³

 

Вопрос Видео: Расчет времени прохождения воды через трубы разного радиуса

Стенограмма видео

Вода со скоростью 𝑣 1 равна 3,15 метра в секунду плавно течет по цилиндрической трубе радиусом 𝑟 1 равна 1,25 метра и затем течет плавно через вторую соединенную цилиндрическую трубу радиуса 𝑟 два равно 0,951 метр, как показано на схеме. Первая труба имеет длину 𝐿 единица равна 1,44 метра, а вторая труба имеет длину 𝐿 два равна 1,21 метра. Каково отношение времени прохождения воды по первой трубе ко времени прохождения по второй трубе?

Здесь на нашей диаграмме мы видим первую трубу длиной 𝐿 один и вторую трубу длиной 𝐿 два. Эти трубы имеют разные радиусы, 𝑟 один и 𝑟 два. И нам говорят, что скорость воды, когда она входит в первую трубу со скоростью, называемой 𝑣 один, составляет 3,15 метра в секунду. Зная это, наряду со значениями длин труб, 𝐿 один и 𝐿 два, мы хотим найти отношение времени, которое требуется воде, чтобы пройти через эту первую трубу, ко времени, которое требуется воде, чтобы пройти через эту вторую трубу. Давайте освободим место на экране и начнем с присвоения переменных этим двум значениям времени.

Предположим, что время, которое требуется воде, чтобы пройти от одного конца трубы до другого, равно 𝑡 одному, а время, которое требуется воде, чтобы пройти по второй трубе, равно 𝑡 двум. Мы пытаемся найти отношение 𝑡 один к 𝑡 двум. Всякий раз, когда несжимаемая жидкость, такая как вода, которая у нас есть здесь, течет через сосуд с жесткими стенками, когда эта жидкость течет плавно, это следует тому, что называется уравнением неразрывности. Это уравнение представляет собой утверждение о том, как объем жидкости передается через контейнер. В нем говорится, что скорость, с которой объем жидкости проходит через одно поперечное сечение сосуда, равна скорости, с которой тот же объем проходит через другое поперечное сечение сосуда. В нашем случае те поперечные сечения, о которых мы думаем, являются поперечными сечениями наших двух труб с радиусами 𝑟 один и 𝑟 два.

Уравнение неразрывности говорит о том, что объем воды, проходящий через это сечение нашей трубы за некоторый промежуток времени, скажем, одну секунду, равен объему воды, прошедшему через этот участок нашей трубы с другим радиусом за тот же промежуток времени. Сначала может быть неясно, поможет ли нам уравнение неразрывности, потому что мы хотим решить для отношения времен. Но уравнение непрерывности действительно включает скорости. 𝑣 один и 𝑣 два — скорости на входе и выходе жидкости через эту систему трубопроводов соответственно. И мы можем вспомнить, что в общем случае скорость 𝑣 объекта равна расстоянию, пройденному этим объектом, деленному на время, затраченное на преодоление этого расстояния.

Для нашей воды, когда она проходит, скажем, через первую трубу, расстояние, которое она проходит, равно 𝐿 единице, а время, необходимое для прохождения этого расстояния, равно 𝑡 единице. Аналогично, 𝑣 два, скорость выхода воды через систему труб, равна 𝐿 два, деленная на 𝑡 два. Все это означает, что мы можем записать уравнение неразрывности таким образом. Здесь 𝑣 один заменяется на 𝐿 один на 𝑡 один, а 𝑣 два заменяется на 𝐿 два на 𝑡 два. Как мы видели, это согласуется с общей формулой для скоростей. Поскольку мы пытаемся найти 𝑡 один, разделенный на 𝑡 два, давайте перестроим это уравнение так, чтобы 𝑡 один на 𝑡 два оказалось с одной стороны отдельно.

Мы можем начать делать это, умножив обе части на 𝑡 единицу, отменив множитель слева. Далее мы делим обе части уравнения на 𝐴 два раза 𝐿 два. Это приводит к тому, что 𝐴 два и 𝐿 два сокращаются с правой стороны. И когда уляжется пыль от отмен, мы получим именно то, что хотели: 𝑡 один разделить на 𝑡 два на одной стороне нашего уравнения.

Чтобы найти это отношение, нам нужно знать значения этих переменных. В условии задачи нам даны 𝐿 один и 𝐿 два. И хотя мы не знаем 𝐴 один и 𝐴 два напрямую, мы знаем радиусы 𝑟 один и 𝑟 два. А еще мы знаем, что сечения этих труб круглые. С точки зрения радиуса 𝑟 площадь круга равна 𝜋, умноженной на 𝑟 в квадрате. Тогда мы можем написать, что 𝐴 один равен 𝜋, умноженному на 𝑟 один в квадрате, а 𝐴 два равен 𝜋, умноженному на 𝑟 два в квадрате.

Обратите внимание, что в этой дроби множитель 𝜋 уравновешивается. Подстановка вместо 𝑟 одного, 𝐿 одного, 𝑟 двух и 𝐿 двух дает нам эту дробь. Как в числителе, так и в знаменателе у нас есть метры в кубе, поэтому все они сокращаются. И наш окончательный ответ будет безразмерным. Округлив эту дробь до трех значащих цифр, получим 2,06.