СофтВент: Вентиляция в 1С
Релиз 1.0.18
Дата выхода релиза 25.01.2021
Новый релиз дает возможность более точно анализировать затраты на производство продукции
- Уже доступен по запросу и в облаке «СофтВент».
- Новые настройки продукции, чертежей и индивидуальных настроек можно скачать в вашем Личном кабинете
-
1. Возможность расширить ассортимент и производить 141 элемент продукции, из которых 21 элемент с готовыми шаблонами расчета.
Внесены изменения по более чем 80 элементам продукции, по 16 разделам (Воздуховоды, Отводы, Переходы, Тройники Крестовины, Заглушки, Утки, Врезки, Зонты крышные , КСД , Шибера, Мягкие вставки, Зонты вытяжные , Окожушка , Профили и Воздухораспределители).

Полностью переработаны формулы расчета площадей
Полностью переработаны формулы расчета площадей
Отдельно считается «Площадь изделия чистая» и «Площадь изделия с замками»
Сделан расчет «Масса изделия с замками» и «Объем изделия»
Опционно реализована возможность вести учет замков в расчете площадей для коммерческого предложения и счета по любому элементу
-
2. Более детально вести внутренний учет:
появилась возможность проверки правильного списания материалов (сделан отчет по расшифровке на каждый элемент продукции)
установлены все артикулы для внутреннего учета
-
3. Возможность работать еще быстрее с основной формой:
Ускорен запуск основной формы расчета
Обновлены иконки при выборе продукции
Переработаны условные обозначения
Изменены и переработаны некоторые исходные данные для ввода продукции
-
4.
 Новые автоматические обработки
Новые автоматические обработки
Теперь для переноса настроек и создания новой продукции Вам не надо создавать отдельно «Номенклатуру» и привязывать к ней справочник «Продукция», а затем делать настройки видимости для расчета и добавлять чертежи на продукцию и на замки. Мы добавили для Вас обработки, которые позволяют легко сделать все настройки продукции, а затем и записать все чертежи и замки из файлов, которые Вам доступны в любое время в Вашем «Личном кабинете».
Обработки для автоматического переноса:
- 1. Продукции (обработка «Перенос настроек»)
- 2. Картинок (обработка «Перенос чертежей»)
После обновления релиза вы можете также и вручную добавлять ту продукцию, которая у Вас изготавливается на производстве
-
5. Кроме этого:
Запущен в разработку механизм валидации (корректного ввода исходных данных), что исключает ошибку как менеджера, обрабатывающего заявку, так и проектировщика, допустившего описку.

Прямо в форме создания продукции можно отказаться от валидации на конкретную продукцию
Будет добавлена возможность просмотра не только текстового сообщения и возможный порядок решения, но и чертеж возможного исправления по каждой возможной ошибке.
Обновленные чертежи и расчеты существующих элементов
Утки прямоугольного сечения
Утка прямоугольного сечения косая |
Утка прямоугольного сечения радиусная |
Утка прямоугольного сечения с переходом |
По многочисленным просьбам, а так же ориентируясь на ведущих произвоидителей воздуховодов и вентиляционного оборудования были изменены входящие параметры уток прямоугольного сечения:
А именно параметры «A» и «B» поменяли местами. Вместо припусков на соединение «р» установили параметры полок «l1» и «l2». |
Фильтры карманные и кассетные
Появилась возможность рассчитывать фильтры как в сборе, так и отдельно: по корпусу и фильтровальному элементу, а также возможность различной укладки фильтровальной кассеты
Расчет фасонных элементов для систем аспирации и пневмотранспорта
Тройники и крестовина аспирационные
Тройник круглого сечения аспирационный |
Тройник круглого сечения аспирационный штаны |
Крестовина круглого сечения аспирационная |
Реализован расчет
Отводы и полу-отводы круглого сечения с различным радиусом изгиба и углом поворота, а так же
с изменяемым сечением можно найти в группе отводов. |
Учет замков в расчете продукции
На всех группах продукции при расчете площади продукции появилась возможность учитывать припуски на замки (от одного до четырех)
Используется один замок |
Используются два замка |
Используется три замка |
Используется четыре замка |
В рамках данного релиза будет реализована валидация данных.
Расширенные настройки параметров продукции
На всей продукции появилась возможность редактировать припуски на соединения!
Отводы |
Переходы |
Крестовины |
Тройники |
Расчет массы и объема продукции
С вводом функции учета замков появилась возможность рассчитывать точный вес готовой продукции, что в свою
очередь позволяет определить грузоподъемность транспорта для перевозки готовой продукции (заказа).
Расет объема продукции так же важен при определении вида и типа грузоперевозчика.
Грузоподъемность — 1,5тОбъем кузова — 10 м3 |
Грузоподъемность — 3,5тОбъем кузова — 25 м3 |
Грузоподъемность — 20тОбъем кузова — 100 м3 |
А что же дальше?
Запущен в разработку механизм валидации (корректного ввода исходных данных), что исключает ошибку как менеджера, обрабатывающего заявку, так и проектировщика, допустившего описку.
При l/2 |
При d/2>A |
При l/vr>=L |
При введении недопустимых параметров программа будет уведомлять пользователя о введении некорректных данных.
Актуальный релиз всегда можно скачать в Личном кабинете
С уважением, компания «СофтВент»
e-mail: [email protected]
тел. +7(916) 106-05-50 Отдел методологии
тел. +7(915) 116-73-21 Отдел техподдержки 1С
Методика аэродинамического расчета воздуховодов — Мир Климата и Холода
Этим материалом редакция журнала «МИР КЛИМАТА» продолжает публикацию глав из книги «Системы вентиляции и кондиционирования. Рекомендации по проектированию для произ-
водственных и общественных зданий». Автор Краснов Ю.С.
Аэродинамический расчет воздуховодов начинают с вычерчивания аксонометрической схемы (М 1: 100), проставления номеров участков, их нагрузок L (м3/ч) и длин I (м). Определяют направление аэродинамического расчета – от наиболее удаленного и нагруженного участка до вентилятора. При сомнениях при определении направления рассчитывают все возможные варианты.
Расчет начинают с удаленного участка: определяют диаметр D (м) круглого или площадь F (м2) поперечного сечения прямоугольного воздуховода:
Рекомендуемую скорость принимают следующей:
| в начале системы | вблизи вентилятора | |
| Административные здания | 4…5 м/с | 8…12 м/с |
| Производственные здания | 5…6 м/с | 10/…16 м/с |
Скорость растет по мере приближения к вентилятору.
По приложению Н из [30] принимают ближайшие стандартные значения: DCT или (а х b)ст (м).
| Рис. 1. Аксонометрическая схема воздуховода |
Фактическая скорость (м/с):
| или |
Гидравлический радиус прямоугольных воздуховодов (м):
| Критерий Рейнольдса: Re=64100×Dст× υфакт (для прямоугольных воздуховодов Dст=DL). Коэффициент гидравлического трения: λ=0,3164⁄Re-0,25 при Re≤60000, λ=0,1266⁄Re-0,167 при Re>60000. Потери давления на расчетном участке (Па): |
где – сумма коэффициентов местных сопротивлений на участке воздуховодов.
Местные сопротивления на границе двух участков (тройники, крестовины) относят к участку с меньшим расходом.
Коэффициенты местных сопротивлений даны в приложениях.
Схема приточной системы вентиляции, обслуживающей 3-этажное административное здание
Пример расчета
Исходные данные:
| № участков | подача L, м3/ч | длина L, м | υрек, м/с | сечение а × b, м | υф, м/с | Dl,м | Re | λ | Kmc | потери на участке Δр, па |
| решетка рр на выходе | 0,2 × 0,4 | 3,1 | — | — | — | 1,8 | 10,4 | |||
| 1 | 720 | 4,2 | 4 | 0,2 × 0,25 | 4,0 | 0,222 | 56900 | 0,0205 | 0,48 | 8,4 |
| 2 | 1030 | 3,0 | 5 | 0,25× 0,25 | 4,6 | 0,25 | 73700 | 0,0195 | 0,4 | 8,1 |
| 3 | 2130 | 2,7 | 6 | 0,4 × 0,25 | 5,92 | 0,308 | 116900 | 0,0180 | 0,48 | 13,4 |
| 4 | 3480 | 14,8 | 7 | 0,4 × 0,4 | 6,04 | 0,40 | 154900 | 0,0172 | 1,44 | 45,5 |
| 5 | 6830 | 1,2 | 8 | 0,5 × 0,5 | 7,6 | 0,50 | 234000 | 0,0159 | 0,2 | 8,3 |
| 6 | 10420 | 6,4 | 10 | 0,6 × 0,5 | 9,65 | 0,545 | 337000 | 0,0151 | 0,64 | 45,7 |
| 6а | 10420 | 0,8 | ю. | Ø0,64 | 8,99 | 0,64 | 369000 | 0,0149 | 0 | 0,9 |
| 7 | 10420 | 3,2 | 5 | 0,53 × 1,06 | 5,15 | 0,707 | 234000 | 0,0312 ×n | 2,5 | 44,2 |
| Суммарные потери: 185 | ||||||||||
| Таблица 1. Аэродинамический расчет | ||||||||||
| Примечание. Для кирпичных каналов с абсолютной шероховатостью 4 мм и υф = 6,15 м/с, поправочный коэффициент n = 1,94 ([32], табл. 22.12.) |
Воздуховоды изготовлены из оцинкованной тонколистовой стали, толщина и размер которой соответствуют прил. Н из [30]. Материал воздухозаборной шахты – кирпич. В качестве воздухораспределителей применены решетки регулируемые типа РР с возможными сечениями: 100 х 200; 200 х 200; 400 х 200 и 600 х 200 мм, коэффициентом затенения 0,8 и максимальной скоростью воздуха на выходе до 3 м/с.
Сопротивление приемного утепленного клапана с полностью открытыми лопастями 10 Па. Гидравлическое сопротивление калориферной установки 100 Па (по отдельному расчету). Сопротивление фильтра G-4 250 Па. Гидравлическое сопротивление глушителя 36 Па (по акустическому расчету). Исходя из архитектурных требований проектируют воздуховоды прямоугольного сечения.
Сечения кирпичных каналов принимают по табл. 22.7 [32].
Коэффициенты местных сопротивлений
Участок 1. Решетка РР на выходе сечением 200×400 мм (рассчитывают отдельно):
Динамическое давление:
| KMC решетки (прил. 25.1) = 1,8. Падение давления в решетке: Δр – рД × KMC = 5,8 × 1,8 = 10,4 Па. Расчетное давление вентилятора р: Δрвент = 1,1 (Δраэрод + Δрклап + Δрфильтр + Δркал + Δрглуш)= 1,1 (185 + 10 + 250 + 100 + 36) = 639 Па. Подача вентилятора: Lвент= 1,1 х Lсист = 1,1 х 10420 = 11460 м3/ч. Выбран радиальный вентилятор ВЦ4-75 № 6,3, исполнение 1: L = 11500 м3/ч; Δрвен = 640 Па (вентагрегат Е6.3.090- 2а), диаметр ротора 0,9 х Dпом., частота вращения 1435 мин-1, электродвигатель 4А10054; N = 3 кВт установлен на одной оси с вентилятором. Масса агрегата 176 кг. Проверка мощности электродвигателя вентилятора (кВт): |
По аэродинамической характеристике вентилятора nвент = 0,75.
| № участков | Вид местного сопротивления | Эскиз | Угол α, град. | Отношение | Обоснование | КМС | ||
| F0/F1 | L0/Lст | fпрох/fств | ||||||
| 1 | Диффузор | 20 | 0,62 | | Табл. |  25.1 25.10,09 | | ||
| Отвод | 90 | | — | Табл. 25.11 | 0,19 | | |||
| Тройник-проход | | 0,3 | 0,8 | Прил. 25.8 | 0,2 | | |||
| ∑ = | 0,48 | |||||||
| 2 | Тройник-проход | | 0,48 | 0,63 | Прил. 25.8 | 0,4 | | ||
| 3 | Тройник-ответвление | | 0,63 | 0,61 | Прил. 25.9 | 0,48 | | ||
| 4 | 2 отвода | 250 × 400 | 90 | | — | Прил. 25.11 | | | |
| Отвод | 400 × 250 | 90 | | — | Прил. 25.11 | 0,22 | | ||
| Тройник-проход | | 0,49 | 0,64 | Табл. |  25.8 25.80,4 | | |||
| ∑ = | 1,44 | |||||||
| 5 | Тройник-проход | | 0,34 | 0,83 | Прил. 25.8 | 0,2 | | ||
| 6 | Диффузор после вентилятора | h=0,6 | 1,53 | | Прил. 25.13 | 0,14 | | ||
| Отвод | 600 × 500 | 90 | | — | Прил. 25.11 | 0,5 | | ||
| ∑= | 0,64 | |||||||
| 6а | Конфузор перед вентилятором | Dг=0,42 м | Табл. 25.12 | 0 | ||||
| 7 | Колено | 90 | | — | Табл. 25.1 | 1,2 | | ||
| Решетка жалюзийная | Табл. 25.1 25.1 | 1,3 | ||||||
| ∑ = | 1,44 | |||||||
| Таблица 2. Определение местных сопротивлений | ||||||||
Краснов Ю.С.,
“Системы вентиляции и кондиционирования. Рекомендации по проектированию для производственных и общественных зданий”, глава 15. “Термокул”
Определение коэффициентов местных сопротивлений тройников в системах вентиляции | C.O.K. archive
Цель аэродинамического расчета заключается в определении размеров поперечных сечений и потерь давлений на участках системы и в системе в целом. При расчете необходимо учитывать следующие положения.
1. На аксонометрической схеме системы проставляются расходы и двсех участков.
2. Выбирается магистральное направление и производится нумерация участков, затем нумеруют ответвления.
3. По допустимой скорости на участках магистрального направления определяют площади поперечных сечений:
Полученный результат округляют до стандартных значений, являющихся расчетными, и по стандартной площади находят диаметр d или размеры a и b канала.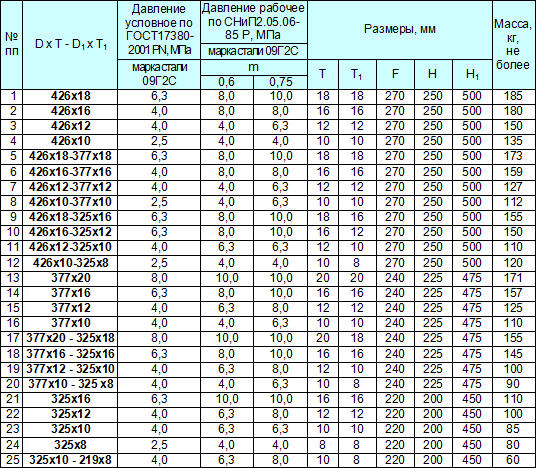
В справочной литературе до таблиц аэродинамического расчета приведен перечень стандартных размеров площадей воздуховодов круглой и прямоугольной формы.
*Примечание: мелкие птицы, попавшие в зону факела со скоростью, равной 8 м/с, прилипают к решетке.
4. Из таблиц аэродинамического расчета по выбранному диаметру и расходу на участке определяют расчетные значения скорости υ, удельные потери на трение R, динамическое давление Р дин. Если необходимо, то определяют коэффициент относительной шероховатости β ш.
5. На участке определяют виды местных сопротивлений, их коэффициенты ξ и суммарное значение ∑ξ.
6. Находят потери давления в местных сопротивлениях:
Z = ∑ξ · Р дин.
7. Определяют потери давления на трение:
∆Р тр = R · l.
8.Рассчитывают потери давления на данном участке по одной из следующих формул:
∆Р уч = Rl + Z,
∆Р уч = Rlβ ш + Z.
Расчет повторяют с пункта 3 до пункта 8 для всех участков магистрального направления.
9. Определяют потери давления в оборудовании, расположенном на магистральном направлении ∆Р об.
10. Рассчитывают сопротивление системы ∆Р с.
11. Для всех ответвлений повторяют расчет с пункта 3 до пункта 9, если на ответвлениях есть оборудование.
12. Производят увязку ответвлений с параллельными участками магистрали:
. (178)
Ответвления должны иметь сопротивление немного больше или равное сопротивлению параллельного участка магистрали.
Воздуховоды прямоугольной формы имеют аналогичный порядок расчета, только в пункте 4 по значению скорости, найденной из выражения:
,
и эквивалентного диаметра по скорости d υ находят из таблиц аэродинамического расчета справочной литературы удельные потери на трение R, динамическое давление Р дин, причем L табл ≠ L уч.
Аэродинамические расчеты обеспечивают выполнение условия (178) за счет изменения диаметров на ответвлениях или установкой дросселирующих устройств (дроссель-клапанов, шиберов).
Для некоторых местных сопротивлений значение ξ приводится в справочной литературе в зависимости от скорости.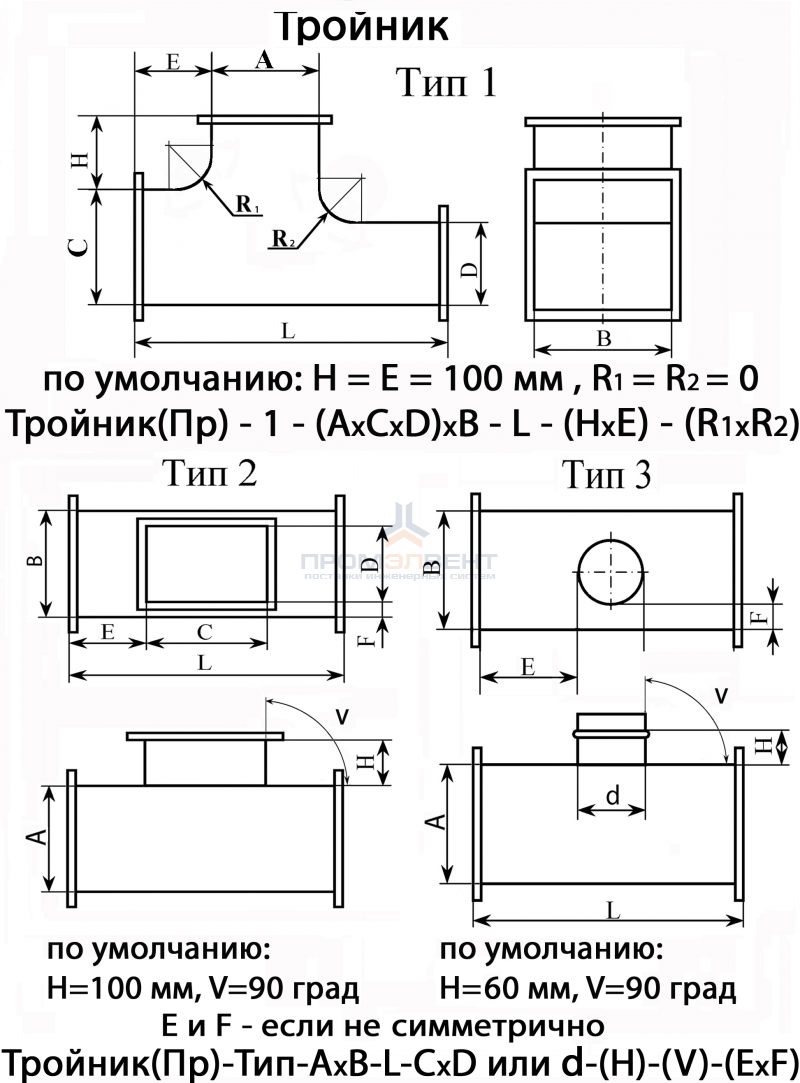 Если значение расчетной скорости не совпадает с табличным, то ξ пересчитывают по выражению:
Если значение расчетной скорости не совпадает с табличным, то ξ пересчитывают по выражению:
Для неразветвленных систем или систем незначительных размеров увязку ответвлений производят не только с помощью дроссель-клапанов, но и диафрагм.
Для удобства аэродинамический расчет выполняют в табличной форме.
Рассмотрим порядок аэродинамического расчета вытяжной механической системы вентиляции.
| №№ участ-ка | L, м 3 /ч | F, м 2 | V, м/с | a×b, мм | D э, мм | β ш | R, Па/м | l, м | Rlβ ш, Па | Вид местного сопротивления | ∑ξ | Р д, Па | Z=∑ξ· Р д Па | ΔР = Rl + Z, Па |
| на участке | на магист-рале | |||||||||||||
| 1-2 | 0,196 | 11,71 | — | 2,56 | 11,93 | 30,5 | 0,42-вн. расширение 0,38-конфузор 0,21-2отвода 0,35-тройник | 1,57 | 83,63 | 131,31 | 282,85 | 282,85 | ||
| 2-3 | 0,396 | 11,59 | — | 1,63 | 15,35 | 25,0 | 0,21-3отвода 0,2-тройник | 0,83 | 81,95 | 68,02 | 93,04 | 375,89 | ||
| 3-4 | 0,502 | 10,93 | — | 1,25 | 2,76 | 3,5 | 0,21-2отвода 0,1-переход | 0,52 | 72,84 | 37,88 | 41,33 | 417,21 | ||
| 4-5 | 0,632 | 8,68 | 795х795 | 2,085 | 0,82 | 3,50 | 6,0 | 5,98 | 423,20 | |||||
| 2″-2 | 0,196 | 11,71 | — | 2,56 | 6,27 | 16,1 | 0,42-вн. расширение 0,38-конфузор 0,21-2отвода 0,98-тройник расширение 0,38-конфузор 0,21-2отвода 0,98-тройник | 1,99 | 83,63 | 166,43 | 303,48 | |||
| 6-7 | 0,0375 | 5,50 | 250х200 | — | 1,8-сетка | 1,80 | 18,48 | 33,26 | 33,26 | |||||
| 0,078 | 10,58 | — | 3,79 | 5,54 | 21,0 | 1,2-поворот 0,17-тройник | 1,37 | 68,33 | 93,62 | 114,61 | ||||
| 7-3 | 0,078 | 11,48 | — | 4,42 | 5,41 | 23,9 | 0,17-отвод 1,35-тройник | 1,52 | 80,41 | 122,23 | 146,14 | |||
| 7″-7 | 0,015 | 4,67 | 200х100 | — | 1,8-сетка | 1,80 | 13,28 | 23,91 | 23,91 | |||||
| 0,0123 | 5,69 | — | 3,80 | 1,23 | 4,7 | 1,2-поворот 5,5-тройник | 6,70 | 19,76 | 132,37 | 137,04 |
Тройники имеют два сопротивления — на проход и на ответвление, и они всегда относятся к участкам с меньшим расходом, т. е. либо к проходному сечению, либо к ответвлению. При расчете ответвлений в графе 16 (табл. стр.88) прочерк.
е. либо к проходному сечению, либо к ответвлению. При расчете ответвлений в графе 16 (табл. стр.88) прочерк.
Главное требование ко всем типам систем вентиляции – обеспечивать оптимальную кратность обмена воздуха в помещениях или конкретных рабочих зонах. С учетом этого параметра проектируется внутренний диаметр воздуховода и подбирается мощность вентилятора. Для того чтобы гарантировать требуемую эффективность функционирования системы вентиляции, выполняется расчет потерь давления напора в воздуховодах, эти данные принимаются во внимание во время определения технических характеристик вентиляторов. Показатели рекомендуемой скорости воздушного потока указаны в таблице № 1.
Табл. № 1. Рекомендованная скорость движения воздуха для различных помещений
| Назначение | Основное требование | ||||
| Бесшумность | Мин. потери напора | ||||
| Магистральные каналы | Главные каналы | Ответвления | |||
| Приток | Вытяжка | Приток | Вытяжка | ||
| Жилые помещения | 3 | 5 | 4 | 3 | 3 |
| Гостиницы | 5 | 7. 5 5 | 6.5 | 6 | 5 |
| Учреждения | 6 | 8 | 6.5 | 6 | 5 |
| Рестораны | 7 | 9 | 7 | 7 | 6 |
| Магазины | 8 | 9 | 7 | 7 | 6 |
Исходя из этих значений следует рассчитывать линейные параметры воздуховодов.
Алгоритм расчета потерь напора воздуха
Расчет нужно начинать с составления схемы системы вентиляции с обязательным указанием пространственного расположения воздуховодов, длины каждого участка, вентиляционных решеток, дополнительного оборудования для очистки воздуха, технической арматуры и вентиляторов. Потери определяются вначале по каждой отдельной линии, а потом суммируются. По отдельному технологическому участку потери определяются с помощью формулы P = L×R+Z, где P – потери воздушного давления на расчетном участке, R – потери на погонном метре участка, L – общая длина воздуховодов на участке, Z – потери в дополнительной арматуре системы вентиляции.
Для расчета потерь давления в круглом воздуховоде используется формула Pтр. = (L/d×X) × (Y×V)/2g. X – табличный коэффициент трения воздуха, зависит от материала изготовления воздуховода, L – длина расчетного участка, d – диаметр воздуховода, V – требуемая скорость воздушного потока, Y – плотность воздуха с учетом температуры, g – ускорение падения (свободного). Если система вентиляции имеет квадратные воздуховоды, то для перевода круглых значений в квадратные следует пользоваться таблицей № 2.
Табл. № 2. Эквивалентные диаметры круглых воздуховодов для квадратных
| 150 | 200 | 250 | 300 | 350 | 400 | 450 | 500 | |
| 250 | 210 | 245 | 275 | |||||
| 300 | 230 | 265 | 300 | 330 | ||||
| 350 | 245 | 285 | 325 | 355 | 380 | |||
| 400 | 260 | 305 | 345 | 370 | 410 | 440 | ||
| 450 | 275 | 320 | 365 | 400 | 435 | 465 | 490 | |
| 500 | 290 | 340 | 380 | 425 | 455 | 490 | 520 | 545 |
| 550 | 300 | 350 | 400 | 440 | 475 | 515 | 545 | 575 |
| 600 | 310 | 365 | 415 | 460 | 495 | 535 | 565 | 600 |
| 650 | 320 | 380 | 430 | 475 | 515 | 555 | 590 | 625 |
| 700 | 390 | 445 | 490 | 535 | 575 | 610 | 645 | |
| 750 | 400 | 455 | 505 | 550 | 590 | 630 | 665 | |
| 800 | 415 | 470 | 520 | 565 | 610 | 650 | 685 | |
| 850 | 480 | 535 | 580 | 625 | 670 | 710 | ||
| 900 | 495 | 550 | 600 | 645 | 685 | 725 | ||
| 950 | 505 | 560 | 615 | 660 | 705 | 745 | ||
| 1000 | 520 | 575 | 625 | 675 | 720 | 760 | ||
| 1200 | 620 | 680 | 730 | 780 | 830 | |||
| 1400 | 725 | 780 | 835 | 880 | ||||
| 1600 | 830 | 885 | 940 | |||||
| 1800 | 870 | 935 | 990 |
По горизонтали указана высота квадратного воздуховода, а по вертикали ширина.
Эквивалентное значение круглого сечения находится на пересечении линий.
Потери давления воздуха в изгибах берутся из таблицы № 3.
Табл. № 3. Потери давления на изгибах
Для определения потерь давления в диффузорах используются данные из таблицы № 4.
Табл. № 4. Потери давления в диффузорах
В таблице № 5 дается общая диаграмма потерь на прямолинейном участке.
Табл. № 5. Диаграмма потерь давления воздуха в прямолинейных воздуховодах
Все отдельные потери на данном участке воздуховода суммируются и корректируются с таблицей № 6. Табл. № 6. Расчет понижения давления потока в системах вентиляции
Во время проектирования и расчетов существующие нормативные акты рекомендуют, чтобы разница в величине потерь давления между отдельными участками не превышала 10%. Вентилятор нужно устанавливать в участке системы вентиляции с наиболее высоким сопротивлением, самые удаленные воздуховоды должны иметь минимальное сопротивление. Если эти условия не выполняются, то необходимо изменять план размещения воздуховодов и дополнительного оборудования с учетом требований положений.
Если эти условия не выполняются, то необходимо изменять план размещения воздуховодов и дополнительного оборудования с учетом требований положений.
Чтобы определиться с размерами сечений на любом из отрезков воздухораспределительной системы, необходимо произвести аэродинамический расчет воздуховодов. Показатели, полученные при таком расчёте, определяют работоспособность как всей проектируемой системы вентиляции, так и отдельных её участков.
Для создания комфортных условий в кухне, отдельной комнате или помещении в целом необходимо обеспечить правильную проектировку воздухораспределительной системы, которая состоит из множества деталей. Важное место среди них занимает воздуховод, определение квадратуры которого оказывает влияние на значение скорости воздушного потока и шумность вентиляционной системы в целом. Определить эти и ряд других показателей позволит аэродинамический расчет воздуховодов.
Расчет потерь давления в воздуховоде
Когда известны параметры воздуховодов (их длина, сечение, коэффициент трения воздуха о поверхность), можно рассчитать потери давления в системе при проектируемом расходе воздуха.
Общие потери давления (в кг/кв.м.) рассчитываются по формуле:
P = R*l + z,
где R — потери давления на трение в расчете на 1 погонный метр воздуховода, l — длина воздуховода в метрах, z — потери давления на местные сопротивления (при переменном сечении).
1. Потери на трение:
В круглом воздуховоде потери давления на трение Pтр считаются так:
Pтр = (x*l/d) * (v*v*y)/2g,
где x — коэффициент сопротивления трения, l — длина воздуховода в метрах, d — диаметр воздуховода в метрах, v — скорость течения воздуха в м/с, y — плотность воздуха в кг/куб.м., g — ускорение свободного падения (9,8 м/с2).
- Замечание: Если воздуховод имеет не круглое, а прямоугольное сечение, в формулу надо подставлять эквивалентный диаметр, который для воздуховода со сторонами А и В равен: dэкв = 2АВ/(А + В)
2. Потери на местные сопротивления:
Потери на местные сопротивления:
Потери давления на местные сопротивления считаются по формуле:
z = Q* (v*v*y)/2g,
где Q — сумма коэффициентов местных сопротивлений на участке воздуховода, для которого производят расчет, v — скорость течения воздуха в м/с, y — плотность воздуха в кг/куб.м., g — ускорение свободного падения (9,8 м/с2). Значения Q содержатся в табличном виде.
Этап первый
Сюда входит аэродинамический расчёт механических систем кондиционирования или вентиляции, который включает ряд последовательных операций.Составляется схема в аксонометрии, которая включает вентиляцию: как приточную, так и вытяжную, и подготавливается к расчёту.
Размеры площади сечений воздуховодов определяются в зависимости от их типа: круглого или прямоугольного.
Формирование схемы
Схема составляется в аксонометрии с масштабом 1:100. На ней указываются пункты с расположенными вентиляционными устройствами и потреблением воздуха, проходящего через них.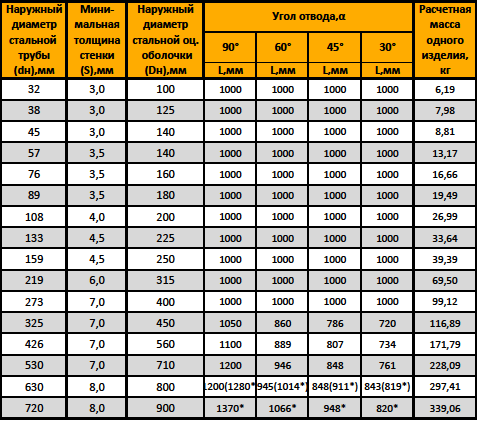
Здесь следует определиться с магистралью – основной линией исходя из которой проводятся все операции. Она представляет собой цепь последовательно соединённых отрезков, с наибольшей нагрузкой и максимальной протяжённостью.
Выстраивая магистраль, следует обратить внимание на то какая система проектируется: приточная или вытяжная.
Приточная
Здесь линия расчёта выстраивается от самого удалённого распределителя воздуха с наибольшим потреблением. Она проходит через такие приточные элементы, как воздуховоды и вентиляционная установка вплоть до места где происходит забор воздуха. Если же система должна обслуживать несколько этажей, то распределитель воздуха располагают на последнем.
Вытяжная
Строится линия от самого удалённого вытяжного устройства, максимально расходующего воздушный поток, через магистраль до установки вытяжки и дальше до шахты, через которую осуществляется выброс воздуха.
Если планируется вентиляция для нескольких уровней и установка вытяжки располагается на кровле или чердаке, то линия расчёта должна начинаться с воздухораспределительного устройства самого нижнего этажа или подвала, который тоже входит в систему. Если установка вытяжки находится в подвальном помещении, то от воздухораспределительного устройства последнего этажа.
Если установка вытяжки находится в подвальном помещении, то от воздухораспределительного устройства последнего этажа.
Вся линия расчёта разбивается на отрезки, каждый из них представляет собой участок воздуховода со следующими характеристиками:
- воздуховод единого размера сечения;
- из одного материала;
- с постоянным потреблением воздуха.
Следующим шагом является нумерация отрезков. Начинается она с наиболее удалённого вытяжного устройства или распределителя воздуха, каждому присваивается отдельный номер. Основное направление – магистраль выделяется жирной линией.
Далее, на основе аксонометрической схемы для каждого отрезка определяется его протяжённость с учётом масштаба и потребления воздуха. Последний представляет собой сумму всех величин потребляемого воздушного потока, протекающего через ответвления, которые примыкают к магистрали. Значение показателя, который получается в результате последовательного суммирования, должно постепенно возрастать.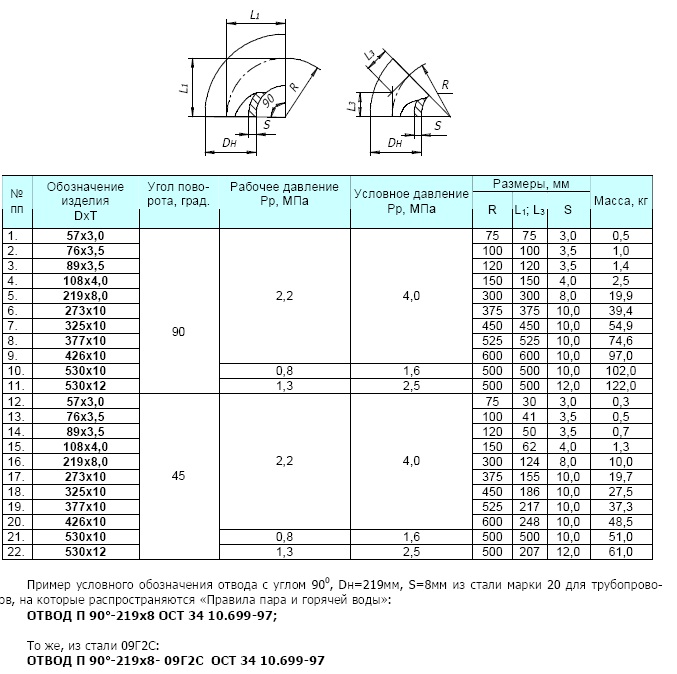
Определение размерных величин сечений воздуховодов
Производится исходя из таких показателей, как:
- потребление воздуха на отрезке;
- нормативные рекомендуемые значения скорости движения воздушного потока составляют: на магистралях — 6м/с, на шахтах где происходит забор воздуха – 5м/с.
Рассчитывается предварительное размерная величина воздуховода на отрезке, которая приводится к ближайшему стандартному. Если выбирается прямоугольный воздуховод, то значения подбираются на основе размеров сторон, отношение между которыми составляет не более чем 1 к 3.
Аэродинамический расчет воздуховодов – алгоритм действий
Работы включают в себя несколько последовательных этапов, каждый из которых решает локальные задачи. Полученные данные форматируются в виде таблиц, на их основании составляются принципиальные схемы и графики. Работы разделяются на следующие этапы:
- Разработка аксонометрической схемы распределения воздуха по системе. На основе схемы определяется конкретная методика расчетов с учетом особенностей и задач вентиляционной системы.
- Выполняется аэродинамический расчет воздуховодов как по главным магистралям, так и по всем ответвлениям.
- На основании полученных данных выбирается геометрическая форма и площадь сечения воздуховодов, определяются технические параметры вентиляторов и калориферов. Дополнительно принимается во внимание возможность установки датчиков пожаротушения, предупреждения распространения дыма, возможность автоматической регулировки мощности вентиляции с учетом составленной пользователями программы.
Этап второй
Здесь рассчитываются аэродинамические показатели сопротивления. После выбора стандартных сечений воздуховодов уточняется величина скорости воздушного потока в системе.
Расчёт потерь давления на трение
Следующим шагом является определение удельных потерь давления на трение исходя из табличных данных или номограмм. В ряде случаев может пригодиться калькулятор для определения показателей на основе формулы, позволяющей произвести расчёт с погрешностью в 0,5 процента. Для вычисления общего значения показателя, характеризующего потери давления на всём участке, нужно его удельный показатель умножить на длину. На этом этапе также следует учитывать поправочный коэффициент на шероховатость. Он зависит от величины абсолютной шероховатости того или иного материала воздуховода, а также скорости.
Для вычисления общего значения показателя, характеризующего потери давления на всём участке, нужно его удельный показатель умножить на длину. На этом этапе также следует учитывать поправочный коэффициент на шероховатость. Он зависит от величины абсолютной шероховатости того или иного материала воздуховода, а также скорости.
Вычисление показателя динамического давления на отрезке
Здесь определяют показатель, характеризующий динамическое давление на каждом участке исходя из значений:
- скорости воздушного потока в системе;
- плотности воздушной массы в стандартных условиях, которая составляет 1,2 кг/м3.
Определение значений местных сопротивлений на участках
Их можно рассчитать исходя из коэффициентов местного сопротивления. Полученные значения сводят в табличной форме, в которую включаются данные всех участков, причём не только прямые отрезки, но и по несколько фасонных частей. Название каждого элемента заносится в таблицу, там же указываются соответствующие значения и характеристики, по которым определяется коэффициент местного сопротивления. Эти показатели можно найти в соответствующих справочных материалах по подбору оборудования для вентиляционных установок.
Эти показатели можно найти в соответствующих справочных материалах по подбору оборудования для вентиляционных установок.
При наличии большого количества элементов в системе или при отсутствии определённых значений коэффициентов используется программа, которая позволяет быстро осуществить громоздкие операции и оптимизировать расчёт в целом. Общая величина сопротивления определяется как сумма коэффициентов всех элементов отрезка.
Вычисление потерь давления на местных сопротивлениях
Рассчитав итоговую суммарную величину показателя, переходят к вычислению потерь давления на анализируемых участках. После расчёта всех отрезков основной линии полученные числа суммируют и определяют общее значение сопротивления вентиляционной системы.
Бланк расчета системы вентиляции
№ участка (см. рис. 2.2)
P
Д,
Па
Значения R
определяют или по специальным таблицам, или по номограмме (рисунок 3.2), составленной для стальных круглых воздуховодов диаметром
d
. Этой же номограммой можно пользоваться и для расчета воздуховодов прямоугольного сечения
ab
, только в этом случае под величиной
d
понимают эквивалентный диаметр
d
э = 2
ab
/(
a
+
b
). На номограмме указаны также значения динамического давления потока воздуха, соответствующие плотности стандартного воздуха (
t
= 20 о C; φ = 50 %; барометрическое давление 101,3 кПа;
= 1,2 кг/м 3 ). При плотности
динамическое давление равно показанию шкалы, умноженному на отношение
/1,2
Подбирают вентиляторы по аэродинамическим характеристикам, показывающим графическую взаимозависимость их полного давления, подачи, частоты вращения и окружной скорости рабочего колеса. Эти характеристики составлены для стандартного воздуха.
Удобно вести подбор вентиляторов по номограммам, представляющим собой сводные характеристики вентиляторов одной серии. На рисунке 3. 3 изображена номограмма для выбора центробежных вентиляторов серии Ц4-70 * , получивших широкое применение в вентиляционных системах сельскохозяйственных производственных зданий и сооружений. Эти вентиляторы обладают высокими аэродинамическими качествами, бесшумны в работе.
3 изображена номограмма для выбора центробежных вентиляторов серии Ц4-70 * , получивших широкое применение в вентиляционных системах сельскохозяйственных производственных зданий и сооружений. Эти вентиляторы обладают высокими аэродинамическими качествами, бесшумны в работе.
Из точки, соответствующей найденному значению подачи L
в, проводят прямую до пересечения с лучом номера вентилятора (№ вент.) и далее по вертикали до линии расчетного полного давления
вентилятора.
Точка пересечения соответствует КПД вентилятора
и значению безразмерного коэффициентаА
, по которому подсчитывают частоту вращения вентилятора (мин -1 ).
Горизонтальная шкала номограммы показывает скорость движения воздуха в выпускном отверстии вентилятора.
Подбор вентилятора надо вести с таким расчетом, чтобы его КПД был не ниже 0,85 максимального значения.
Необходимая мощность на валу электродвигателя для привода вентилятора, кВт:
Рис. 3.2 Номограмма для расчетов круглых стальных воздуховодов
3.2 Номограмма для расчетов круглых стальных воздуховодов
Рис.3.3 Номограмма для подбора центробежных вентиляторов серии Ц4-70
Этап третий: увязка ответвлений
Когда проведены все необходимые расчёты необходимо произвести увязку нескольких ответвлений. Если система обслуживает один уровень, то увязывают ответвления не входящие в магистраль. Расчёт проводят в том же порядке, что и для основной линии. Результаты заносятся в таблицу. В многоэтажных зданиях для увязки используются поэтажные ответвления на промежуточных уровнях.
Критерии увязки
Здесь сопоставляются значения суммы потерь: давления по увязываемым отрезкам с параллельно присоединённой магистралью. Необходимо чтобы отклонение составляло не более 10 процентов. Если установлено, что расхождение больше, то увязку можно проводить:
- путём подбора соответствующих размеров сечения воздуховодов;
- при помощи установки на ответвлениях диафрагм или дроссельных клапанов.
Иногда для проведения подобных расчётов необходим всего лишь калькулятор и пара справочников. Если же требуется провести аэродинамический расчёт вентиляции больших зданий или производственных помещений, то понадобится соответствующая программа. Она позволит быстро определить размеры сечений, потери давления как на отдельных отрезках, так и во всей системе в целом.
Если же требуется провести аэродинамический расчёт вентиляции больших зданий или производственных помещений, то понадобится соответствующая программа. Она позволит быстро определить размеры сечений, потери давления как на отдельных отрезках, так и во всей системе в целом.
https://www.youtube.com/watch?v=v6stIpWGDow Video can’t be loaded: Проектирование систем вентиляции. (https://www.youtube.com/watch?v=v6stIpWGDow)
Целью аэродинамического расчета является определение потерь давления (сопротивления) движению воздуха во всех элементах системы вентиляции — воздуховодах, их фасонных элементах, решетках, диффузорах, воздухонагревателях и других. Зная общую величину этих потерь, можно подобрать вентилятор, способный обеспечить необходимый расход воздуха. Различают прямую и обратную задачи аэродинамического расчета. Прямая задача решается при проектировании вновь создаваемых систем вентиляции, состоит в определении площади сечения всех участков системы при заданном расходе через них. Обратная задача – определение расхода воздуха при заданной площади сечения эксплуатируемых или реконструируемых систем вентиляции. В таких случаях для достижения требуемого расхода достаточно изменения частоты вращения вентилятора или его замены на другой типоразмер.
Аэродинамический расчет начинают после определения кратности воздухообмена помещений и принятия решения по трассировке (схеме прокладки) воздуховодов и каналов. Кратность воздухообмена является количественной характеристикой работы системы вентиляции, показывает, сколько раз в течение 1-го часа объем воздуха помещения полностью заменится новым. Кратность зависит от характеристик помещения, его назначения и может отличаться в несколько раз. Перед началом аэродинамического расчета создается схема системы в аксонометрической проекции и масштабе М 1:100. На схеме выделяют основные элементы системы: воздуховоды, их фасонные части, фильтры, шумоглушители, клапана, воздухонагреватели, вентиляторы, решетки и другие. По этой схеме, строительным планам помещений определяют длину отдельных ветвей. Схему делят на расчетные участки, которые имеют постоянный расход воздуха. Границами расчетных участков являются фасонные элементы – отводы, тройники и прочие. Определяют расход на каждом участке, наносят его, длину, номер участка на схему. Далее выбирают магистраль – наиболее длинную цепь последовательно расположенных участков, считая от начала системы до самого удаленного ответвления. Если в системе несколько магистралей одинаковой длины, то главной выбирают с большим расходом. Принимается форма поперечного сечения воздуховодов – круглая, прямоугольная или квадратная. Потери давления на участках зависят от скорости воздуха и состоят из: потерь на трение и в местных сопротивлениях. Общие потери давления системы вентиляции равны потерям магистрали и состоят из суммы потерь всех ее расчетных участков. Выбирают направление расчета – от самого дальнего участка до вентилятора.
Схему делят на расчетные участки, которые имеют постоянный расход воздуха. Границами расчетных участков являются фасонные элементы – отводы, тройники и прочие. Определяют расход на каждом участке, наносят его, длину, номер участка на схему. Далее выбирают магистраль – наиболее длинную цепь последовательно расположенных участков, считая от начала системы до самого удаленного ответвления. Если в системе несколько магистралей одинаковой длины, то главной выбирают с большим расходом. Принимается форма поперечного сечения воздуховодов – круглая, прямоугольная или квадратная. Потери давления на участках зависят от скорости воздуха и состоят из: потерь на трение и в местных сопротивлениях. Общие потери давления системы вентиляции равны потерям магистрали и состоят из суммы потерь всех ее расчетных участков. Выбирают направление расчета – от самого дальнего участка до вентилятора.
По площади F
определяют диаметр
D
(для круглой формы) или высоту
A
и ширину
B
(для прямоугольной) воздуховода, м. Полученные величины округляют до ближайшего большего стандартного размера, т.е.
Полученные величины округляют до ближайшего большего стандартного размера, т.е.
D ст
,
А ст
и
В ст
(справочная величина).
Пересчитывают фактические площадь сечения F
факт и скорость
v факт
.
Для прямоугольного воздуховода определяют т.н. эквивалентный диаметр DL = (2A ст * B ст ) / (A
ст+ Bст), м.
Определяют величину критерия подобия Рейнольдса Re = 64100* D
ст* v факт.
Для прямоугольной формы
D L = D ст .
Коэффициент трения λ тр = 0,3164 ⁄ Re-0,25 при Re≤60000, λ
тр= 0,1266 ⁄ Re-0,167 при Re>60000.
Коэффициент местного сопротивления λм
зависит от их типа, количества и выбирается из справочников.
Комментариев:
- Исходные данные для вычислений
- С чего начинать? Порядок вычислений
Сердцем любой вентиляционной системы с механическим побуждением воздушного потока является вентилятор, который создает этот поток в воздуховодах. Мощность вентилятора напрямую зависит от напора, который необходимо создать на выходе из него, а для того, чтобы определить величину этого давления, требуется произвести расчет сопротивления всей системы каналов.
Мощность вентилятора напрямую зависит от напора, который необходимо создать на выходе из него, а для того, чтобы определить величину этого давления, требуется произвести расчет сопротивления всей системы каналов.
Для расчета потерь давления нужна схема и размеры воздуховода и дополнительного оборудования.
Основные формулы аэродинамического расчета
Первым делом необходимо сделать аэродинамический расчет магистрали. Напомним что магистральным воздуховодом считается наиболее длинный и нагруженный участок системы. За результатами этих вычислений и подбирается вентилятор.
Рассчитывая магистральную ветвь желательно, чтобы скорость в воздуховоде увеличивалась по ходу приближения к вентилятору!
Только не забывайте об увязке остальных ветвей системы. Это важно! Если нет возможности произвести увязку на ответвлениях воздуховодов в пределах 10% нужно применять диафрагмы. Коэффициент сопротивления диафрагмы рассчитывается за формулой:
Если неувязка будет больше 10%, когда горизонтальный воздуховод входит в вертикальный кирпичный канал в месте стыковки необходимо разместить прямоугольные диафрагмы.
Основная задача расчета состоит из нахождения потерь давления. Подбирая при этом оптимальный размер воздуховодов и контролирую скорость воздуха. Общие потери давления представляют собой сумму двух компонентов — потерь давления по длине воздуховодов (на трение) и потерь в местных сопротивлениях. Расчитываются они по формулам
Эти формулы правильны для стальных воздуховодов, для всех остальных вводится коэффициент поправки. Он берется из таблицы в зависимости от скорости и шероховатости воздуховодов.
Для прямоугольных воздухопроводов расчетной величиной принимается эквивалентный диаметр.
Рассмотрим последовательность аэродинамического расчета воздуховодов на примере офисов , приведенных в предыдущей статье, по формулам. А затем покажем как он выглядит в программке Excel.
Пример расчета
По расчетам в кабинете воздухообмен составляет 800 м3/час. Задание было запроектировать воздуховоды в кабинетах не больше 200 мм высотой. Размеры помещения даны заказчиком. Воздух подается при температуре 20°С, плотность воздуха 1,2 кг/м3.
Воздух подается при температуре 20°С, плотность воздуха 1,2 кг/м3.
Проще будет если результаты заносить в таблицу такого вида
Сначала мы сделаем аэродинамический расчет главной магистрали системы. Теперь все по-порядку:
- Разбиваем магистраль на участки по приточным решеткам. У нас в помещении восемь решеток, на каждую приходится по 100 м3/час. Получилось 11 участков. Вводим расход воздуха на каждом участке в таблицу.
- Записываем длину каждого участка.
- Рекомендуемая максимальная скорость внутри воздуховода для офисных помещений до 5 м/с. Поэтому подбираем такой размер воздуховода, чтобы скорость увеличивалась по мере приближения к вентиляционному оборудованию и не превышала максимальную. Это делается для избежания шума в вентиляции . Возьмем для первого участка берем воздуховод 150х150, а для последнего 800х250.
V1=L/3600F =100/(3600*0,023)=1,23 м/с.
V11= 3400/3600*0,2= 4,72 м/с
Нас результат устраивает. Определяем размеры воздуховодов и скорость по этой формуле на каждом участке и вносим в таблицу.
Определяем размеры воздуховодов и скорость по этой формуле на каждом участке и вносим в таблицу.
Исходные данные для вычислений
Когда известна схема вентиляционной системы, размеры всех воздухопроводов подобраны и определено дополнительное оборудование, схему изображают во фронтальной изометрической проекции, то есть аксонометрии. Если ее выполнить в соответствии с действующими стандартами, то на чертежах (или эскизах) будет видна вся информация, необходимая для расчета.
- С помощью поэтажных планировок можно определить длины горизонтальных участков воздухопроводов. Если же на аксонометрической схеме проставлены отметки высот, на которых проходят каналы, то протяженность горизонтальных участков тоже станет известна. В противном случае потребуются разрезы здания с проложенными трассами воздухопроводов. И в крайнем случае, когда информации недостаточно, эти длины придется определять с помощью замеров по месту прокладки.
- На схеме должно быть изображено с помощью условных обозначений все дополнительное оборудование, установленное в каналах.
 Это могут быть диафрагмы, заслонки с электроприводом, противопожарные клапаны, а также устройства для раздачи или вытяжки воздуха (решетки, панели, зонты, диффузоры). Каждая единица этого оборудования создает сопротивление на пути воздушного потока, которое необходимо учитывать при расчете.
Это могут быть диафрагмы, заслонки с электроприводом, противопожарные клапаны, а также устройства для раздачи или вытяжки воздуха (решетки, панели, зонты, диффузоры). Каждая единица этого оборудования создает сопротивление на пути воздушного потока, которое необходимо учитывать при расчете. - В соответствии с нормативами на схеме возле условных изображений воздуховодов должны быть проставлены расходы воздуха и размеры каналов. Это определяющие параметры для вычислений.
- Все фасонные и разветвляющие элементы тоже должны быть отражены на схеме.
Если такой схемы на бумаге или в электронном виде не существует, то придется ее начертить хотя бы в черновом варианте, при вычислениях без нее не обойтись.
Вернуться к оглавлению
С чего начинать?
Диаграмма потери напора на каждый метр воздуховода.
Очень часто приходится сталкиваться с достаточно простыми схемами вентиляции, в которых присутствует воздухопровод одного диаметра и нет никакого дополнительного оборудования. Такие схемы просчитываются достаточно просто, но что делать, если схема сложная с множеством ответвлений? Согласно методике просчета потерь давления в воздуховодах, которая изложена во многих справочных изданиях, нужно определить самую длинную ветвь системы либо ветку с наибольшим сопротивлением. Выяснить таковую по сопротивлению на глаз удается редко, поэтому принято вести расчет по самой протяженной ветви. После этого пользуясь величинами расходов воздуха, проставленных на схеме, всю ветку делят на участки по этому признаку. Как правило, расходы меняются после разветвлений (тройников) и при делении лучше всего ориентироваться на них. Бывают и другие варианты, например, приточные или вытяжные решетки, встроенные прямо в магистральный воздуховод. Если на схеме это не показано, а такая решетка имеется, потребуется расход после нее высчитать. Участки нумеруют начиная от самого удаленного от вентилятора.
Такие схемы просчитываются достаточно просто, но что делать, если схема сложная с множеством ответвлений? Согласно методике просчета потерь давления в воздуховодах, которая изложена во многих справочных изданиях, нужно определить самую длинную ветвь системы либо ветку с наибольшим сопротивлением. Выяснить таковую по сопротивлению на глаз удается редко, поэтому принято вести расчет по самой протяженной ветви. После этого пользуясь величинами расходов воздуха, проставленных на схеме, всю ветку делят на участки по этому признаку. Как правило, расходы меняются после разветвлений (тройников) и при делении лучше всего ориентироваться на них. Бывают и другие варианты, например, приточные или вытяжные решетки, встроенные прямо в магистральный воздуховод. Если на схеме это не показано, а такая решетка имеется, потребуется расход после нее высчитать. Участки нумеруют начиная от самого удаленного от вентилятора.
Вернуться к оглавлению
Методика. Площадь воздуховодов MagiCAD. Andrey Shirshov, PDF Free Download
Все прототипы В года
1. Прототип задания B9 ( 245359) Все прототипы В5 2013 года Найдите квадрат расстояния между вершинами и прямоугольного параллелепипеда, для которого,,. 2. Прототип задания B9 ( 245360) Найдите расстояние
Прототип задания B9 ( 245359) Все прототипы В5 2013 года Найдите квадрат расстояния между вершинами и прямоугольного параллелепипеда, для которого,,. 2. Прототип задания B9 ( 245360) Найдите расстояние
ИВЕНТ ПРАЙС-ЛИСТ 2018
ИВЕНТ ПРАЙС-ЛИСТ 2018 ОГЛАВЛЕНИЕ ВОЗДУХОВОД КРУГЛОГО СЕЧЕНИЯ СПИРАЛЬНОНАВИВНОЙ ИЗ ОЦИНКОВАННОЙ СТАЛИ… 2 ВОЗДУХОВОД КРУГЛОГО СЕЧЕНИЯ ПРЯМОШОВНЫЙ ИЗ ОЦИНКОВАННОЙ СТАЛИ… 3 ОТВОДЫ КРУГЛОГО СЕЧЕНИЯ ИЗ ОЦИНКОВАННОЙ
ПодробнееВоздуховоды Общие сведения
Воздуховоды Общие сведения Воздуховоды (прямые и фасонные части) прямоугольного и круглого сечения изготавливаются по видам и размерному ряду принятому в : — ВСН 353 86 «Проектирование и применение воздуховодов
ПодробнееВсе прототипы задания В9 (2013)
Все прототипы задания В9 (2013) ( 245359) Найдите квадрат расстояния между вершинами и прямоугольного параллелепипеда, для которого,,. ( 245360) Найдите расстояние между вершинами и прямоугольного параллелепипеда,
( 245360) Найдите расстояние между вершинами и прямоугольного параллелепипеда,
Воздуховоды круглого сечения
Воздуховоды Воздуховоды (прямые и фасонные части) прямоугольного и круглого сечения изготавливаются по видам и размерному ряду принятому в : — ВСН 353-86 «Проектирование и применение воздуховодов из унифицированных
Подробнее7. Задачи по стереометрии
РОСТОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ 7 Задачи по стереометрии методические указания для абитуриентов физического факультета Ростов-на-Дону 00 Печатается по решению учебнофакультета РГУ методической комиссии
ПодробнееВоздуховод круглый -2- Без фланцев. На фланцах. «Бабочка» Площадь живого сечения, Площадь поверхности 1 п.м., Вес 1 п.м. Толщина стали s, Цена,
Воздуховод круглый Диаметр Толщина стали s, Площадь поверхности 1 п.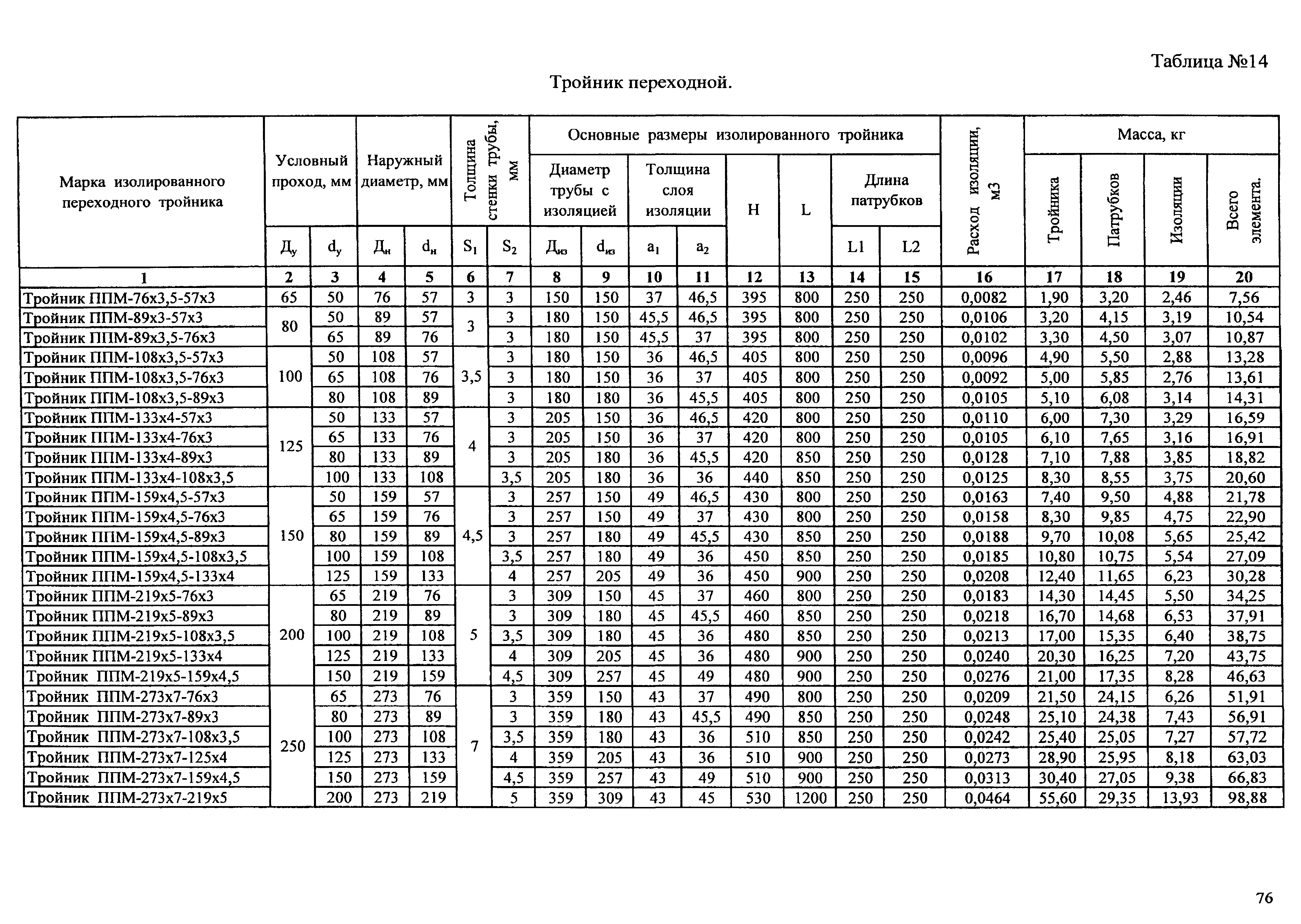 м., Площадь живого сечения, Вес 1 п.м. d, мм мм м 2 м 2 кг / м.п. 100 0,5 0,32 0,008 1,2 156 125 0,5 0,4 0,012 1,4 195 160 0,5 0,51 0,02
м., Площадь живого сечения, Вес 1 п.м. d, мм мм м 2 м 2 кг / м.п. 100 0,5 0,32 0,008 1,2 156 125 0,5 0,4 0,012 1,4 195 160 0,5 0,51 0,02
Runicom tel.:+7(495) Page 1 of 20
ВОЗДУХОВОДЫ ПРЯМОУГОЛЬНОГО СЕЧЕНИЯ ИЗ ОЦИНКОВАННОЙ СТАЛИ Толщина металла, Прямой участок длиной L = 1250 Длина прямого участка, Прямой участок длиной свыше 1250 в руб/м 2 Прямой участок длиной менее 1250
Подробнее3 ОСНОВНЫЕ ФОРМУЛЫ ДЛЯ СПРАВОК
Глава ОСНОВНЫЕ ФОРМУЛЫ ДЛЯ СПРАВОК.. Геометрия Треугольники. Два треугольника равны, если =, b = b, γ = γ ; c = c, α = α, β = β ; =, b = b, c = c.. Два треугольника подобны, если α = α, β = β ; b =, b
ПодробнееТригонометрические уравнения
Тригонометрические уравнения С б) Укажите корни, принадлежащие отрезку. а) Решите уравнение б) Укажите корни уравнения, принадлежащие отрезку а) Решbте уравнение. б) Укажите корни этого уравнения, принадлежащие
б) Укажите корни этого уравнения, принадлежащие
Прямоугольный параллелепипед
ЗАДАНИЕ 10 Стереометрия Куб 1.Площадь поверхности куба равна 18. Найдите его диагональ. 2. Диагональ грани куба равна 2 6. Найдите диагональ куба. 3. Диагональ грани куба равна 6. Найдите диагональ куба.
ПодробнееПРЯМОЙ И НАКЛОННЫЙ КОНУС
ПРЯМОЙ ЦИЛИНДР Пусть в пространстве заданы две параллельные плоскости и. F круг в одной из этих плоскостей, например. Рассмотрим ортогональное проектирование на плоскость. Проекцией круга F будет круг
ПодробнееМногогранники. Призма
Справка В9 Многогранники Многогранник это такое тело, поверхность которого состоит из конечного числа плоских многоугольников. Призма Призмой называется многогранник, который состоит из двух плоских многоугольников,
ПодробнееЗадачи по с т е р е о м е т р и и
Задачи по с т е р е о м е т р и и Ермак Елена Анатольевна, доктор педагогических наук, профессор кафедры математического анализа и методики обучения математике Псковского государственного университета
ПодробнееСХЕМА ИССЛЕДОВАНИЯ ФУНКЦИИ
СХЕМА ИССЛЕДОВАНИЯ ФУНКЦИИ 1. Найти область определения функции.. Исследовать четность и периодичность функции. 3. Исследовать точки разрыва, найти вертикальные асимптоты. 4. Найти наклонные асимптоты
Найти область определения функции.. Исследовать четность и периодичность функции. 3. Исследовать точки разрыва, найти вертикальные асимптоты. 4. Найти наклонные асимптоты
Прайс-лист на ВЕНТИЛЯЦИЮ
Прайс-лист на ВЕНТИЛЯЦИЮ Содержание 1. Прямые участки 2. 3. Сэндвич нержавеющая сталь 4. Отвод 5. Переход 6. Тройник 7. Врезка, Заглушка, Нипель 8. Гибкая вставка, Дефлектор, Обратный клапан 9. Дросель-клапан,
ПодробнееВсе прототипы заданий В года
1. Прототип задания B13 ( 27054) выходящие из одной вершины, равны 3 и 4. Площадь поверхности этого параллелепипеда равна 94. Найдите третье ребро, выходящее из той же вершины. Все прототипы заданий В13
ПодробнееЗадание 8, 14. Стереометрия
Задание 8, 4. Стереометрия Основные определения Аксиомы стереометрии Теорема. Через любые три точки, не лежащих на одной прямой, проходит плоскость, и притом только одна. Теорема. Если две точки прямой
Через любые три точки, не лежащих на одной прямой, проходит плоскость, и притом только одна. Теорема. Если две точки прямой
Все прототипы заданий года
1. Прототип задания 12 ( 27064) Правильная четырехугольная призма описана около цилиндра, радиус основания и высота которого равны 1. Найдите площадь боковой поверхности призмы. Все прототипы заданий 12
ПодробнееСОДЕРЖАНИЕ:
1 СОДЕРЖАНИЕ: ВОЗДУХОВОДЫ…….. 2 — Воздуховоды и фасонные детали круглого сечения…….. 3 — Зонты круглые……. 11 — Дефлектора круглые…. 12 — Насадки с водоотводящим кольцом…….. 13 — Вставки
ПодробнееКалендарно — тематический план
Календарно — тематический план ГЕОМЕТРИЯ Класс 11 Годовое количество часов 68 Количество часов в неделю — 2 Учебный год — 2013 2014 Учитель Беликова Галина Ивановна МКОУ «Борятинская СОШ» Согласовано зам.
Воздуховоды прямоугольного сечения
Воздуховоды прямоугольного сечения Из оцинкованной стали Цена в руб/м 2 Толщина металла, мм Прямой участок 0,55 без фланцев 306 0,55 на фланцах (шина No20) 379 0,7 без фланцев 336 0,7 на фланцах (шина
ПодробнееПрайс-лист на ВЕНТИЛЯЦИЮ
Прайс-лист на ВЕНТИЛЯЦИЮ Содержание 1. Прямые участки 2. 3. Сэндвич нержавеющая сталь 4. Отвод 5. Переход 6. Тройник 7. Врезка, Заглушка, Нипель 8. Гибкая вставка, Дефлектор, Обратный клапан 9. Дросель-клапан,
ПодробнееТест 250. Отрезок. Длина
Тест 250. Отрезок. Длина Длина отрезка равна 1, если он является: 1. высотой равностороннего треугольника со стороной 2; 2. третьей стороной треугольника, в котором две другие стороны равны 1 и 2, а угол
ПодробнееВоздуховоды и фасонные изделия
28. 12.2018 Воздуховоды и фасонные изделия ООО «СПН-Полимер» Воздуховоды круглого и прямоугольного сечения из полипропилена (ПП-С, ПП-Г) полиэтилена (ПНД) поливинилхлорида (ПВХ) Компания ООО «СПН — Полимер»
12.2018 Воздуховоды и фасонные изделия ООО «СПН-Полимер» Воздуховоды круглого и прямоугольного сечения из полипропилена (ПП-С, ПП-Г) полиэтилена (ПНД) поливинилхлорида (ПВХ) Компания ООО «СПН — Полимер»
Все прототипы заданий В года
1. Прототип задания B13 ( 27064) Правильная четырехугольная призма описана около цилиндра, радиус основания и высота которого равны 1. Найдите площадь боковой поверхности призмы. Все прототипы заданий
ПодробнееВоздуховоды и фасонные изделия
Воздуховоды и фасонные изделия Оцинкованные прямоугольные воздуховоды на фланце из шинорейки Прямоугольные воздуховоды из углеродистой стали Толщина стали,мм /Шина Размер изделия / Цена A,B 150, L>1250
ПодробнееВсе прототипы задания В11 (2013)
Все прототипы задания В11 (2013) ( 25541) Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые). ( 25561) Найдите площадь поверхности многогранника, изображенного
( 25561) Найдите площадь поверхности многогранника, изображенного
Технический комментарий
СОДЕРЖАНИЕ Технический комментарий Ниппельное соединение воздуховодов Заказ воздуховодов Прямой участок Отвод 900 Отвод 600 Отвод 450 Отвод 300 Отвод 150 Переходы Тройник Ниппель Муфта Врезка круглая Заглушка
ПодробнееПрограммы испытаний по математике
Программы испытаний по математике 1. Основные математические понятия и факты Арифметика, алгебра и начала анализа Натуральные числа (N). Простые и составные числа. Делитель, кратное. Наибольший общий делитель,
ПодробнееТест по теме «Задачи стереометрии»
Тест по теме «Задачи стереометрии» Тест составлен на основе учебника «Геометрия, 10-11 класс (базового и профильного уровней ) / Л.С. Атанасян и др. — М.: «Просвещение», 2010. Аннотация: Задачи теста соответствуют
— М.: «Просвещение», 2010. Аннотация: Задачи теста соответствуют
Основные определения, теоремы и формулы планиметрии.
Основные определения, теоремы и формулы планиметрии. Обозначения: AВС треугольник с вершинами А, B, С. а = BC, b = AС, с = АB его стороны, соответственно, медиана, биссектриса, высота, проведенные к стороне
ПодробнееСтереометрия: комбинации тел.
А.С. Крутицких и Н.С. Крутицких. Подготовка к ЕГЭ по математике. http://matematikalegko.ru Открытый банк заданий ЕГЭ по математике http://mathege.ru Стереометрия: комбинации тел. 27041. Прямоугольный параллелепипед
ПодробнееОнлайн калькулятор
Онлайн-калькулятор расчета производительности вентиляции
Расчет вентиляции, как правило, начинается с подбора оборудования, подходящего по таким параметрам, как производительность по прокачиваемому объему воздуха и измеряемому в кубометрах в час. Важным показателем в системе является кратность воздухообмена. Кратность воздухообмена показывает, сколько раз происходит полная замена воздуха в помещении в течение часа. Кратность воздухообмена определяется СНиП и зависит от:
Важным показателем в системе является кратность воздухообмена. Кратность воздухообмена показывает, сколько раз происходит полная замена воздуха в помещении в течение часа. Кратность воздухообмена определяется СНиП и зависит от:
- назначения помещения
- количества оборудования
- выделяющего тепло,
- количества людей в помещении.
В сумме все значения по кратности воздухообмена для всех помещений составляют производительность по воздуху.
Расчет производительности по кратности воздухообмена
Онлайн-калькулятор расчета системы вентиляцииСледующий этап в расчете вентиляции — проектирование воздухораспределительной сети, состоящей из следующих компонентов: воздуховоды, распределители воздуха, фасонные изделия (переходники, повороты, разветвители.) Сначала разрабатывается схема воздуховодов вентиляции, по которой производится расчет уровня шума, напора по сети и скорости потока воздуха. Напор по сети напрямую зависит от того, какова мощность используемого вентилятора и рассчитывается с учетом диаметров воздуховодов, количества переходов с одного диаметра на другой, и количества поворотов. Напор по сети должен возрастать с увеличением длины воздуховодов и количества поворотов и переходов. Расчет количества диффузоров
| ||||||||||||||||
Проектируя системы вентиляции, необходимо находить оптимальное соотношение между мощностью вентилятора, уровнем шума и диаметром воздуховодов. Расчет мощности калорифера производится с учетом необходимой температуры в помещении и нижним уровнем температуры воздуха снаружи.
Расчет мощности калорифера
| Методика расчета мощности калорифера Р = T * L * Сv / 1000, где: Р — мощность прибора, кВт; |
Также при выборе оборудования для системы вентиляции необходимо рассчитать следующие параметры:
- Производительность по воздуху;
- Мощность калорифера;
- Рабочее давление, создаваемое вентилятором;
- Скорость потока воздуха и площадь сечения воздуховодов;
- Допустимый уровень шума.
Такие потери пропорциональны динамическому давлению pд = ?v2/2, где ? — плотность воздуха, равная примерно 1,2 кг/м3 при температуре около +20 °C, а v — его скорость [м/с], как правило, за сопротивлением. Коэффициенты пропорциональности ?, называемые коэффициентами местного сопротивления (КМС), для различных элементов систем В и КВ обычно определяются по таблицам, имеющимся, в частности, в [2] и в ряде других источников.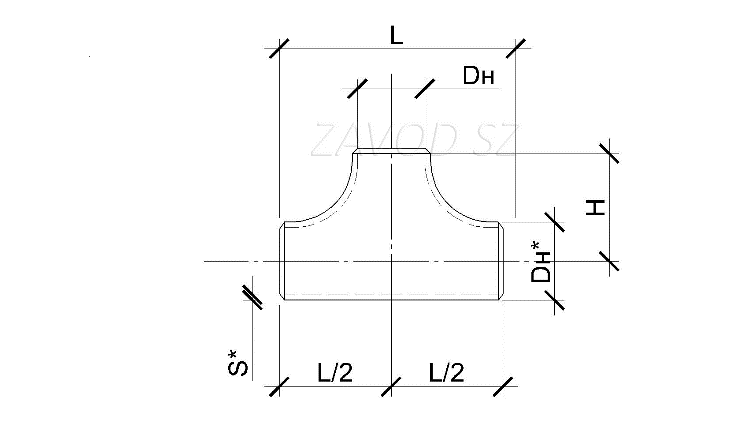 Наибольшую сложность при этом чаще всего вызывает поиск КМС для тройников или узлов ответвлений, поскольку в этом случае необходимо принимать во внимание вид тройника (на проход или на ответвление) и режим движения воздуха (нагнетание или всасывание), а также отношение расхода воздуха в ответвлении к расходу в стволе Lo? = Lo/Lc и площади сечения прохода к площади сечения ствола fn? = fn/fc. Для тройников при всасывании нужно учитывать еще и отношение площади сечения ответвления к площади сечения ствола fo? = fo/fc. В руководстве [2] соответствующие данные приведены в табл. 22.36–22.40. Наибольшую сложность при этом чаще всего вызывает поиск КМС для тройников или узлов ответвлений, поскольку в этом случае необходимо принимать во внимание вид тройника (на проход или на ответвление) и режим движения воздуха (нагнетание или всасывание), а также отношение расхода воздуха в ответвлении к расходу в стволе Lo? = Lo/Lc и площади сечения прохода к площади сечения ствола fn? = fn/fc. Для тройников при всасывании нужно учитывать еще и отношение площади сечения ответвления к площади сечения ствола fo? = fo/fc. В руководстве [2] соответствующие данные приведены в табл. 22.36–22.40.Однако, при больших относительных расходах в ответвлении КМС меняются весьма резко, поэтому в этой области рассматриваемые таблицы вручную интерполируются с трудом и со значительной погрешностью. Кроме того, в случае использования электронных таблиц MS Excel опять-таки желательно иметь формулы для непосредственного вычисления КМС через отношения расходов и сечений. При этом такие формулы должны быть, с одной стороны, достаточно простыми и удобными для массового проектирования и использования в учебном процессе, но, в то же время, не должны давать погрешность, превышающую обычную точность инженерного расчета. Представление о степени соответствия найденных соотношений и исходных значений КМС дает рис. 1, где показаны результаты обработки таблицы 22.37 для КМС унифицированных тройников (узлов ответвлений) на проход круглого и прямоугольного сечения при нагнетании. Примерно такая же картина получается и для аппроксимации табл. В то же время формулы, приведенные в настоящей работе, весьма просты, наглядны и легко доступны для инженерных расчетов, особенно в MS Excel, а также в учебном процессе. 1. А.Д. Альтшуль, Л.С. Животовский, Л.П. Иванов. Гидравлика и аэродинамика. — М.: Стройиздат, 1987. |
Калькулятор воздуховодов – жестянка.com
1. Расчёт ПРЯМЫХ УЧАСТКОВ прямоугольных воздуховодов
Высота, А (мм)
Ширина, В (мм)
Длина участка, L (м)
Толщина металла, t (мм)0,40,50,550,60,70,80,91,01,2
Тип металлаОц. стальНерж.сталь
стальНерж.сталь
Тип соединительных элементов на торцеШинаРейкаНет
Вес элемента, кг
Площадь поверхности, м.кв
Количество элементов
Стоимость элемента, руб
Запись в спецификацию
2. Расчёт ПРЯМЫХ УЧАСТКОВ круглых воздуховодов
Диаметр воздуховода, D (мм)
Длина участка, L (м)
Толщина металла, t (мм)0,40,50,550,60,70,80,91,01,2
Тип металлаОц. стальНерж.сталь
Тип соединительных элементов на торцеФланецНиппельНет
Вес элемента, кг
Площадь поверхности, м.кв
Количество элементов
Стоимость элемента, руб
Запись в спецификацию
3. Расчёт ОТВОДА для прямоугольных воздуховодов
Высота, А (мм)
Ширина, B (мм)
Угол поворота, α (°)904530
Толщина металла, t (мм)0,40,50,550,60,70,80,91,01,2
Тип металлаОц. стальНерж.сталь
Тип соединительных элементов на торцеШинаРейкаНет
Вес элемента, кг
Площадь поверхности, м. кв
кв
Количество элементов
Стоимость элемента, руб
Запись в спецификацию
4. Расчёт ОТВОДА для круглого воздуховода
Диаметр воздуховода, D (мм)
Угол поворота, α (°)904530
Толщина металла, t (мм)0,40,50,550,60,70,80,91,01,2
Тип металлаОц. стальНерж.сталь
Тип соединительных элементов на торцеФланецНиппельНет
Вес элемента, кг
Площадь поверхности, м.кв
Количество элементов
Стоимость элемента, руб
Запись в спецификацию
5. Расчёт ПЕРЕХОДА СЕЧЕНИЯ для прямоугольного воздуховода
Высота начальная, А (мм)
Ширина начальная, B (мм)
Высота конечная, a (мм)
Ширина конечная, b (мм)
Толщина металла, t (мм)0,40,50,550,60,70,80,91,01,2
Тип металлаОц. стальНерж.сталь
Тип соединительных элементов на торцеШинаРейкаНет
Вес элемента, кг
Площадь поверхности, м.кв
Количество элементов
Стоимость элемента, руб
Запись в спецификацию
6.
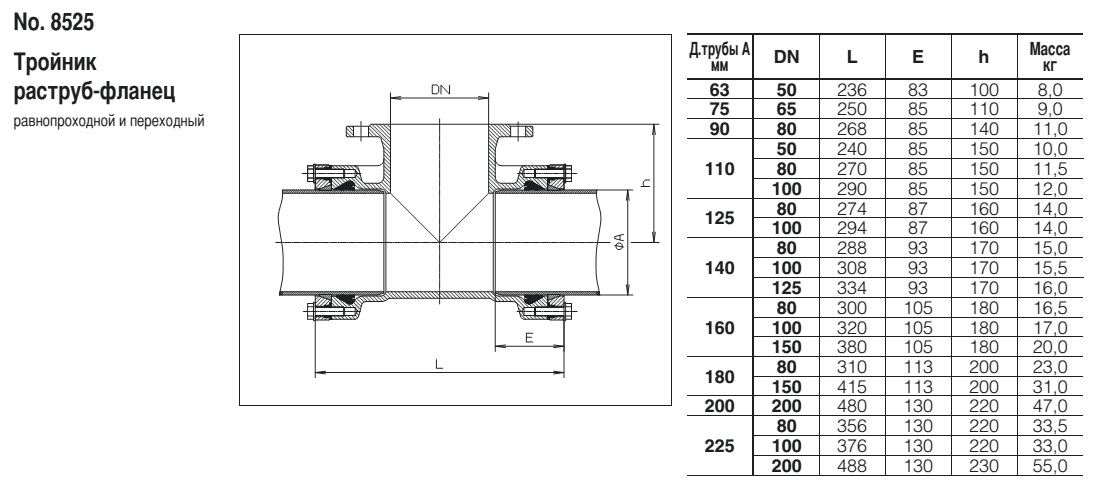 Расчёт ПЕРЕХОДА СЕЧЕНИЯ для круглого воздуховода
Расчёт ПЕРЕХОДА СЕЧЕНИЯ для круглого воздуховодаДиаметр начальный, D (мм)
Диаметр конечный, d (мм)
Толщина металла, t (мм)0,40,50,550,60,70,80,91,01,2
Тип металлаОц. стальНерж.сталь
Тип соединительных элементов на торцеФланецНиппельНет
Вес элемента, кг
Площадь поверхности, м.кв
Количество элементов
Стоимость элемента, руб
Запись в спецификацию
7. Расчёт ПЕРЕХОДА с круглого на прямоугольное сечение
Высота начальная, А (мм)
Ширина начальная, B (мм)
Диаметр конечный, D (мм)
Толщина металла, t (мм)0,40,50,550,60,70,80,91,01,2
Тип металлаОц. стальНерж.сталь
Тип соединительных элементов на торцеШина-ФланецРейка-НиппельНет
Вес элемента, кг
Площадь поверхности, м.кв
Количество элементов
Стоимость элемента, руб
Запись в спецификацию
8. Расчёт ТРОЙНИКА для прямоугольного воздуховода
Высота главного воздуховода, А (мм)
Ширина главного воздуховода, B (мм)
Высота врезки, a (мм)
Ширина врезки, b (мм)
Угол врезки, α (°)9045
Толщина металла, t (мм)0,40,50,550,60,70,80,91,01,2
Тип металлаОц. стальНерж.сталь
стальНерж.сталь
Тип соединительных элементов на торцеШинаРейкаНет
Вес элемента, кг
Площадь поверхности, м.кв
Количество элементов
Стоимость элемента, руб
Запись в спецификацию
9. Расчёт ТРОЙНИКА для круглого воздуховода
Диаметр главного воздуховода, D (мм)
Диаметр врезки, d (мм)
Толщина металла, t (мм)0,40,50,550,60,70,80,91,01,2
Тип металлаОц. стальНерж.сталь
Тип соединительных элементов на торцеФланецНиппельНет
Вес элемента, кг
Площадь поверхности, м.кв
Количество элементов
Стоимость элемента, руб
Запись в спецификацию
Расчет герметичности приварных тройников
Существует как минимум три признанных метода оценки пересечений ветвей. Чаще всего они применяются к сборным соединениям сосудов под давлением и трубопроводам, а не к сварным тройникам.
Сварные тройники по ASME B16.9 обычно проходят испытания на разрыв поставщиком, но это не помогает, если вам нужно оценить корродированный или эродированный фитинг или вы хотите проверить приобретенный фитинг. (В одной статье от 2014 года, PVP2014-28265 , были обнаружены несоответствующие фитинги, выходящие из строя ниже требуемого давления разрыва).Другой стандарт, EN10253, дает рекомендуемые толщины фитингов и методы расчета.
(В одной статье от 2014 года, PVP2014-28265 , были обнаружены несоответствующие фитинги, выходящие из строя ниже требуемого давления разрыва).Другой стандарт, EN10253, дает рекомендуемые толщины фитингов и методы расчета.
Для расчета давления сварных тройников мы рассмотрим и сравним три метода Кодекса и другой подход из недавнего исследования. Рассматриваются следующие методы:
| № | Метод | Каталожный номер |
|---|---|---|
| 1 | Замена участка | ASME B31.3, ASME VIII Div. 1, PVP2014-28265 |
| 2 | Зона давления | EN13445, EN13480, ASME VIII Div 2, EN10253 |
| 3 | Местное напряжение | PD 5500 |
| 4 | Местное напряжение | PVT-17-1119 |
Метод замещения площадей, пожалуй, наиболее знаком инженерам-механикам.Площадь подпорной стенки давления удалена должна быть заменена на достаточную толщину в локально окружающий металл. Обычно он не используется для сварки тройников, однако способ его применения будет разработан в этой статье.
Обычно он не используется для сварки тройников, однако способ его применения будет разработан в этой статье.
Метод площади давления берет свое начало в Келлогге «Проектирование трубопроводных систем». Идея состоит в том, что давление, умноженное на площадь удерживаемой жидкости, должно быть приравнено к допустимому напряжению, умноженному на площадь металла. Он был принят в европейских нормах, таких как EN13445-3, EN13480-3, а совсем недавно в ASME VIII Division 2.Стандарт EN10253 для фитингов включает примеры того, как рассчитать адекватность удержания давления.
Метод PD5500 основан на исследовании локальных напряжений в ответвлениях сосудов высокого давления в 1960-х годах.
Четвертый метод — это, по сути, локальная проверка напряжения в области промежности тройника. Он основан на теории оболочек с эмпирической поправкой, чтобы привести ее в соответствие с результатами FEA.
Для большинства из этих подходов вам необходимо знать радиус и толщину промежности (как показано ниже). Это может не быть проблемой для фитингов, приобретенных в соответствии с EN10253, поскольку в этом стандарте указаны рекомендуемые значения толщины и радиуса. Для фитингов ASME B16.9 вам необходимо измерить фактический фитинг, чтобы получить информацию. Толщина стенки может быть измерена, например, с помощью ультразвукового датчика.
Это может не быть проблемой для фитингов, приобретенных в соответствии с EN10253, поскольку в этом стандарте указаны рекомендуемые значения толщины и радиуса. Для фитингов ASME B16.9 вам необходимо измерить фактический фитинг, чтобы получить информацию. Толщина стенки может быть измерена, например, с помощью ультразвукового датчика.
Метод замещения площади
В кодах B31 этот метод обычно применяется к сфабрикованным перекресткам. Он также применяется к экструдированным тройникам, однако этот подход довольно неудобен и предполагает встраивание прямоугольников в изогнутые секции
В кодах не указан метод оценки сварных тройников, однако изогнутый профиль сварного тройника хорошо поддается простому расчету.Эта проблема была рассмотрена в документе ASME от 2014 г., «Испытания на разрыв сварных тройников B16.9», PVP2014-28265, , в котором было дано уравнение для толщины.
[уравнение 1a]
В приведенном выше примере первый член представляет собой A2, второй — A4 (область промежности), а A3 консервативно установлено равным нулю.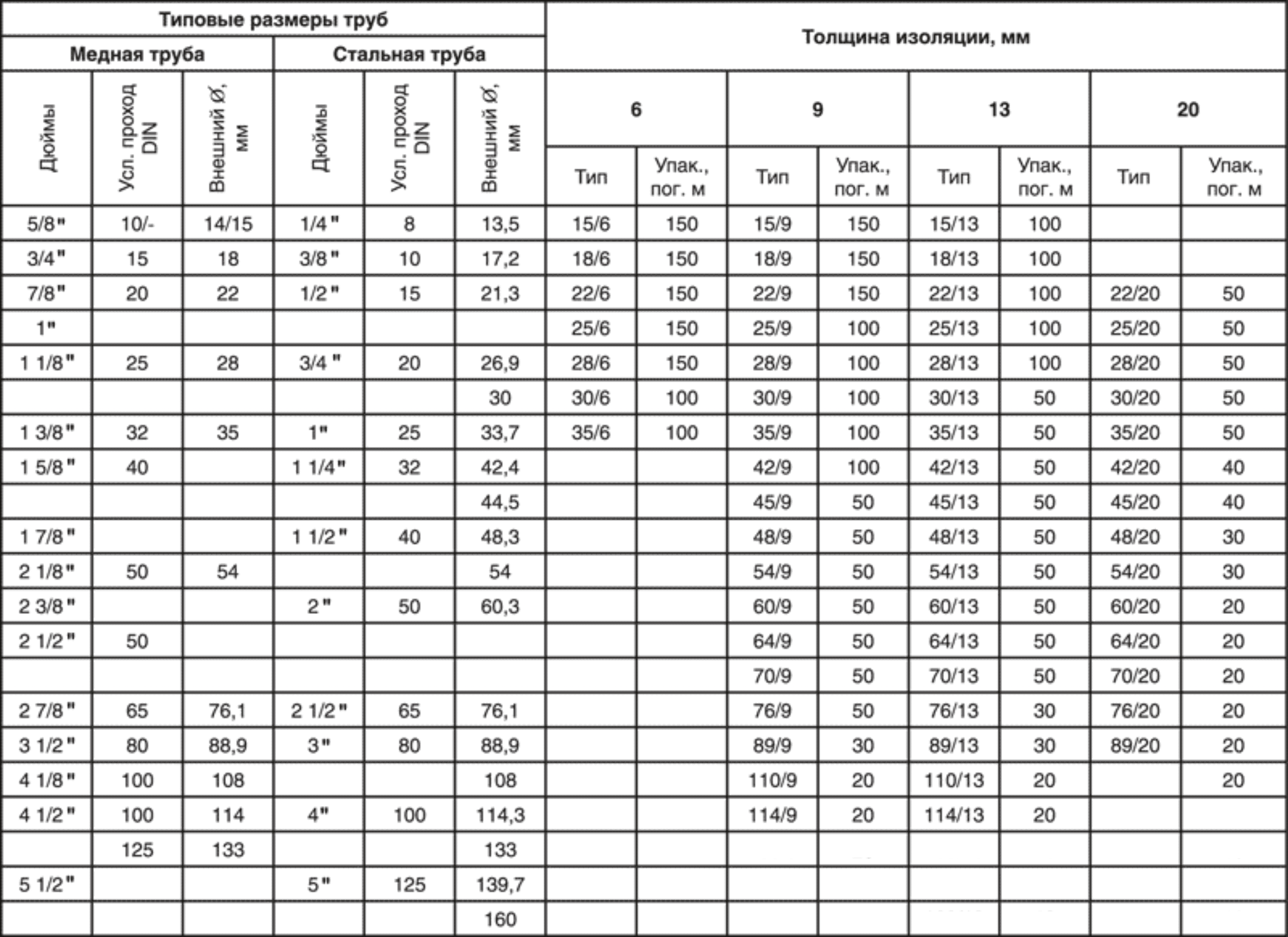 Коэффициент K взят из ASME B31.3 Cl. 304.3.4 (e), и изменяется от 1 для полноразмерных перекрестков до 0,7 для небольших ответвлений (Db / Dh <= 0,15). Этот фактор не фигурирует ни в формулах замены площади для сборных тройников, ни в ASME VIII Div.1 способ.
Коэффициент K взят из ASME B31.3 Cl. 304.3.4 (e), и изменяется от 1 для полноразмерных перекрестков до 0,7 для небольших ответвлений (Db / Dh <= 0,15). Этот фактор не фигурирует ни в формулах замены площади для сборных тройников, ни в ASME VIII Div.1 способ.
Уравнение 1a дает хорошее начало, но на самом деле это не было основной темой статьи. Так что давайте сделаем этот подход более строгим с помощью следующих изменений —
- используйте радиус кривизны осевой линии для расчета длины арматуры для A4
- разделить A4 на две области — «сторона заголовка» (первые 45 градусов промежности) и «сторона ответвления» (оставшаяся часть).
- Уменьшите длину A2 так, чтобы он останавливался в начале области промежности
- ограничивает зоны армирования до B31.3 предела для экструдированных тройников, но не дальше концов фитинга (минус однократная толщина для сужения)
- считать арматуру в филиале, если в пределах (регион А3)
Установка пределов армирования:
, где C и M указаны ниже:
Предельный угол для армирования:
Это приводит к следующей форме уравнения для проверки замены области.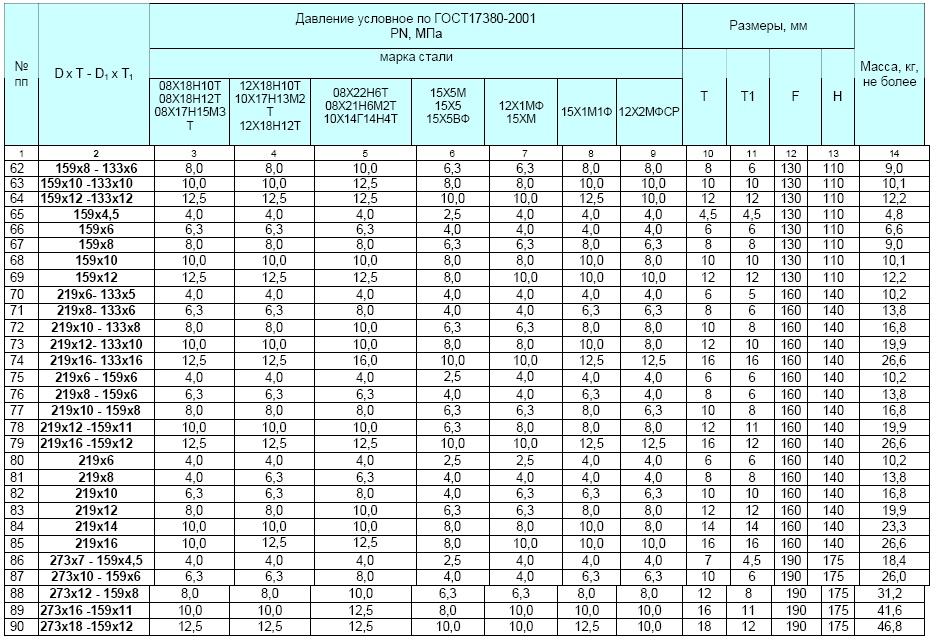
[ур. 1b]
Это основано на постоянстве по всей промежности — в качестве альтернативы можно заменить на в третьем члене и при вычислении альфа.
Для проектирования мы можем принять постоянную толщину на всем протяжении фитинга () и принять предположение для толщины ластовицы, кратной соответствующей номинальной толщине коллектора,. Используйте это для первой оценки и вычисления следующего уравнения:
[уравнение 1c]
Затем мы выполняем итерацию, пока значение N не сойдется.
Следует отметить, что ни одна из этих версий метода замены области не одобряется каким-либо Кодексом. На этом этапе я бы также с осторожностью использовал коэффициент К меньше единицы, пока не будет доказан его адекватность в этом приложении.
Общие проблемы с методом замены области *
- Нет согласия относительно расстояний, на которых должен быть размещен армирующий материал, чтобы быть эффективным
- Правило не основано ни на количественной оценке пиковых напряжений, ни на теоретических моделях.

- Не обеспечивает единообразный коэффициент безопасности для всего диапазона геометрий заголовка / ответвления.Нет постоянного запаса в отношении износа, деформации или усталости.
- В толстостенном оборудовании может образовываться чрезмерно жесткая конструкция (с сопутствующими проблемами при сварке готовых пересечений).
* Арт. PD 6550 Часть 2 Пояснительное дополнение к BS5500: 1988
Метод площади давления
Перекресток разбит на 4 квадранта для оценки. Оценка производится в соответствии с уравнением 2:
.Изучая формулу, мы можем видеть, что увеличение диаметра коллектора или ответвления увеличивает площадь давления в квадранте, что требует более толстой стенки.Если мы сделаем шаг назад и рассмотрим это, на самом деле это просто обобщение основной формулы кольцевого напряжения. Следующее — для цилиндра; аналогичный подход может быть использован для вывода уравнения для сферы.
На единицу длины:
или
Метод немного отличается от оригинального подхода Келлогга, в котором интенсивность напряжения учитывалась путем добавления половины давления к напряжению.
Формулы
Поскольку в фактических расчетах задействовано большое количество уравнений, они здесь не воспроизводятся.Вместо этого обратитесь к EN10253-2, раздел A.5.2.
Ограничения
- Толщина стенки и применяется по всему периметру трассы и ответвления соответственно. На переходах между прогоном и ответвлением (промежностной зоной) внутренняя и внешняя поверхности должны плавно сливаться.
- Минимальная толщина стенки на участке не должна превышать минимальную толщину стенки на участке.
Проблемы с методом «давление — площадь»
Проблемы с этим методом, похоже, аналогичны проблемам с методом замены области, а именно
- Не существует очевидного универсального закона, определяющего расстояния, на которых должен производиться расчет армирования
- Не основан на количественной оценке пиковых напряжений
- Не обеспечивает единообразный коэффициент безопасности для всего диапазона геометрий заголовка / ответвления.
 Нет постоянного запаса в отношении износа, деформации или усталости.
Нет постоянного запаса в отношении износа, деформации или усталости.
Уравнения метода EN здесь не приводятся. См. EN10253-2 Приложение A для полной демонстрации метода.
PD5500
Раздел 3.5.4.3 PD5500 содержит метод расчета соединений сопел резервуара путем ограничения местного напряжения, основанный на работе Leckie & Penny (1963). Предполагается, что пересечение находится под прямым углом, то есть влияние закругленного пересечения не распознается.
Чтобы применить этот метод к сварке тройников, сначала выберите значение и рассчитайте, как показано ниже:
Уравнение следует повторять до тех пор, пока оно не сходится. Затем проводится следующая проверка:
В этих формулах и — средний диаметр коллектора и ответвления соответственно.
Проблемы с методом PD5500
Этот метод прост и быстр в применении, однако он может не учитывать влияние размера подгонки — i.е. можно предположить, что зона усиления больше, чем имеется в фитинге трубы.
ПВТ-17-1119
В этой статье теория оболочки используется для расчета теоретического напряжения мембраны в промежности тройника. Расчетное напряжение переоценивает фактическое напряжение из-за усиливающего действия прямой трубы и быстро меняющейся кривизны в этой области. Однако, используя эмпирическое уравнение, оно затем корректируется так, чтобы оно достаточно хорошо соответствовало напряжениям, полученным при анализе методом конечных элементов.Утверждается, что уравнение обычно составляет от 0 до 15% с консервативной стороны для рассматриваемого диапазона геометрий.
Формулы
Хотя и не слишком сложный, из-за количества уравнений и необходимости применения численного дифференцирования этот метод здесь не воспроизводится.
Проблемы с методом PVT-17-1119
Этот подход имеет ограничения по параметрам геометрии и толщины из-за диапазона фитингов, рассмотренных в исследовании.
Одно интересное отличие этого метода состоит в том, что меньший радиус ластовицы приводит к более высокому локальному напряжению и увеличению требуемой толщины стенки. Оба метода замены площади давления и площади предполагают противоположное с точки зрения требуемой толщины стенки. Испытания на разрыв в целом согласны с тем, что меньший радиус ластовицы для идентичного в остальном сварного тройника имеет большую пропускную способность. Хотя вначале напряжения могут быть выше, дополнительный окружающий металл восполняет их по мере увеличения текучести.
Оба метода замены площади давления и площади предполагают противоположное с точки зрения требуемой толщины стенки. Испытания на разрыв в целом согласны с тем, что меньший радиус ластовицы для идентичного в остальном сварного тройника имеет большую пропускную способность. Хотя вначале напряжения могут быть выше, дополнительный окружающий металл восполняет их по мере увеличения текучести.
Это демонстрирует недостатки методов анализа упругости при использовании для герметизации сложных компонентов. Однако подход локального напряжения может быть уместным, когда вызывают беспокойство такие проблемы, как усталость или коррозионное растрескивание под напряжением.
Краткое сравнение методов
Требуемая толщина была рассчитана каждым методом для четырех вариаций геометрии (при условии постоянной толщины на каждом сварном тройнике). Значение K было установлено на 1 для вычислений замещения площади.
Примечательным результатом сравнения является замечательное согласие между подходами замещения площади давления и площади. Однако мы только что рассмотрели небольшой образец арматуры, поэтому не будем делать здесь однозначных выводов.
Однако мы только что рассмотрели небольшой образец арматуры, поэтому не будем делать здесь однозначных выводов.
Метод PD5500 неизменно позволяет получать самые тонкие или почти самые тонкие стенки. Это подтверждает возможность того, что некоторые тройники имеют меньшую длину арматуры, чем предполагается для этого уравнения (которое предназначено для сосудов).
PVT-17-1119 результаты варьировались от менее до более консервативных, хотя в основном они склонялись к консервативной стороне. Для этих расчетов местные напряжения были ограничены (допустимое напряжение ASME B31.3 для A106 Gr. B). Согласно ASME VIII Div. 2, теперь можно позволить локальным напряжениям достигать предела текучести для определенных материалов и рабочих условий, однако для этого сравнения это даст «несправедливое преимущество», поскольку давление, используемое для расчета, основано на кольцевом напряжении номинальной стенки.
Заключение
На данный момент метод площади давления, приведенный в EN10253-2, является единственным полностью кодифицированным подходом к сварке тройников. Показанный здесь метод замены площадей дает аналогичные результаты, и эта концепция знакома большинству инженеров, однако его использование со сварными тройниками не описано в кодах. Метод PD5500 позволяет получить самые тонкие стенки и может не учитывать влияние размеров фитинга. PVT-17-1119 имеет тенденцию требовать в среднем более толстой стенки, поскольку он пытается удерживать локальные мембранные напряжения в пределах нормы и имеет типичный предел погрешности в диапазоне от 0 до + 15%.
Показанный здесь метод замены площадей дает аналогичные результаты, и эта концепция знакома большинству инженеров, однако его использование со сварными тройниками не описано в кодах. Метод PD5500 позволяет получить самые тонкие стенки и может не учитывать влияние размеров фитинга. PVT-17-1119 имеет тенденцию требовать в среднем более толстой стенки, поскольку он пытается удерживать локальные мембранные напряжения в пределах нормы и имеет типичный предел погрешности в диапазоне от 0 до + 15%.
Martin помогает клиентам не упускать из виду проблемы с трубопроводом высокого давления и целостностью оборудования с помощью анализа напряжений, FEA и пригодности к эксплуатации. Его недавняя исследовательская работа по сварке тройников была опубликована в журнале ASME PVT. Он является автором различного программного обеспечения для трубопроводов, включая плагин X313 excel для допустимых напряжений B31.3, постпроцессор Salad для пользователей CAESAR II и веб-приложения на этом сайте.
СвязанныеТройник (Т) профиль свойства | calcresource
Определения
Оглавление
Геометрия
Площадь A и периметр P поперечного сечения тройника можно найти с помощью следующих формул:
\ begin {split} & A & = b t_f + (h-t_f) t_w \\ & P & = 2b + 2h \ end {split}
Расстояние от центра тяжести до верхнего края можно вычислить, если учесть, что первый момент площади (также называемый статическим моментом ) всего Т-образного сечения должно быть равным совокупным статическим моментам стенки и полки:
Ay_c = (t_w h) {h \ over2} + \ Big (\ left (b-t_w \ right) t_f \ Big) {t_f \ over2} \ Rightarrow
y_c = \ frac {1} {2A} \ left (t_w h ^ 2 + (b-t_w) {t_f} ^ 2 \ right)
У нас есть специальная статья о нахождение центра тяжести составной области. 3} {12}
3} {12}
Момент инерции (второй момент или площадь) используется в теории балок для описания жесткости балки при изгибе. Изгибающий момент M, приложенный к поперечному сечению, связан с его моментом инерции следующим уравнением:
M = E \ times I \ times \ kappa
где E — модуль Юнга, свойство материала, и \ kappa, кривизна балки из-за приложенной нагрузки. Следовательно, из предыдущего уравнения можно увидеть, что когда к поперечному сечению балки прилагается определенный изгибающий момент M, развиваемая кривизна обратно пропорциональна моменту инерции I.
Полярный момент инерции описывает жесткость поперечного сечения по отношению к крутящему моменту, аналогично планарные моменты инерции, описанные выше, связаны с изгибом при изгибе. Расчет полярного момента инерции I_z вокруг оси zz (перпендикулярно сечению) можно выполнить с помощью теоремы о перпендикулярных осях:
I_z = I_x + I_y
, где I_x и I_y — моменты инерции вокруг осей xx и yy, которые взаимно перпендикулярны zz и встречаются в общем начале.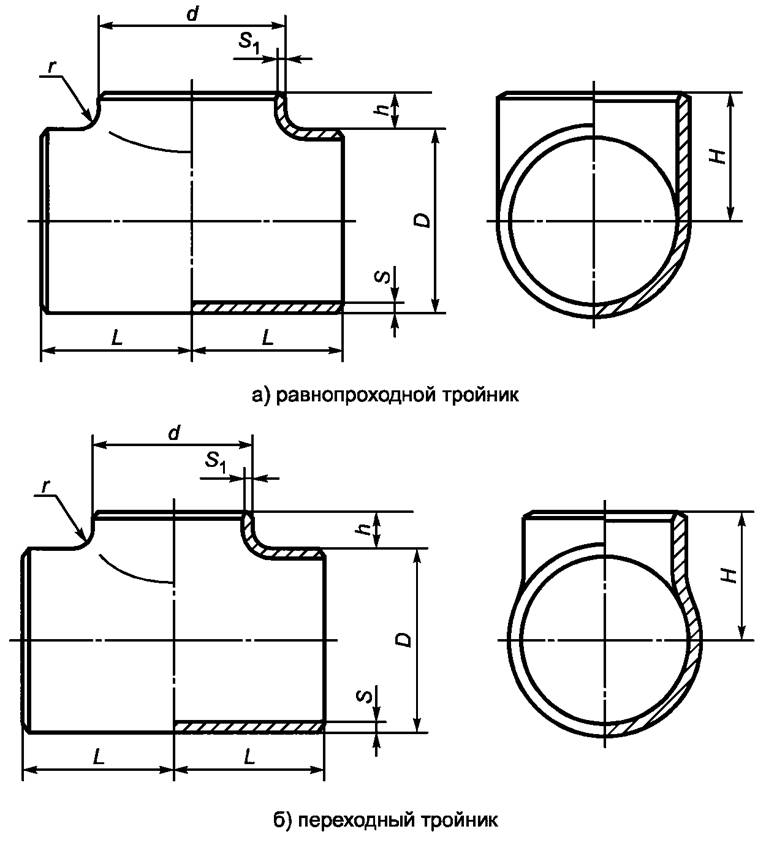 4.
4.
Модуль упругости
Модуль упругости S_x сечения любого поперечного сечения вокруг оси x-x, которая является центроидальной, описывает реакцию сечения при упругом изгибе при изгибе вокруг той же оси. Он определяется как:
S_x = \ frac {I_x} {Y}
, где I_x — момент инерции секции вокруг оси x, а Y — смещение от центра тяжести секции волокна параллельно оси x-x. Обычно представляет интерес самое удаленное волокно. Для Т-образного сечения модуль упругости S_x сечения вокруг оси x-x не является одинаковым для верхнего и нижнего конца волокна.Поскольку Т-образное сечение не является симметричным относительно оси x, расстояния двух концевых волокон (верхнего и нижнего) от этой оси различаются. Чем больше Y, тем меньше S_x, что обычно предпочтительнее для дизайна секции. Следовательно:
S_ {x, min} = \ frac {I_x} {h-y_c}
, где обозначение «min» основано на предположении, что y_c Для модуля сечения S_y вокруг оси yy, который для Т-образного сечения оказывается осью симметрии, модуль сечения находится по следующей формуле: S_y = \ frac {I_y} {X} \ Стрелка вправо S_y = \ frac {2 I_y} {b} Если изгибающий момент M_x приложен вокруг оси xx, сечение будет реагировать нормальными напряжениями, линейно изменяющимися с расстоянием от нейтральной оси (которое в упругом режиме совпадает с центроидальная ось xx). Модуль упругости пластического сечения аналогичен модулю упругого сечения, но определяется исходя из предположения о полной пластической текучести сечения из-за изгиба при изгибе. В этом случае вся секция делится на две части, одну на растяжение, а другую на сжатие, каждая из которых находится в однородном поле напряжений. Для материалов с равными напряжениями текучести при растяжении и сжатии это приводит к разделению сечения на две равные области, A_t при растяжении и A_c при сжатии, разделенных нейтральной осью.Эта ось называется пластиковой нейтральной осью , и для несимметричных участков не совпадает с упругой нейтральной осью (которая снова является центроидальной). Модуль упругости пластического сечения задается общей формулой: Z = A_c Y_c + A_t Y_t , где Y_c — расстояние от центра тяжести области сжатия A_c от нейтральной оси пластика, а Y_t — соответствующее расстояние от центра тяжести растяжения площадь А_т. В случае Т-образного сечения при изгибе xx положение пластиковой нейтральной оси может быть определено одним из следующих двух уравнений: \ left \ {\ begin {array} { ll} (h-y_ {pna}) t_w = \ frac {A} {2} & \ text {, if} y_ {pna} \ ge t_f \\ y_ {pna} b = \ frac {A} {2} & \ text {, if} y_ {pna} \ lt t_f \\ \ end {array} \ right. , что становится: y_ {pna} = \ left \ {\ begin {array} {ll} h- \ frac {A} {2t_w} & \ text {, если:} t_f \ le {A \ over2 b } \\ \ frac {A} {2b} & \ text {, если:} t_f \ gt {A \ over2 b} \\ \ end {array} \ right. где y_ \ textit {pna} расстояние пластиковой нейтральной оси от верхнего края фланца. Первое уравнение справедливо, когда пластиковая нейтральная ось проходит через стенку, а второе -, когда ось проходит через фланец. Как правило, заранее невозможно узнать, какое уравнение имеет значение.2} {4} \ end {split} Радиус вращения R g поперечного сечения относительно оси определяется по формуле: R_g = \ sqrt {\ frac {I} {A}} , где I момент инерции поперечного сечения относительно той же оси и A его площадь. Вам нравится эта страница? Сообщите об этом своим друзьям! Дата : 八 13, 2020 Категории : Новости компании / Просмотры новостей : 453 просмотра Тройник равный — один из наиболее часто используемых фитингов для труб, он широко используется во многих отраслях промышленности. Мы должны рассчитывать объем при транспортировке продукции.Методы расчета одинаковых тройников различаются для разных производственных процессов. Формула равного объема тройника Объем одинаковых тройников легче рассчитать, поскольку их прямые формы можно рассматривать как прямые трубы, соединенные друг с другом. Таким образом, вы можете рассчитать его объем как прямые трубы. Следовательно, вы должны знать внутренний радиус равного тройника и его высоту ( или длина) участка и ответвления. Объем = пи (или 3,14) x радиус в квадрате x высота. Таким образом можно получить примерный объем равного тройника ASME B16.9 Тройник под приварку встык Иногда вам нужно знать объем, когда у вас есть только диаметр и график или давление, что делать? Диаграмма объема может помочь вам решить проблему. Бесшовные тройник и сварной тройник (равный тройник ERW) являются тройниками под сварку встык, стандарт спецификации — ASME B16.9. Они имеют большой диапазон размеров, поэтому перечислить все значения невозможно. Приварной стык равного объема тройника изменяется только в зависимости от их номинального размера, вы можете быстро найти значение объема. Тройник под сварку внахлест По размерам он больше похож на тройник с резьбой, хотя представляет собой сварное соединение, аналогичное тройнику, сваренному встык. Размеры от 1/8 до 4 дюймов, классы давления — 3000, 6000 и 9000. Объем муфтовой сварки составляет связаны с этими двумя факторами. По размерам он больше похож на тройник с резьбой, хотя это фитинг под приварку, как тройник под сварку. Диапазон размеров — от 1/8 до 4 дюймов, номинальное давление — Класс 3000, Класс 6000 и Класс 9000. Размер и давление влияют на объем тройника, сваренного с раструбом. Тройник равный с резьбой Тройник с резьбой и тройник, приваренный муфтой, выкованы в соответствии с ASME B16.11 стандартных и имеют одинаковый размерный диапазон, поэтому их объемные диаграммы имеют одинаковое значение. Что еще более важно, все объемы на диаграмме — это объем контура и пространство, занимаемое упаковкой одного продукта, другими словами, это объем упакованного продукта. Имеется расчет объема приварного равномерного тройника и резьбового равного тройника: Крис Майл Я хотел как-то разобраться с этим вопросом, потому что это действительно большое дело, и я видел несколько полусырых ответов на этот вопрос. В моей книге каждый гольфист должен иметь возможность поразить пар-тройку за один бросок, пар-четверку за два и пар-пятерку за три. Если это невозможно, значит, вы играете слишком длинный курс, и если вы играете слишком длинный или слишком короткий курс, вы не получите должного удовольствия от игры. Расчет идеального расстояния до курса. Ответ на вопрос, сколько времени должен быть у вас курс, очень прост. Это 28. Просто умножьте для вас длину удачного драйва на 28, и это, по моему мнению, и есть длина трассы, на которой будет сложно, но приятно играть. Логика, лежащая в основе «Driver x 28», заключается в том, что идеальное поле будет иметь комбинацию легких, умеренно сложных и сложных лунок. Зная продолжительность поездки, вы можете оценить, как далеко вы попали в другие клубы.Например, большинство игроков в гольф бьют своим 6 айроном на 64% дистанции своего водителя. Если средняя дистанция пар 4 — это драйв, а пара № 6 — железо, вы знаете, что длина хорошего пар четыре для вас составляет 164% от расстояния вашего драйва. Имея эту информацию, а также определения для коротких, средних и длинных лунок, вы можете рассчитать общее расстояние для идеального курса на основе пройденного вами расстояния. Теперь единственное, что вам нужно знать, — это расстояние ваших точных ударов с мишени. Как создавался «Драйвер x 28». Нам нужно знать только две вещи, чтобы создать идеальную длину дистанции. (1) Нам нужно знать, как далеко вы попали по каждой клюшке в своей сумке, и (2) нам нужно определить, какие клюшки вы попали в каждую лунку на мифическом идеальном поле. И то, и другое намного проще, чем можно было ожидать! №1.Определите, как далеко вы попали во все свои клюшки. Зная, как далеко вы ударили водителя, мы можем предсказать, как далеко вы нанесете удар по всем клюшкам в своей сумке. Очевидно, это не будет точно для каждого игрока в гольф, но будет близко. Самая сложная часть этого — получить хорошую оценку общего расстояния вашего водителя для хорошо сбитого с толку водителя. В таблице ниже показано, как далеко типичный игрок попадает в каждую клюшку относительно расстояния, на которое он проехал. Эта информация взята из анализа TrackMan туров PGA и LPGA.Вы можете увидеть расстояние для каждого клуба в процентах от расстояния водителя ниже: Расстояние до клуба в процентах от расстояния водителя. № 3. Вычислите расстояние идеального курса. Я произвольно определяю короткие, средние и длинные отверстия. Например, мое определение пар 5 средней длины — это драйвер, фервей №3 и качающийся клин. Я говорю, что пар 4 средней длины — это драйвер, а 6 — утюг. Нам нужно сделать это для каждой лунки; а именно решить, какие заходные выстрелы мы хотим попасть в каждую категорию лунок. Таким образом, чтобы вычислить расстояние пар пять средней длины относительно расстояния вашего водителя, математика выглядит так: Пар пятой средней длины Драйвер 1. # 3 Fairway .88 Pitching Wedge .45 Итого 2,33 Если ваш средний ход составляет 200, средняя дистанция по пар-5 составляет 466 ярдов. (2,33 х 200 ярдов). Выполните эту же логику для каждой лунки, и вы получите расстояние (расстояние водителя x 28) для идеальной длины поля. Драйвер x 28 Вычисление 4200 Вопросы по «Драйвер x 28»: 18
Декабрь 2018 18 декабря 2018 Информации о расчете объема Equal Tee меньше, но люди все еще хотят знать по многим причинам, например, по расчету вместимости воды. Здесь мы предоставим вам несколько простых методов расчета. Их легче вычислить, потому что их прямую форму можно рассматривать как прямые трубы, каким-то образом соединенные друг с другом. Так что вы можете рассчитать его объем как прямые трубы. Поэтому следует знать внутренний радиус равного тройника и его высоту (или длину) участка и ответвления.Затем вставьте значения в формулу объема для цилиндра и сложите результаты. Объем = пи (или 3,14) x радиус в квадрате x высота. Таким образом можно получить примерный объем тройника Если этот способ не подходит для вашей ситуации, возможно, лучший способ рассчитать объем — использовать воду и мерную емкость. Расчет Unequal Tee намного сложнее, поэтому вы можете выбрать этот метод. Иногда вам нужно знать объем, когда у вас есть только диаметр и график или давление. и сварной тройник (равный тройник ERW) являются тройниками под сварку встык, стандарт спецификации — ASME B16.9. У них большой диапазон размеров, поэтому перечислить все значения невозможно. Размер тройника для стыкового шва зависит только от их номинального размера. Вы можете быстро найти значение объема, но эта диаграмма не включает все номинальные размеры, поэтому вы можете не найти значение, которое хотите узнать. Тройник для стыковой сварки, объем Объем / м3 По размерам он больше похож на тройник с резьбой, хотя это фитинг под приварку, как тройник под сварку.Диапазон размеров составляет от 1/8 до 4 дюймов, а номинальное давление — Класс 3000, Класс 6000 и Класс 9000. Объем равнопроходного тройника для сварки внахлест зависит от этих двух факторов. В таблице объемов указан нормальный номинальный размер в диапазоне размеров и все номинальные значения давления, которые могут удовлетворить основные потребности пользователей. Тройник с резьбой и тройник для сварки внахлест — это поковки, которые соответствуют стандарту ASME B16. Более того, все объемы в таблице — это общий объем одного продукта и место, занимаемое при упаковке. Другими словами, это объемы фасованного продукта. Таблица размеров равного тройника по ASME B16.11 Как комитет турнира делает соревнования справедливыми, если игроки в гольф играют с разных наборов ти или мужчины играют с женщинами с одного набора ти? Важно с самого начала отметить, что гандикапы гольфа выравнивают игровое поле во время соревнований. Для того, чтобы соревнования игроков-ти с разными рейтингами поля были справедливыми, необходимо скорректировать гандикап поля игроков.
Повышение гандикапа для игроков, играющих с ти с более высоким рейтингом поля, или уменьшение гандикапа для игроков, играющих с
Могут применяться тройники с более низким рейтингом. Когда игроки в гольф соревнуются, играя с ти с разными рейтингами поля, либо прибавьте , либо вычтите ударов… В этом соревновании двух игроков Фред играет с синих ти, а Том играет с белых. В простой ситуации, когда у вас есть
двух игроков, USGA рекомендует скорректировать гандикап поля для игрока, играющего с ти, с более высоким рейтингом поля. В этом
В этом случае Фред играет из синих ти с более высоким рейтингом поля 71.3, поэтому вы должны добавить разницу в рейтинге курса (с округлением до
ближайшее целое число) к гандикапу Фреда, равному 12. Рейтинг синего поля — Рейтинг белого поля = разница в рейтинге поля  3.
3. Модуль упругости

Вокруг оси x
Радиус вращения
 2 \ over 4b} & \ quad, t_f \ gt {A \ over2 b} \ end {array} \ верно.3} {3}
2 \ over 4b} & \ quad, t_f \ gt {A \ over2 b} \ end {array} \ верно.3} {3} Связанные страницы
Как рассчитать объем равного тройника?
 Затем вставьте значения в формулу объема для цилиндра и сложите результаты.
Затем вставьте значения в формулу объема для цилиндра и сложите результаты. Номинальный размер Приблизительный объем / м3 DN NPS 15 1/2 0,037 * 10 -3 20 3/4 0,065 * 10 -3 25 1 0,138 * 10 -3 32 1 1/4 0. 279 * 10 -3
40 1 1/2 0,446 * 10 -3 50 2 0,726 * 10 -3 65 2 1/2 1,248 * 10 -3 80 3 1,994 * 10 -3 90 3 1/2 2,814 * 10 -3 100 4 3.892 * 10 -3 125 5 6,821 * 10 -3 150 6 0,011 200 8 0,022 250 10 0,042 300 12 0,068 350 14 0,091 400 16 0.126 450 18 0,179 500 20 0,245 550 22 0,327 600 24 0,388 350 26 0,539 700 28 0,649 750 30 0,8 800 32 0.  972
972 850 34 1,17 900 36 1,39 950 38 1,637 1000 40 1,913 1050 42 2.203 1100 44 2.401 1150 46 2,751 1200 48 3.137 1300 52 4,014 1400 56 4,952 1500 60 6.058  На диаграмме объема указаны нормальные номинальные размеры и различные номинальные значения давления в пределах диапазона размеров для удовлетворения основных потребностей пользователя.
На диаграмме объема указаны нормальные номинальные размеры и различные номинальные значения давления в пределах диапазона размеров для удовлетворения основных потребностей пользователя. Номинальный размер Приблизительный объем / м 3 DN NPS 3000 6000 9000 6 1/8 0.  03 * 10 -3
03 * 10 -3 0,04 * 10 -3 – 8 1/4 0,04 * 10 -3 0,04 * 10 -3 – 10 3/8 0,04 * 10 -3 0,06 * 10 -3 – 15 1/2 0,06 * 10 -3 0,20 * 10 -3 0,30 * 10 -3 20 3/4 0.20 * 10 -3 0,30 * 10 -3 0,46 * 10 -3 25 1 0,30 * 10 -3 0,46 * 10 -3 0,66 * 10 -3 32 1 1/4 0,46 * 10 -3 0,66 * 10 -3 1,09 * 10 -3 40 1 1/2 0,66 * 10 -3 1.  09 * 10 -3
09 * 10 -3 1,52 * 10 -3 50 2 1,09 * 10 -3 1,52 * 10 -3 2,52 * 10 -3 65 2 1/2 1,52 * 10 -3 2,35 * 10 -3 – 80 3 2,48 * 10 -3 3,62 * 10 -3 – 100 4 3.98 * 10 -3 – – В какие футболки лучше играть?

 Это более сложный вопрос, чем вы думаете, и большинство из нас переоценивают его как ключ к разгадке.Чтобы получить действительно точную оценку, вы можете использовать радары TrackMan в нашем ассортименте для измерения ваших приводов. Они точны с точностью до 1 фута на каждые 100 ярдов.
Это более сложный вопрос, чем вы думаете, и большинство из нас переоценивают его как ключ к разгадке.Чтобы получить действительно точную оценку, вы можете использовать радары TrackMan в нашем ассортименте для измерения ваших приводов. Они точны с точностью до 1 фута на каждые 100 ярдов.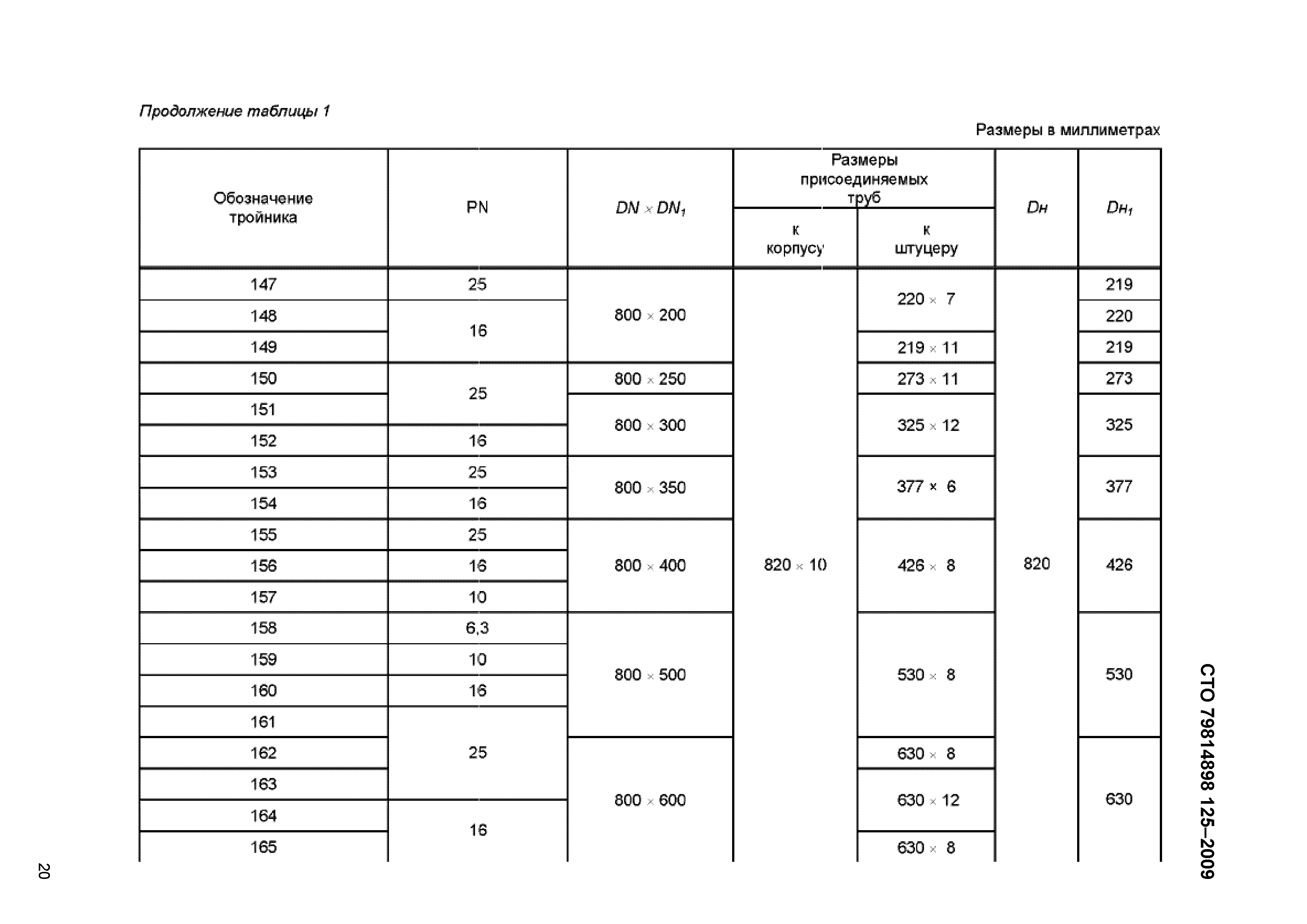
PGA Tour % из LPGA Tour % из Средние значения для тура драйвер водитель водитель 296 246 911 0. 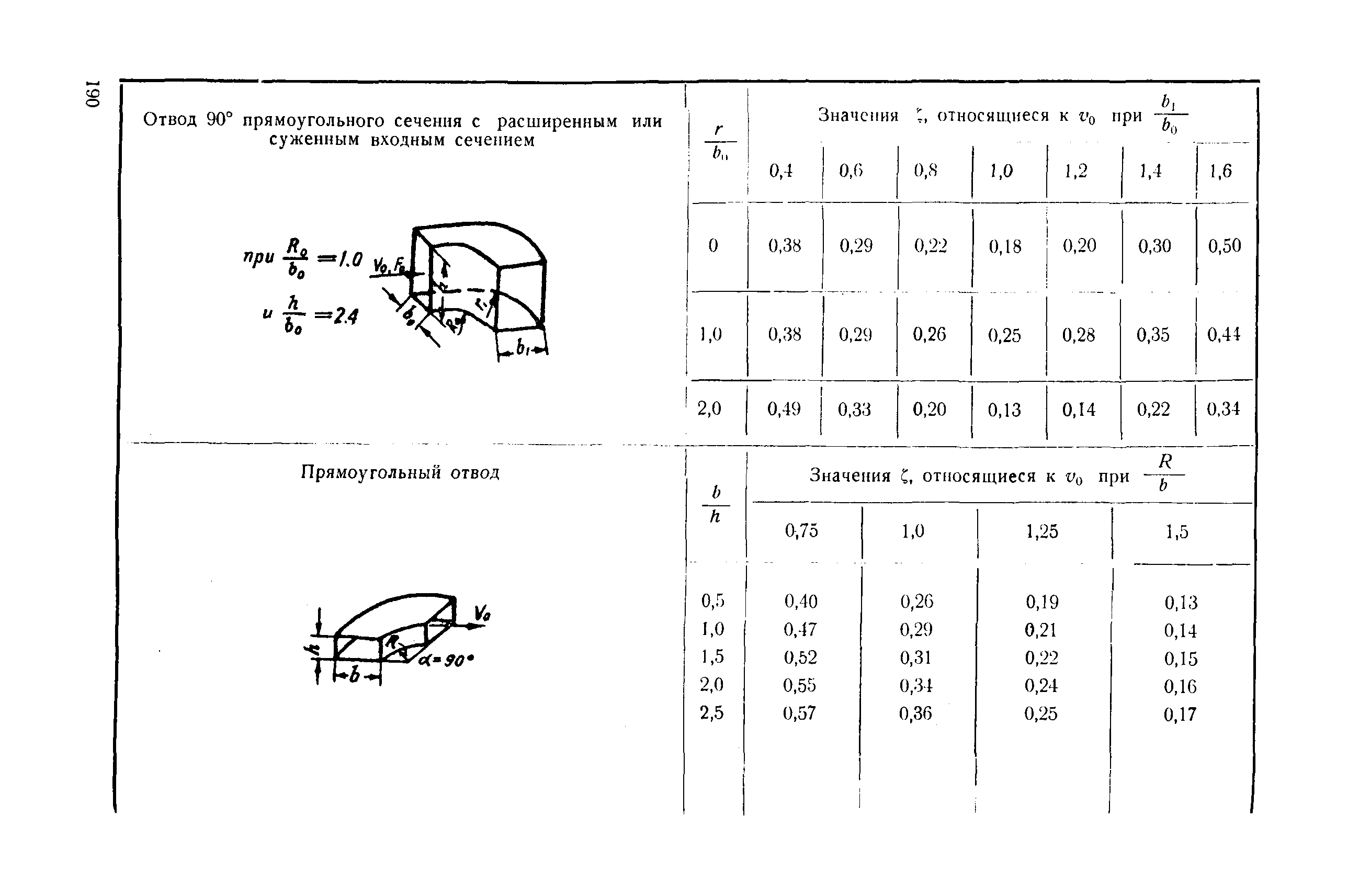 88
88 218 0,89 0,88 5w 242 0,82 200 0,81 0,82 7w1 911 911 911 911 911 911 911 0,76 hyb 237 0,80 0,80 3 220 0,74 0.74 4 209 0,71 180 0,73 0,72 5 198 0,67 170 0,69 185 0,63 159 0,65 0,64 7 177 0,60 147 0,60 0.  60
60 8 162 0,55 135 0,55 0,55 9 149 0,50 123 0,50 1 900 137 0,46 109 0,44 0,45 0
0Проектирование приятного поля для гольфа.
 Мое определение поля, на котором интересно играть, будет включать комбинацию коротких, средних и длинных лунок. Например, поскольку в среднем поле состоит из 4 лунок пар три, одна должна быть легкой, 2 — средней сложности и одна — сложной. Обычно имеется 4 паритета пятерки, поэтому та же логика применима к паритету 5. Обычно бывает 10 пар-четверок, поэтому я говорю, что есть 3 простых, 4 средних и 3 жестких пар-четверки. Это поле должно побудить вас поразить много разных клюшек, что обычно является определением хорошего поля для гольфа.
Мое определение поля, на котором интересно играть, будет включать комбинацию коротких, средних и длинных лунок. Например, поскольку в среднем поле состоит из 4 лунок пар три, одна должна быть легкой, 2 — средней сложности и одна — сложной. Обычно имеется 4 паритета пятерки, поэтому та же логика применима к паритету 5. Обычно бывает 10 пар-четверок, поэтому я говорю, что есть 3 простых, 4 средних и 3 жестких пар-четверки. Это поле должно побудить вас поразить много разных клюшек, что обычно является определением хорошего поля для гольфа. 00
00 Пар. Сложность Выбор клуба 900 # за раунд Итого% от драйвера 3 короткий 9 утюг 0. 
1 0,5 3 средний 6 железо 0,67 2 1,34 3 длинный 3 железо 0,74 4 короткий привод + 9 утюг 1,5 3 4,5 4 средний привод + 6 утюг 1.64 4 6,56 4 длинный водитель + 3 утюг 1,74 3 5,22 5 короткий водитель + 3 фарватера 1 1,88 5 средний водитель + 3 фервея + PW 2,37 2 4,74 5 длинный водитель + 3 фервэй + 6ir 2.  52
52 1 2,52 всего 18 28 900 Расстояние в пути 150 175 200 225 250 9005 Расстояние 4900 5600 6300 7000 7700  Если вы близки к 5%, это должно сработать. Кроме того, нет ничего плохого в том, чтобы составлять свой собственный курс. Ваш ход мне будет состоять из лунок с использованием разных тройников. Ваша цель должна заключаться в том, чтобы сыграть лунки, которые всегда дают вам возможность поразить каждый грин в соответствии с правилами (1 для пар-тройки, 2 для пар-четверок и 3 для пар-пятерок). Единственным недостатком составления собственного курса является то, что у вас не будет рейтинга курса для инвалидов.
Если вы близки к 5%, это должно сработать. Кроме того, нет ничего плохого в том, чтобы составлять свой собственный курс. Ваш ход мне будет состоять из лунок с использованием разных тройников. Ваша цель должна заключаться в том, чтобы сыграть лунки, которые всегда дают вам возможность поразить каждый грин в соответствии с правилами (1 для пар-тройки, 2 для пар-четверок и 3 для пар-пятерок). Единственным недостатком составления собственного курса является то, что у вас не будет рейтинга курса для инвалидов. Есть множество примеров игроков в гольф с высокими гандикапами, которые могут забить тонну. Им понравится играть по-настоящему короткий курс? То же самое и для гольфиста с низким гандикапом, который играет на короткой позиции.Будет ли ему или ей нравиться попадать в лес на фервее на большинстве пар четвер?
Есть множество примеров игроков в гольф с высокими гандикапами, которые могут забить тонну. Им понравится играть по-настоящему короткий курс? То же самое и для гольфиста с низким гандикапом, который играет на короткой позиции.Будет ли ему или ей нравиться попадать в лес на фервее на большинстве пар четвер?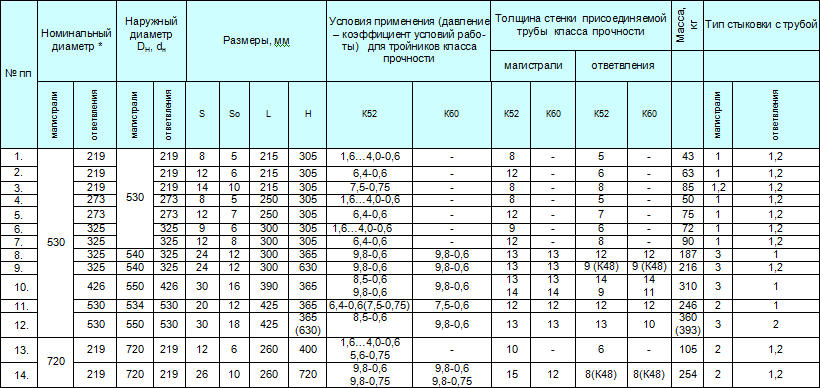 Это не так уж и плохо, потому что нападающий на 300 ярдов не будет очень часто ударить своего водителя, потому что он пройдет через собачью ногу или просто просто исчерпает пространство на фервее, чтобы ударить водителя.
Это не так уж и плохо, потому что нападающий на 300 ярдов не будет очень часто ударить своего водителя, потому что он пройдет через собачью ногу или просто просто исчерпает пространство на фервее, чтобы ударить водителя. Тройник равного объема | Поставщик качественных кованых фитингов-фланцев
 А если вам интересно, как рассчитать, вы можете прочитать следующую статью и найти свой идеальный метод.
А если вам интересно, как рассчитать, вы можете прочитать следующую статью и найти свой идеальный метод. Формула равного объема тройника
ASME B16.9 Тройник для стыковой сварки
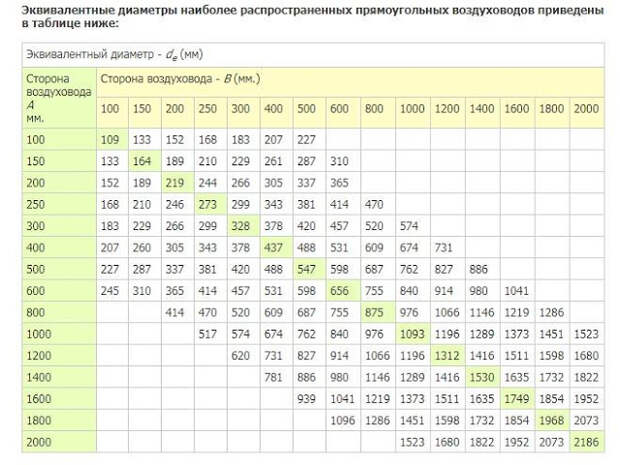 Что делать? К счастью, диаграмма объема может помочь вам решить проблему.
Что делать? К счастью, диаграмма объема может помочь вам решить проблему. Таблица объемов тройника под сварку встык
Номинальный размер Приблизительно DN NPS 15 1/2 0.037 * 10 -3 20 3/4 0,065 * 10 -3 25 1 0,138 * 10 -3 32 1 1/4 0,279 * 10 -3 40 1 1/2 0,446 * 10 -3 50 2 0,726 * 10 -3 65 2 1/2 1.  248 * 10 -3
248 * 10 -3 80 3 1,994 * 10 -3 90 3 1/2 2,814 * 10 -3 100 4 3.892 * 10 -3 125 5 6,821 * 10 -3 150 6 0,011 200 8 0.022 250 10 0,042 300 12 0,068 350 14 0,091 400 16 0,126 450 18 0,179 500 20 0,245 550 22 0,327 600 24 0.388 350 26 0,539 700 28 0,649 750 30 0,8 800 32 0,972 850 34 1,17 900 36 1,39 950 38 1,637 1000 40 1. 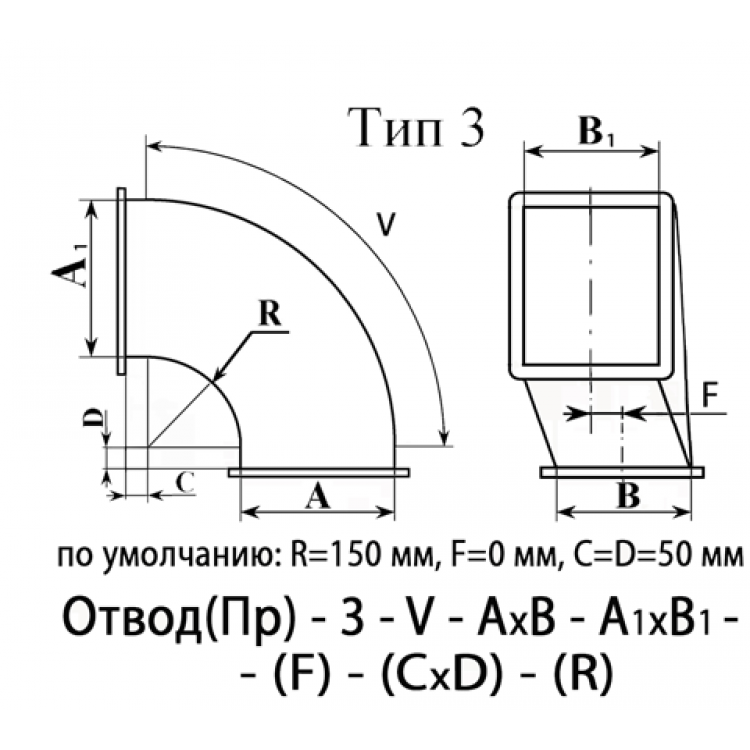 913
913 1050 42 2.203 1100 44 2.401 1150 46 2,751 1200 48 3,137 1300 52 4,014 1400 56 4,952 1500 60 6.058 Равный тройник для сварки внахлест
Тройник одинаковый с резьбой
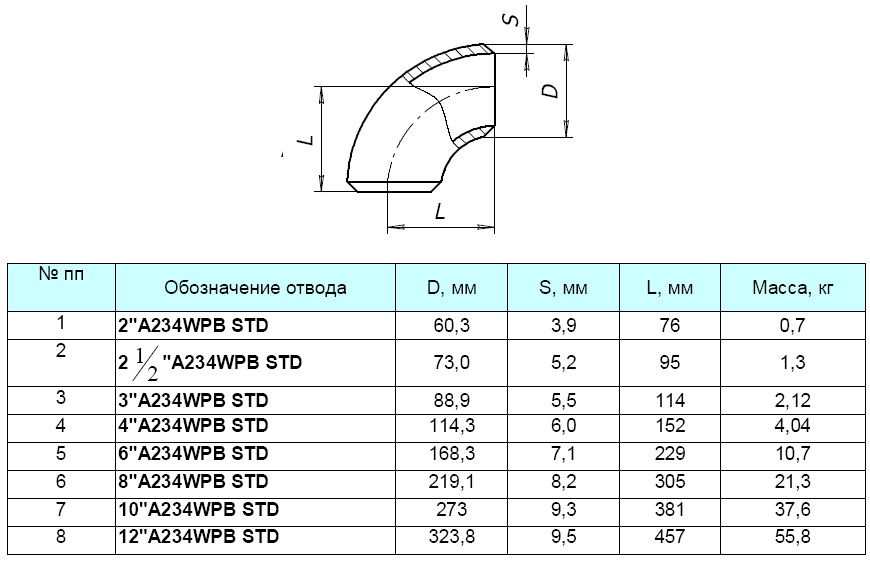 11 и имеют одинаковый диапазон размеров. Значит, их диаграмма объемов имеет одинаковые значения.
11 и имеют одинаковый диапазон размеров. Значит, их диаграмма объемов имеет одинаковые значения. Таблица размеров равного тройника ASME B16.11
Номинальный размер Приблизительный объем / м 3 DN NPS 3000 6000 9000 6 1/8 0.03 * 10 -3 0,04 * 10 -3 – 8 1/4 0,04 * 10 -3 0,04 * 10 -3 – 10 3/8 0,04 * 10 -3 0,06 * 10 -3 – 15 1/2 0,06 * 10 -3 0,20 * 10 -3 0,30 * 10 -3 20 3/4 0.  20 * 10 -3
20 * 10 -3 0,30 * 10 -3 0,46 * 10 -3 25 1 0,30 * 10 -3 0,46 * 10 -3 0,66 * 10 -3 32 1 1/4 0,46 * 10 -3 0,66 * 10 -3 1,09 * 10 -3 40 1 1/2 0,66 * 10 -3 1.09 * 10 -3 1,52 * 10 -3 50 2 1,09 * 10 -3 1,52 * 10 -3 2,52 * 10 -3 65 2 1/2 1,52 * 10 -3 2,35 * 10 -3 – 80 3 2,48 * 10 -3 3,62 * 10 -3 – 100 4 3.  98 * 10 -3
98 * 10 -3 – – Экспериментальный анализ напряжений для четырех 24-дюймовых. Стандарт ANSI B16. 9 тройников (конференция)
Hayes, JK, и Moore, S. E. Экспериментальный анализ напряжений для четырех 24-дюймовых. Стандарт ANSI B16. 9 тройников . США: Н. П., 1976.
Интернет. Хейс, Дж. К., и Мур, С. Э. Экспериментальный анализ напряжений для четырех 24-дюймовых. Стандарт ANSI B16. 9 тройников . Соединенные Штаты. Hayes, JK, и Moore, S.E. Thu.
«Экспериментальный анализ напряжений для четырех 24-дюймовых тройников стандарта ANSI B16.9». Соединенные Штаты. https://www.osti.gov/servlets/purl/7345907. @article {osti_7345907,
title = {Экспериментальный анализ напряжений для четырех 24-дюймовых.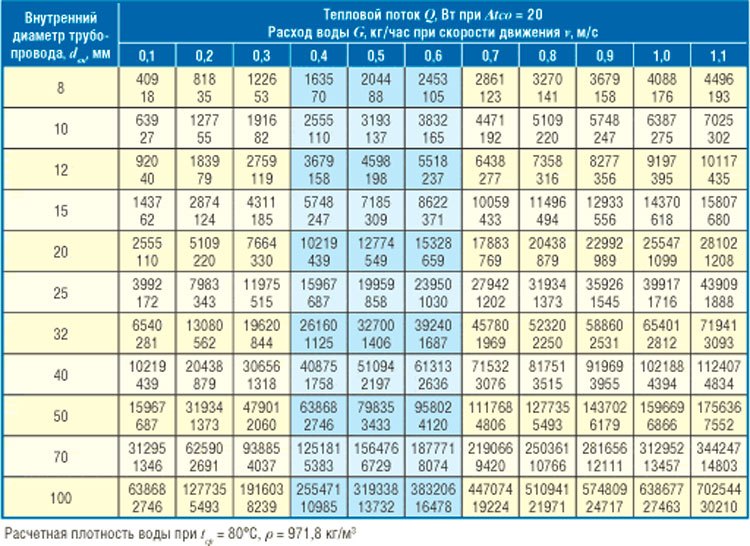 Стандарт ANSI B16. 9 тройников},
Стандарт ANSI B16. 9 тройников},
author = {Хейс, Дж. К. и Мур, С. Э.},
abstractNote = {Описываются экспериментальный анализ напряжений и испытания на малоцикловую усталость четырех тройников, испытанных Combustion Engineering, Inc. (E-E) по субподряду с Union Carbide Nuclear Division. Эти испытания являются частью программы ORNL «Критерии проектирования трубопроводов и форсунок», которая проводится для разработки критериев проектирования компонентов вспомогательных трубопроводов АЭС. Испытательные сборки были изготовлены на заводе C-E из коммерчески доступного стандарта ANSI B16.9 тройников и стальных труб соответствующего диаметра, приваренных к тройникам, с соответствующими затворами и приспособлениями для приложения нагрузок.},
doi = {},
url = {https://www.osti.gov/biblio/7345907},
journal = {},
number =,
объем =,
place = {United States},
год = {1976},
месяц = {1}
} Регулировка гандикапа — соревнование с разных ти
Разве гандикапы игроков не делают игру честной?
 от ОДИНАКОВЫХ тройников.Сравнение результатов с одной и той же футболки
аналогично сравнению яблок с яблок (если только это не смешанная конкуренция). А вот гандикапы в гольфе,
Не выравнивайте игровое поле, когда игроки играют в гольф с разных наборов ти или с одной футболки с разными
Рейтинги курсов (т.е. рейтинги мужчин и женщин). Сравнение результатов разных наборов футболок или разных рейтингов полей похоже на сравнение яблоки на апельсины .
от ОДИНАКОВЫХ тройников.Сравнение результатов с одной и той же футболки
аналогично сравнению яблок с яблок (если только это не смешанная конкуренция). А вот гандикапы в гольфе,
Не выравнивайте игровое поле, когда игроки играют в гольф с разных наборов ти или с одной футболки с разными
Рейтинги курсов (т.е. рейтинги мужчин и женщин). Сравнение результатов разных наборов футболок или разных рейтингов полей похоже на сравнение яблоки на апельсины . Честная игра

Практическое правило
Пример с двумя игроками
71,3 — 68,7 = 2,6 округляется до 3


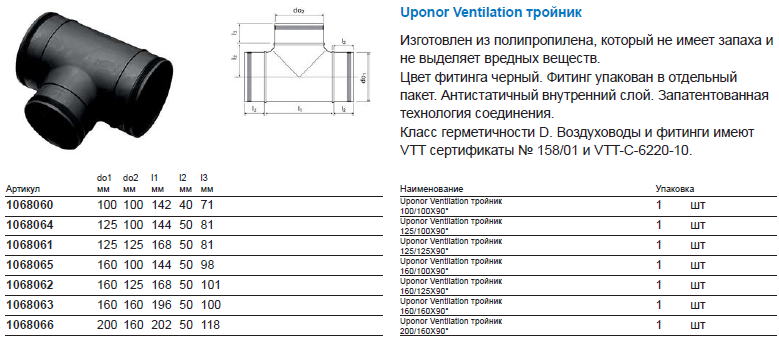

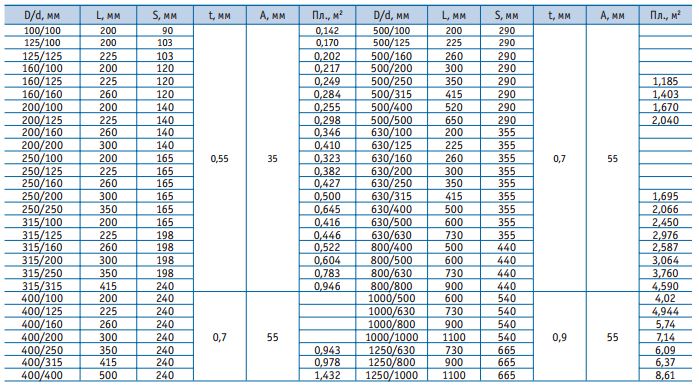

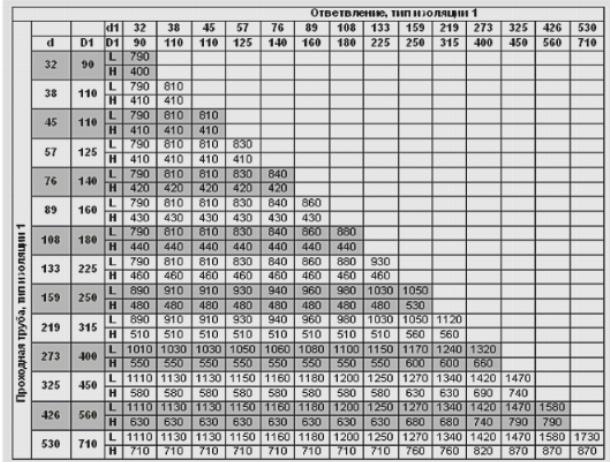

 Ранее подобная задача была решена автором применительно к сопротивлениям, встречающимся в водяных системах отопления [3]. Рассмотрим теперь данный вопрос для механических систем В и КВ. Ниже приведены результаты аппроксимации данных [2] для унифицированных тройников (узлов ответвлений) на проход. Общий вид зависимостей выбирался, исходя из физических соображений с учетом удобства пользования полученными выражениями при обеспечении допустимого отклонения от табличных данных:
Ранее подобная задача была решена автором применительно к сопротивлениям, встречающимся в водяных системах отопления [3]. Рассмотрим теперь данный вопрос для механических систем В и КВ. Ниже приведены результаты аппроксимации данных [2] для унифицированных тройников (узлов ответвлений) на проход. Общий вид зависимостей выбирался, исходя из физических соображений с учетом удобства пользования полученными выражениями при обеспечении допустимого отклонения от табличных данных: Кроме того, и для приточных, и для вытяжных тройников при изменении расхода воздуха в ответвлении относительный минимум КМС имеет место при одинаковом уровне Lo? = 0,2. Данные обстоятельства говорят о том, что полученные выражения, несмотря на свою простоту, в достаточной мере отражают общие физические закономерности, лежащие в основе влияния исследуемых параметров на потери давления в тройниках любого типа. В частности, чем больше fn? или fo?, т.е. чем ближе они к единице, тем меньше меняется структура потока при прохождении сопротивления, а значит, и меньше КМС. Для величины Lo? зависимость является более сложной, но и здесь она будет общей обоих режимов движения воздуха.
Кроме того, и для приточных, и для вытяжных тройников при изменении расхода воздуха в ответвлении относительный минимум КМС имеет место при одинаковом уровне Lo? = 0,2. Данные обстоятельства говорят о том, что полученные выражения, несмотря на свою простоту, в достаточной мере отражают общие физические закономерности, лежащие в основе влияния исследуемых параметров на потери давления в тройниках любого типа. В частности, чем больше fn? или fo?, т.е. чем ближе они к единице, тем меньше меняется структура потока при прохождении сопротивления, а значит, и меньше КМС. Для величины Lo? зависимость является более сложной, но и здесь она будет общей обоих режимов движения воздуха. 22.38 с помощью формулы (3). Заметим, что, хотя в последнем случае речь идет о круглом сечении, нетрудно убедиться, что выражение (3) достаточно удачно описывает и данные табл. 22.39, относящиеся уже к прямоугольным узлам.
22.38 с помощью формулы (3). Заметим, что, хотя в последнем случае речь идет о круглом сечении, нетрудно убедиться, что выражение (3) достаточно удачно описывает и данные табл. 22.39, относящиеся уже к прямоугольным узлам. Их применение позволяет отказаться от интерполяции таблиц при сохранении точности, требуемой для инженерных расчетов, и непосредственно вычислять КМС тройников на проход при самых разнообразных соотношениях сечений и расходов воздуха в стволе и ответвлениях. Этого вполне достаточно для проектирования систем В и КВ в большинстве жилых и общественных зданий.
Их применение позволяет отказаться от интерполяции таблиц при сохранении точности, требуемой для инженерных расчетов, и непосредственно вычислять КМС тройников на проход при самых разнообразных соотношениях сечений и расходов воздуха в стволе и ответвлениях. Этого вполне достаточно для проектирования систем В и КВ в большинстве жилых и общественных зданий.