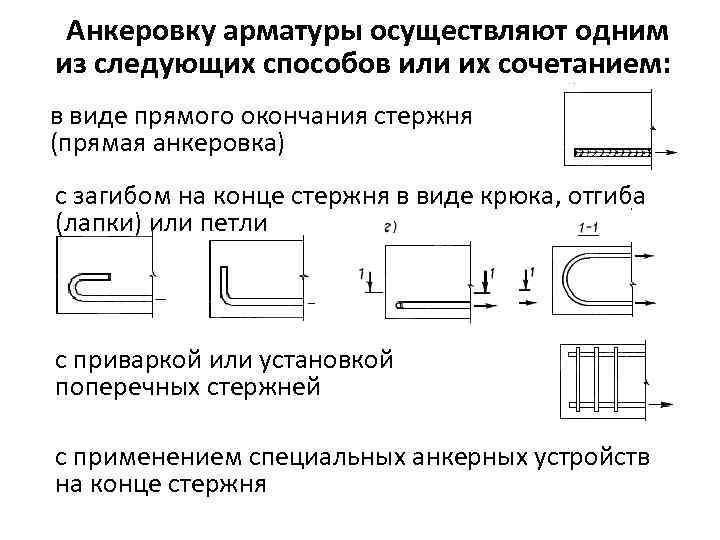
Сравнение расчетов сборных элементов каркаса железобетонного здания по нормам СП 63.13330 и Еврокоду 2
Авторы: Тимофеев Павел Сергеевич, Митасов Валерий Михайлович
Рубрика: Архитектура, дизайн и строительство
Опубликовано в Молодой учёный №14 (304) апрель 2020 г.
Дата публикации: 06.04.2020 2020-04-06
Статья просмотрена: 710 раз
Скачать электронную версию
Скачать Часть 2 (pdf)
Библиографическое описание: Тимофеев, П.
В статье приведен анализ сравнительного расчета железобетонных элементов каркаса жилого здания, выполненных по единым нормам Евросоюза — Eurocode 2 и актуальным нормам РФ — СП63.13330. За расчетный элемент принят сборный железобетонный ригель 300х400, Рассчитанный на прочность и эксплуатационную жесткой по вышеобозначенным нормам. В статье рассматривается не сам расчет, а его результаты.
Ключевые слова: нормы проектирования, Eurocode, Сравнительный анализ расчетов.
The article provides an analysis of the comparative calculation of reinforced concrete frame elements of a residential building, made according to the unified standards of the European Union — Eurocode 2 and the current standards of the Russian Federation — SP63.
Keywords: design standards, Eurocode, Comparative analysis of calculations.
Исторически при образовании единого европейского пространства, была начата работа по, сначала, стандартизации, а после и созданию единых стандартов строительства. В начале девяностых годов прошлого века были созданы первые единые нормы строительства — EN1990 и EN1991, лежащих в основе современных Eurocode, использующихся в странах союза, а так же принятые в странах, сотрудничающих с ними — Турция, Белоруссия (официально, как основные нормы), Украина (как возможная альтернатива современным принятым в стране).
Современный свод правил (СП 63.13330) создан в 2012 на базе СП 52, который в свою очередь основан на ещё советских нормах СНиП 2.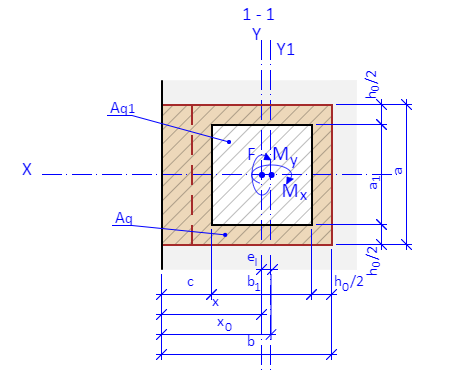 01.03.1984 и с использованием некоторых расчетных моделей из EN1991.
01.03.1984 и с использованием некоторых расчетных моделей из EN1991.
Современные нормы строительства Европы и России очень сильно отличаются ещё на моменте создания математических моделей, описывающих формулы, принятые в этих нормах.
1. Математическое сравнение норм проектирования
Если более подробно рассматривать нормы, то первым отличием является различные коэффициенты запаса по материалу и прочности, принятые в нормах: Eurocode предлагает застраховать упрощение математических моделей реальных конструкций, путем введения дополнительных коэффициентов запаса «по неточности модели» yt.
СП же предлагает рассматривать запас конструкций с учётом нормального распределения Гаусса, и вводит коэффициенты запаса, ограничивающие возможность большого отклонения от проектных значений нагрузок и сопротивления материалов внешнему воздействию. Этот пункт будет рассмотрен в работе ниже.
Так же отличительной особенностью Eurocode является нестандартные модели расчета на поперечную силу и прогиб, которые, в отличие от СП, имеют сильнейшее расхождение с реальным поведением конструкций в каждом из рассчитываемых прочностных характеристик сечения.
2. Описание рассчитываемого элемента
Рассчитывался ригель длинной 6м шарнирно опертый на консоли колонн для многоэтажного здания. Здания 10 этажное 36м х 24м в плане, грузовая площадь ригеля составляет 6м.
Расчет проходил в 2 этапа для каждой из норм проектирования: первым этапом был сбор нагрузок на перекрытие и ригель, вторым этапом был непосредственно расчет по первой и второй групамм предельных состаяний.
В результате расчета по СП 63.13330 поперечная арматура была принята конструктивно, исходя из расчета на поперечную силу, прогиб не превышал допустимые пределы.
Таблица 1
Изгибающий момент всередине пролета | Поперечная сила | Ширина раскрытия трещин | Прогиб ригеля | ||
Продолжит. | Непродолжит. | ||||
Ригель СП 63.13330 | М = 334,71кНм | Q = 228 кН | acrc= 0,200 мм | acrc1= 0,228 мм | f = 15,493 мм |
Ригель Eurocode 2 | МEd 431,71 кНм | VEd 287,95 кН | wk= 0,16 мм wmax = 0,4 мм | a = 23 мм | |
По Eurocode 2 расчет на поперечную силу потребовал введение поперечной арматуры 4 х d = 14мм, прогиб практически равен максимальному.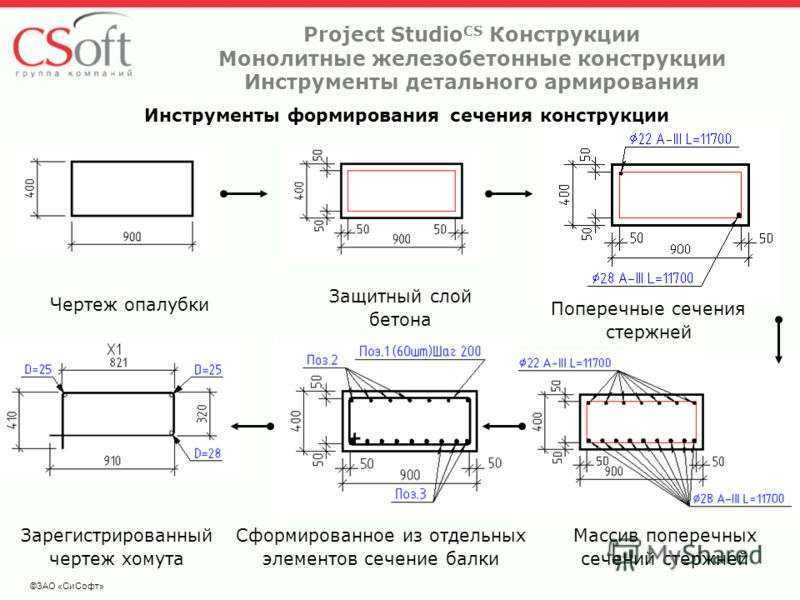
3. Анализ исравнение расчета по разным нормам проектирования
Исходя из предыдущих расчетов можем составить сводную таблицу, со сравнением результатов расчета по предложенным нормам по Eurocode 2 требует большей материалоемкости при тех же первоначальных нагрузках.
Таблица 2
Внешние воздействия ижесткостные характеристики ригеля
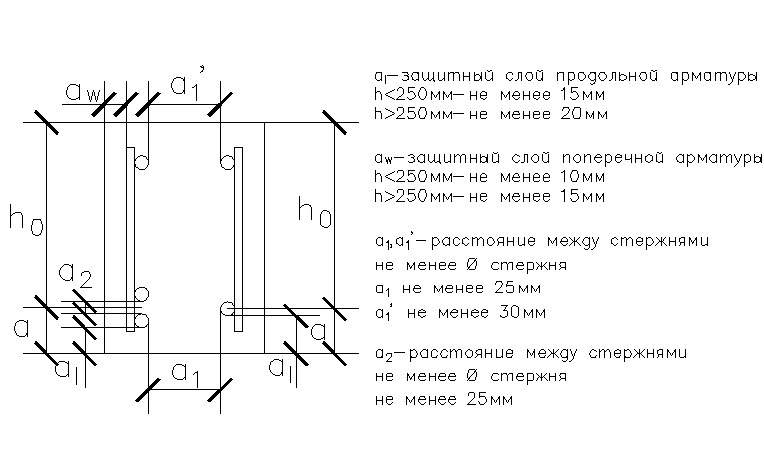
Рабочая высота сечения | Площадь продольной растянутой арматуры | Площадь продольной сжатой арматуры | Площадь поперечной арматуры | Арматура на подрезках | |
Ригель | 350 мм | Аs = 3217мм2 (4⌀32) | A’s = 157 мм2(2⌀10) | Asw = 20,1 мм2 (4⌀8)Sw =100 | Аs=1232 мм2 (2⌀28) |
Ригель Eurocode 2 | 342 мм | Аs = 4021 мм2 (4⌀36) | Аs1= 402 мм2 (2⌀16) | 4⌀14 Asw = 61,6 мм2 Sw = 150 | 2⌀32 Аs=1608 мм2 |
Отношение рассчитанных внутренних усилий, воспринимаемых единицей площади арматуры приведены на Рис. 1.
1.
Рис. 1
Рис. 2
Как видно из графиков расчет ригеля по нормам Eurocode требует на 4 % больше армирования из расчета на действие изгибающего момента, чем аналогичный расчет, выполненный по нормам СП 63.13330.
На Рис.3.расчетные величины и полученных значений при расчете по предельным состояниям второй группы составлены графики
Рис. 3
Рис. 4
Как видим из рисунка 4, несмотря на большую обеспеченность 60 % по Eurocode ширины раскрытия трещин против 43 % по СП 63.13330, расчет прогиба по европейским нормам практически не оставляет запаса жесткости по 2 группе предельных состояний.
Но если принять во внимание, уже учтенные из-за неточности модели коэффициенты запаса по нагрузке, показателю прочности бетона и арматуры в Eurocode, то мы получаем искаженные данные прогиба для ригеля загруженного так же, как и в случае расчета по СП 63.13330 нагрузкой собранный выше. Этот перерасход определяется, как отношение начальной нагрузки на элемент из таблицы сбора нагрузок q n1, к полученной принятой арматурой для расчета по I группе предельных состояний, и той же той же начальной нагрузкой qn1 к рассчитанному прогибу элемента, для II группы предельных состояний. Эти отношения приведены на рисунке 5.
Эти отношения приведены на рисунке 5.
Рис. 5
Как видно из этих диаграмм, прогиб, посчитанный по Eurocode, превышает прогиб, посчитанный по СП 63.13330 на 48 %.
4. Основные выводы
Из-за несовершенства математической модели, далекой от реального поведения строительного материала, при расчетах по Еврокоду 2 мы сталкиваемся с большим количеством проблем:
Перерасход материала. Речь идет не об увеличении материалоемкости, т. к. превышение расчетных усилий над аналогичными, им рассчитанными по нормам СП, исчисляется процентами и составляет 10–25 % относительно аналогичных по СП [п. 2.3]. В то время, как увеличение необходимого армирования превосходит рассчитанное по нормам сп уже в порядковом значении. Разница в 1 диаметр на каждом из этапов расчета является превышением второго порядка, исходя из простейшей геометрии.
Несоответствие деформаций, рассчитанных с применением математических моделей из еврокодов, реальным деформациям. Это проистекает из-за введения дополнительных коэффициентов запаса, которые, как и в случае с расчетом на прочность появляются из-за несовершенства модели. В то время, как вторая группа предельных состояний по современным российским нормам основывается интеграле мора, являясь его упрощенной моделью, расчет прогиба по еврокодам происходит из малоизученного момента появления первой стохастической трещины и дальнейшим ее поведении. В итоге математическая модель расчета по эксплуатационным характеристикам построена на базе эмпирических наблюдений и нуждается в введении повышенных коэффициентов запаса, что на фоне увеличенных внутренних усилий и показывает чрезмерные деформации, несоответствующие реальным.
Это проистекает из-за введения дополнительных коэффициентов запаса, которые, как и в случае с расчетом на прочность появляются из-за несовершенства модели. В то время, как вторая группа предельных состояний по современным российским нормам основывается интеграле мора, являясь его упрощенной моделью, расчет прогиба по еврокодам происходит из малоизученного момента появления первой стохастической трещины и дальнейшим ее поведении. В итоге математическая модель расчета по эксплуатационным характеристикам построена на базе эмпирических наблюдений и нуждается в введении повышенных коэффициентов запаса, что на фоне увеличенных внутренних усилий и показывает чрезмерные деформации, несоответствующие реальным.
Литература:
- СП 63.13330.2012
- Eurocode 2
- TKP EN-1991
- CEN/TC250 — Erocodes
- «Вероятностные основы расчета строительных конструкций» Краснощеков изд. СибАДИ 2016 г.
- «Расчет строительных конструкций, сочетания нагрузок» dystlab.
 com
com - «Руководство для проектировщиков к Еврокоду 2» Э. В. Биби, Р. С. Нараянан изд. МГАСУ 2015 г.
- «Проектирование железобетонных конструкций» Справочное пособие А. Б. Голышев 1985 г.
- НИИРС «Сравнение главных балок железобетонного перекрытия» В. В. Роот 2015 г.
- «Worked Examples for Eurocode 2» Concrete Centre 2017 г.
- Расчет железобетонных конструкций по еврокоду EN 1992 С. К. Яковлев, Я. И. Мысляева изд. МГАСУ
- «Reliability of structural members designed with the Eurocodes NDPs selected by EU and EFTA Member States» J. Markova, M. L. Sousa, S. Dimova, A. Athanasopoulou, S. Iannaccone 2018 г.
Основные термины (генерируются автоматически): поперечная сила, расчет, норма, норма проектирования, норма сп, поперечная арматура, дополнительный коэффициент запаса, коэффициент запаса, начальная нагрузка, расчет прогиба.
Ключевые слова
нормы проектирования, Eurocode, Сравнительный анализ расчетовнормы проектирования, Eurocode, Сравнительный анализ расчетов
Похожие статьи
Сравнительный анализ методов
расчета длины анкеровки. ..
..Метод расчета по СП 63.13330.2012 «Бетонные и железобетонные конструкции.
Метод расчета по ТКП EN 1992–1–1–2009 «Проектирование железобетонных конструкций.
α4 — коэффициент для учета влияния одного или нескольких приваренных поперечных стержней…
Сравнение общих положений
расчета стальных конструкций по…Основные термины (генерируются автоматически): расчет, конструкция, норма, расчет элементов
Нормы проектирования предопределяют необходимость учета всех факторов, влияющих на
Таким образом, в расчете учитывают то, что возможность начального отказа…
Анализ несущей способности лестничного марша при
нагрузках. ..
..Коэффициент 1,1 принят в соответствие с таблицей 7.1 СП 20.13330.2011 «Нагрузки и воздействия». Тогда общий вес всех элементов будет составлять
Проведем расчет максимальной несущей способности марша на общий изгибающий момент. Коэффициент
Расчет надежности железобетонных элементов конструкцийОсновное требование к расчету надежности конструкции — это обеспечение ее прочности при
Произведем расчет надежности для элемента конструкции, одного из наиболее часто
где — коэффициент вариации прочности бетона, и — математическое ожидание и среднее…
Использование нормативной литературы при
проектировании…Если при проектировании конструкций пользоваться современными нормами [4], то ширину
− расчет конструкций при отсутствии и наличии предварительного напряжения арматуры. ..
..
Если принять в расчете не расчетное сопротивление арматуры по площадке текучести, а по…
Совершенствование методики
расчёта пологих железобетонных…Данная статья посвящена особенностям расчёта пологих железобетонных сводов, опирающихся на металлические балки. В ней приведены основные причины ошибок при проектировании подобных конструкций, ведущие, в дальнейшем…
Расчёт стержня с распределенными продольными связямиПолучить выражения для перемещений и продольных сил; коэффициент температурного расширения .
Применение описанных выше методик расчёта и методов совершенствования конструкций может существенно помочь проектировщикам на стадии проектирования и как…
Расчет сечения сборно-монолитной конструкции в стадии. ..
..За расчетную поперечную силу принята. Расчет прочности нормального сечения при действии изгибающего момента. Проверим условие.
Поперечная арматура ригеля класса А500С (Rsw = 300 МПа, Es=20000 МПа), в одном поперечном сечении 48 (Asw=201мм2) с шагом s=100 мм.
Обследование строительных конструкций зданий по хранению…
Поперечная сила от суммарной распределенной нагрузки. 0,101. Максимальный прогиб в центре плиты. 5,35*10–005. Коэффициент использования 0,561 — Изгибающий момент от суммарной распределенной нагрузки. Коэффициент надежности по ответственности 1.
Похожие статьи
Сравнительный анализ методов
расчета длины анкеровки…Метод расчета по СП 63. 13330.2012 «Бетонные и железобетонные конструкции.
13330.2012 «Бетонные и железобетонные конструкции.
Метод расчета по ТКП EN 1992–1–1–2009 «Проектирование железобетонных конструкций.
α4 — коэффициент для учета влияния одного или нескольких приваренных поперечных стержней…
Сравнение общих положений
расчета стальных конструкций по…Основные термины (генерируются автоматически): расчет, конструкция, норма, расчет элементов
Нормы проектирования предопределяют необходимость учета всех факторов, влияющих на
Таким образом, в расчете учитывают то, что возможность начального отказа…
Анализ несущей способности лестничного марша при
нагрузках…Коэффициент 1,1 принят в соответствие с таблицей 7. 1 СП 20.13330.2011 «Нагрузки и воздействия». Тогда общий вес всех элементов будет составлять
1 СП 20.13330.2011 «Нагрузки и воздействия». Тогда общий вес всех элементов будет составлять
Проведем расчет максимальной несущей способности марша на общий изгибающий момент. Коэффициент
Расчет надежности железобетонных элементов конструкцийОсновное требование к расчету надежности конструкции — это обеспечение ее прочности при
Произведем расчет надежности для элемента конструкции, одного из наиболее часто
где — коэффициент вариации прочности бетона, и — математическое ожидание и среднее…
Использование нормативной литературы при
проектировании…Если при проектировании конструкций пользоваться современными нормами [4], то ширину
− расчет конструкций при отсутствии и наличии предварительного напряжения арматуры.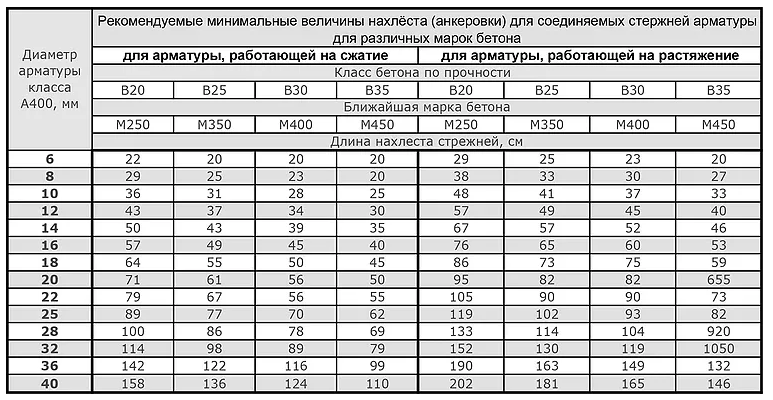 ..
..
Если принять в расчете не расчетное сопротивление арматуры по площадке текучести, а по…
Совершенствование методики
расчёта пологих железобетонных…Данная статья посвящена особенностям расчёта пологих железобетонных сводов, опирающихся на металлические балки. В ней приведены основные причины ошибок при проектировании подобных конструкций, ведущие, в дальнейшем…
Расчёт стержня с распределенными продольными связямиПолучить выражения для перемещений и продольных сил; коэффициент температурного расширения .
Применение описанных выше методик расчёта и методов совершенствования конструкций может существенно помочь проектировщикам на стадии проектирования и как…
Расчет сечения сборно-монолитной конструкции в стадии. ..
..За расчетную поперечную силу принята. Расчет прочности нормального сечения при действии изгибающего момента. Проверим условие.
Поперечная арматура ригеля класса А500С (Rsw = 300 МПа, Es=20000 МПа), в одном поперечном сечении 48 (Asw=201мм2) с шагом s=100 мм.
Обследование строительных конструкций зданий по хранению…
Поперечная сила от суммарной распределенной нагрузки. 0,101. Максимальный прогиб в центре плиты. 5,35*10–005. Коэффициент использования 0,561 — Изгибающий момент от суммарной распределенной нагрузки. Коэффициент надежности по ответственности 1.
Расчет прогибов ЖБК в соответствии нормами СП 63.13330.ХХХХ
Теги: #ЛИРА-САПР #ЖБК #прогибы #нелинейность
Ниже описываются требования норм к расчету прогибов железобетонных элементов и их реализация в ПК ЛИРА-САПР.
Расчет прогибов в соответствии с СП 63.13330.ХХХХ определяется на основании кривизны железобетонного элемента.
8.2.24 Полную кривизну изгибаемых, внецентренно сжатых и внецентренно растянутых элементов определяют по формулам:
— для участков без трещин в растянутой зоне:
1/r=(1/r)1+(1/r)2 (8.140)
— для участков с трещинами в растянутой зоне:
1/r=(1/r)1-(1/r)2+(1/r)3 (8.141)
В формуле (8.140):
(1/r)1, (1/r)2 – кривизны соответственно от непродолжительного действия кратковременных нагрузок и от продолжительного действия постоянных и временных длительных нагрузок.
В формуле (8.141):
(1/r)1 – кривизна от непродолжительного действия всей нагрузки, на которую производят расчет по деформациям;
(1/r)2 – кривизна от непродолжительного действия постоянных и временных длительных нагрузок;
(1/r)3 – кривизна от продолжительного действия постоянных и временных длительных нагрузок.
Кривизна железобетонного элемента определяется в зависимости от его изгибной жесткости D, которая зависит от модуля деформаций бетона Eb1 и приведенного момента инерции сечения Ired.
Изгибная жесткость D элемента определяется с учетом того, образовались или нет на данном участке нормальные трещины.
8.2.25 Кривизну железобетонных элементов 1/r от действия соответствующих нагрузок (см. 8.2.24) определяют по формуле
1/r=M/D, (8.142)
где М – изгибающий момент от внешней нагрузки (с учетом момента от продольной силы N) относительно оси, нормальной плоскости действия изгибающего момента и проходящей через центр тяжести приведенного поперечного сечения элемента;
D – изгибная жесткость приведенного поперечного сечения элемента, определяемая по формуле
D=Eb1*Ired, (8.143)
где Eb1 – модуль деформации сжатого бетона, определяемый в зависимости от продолжительности действия нагрузки и с учетом наличия или отсутствия трещин;
Ired – момент инерции приведенного поперечного сечения относительно его центра тяжести, определяемый с учетом наличия или отсутствия трещин.
Значения модуля деформации бетона Еb1 и момента инерции приведенного сечения Ired для элементов без трещин в растянутой зоне и с трещинами определяют по 8.2.26 и 8.2.27 соответственно.
Значения модуля деформации бетона в формулах (8.143), (8.145) принимают равными:
– при непродолжительном действии нагрузки
Eb1=0.85Eb, (8.146)
– при продолжительном действии нагрузки
Eb1=Ebτ=Eb1/(1+φb,cr) (8.147)
где φb,cr принимают по таблице 6.12.
ПК ЛИРА-САПР при определении прогибов элементов оперирует их жесткостью. При таком подходе полученные прогибы следует суммировать аналогично кривизне
8.2.31 Прогибы железобетонных элементов можно определять по общим правилам строительной механики с использованием вместо кривизны 1/r непосредственно изгибных жесткостных характеристик D путем замены упругих изгибных характеристик EI в расчетных зависимостях на характеристики D, вычисляемые по формулам, приведенным в 8. 2.25 и 8.2.29.
2.25 и 8.2.29.
При совместном действии кратковременной и длительной нагрузок полный прогиб элементов без трещин и с трещинами в растянутой зоне определяют путем суммирования прогибов от соответствующих нагрузок по аналогии с суммированием кривизны по 8.2.24, принимая жесткостные характеристики D в зависимости от указанной в этом пункте принятой продолжительности действия рассматриваемой нагрузки.
Допускается при определении жесткостных характеристик D элементов с трещинами в растянутой зоне принимать коэффициент ψs= 1. В этом случае при совместном действии кратковременной и длительной нагрузок полный прогиб изгибаемых элементов с трещинами определяют путем суммирования прогибов от непродолжительного действия кратковременной нагрузки и от продолжительного действия длительной нагрузки с учетом соответствующих значений жесткостных характеристик D, т. е. подобно тому, как это принято для элементов без трещин.
Пример.
Прямоугольный свободно опертый элемент пролетом 4800мм. Бетон класса В15, арматура – А500. Размеры сечения: b=300мм h=600мм, a=a’=40мм. Продольная арматура 4d32. На элемент действует равномерно распределенная нагрузка – длительная 75кН/м и кратковременная 15кН/м. Кроме того приложена продольная растягивающая сила – длительная 16кН и кратковременная 10кН. Влажность воздуха лежит в диапазоне 40-75%.
Бетон класса В15, арматура – А500. Размеры сечения: b=300мм h=600мм, a=a’=40мм. Продольная арматура 4d32. На элемент действует равномерно распределенная нагрузка – длительная 75кН/м и кратковременная 15кН/м. Кроме того приложена продольная растягивающая сила – длительная 16кН и кратковременная 10кН. Влажность воздуха лежит в диапазоне 40-75%.
Расчет ведем в физически нелинейной постановке.
Для описания диаграммы σ-ε применяем 14й закон деформирования – трехлинейную диаграмму деформирования для бетона и двухлинейную для арматурной стали. Т.к. работа материала описывается диаграммой σ-ε, а не модулем деформаций, то влияние кратковременной и длительной ползучести реализовывается путем умножение значений относительных деформаций бетона εb1 и εbt1 на коэффициенты 1/0.85=1.176 и 1+φb,cr=1+3.4=4.4 соответственно. Такой подход аналогичен, по своей сути, формулам (8.146) и (8.147).
Относительные деформации εb0 ,εb2, εbt0, εbt2 принимаются в зависимости от длительности действия нагрузок: εb0=-0. 002, εb2=-0.0035, εbt0=0.0001, εbt2=0.00015 при кратковременном действии нагрузок, εb0=-0.0034, εb2=-0.0048, εbt0=0.00024, εbt2=0.00031 при длительном действии нагрузок (таблица 6.10 СП 63).
002, εb2=-0.0035, εbt0=0.0001, εbt2=0.00015 при кратковременном действии нагрузок, εb0=-0.0034, εb2=-0.0048, εbt0=0.00024, εbt2=0.00031 при длительном действии нагрузок (таблица 6.10 СП 63).
На участках с трещинами принимается диаграмма работы бетона без учета растянутой ветви.
Исходная диаграмма σ-ε бетона класса В15
| ε | σ,тс/м2 |
| -0.003500 | -1122.00 |
| -0.002000 | -1121.00 |
| -0.000275 | -673.20 |
| 0.000000 | 0.00 |
| 0.000028 | 67.32 |
| 0.000100 | 111.00 |
| 0.000150 | 112.20 |
Диаграмма σ-ε бетона класса В15 с учетом кратковременной ползучести
| ε | σ,тс/м2 |
-0. 003500 003500 |
-1122.00 |
| -0.002000 | -1121.00 |
| -0.000324 | -673.20 |
| 0.000000 | 0.00 |
| 0.000033 | 67.32 |
| 0.000100 | 111.00 |
| 0.000150 | 112.20 |
Диаграмма σ-ε бетона класса В15 с учетом длительной ползучести
| ε | σ,тс/м2 |
| -0.0048 | -1122.00 |
| -0.0034 | -1121.00 |
| -0.001210 | -673.20 |
| 0.000000 | 0.00 |
| 0.000123 | 67.32 |
| 0.00024 | 111.00 |
| 0.00031 | 112.20 |
Диаграмма σ-ε арматуры класса А500
| ε | σ,тс/м2 |
-0. 025 025 |
-51000 |
| -0.0025 | -50999 |
| 0 | 0 |
| 0.0025 | 50999 |
| 0.025 | 51000 |
Момент инерции сечения Ired определяется автоматически в зависимости от полученного во время расчета НДС нормального сечения.
Таким образом, во время физически нелинейного расчета ПК ЛИРА-САПР определяет жесткостные характеристики элементов автоматически.
По длине балки назначается 2 типа жесткости – с учетом работы растянутой ветви (для участков без трещин) и без этого учета (на участках с трещинами).
Типы жесткости:
1 – диаграмма σ-ε с учетом длительной ползучести и учетом растянутой ветви работы бетона;
2 – диаграмма σ-ε с учетом кратковременной ползучести и учетом растянутой ветви работы бетона;
3 – диаграмма σ-ε с учетом длительной ползучести, без учета растянутой ветви работы бетона;
4 – диаграмма σ-ε с учетом кратковременной ползучести, без учета растянутой ветви работы бетона.
Нагрузки прикладываем в 2х загружениях: загружение 1 – длительные нагрузки, загружение 2 – кратковременные.
Для получения трех составляющих прогибов f1, f2, f3 создаем 3 балки:
балка 1 – характеристики жесткости, соответствующие кратковременной ползучести; нагрузка 75кН/м в загружении 1 и 15кН/м в загружении 2;
балка 2 – характеристики жесткости, соответствующие кратковременной ползучести; нагрузка 75кН/м в загружении 1;
балка 3 – характеристики жесткости, соответствующие длительной ползучести; нагрузка 75кН/м в загружении 1.
Рисунок 1. Длительные нагрузки (загружение 1) с мозаикой жесткостей
Рисунок 2. Кратковременные нагрузки (загружение 2) с мозаикой жесткостей
Рисунок 3. Принятые диаграммы σ-ε бетона соответственно для типов жесткости 1-4 (слева на право)
Рисунок 4. Принятая диаграмма σ-ε арматуры
Рисунок 5. Армирование сечения (используется ТЗА)
Для выполнения нелинейного расчета следует задать шаговую историю нагружения:
Результаты расчета:
Рисунок 6. Сверху вниз: эпюры прогибов от непродолжительного действия полных нагрузок f1, непродолжительного действия постоянных и временных длительных f2, продолжительного действия постоянных т временных длительных f3
Сверху вниз: эпюры прогибов от непродолжительного действия полных нагрузок f1, непродолжительного действия постоянных и временных длительных f2, продолжительного действия постоянных т временных длительных f3
Прогиб балки составляет:
f=f1-f2+f3=10.1-8.23+9.68=11.55мм
Суперпозиция по СП 20.13330.2016: Нагрузки и воздействия
НаверхПереключить боковую панель оглавления
Введение
Этот документ представляет собой краткое введение в использование программы MAXIMA для комбинаций в соответствии с российскими нормами СП 20.13330.2016: Нагрузки и воздействия
Подсказка
Это руководство основано на СП 20.13330.2016 и СП 63.13330.2012
.Теоретическая основа
В своде правил СП 20.13330.2016 «Нагрузки и воздействия» основное сочетание приведено в формуле (6. 1):
1):
- где: Pd — постоянные действия
Pl — долговременные переменные действия Pt — кратковременные переменные действия
Здесь описаны две две формулы:
для расчета группы 1 (предельная нагрузка) с использованием коэффициентов безопасности γf
Cm = γf ∙ Pd + (γf ∙ ψl1 ∙ Pl1 + γf ∙ ψl2 ∙ Pl2 + γf ∙ ψl3 ∙ Pl3 + …) + (γf ∙ ψt1 ∙ Pt1 + γf ∙ ψt2 ∙ Pt2 + γf ∙ ψt2 ∙ Pt2 + γf ∙ ψt2 ∙ Pt2 + γf ∙
для исполнения группы 2 (исправность) без коэффициентов запаса γf
Cm = Pd + (ψl1 ∙ Pl1 + ψl2 ∙ Pl2 + ψl3 ∙ Pl3 + …) + (ψt1 ∙ Pt1 + ψt2 ∙ Pt2 + ψt3 ∙ Pt3 + …)
для специальных комбинаций следует использовать первое уравнение с окончательным наложением, включающим специальную нагрузку Ps (например, случайные комбинации со случайным действием)
Cs = См + Ps
Независимо от использования коэффициентов безопасности уравнение 6. 1 состоит из двух частей переменного действия:
1 состоит из двух частей переменного действия:
первая часть для длительного переменного действия
(ψl1 ∙ Pl1 + ψl2 ∙ Pl2 + ψl3 ∙ Pl3 + …) при ψl1 = 1,0 и ψl2 = ψl3 = 0,95
Это означает: Pl1 – ведущее долгосрочное действие, а Pl2 и Pl3 – сопутствующие долгосрочные действия.
вторая часть для кратковременного переменного действия
(ψt1 ∙ Pt1 + ψt2 ∙ Pt2 + ψt3 ∙ Pt3 + …)
для исполнения группы 1 (предельная нагрузка) при ψt1 = 1,0, ψt2 = 0,9 и ψt3 = ψl4 = 0,7
для специальных комбинаций при ψt1 = 0,5 , ψt2 = ψt3 … = 0,3
Это означает: Pt1 — первое ведущее краткосрочное действие, Pt2 — второе ведущее краткосрочное действие и Pt3 и Pt4 — сопровождающие краткосрочные действия
Примечание
При действиях задаются коэффициенты ψt для расчета группы 1 (предельная нагрузка). Модифицированные коэффициенты для особых комбинаций необходимо учитывать при определении комбинации в MAXIMA.
Цели
Создание системы, включая код конструкции, материалы, сечения
Генерация действий с помощью задачи Action Manager или программы SOFiLOAD
Создание нагрузок внутри SOFiPLUS или с помощью программы SOFiLOAD
Запустить линейный анализ
Создание комбинаций действий
Создание суперпозиций
Описание проекта
В данном файле создается 2D система пластин. Пример сделан только для демонстрации действий по умолчанию с программой SOFiLOAD. и определения комбинаций с программой MAXIMA. Выбранный проектный код – СП 63-13330 «Бетонные и железобетонные конструкции» (2012).
Геометрия
Представлена простая двумерная пластина, разделенная на три части (три группы плоских элементов). Направление гравитации — это направление Z.
Материалы
Номер | Марка | Примечания |
|---|---|---|
1 | Б 35 (СП 63. | бетон f c = 19,5 МПа |
2 | А 500 (СП 63.13330) | арматурная сталь f y = 435 МПа, f t = 600 МПа |
Воздействия и загружения
Действие и его категория | Название | Варианты нагрузки |
|---|---|---|
G_C | Постоянный бетон, категория С, постоянный | 1 |
Г_С | Статическая нагрузка на грунт, категория S, постоянная | |
К | равномерно распределенные нагрузки, переменные кратковременные | 11,12 условный |
С | снеговая нагрузка переменная кратковременная | 21,22,23 условный |
Вт | ветровая нагрузка переменная кратковременная | 31,32,33 эксклюзивный |
ЛИ | стационарные установки, переменные долгосрочные | 41,42 |
ЛК | погрузчики и электромобили переменные долгосрочные | 51,52 условный |
ЛМ | хранящиеся материалы и продукты, переменные долгосрочные | 61,62,63 |
Действия и нагрузки определяются программой SOFiLOAD. Здесь используются только действия по умолчанию. Поэтому только имена действий
должны быть введены. Соответствующие коэффициенты безопасности и комбинированные коэффициенты добавляются автоматически.
Здесь используются только действия по умолчанию. Поэтому только имена действий
должны быть введены. Соответствующие коэффициенты безопасности и комбинированные коэффициенты добавляются автоматически.
- Комбинационные коэффициенты определяются здесь следующим образом:
коэффициенты ψl1 и ψt1 определяются при ψ0
коэффициенты ψl2 (= ψl3) и ψt2 определены при ψ1
коэффициент ψt3 определяется при ψ2
Распечатка таблицы Действия, включая соответствующие загружения, выглядит следующим образом:
Комбинации действий с использованием программы MAXIMA
Для комбинационного уравнения (6.1) согласно СП 20.13330.2016 необходимо сделать три предсуперпозиции и окончательно конверт о своих результатах. Процедура необходима, так как в каждом случае для кратковременных нагрузок и длительных нагрузок ведущая и должны быть определены сопутствующие действия.
В демонстрационных целях значением суперпозиции здесь является узловое значение PZ (опорная реакция). Узел 12 выбран для распечатки.
Узел 12 выбран для распечатки.
1-я предварительная накладка для постоянных действий
Создается явно определенная комбинация с использованием коэффициентов безопасности для постоянных действий. Тип результатов — none, потому что результирующие загружения не должны учитываться для более поздних расчетов. Сгенерированные номера загружений: 2155 и 2156.
Вход MAXIMA:
+ПРОГ МАКСИМА
Постоянные действия HEAD перед суперпозицией
эхо-нагрузка, факт
гребенка 1 доп. тип экспл. нет база 2100
! ДОБАВЬТЕ {G} все постоянные действия
!или
ДОБАВЬТЕ G_C facu gamu facf gamf ! действие G_C
ДОБАВИТЬ G_S facu gamu facf gamf ! действие G_S
supp 1 экстра мами etyp тип узла pz от 12 ! от 12 только для полной распечатки с эхом
КОНЕЦ
2-я предварительная суперпозиция для долгосрочных действий
Создается явно определенная комбинация с использованием коэффициентов безопасности и коэффициентов комбинации для долгосрочных воздействий. Тип результатов — «Нет», потому что результирующие загружения не должны учитываться для более поздних расчетов. Сгенерированный
номера загружений: 2255 и 2256.
Тип результатов — «Нет», потому что результирующие загружения не должны учитываться для более поздних расчетов. Сгенерированный
номера загружений: 2255 и 2256.
При входной строке ADD {Q1} facu psiu facf 0 определено, что опережающее действие должно определяться с неблагоприятным фактором γf ∙ ψ0 = буквальный psiu. Определение записи ADA LI,LC,LM определяет, что следует использовать только долгосрочные действия. Сопутствующие длительные действия приобретают неблагоприятный фактор γf ∙ ψ1 = буквально ps1u.
+ПРОГ МАКСИМА
HEAD предварительная суперпозиция долгосрочных действий
эхо-нагрузка, факт
гребень 2 доп. тип expl нет база 2200
ДОБАВИТЬ {Q1} facu psiu facf 0 ! первое ведущее действие
АДА ЛИ, ЛК, ЛМ! использовать только долгосрочные действия LI,LC,LM
ДОБАВИТЬ {QI} facu ps1u facf 0 ! сопутствующие действия
АДА ЛИ, ЛК, ЛМ! использовать только долгосрочные действия LI,LC,LM
супп 2 доп мами тип узла тип пз от 12 ! от 12 только для полной распечатки с эхом
КОНЕЦ
3-я предварительная суперпозиция для краткосрочных действий
Создается явно определенная комбинация с использованием коэффициентов безопасности и коэффициентов комбинации для краткосрочных действий. Тип результатов — «Нет», потому что результирующие загружения не должны учитываться для более поздних расчетов. Сгенерированный
номера загружений: 2355 и 2356.
Тип результатов — «Нет», потому что результирующие загружения не должны учитываться для более поздних расчетов. Сгенерированный
номера загружений: 2355 и 2356.
При входной строке ADD {Q1} facu psiu facf 0 определено, что 1-е опережающее действие должно определяться с неблагоприятным фактором γf ∙ ψ0 = буквальный psiu. Определение записи ADA Q,S,W определяет, что следует использовать только краткосрочные действия. Определение 2-го лидирующего действия определяется входной строкой ADD {Q2} facu ps1u facf 0, где неблагоприятный фактор равен γf ∙ ψ1 = литерал ps1u. Сопутствующие кратковременные действия приобретают неблагоприятный фактор γf ∙ ψ2 = буквально ps2u.
Для исполнения группы 1 (предельная нагрузка DESI):
+ПРОГ МАКСИМА
HEAD предварительная суперпозиция краткосрочных действий
эхо-нагрузка, факт
гребень 3 доп. тип expl нет база 2300
ДОБАВИТЬ {Q1} facu psiu facf 0 ! первое ведущее действие
АДА Q,S,W ! используйте только кратковременные действия Q,S,W
ДОБАВИТЬ {Q2} facu ps1u facf 0 ! второе ведущее действие
АДА Q,S,W ! используйте только кратковременные действия Q,S,W
ДОБАВИТЬ {QI} facu ps2u facf 0 ! сопутствующие действия
АДА Q,S,W ! используйте только кратковременные действия Q,S,W
супп 3 доп мами тип узла тип пз от 12 ! от 12 только для полной распечатки с эхом
КОНЕЦ
Для исполнения группы 1 (аварийная нагрузка ACCI):
При этом модифицированные коэффициенты комбинации ψt1, ψt2, ψt3 учитываются в формулах для неблагоприятного фактора FACU.
+ПРОГ МАКСИМА
HEAD предварительная суперпозиция краткосрочных действий
эхо-нагрузка, факт
гребень 3 доп. тип expl нет база 2300
ADD {Q1} facu '=0.5*gamu' facu 0 ! первое ведущее действие
АДА Q,S,W ! используйте только кратковременные действия Q,S,W
ADD {Q2} facu '=0.3*gamu' facu 0 ! второе ведущее действие
АДА Q,S,W ! используйте только кратковременные действия Q,S,W
ADD {QI} facu '=0.3*gamu' facu 0 ! сопутствующие действия
АДА Q,S,W ! используйте только кратковременные действия Q,S,W
супп 3 доп мами тип узла тип пз от 12 ! от 12 только для полной распечатки с эхом
КОНЕЦ
окончательный конверт
Наконец, необходимо выполнить окончательную огибающую результирующих загружений из предварительных наложений. Для этого стандартная комбинация
определяется спецификацией результирующих загружений из предварительных наложений. Тип результирующих загружений 2455 и 2456 является желаемым.
для того, чтобы использовать их в более позднем дизайне.
Вход MAXIMA для расчета группы 1 (предельная нагрузка DESI) выглядит следующим образом:
+ПРОГ МАКСИМА ГОЛОВНОЙ конверт эхо-нагрузка, факт расческа 4 дополнительных стана дези база 2400! введите desi для более позднего дизайна LC 2155,2156 тип AG1 ! загружения от предварительных постоянных воздействий в группе постоянных нагрузок AG1 LC 2255,2256 тип A2! Варианты нагружения от долговременных воздействий перед наложением в альтернативной группе нагружения A2 LC 2355,2356 тип A3! Варианты нагружения от кратковременных воздействий перед наложением в альтернативной группе нагружения A3 супп 4 доп мами тип узла тип пз от 12 ! от 12 только для полной распечатки с эхом КОНЕЦ
Окончательный ввод MAXIMA для специальной комбинации группы 1 (аварийная нагрузка ACCI):
+ПРОГ МАКСИМА Огибающая HEAD + случайное действие эхо-нагрузка, факт гребень 4 дополнительных станка типа acci base 2400 ! введите desi для более позднего дизайна ЛК 71,72 тип А10! действие вариантов нагрузки A исключительно в альтернативной группе A10 LC 2155,2156 тип AG1 ! загружения от предварительных постоянных воздействий в группе постоянных нагрузок AG1 LC 2255,2256 тип A2! Варианты нагружения от долговременных воздействий перед наложением в альтернативной группе нагружения A2 LC 2355,2356 тип A3! Варианты нагружения от кратковременных воздействий перед наложением в альтернативной группе нагружения A3 супп 4 доп мами тип узла тип пз от 12 ! от 12 только для полной распечатки с эхом КОНЕЦ
Анализ эффективности теплоизоляции многослойной железобетонной плиты с использованием слоя бетона с низкой теплопроводностью в климатических условиях Вьетнама
Открытый доступ
| Проблема | Веб-конференция MATEC. Том 251, 2018 VI Международная научная конференция «Интеграция, партнерство и инновации в строительной науке и образовании» (IPICSE-2018) | |
|---|---|---|
| Номер статьи | 04026 | |
| Количество страниц) | 8 | |
| Раздел | Моделирование и механика строительных конструкций | |
| DOI | https://doi.org/10.1051/matecconf/201825104026 | |
| Опубликовано онлайн | 14 декабря 2018 г. | |
- QCVN 02-2009, «Вьетнамские строительные нормы и правила, природные физические и климатические данные для строительства» (Стандарт, Вьетнам, 2009 г.) [Google Scholar]
- Э.
 А. Король Трёхслойные ограждающие железобетонные конструкции из лёгких бетонов и особенности их расчёта (Асв, Мок, 2001)
[Google Scholar]
А. Король Трёхслойные ограждающие железобетонные конструкции из лёгких бетонов и особенности их расчёта (Асв, Мок, 2001)
[Google Scholar] - Э.А. Король, В. Д. Тхо, Н. Х. Хоанг, MATEC Web Conf, 196, 02022 (2018) [Перекрестная ссылка] [Google Scholar]
- Э. Король, В. Д. Тхо, Ю. Кустикова, Серия конференций ИОП, 365 (5), 052033 (2018) [Перекрестная ссылка] [Google Scholar]
- И.
 Буйнак, Э.А. Король, В.Е. Латушкин, Связь, 1, 101 (2012)
[Google Scholar]
Буйнак, Э.А. Король, В.Е. Латушкин, Связь, 1, 101 (2012)
[Google Scholar] - Э.А. Король, Ю.А. Харкин, Вестник МГСУ, 3, 156–163 (2010). [Google Scholar]
- Э.А. Король, Е.М. Пугач, А. Харкину, Вестник МГСУ, 3, 67 (2014) [Google Scholar]
- С. Моавени, Анализ конечных элементов: теория и применение с ANSYS (Лондон, 2015 г.
 )
[Google Scholar]
)
[Google Scholar] - TCVN 4605-1988, «Стандарт проектирования изоляционных компонентов для методов нагрева» (Стандарт, Вьетнам, 1988 г.) [Google Scholar]
- QCVN 09-2013, «Национальный технический регламент по энергоэффективному строительству», (Стандарт, Вьетнам, 2013 г.) [Google Scholar]
- СП 63-13330-2012, Бетонные и железобетонные конструкции (Стандарт, Рус, 2012) [Google Scholar]
- ГОСТ Р 51263-2012 Полистиролбетон.


 13330)
13330)