Зависимость давления в колесах велосипедов, мотоциклов, автомобилей от температуры
Подробно о давлении в шинах велосипеда описано в отдельной статье на нашем сайте: «Давление в велосипедных шинах».
Здесь же мы обсудим только один нюанс: влияние температуры на давление в накачанном колесе. Причем это влияние имеет одинаковую природу и последствия для любых шин – велосипедных, мопедных, мотоциклетных и автомобильных.
От чего зависит температура воздуха в покрышке?
Прежде всего от температуры воздуха окружающей среды, где находится велосипед, (мотоцикл, автомобиль) при стоянке. Т.е. если колеса накачаны до давления 2,5 атмосферы дома или в гараже, где температура 20 °С, а затем байк (мотоцикл, автомобиль) выезжает на улицу, где температура +30 °С, то давление в шине уже чуть-чуть поднимается.
Далее. Колеса начинают катиться по горячему асфальту и соответственно нагреваются от соприкосновения с самим асфальтом и от возникающей силы трения резины об асфальт. В результате давление опять поднимается. Конечно, на велосипеде нагревание от трения заметно очень и очень мало и волнует только больших профессионалов на гонках, но при большом перепаде температур – в сильную жару или в холод это уже становится заметно. Этот фактор (нагрев от трения резины об асфальт) для автомобилистов и мотоциклистов гораздо важнее – скорости там значительно больше, чем на велосипеде и, соответственно, сила трения то же.
В результате давление опять поднимается. Конечно, на велосипеде нагревание от трения заметно очень и очень мало и волнует только больших профессионалов на гонках, но при большом перепаде температур – в сильную жару или в холод это уже становится заметно. Этот фактор (нагрев от трения резины об асфальт) для автомобилистов и мотоциклистов гораздо важнее – скорости там значительно больше, чем на велосипеде и, соответственно, сила трения то же.
Нельзя сказать, что этот вопрос критически важен, но учитывать его нужно и особенно это заметно при значительных перепадах: более 15-20 градусов.
Например, если велосипед хранится зимой в теплой квартире или отапливаемом гараже при температуре +20 – +25 °С, а кататься Вы выезжаете зимой на -10 °С, то перепад составляет 30-35 градусов. Едет велосипед по снегу, снежной корке или льду, холодному замёрзшему асфальту, у которого температура то же не +20, и в итоге давление в колесе уменьшается примерно на 0,3 bar. А это уже значительно.
Как рассчитать давление в колесе в зависимости от температуры?
Мы не будем глубоко вдаваться в физику процесса.
Это все объясняет закон Шарля (второй закон Гей-Люссака), о котором можно почитать в учебниках физики или в википедии.
Приведем его основную идею и формулу для расчета.
Закон Шарля гласит, что «Давление газа фиксированной массы и фиксированного объёма прямо пропорционально абсолютной температуре газа.» В накачанном колесе как раз газ (воздух) фиксированной массы и объёма и чем выше температура – тем выше давление. Зимой на холоде в колесах оно уменьшается, а летом на солнце – увеличивается.
Сама формула рассчета давления в шинах в зависимости от температуры воздуха выглядит следующим образом:
Пример расчета: Если известно давление в колесе при 0°С, например, оно составляет 2,5 атмосферы (bar), то для расчета давления при температуре 25°С используем эту формулу и получаем:
«Давление при 0°С» * (273 + 25) / 273
или
2,5 * (273+25) / 273 = 2,73 ≈ 2,7 bar
Еще раз напомним, что: 273 – это температура в градусах по шкале Кельвина, а не в градусах по Цельсию.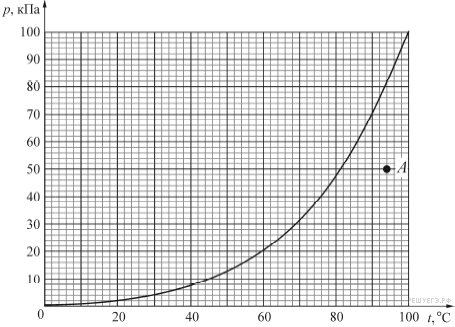
Для облегчения жизни приведем таблицу изменения давления в колесе, накаченном при 0°С, в зависимости от температуры воздуха.
Если Вы измеряли давление при +20°С и хотите понять какое оно станет зимой на улице при температуре -15°С, то формула примет вид:
2,5 * (273 + -15) / (273 + 20) = 2,5 * 258 / 293 = 2,2 bar
В общем случае, если считать очень грубо и приблизительно, то можно сказать, что при давлении более 2 bar изменение температуры на каждые 8-10 °С приводит к изменению давления примерно на 0,1 Bar.
Опять, же для удобства приведем таблицу быстрого получения значений давления в колесе в зависимости от температуры воздуха на улице, в случае, если байкер накачивал его дома, при +20 °С.
Изменение давления особенно нужно учитывать в случаях, если шины накачиваются летом в домашних условиях до давления близкого к максимальному и поездка предстоит по жаре или наоборот, колеса качаются близко до минимальных значений, а поездка предстоит по холоду.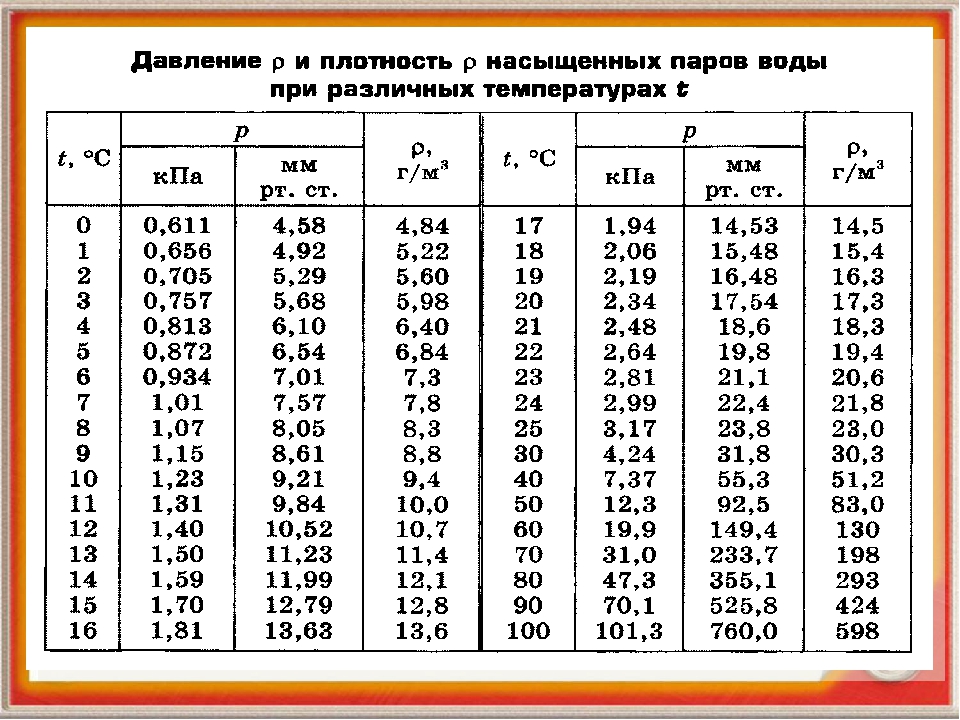 Главное, чтобы не выйти за пределы минимальных и максимальных значений, указанных на покрышке.
Главное, чтобы не выйти за пределы минимальных и максимальных значений, указанных на покрышке.
Эта таблица работает так же для мотоциклетных и автомобильных колес. Даже если их накачивают гелием. Гелий ведь то же газ и так же подчиняется всем законам физики, несмотря на то, что об этом говорят работники СТО.
Давление и Температура в Автоклаве: Какими Должны Быть?
Домашний автоклав помогает хозяйкам облегчить процесс консервации в разы и сэкономить время. Приготовление происходит при давлении, которое превышает атмосферное, и температуре более 100°С. Это необходимо в целях обеззараживания консервов от патогенных микроорганизмов, обезопасит продукты и увеличит срок годности.
В автоклаве во время стерилизации создается высокое давление, а поскольку агрегат плотно заперт, из него не может выйти ни жидкость, ни воздух.
Для избавления от всех вредных бактерий нужно прокипятить продукт при температуре от 100 градусов в течение минимум 20 минут.Некоторые виды патогенных организмов, в том числе ботулотоксин, способны выжить при таких условиях. Автоклав позволяет использовать более высокие температуры, при которых погибают любые бактерии.
Недостаток способа в том, что консервы могут сгореть в автоклаве, если передержать их. Всегда следуйте рецепту и придерживайтесь той температуры и давления, что убьет бактерии, но оставит продукцию в нормальном и съедобном виде. При каком давлении готовить в автоклаве зависит от вида продукции, необходимой температуры. Так, овощи не стоит готовить при показателе выше 100 градусов, а мясо нельзя обрабатывать ниже 110°С. Нормы температуры для приготовления разных продуктов можно прочитать в кулинарной книге, которая идет в комплекте с автоклавом.
Если повышать температуру в автоклаве, то вырастет и давление. Эти параметры взаимосвязаны.
Для правильного приготовления продуктов необходимо разобраться, какое давление должно
быть в автоклаве. Точное определение зависимости температуры от давления невозможно, так как есть другие факторы, которые влияют на показатели. Предлагаем ознакомительную таблицу зависимости температуры от абсолютного значения давления.
Точное определение зависимости температуры от давления невозможно, так как есть другие факторы, которые влияют на показатели. Предлагаем ознакомительную таблицу зависимости температуры от абсолютного значения давления.
| Р (атм) | Т (°С) |
|---|---|
| 1 | 6.7 |
| 1.3 | 45 |
| 2 | 80 |
| 3 | 100 |
| 3.5 | 110 |
| 4.5 | 120 |
| 5.5 | 126 |
| 6 | 132 |
| 8 | 142 |
Манометр в автоклаве показывает относительное значение давления. При температуре 110°С оно фиксирует 3.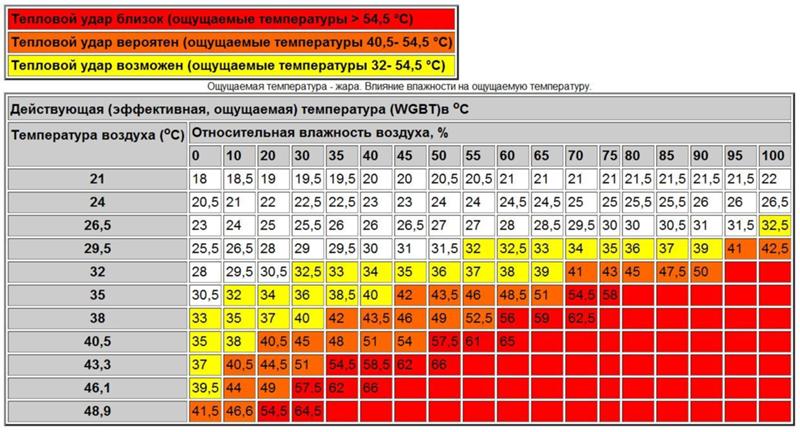 5 атм, если 120 градусов — от 4.5 атм. Давление зависит от скорости и температуры нагревания устройства, а также объема воздуха внутри, между крышкой и банками. В таблице значение двух Атм будет соответствовать показаниям манометра в 1 атм. Это может привести к путанице.
5 атм, если 120 градусов — от 4.5 атм. Давление зависит от скорости и температуры нагревания устройства, а также объема воздуха внутри, между крышкой и банками. В таблице значение двух Атм будет соответствовать показаниям манометра в 1 атм. Это может привести к путанице.
Воздух, которых находится внутри автоклава, сильно нагревается и расширяется быстрее. При 110°С внутри устройства будет больше 3 атм. Рекомендуем не ориентироваться на показания давления. Результативнее будет обращать внимание на термометр. Как только автоклав будет разогреваться до 110 градусов, стоит убавить нагрев.
Также важно учитывать время для готовки каждой консервы. Оно отличается, зависит от типа продукции.
- мясо — больше 30 минут;
- птица — 27 минут;
- рыба — 20 минут;
- грибы — 15 минут;
- овощи — 10 минут;
- фрукты — до 8 минут.
Стоит начинать отсчет времени приготовления с момента входа автоклава в рабочий режим.
Важно! От размера банок температура и давление не зависят, они остаются одинаковыми. Но при большом объеме время приготовления может увеличиваться на 5-15 минут.
Важно разобраться, какое давление и температура нужны для уничтожения микроорганизмов внутри консервов. Только автоклав может гарантировать безопасность продуктов при консервации.
Если вы не уверены в качестве мяса, лучше не консервировать его. Некоторые штаммы ботулизма способны выжить даже в экстремальных условиях.
Чтобы точно быть уверенным, какое давление накачивать в автоклав, стоит придерживаться таблицы и температуры нагрева. Для мясных и рыбных консервов оно должно быть более 105°С.
Современные модели автоклавов практически не требуют вмешательства человека. Необходимо только закачать давление и выставить нужную температуру. Когда устройство разогреется, сработает система, которая не позволит температуре расти.
Необходимо только закачать давление и выставить нужную температуру. Когда устройство разогреется, сработает система, которая не позволит температуре расти.
Консервы в среднем хранят от 2 до 5 лет. Если это рыба – больше двух лет хранить ее не рекомендують. Овощи могут не портится около трех лет, а мясные консервы – 5.
Читайте также:
- Режимы работи в автоклаве
- Что такое автоклав
- Гидравлические испытания автоклава
- Как пользоваться автоклавом
- Как выбрать автоклав
R-744 Таблица температуры и давления
Toolbox Home
°F | °С | ДАВЛЕНИЕ (psig) |
| °С | °F | ДАВЛЕНИЕ (бар) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| -40 | -40,0 | 131,0 | -40 | -40,0 | 9,05 | — 9006 13
| -38,9 | 137,0 | -39 | -38,2 | 9,42 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| -36 | -37,8 | 143,3 | -38 | -36,4 | 9,81 | 1 -3-36,7 | 149,7 | -37 | -34,6 | 10,20 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| -32 | -35,6 | 156,3 | -36 | -32,8 | 904-30 | -34,4 | 163,1 | -35 | -31,0 | 11,02 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| -28 | -33,3 | 170,1 | -34 | -29,2 | 90 10159 101 0005-26 | -32,2 | 177,3 | -33 | -27,4 | 11,89 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| -24 | -31,1 | 184,8 | -36 | 102 -25,1 34||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| -22 | -30,0 | 192,4 | -31 | -23,8 | 12,80 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| -20 | -28,9 | 200,2 | -30 6 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| -18 | -27,8 | 208,3 | -29 | -20,2 | 13,76 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| -16 | -26,7 | 216,5 |
| 14,26 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| -14 | -25,6 | 225,0 | -27 | -16,6 | 14,77 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| -12 | -24,4 | 233,8 | 54 | 6 -16 | 15,29 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| -10 | -23,3 | 242,7 | -25 | -13,0 | 15,83 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| -8 | -22,2 | 251,9 -12 9006 4 | -11,2 | 16,38 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| -6 | -21,1 | 261,3 | -23 | -9,4 | 16,94 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| -4 | -20,0 | 271,0 -2 9006 16,94 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| -7,6 | 17,51 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| -2 | -18,9 | 280,9 | -21 | -5,8 | 18,10 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 0 | -17,8 |
| -4,0 | 18,70 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2 | -16,7 | 301,5 | -19 | -2,2 | 19,31 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 4 | -15,6 | 312,1 9006 80 -1 | -0,4 | 19,94 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 6 | -14,4 | 323,1 | -17 | 1,4 | 20,58 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 8 | -13,3 | 33,3 33,002 4-16 | 3,2 | 21,24 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 10 | -12,2 | 345,7 | -15 | 5,0 | 21,91 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 12 | -11,1 | 357,4 | 1 9006 — 19054 900 6,822,59 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 14 | -10,0 | 369,5 | -13 | 8,6 | 23,29 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 16 | — | 381008 4-12 | 10,4 | 24,01 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 18 | -7,8 | 394,3 | -11 | 12,2 | 24,74 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 20 | -6,7 | 407,2 | 6 9006 — 1005414,0 | 25,49 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 22 | -5,6 | 420,4 | -9 | 15,8 | 26,25 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 24 | -4,4 | 43,008 4-8 | 17,6 | 27,03 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 26 | -3,3 | 447,6 | -7 | 19,4 | 27,82 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 28 | -2,2 | 461,7 | 6 — 11,2 | 28,63 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 30 | -1,1 | 476,1 | -5 | 23,0 | 29,46 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 32 | 0,0 | 4 4-4 | 24,8 | 30,30 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 34 | 1,1 | 505,8 | -3 | 26,6 | 31,16 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 36 | 2,2 | 521,2 | -2 1,1,4 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 38 | 3,3 | 536,9 | -1 | 30,2 | 32,94 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
ТЕМП °F 33 | ТЕМП °С | ДАВЛЕНИЕ (psig) |
| ТЕМП °С | ТЕМП °F | ДАВЛЕНИЕ (бар) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 40 | 4,4 | 552,9 | 0 | 32,0 | 30,8 5 | 42 | 5,6 | 569,3 | 1 | 33,8 | 34,78 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 6,7 | 586,0 | 2 | 35,6 | 35,73 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 46 | 1 306 90 910 7,83 | 37,4 | 36,70 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 48 | 8,9 | 620,5 | 4 | 39,2 | 30,6 5 | 50 | 10,0 | 638,3 | 5 | 41,0 | 38,70 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 11,1 | 656,5 | 6 | 42,8 | 39,72 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 54 6 | 501209 02,72 .7 | 44,6 | 40,77 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 56 | 13,3 | 694,0 | 8 | 46,4 | 901441,4 05 | 58 | 14,4 | 713,3 | 9 | 48,2 | 42,92 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1 | 15,6 | 733,1 | 10 | 50,0 | 44,02 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 62 | 11 | 51,8 | 45,15 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 64 | 17,8 | 773,8 | 12 | 53,6 | 904 1306 06 005 | 66 | 18,9 | 794,8 | 13 | 55,4 | 47,47 | 180006 180006 180006 180006 | 20,0 | 816,2 | 14 | 57,2 | 48,66 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 70 | 15 | 59,0 | 49,87 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 72 | 22,2 | 860,5 | 16 | 10,9 5 100011 60,9 100011 | 046|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 74 | 23,3 | 883,3 | 17 | 62,6 | 52,37 | 724,4 | 906,7 | 18 | 64,4 | 53,65 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 90 11 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 19 | 66,2 | 54,96 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 80 | 26,7 | 954,9 | 20 | 1929 50011 900 046 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 82 | 27,8 | 979,8 | 21 | 69,8 | 57,65 | 828,9 | 1005,4 | 22 | 71,6 | 59,03 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 90 1,0006 93 90 | 1 93 0006 1031,6 | 23 | 73,4 | 60. 44 44 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 88 | 31.1 | ** | 24 | 75.2 6041186 6041186 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 90 | 32,2 | ** | 25 | 77,0 | 63,34 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 92 | 33,3 | ** | 26 | 78,8 | 64,84 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 194 9006 11 | ** | 27 | 80,6 | 66,36 | |||||||||
| 96 | 35,6 | ** | 28 | 82,4 | 90 506 9 0 5 0 0 0 9 0 5 0 0 0 9 6 0 1 1 1 2 | 98 | 36,7 | ** | 29 | 84,2 | 69,51 | ||
| 100 | 37,8 | ** | 30 | 86,0 | 71,14 | ||||||||
| 102 | 1 90 8 | 9 0006 ** | 31 | 87,8 | 71,80 | ||||||||
| 104 | 40,0 | ** | 32 | 89,6 | **** | 60046 10 100006 41. 1 1 | ** | 33 | 91.4 | **** | |||
| 108 | 42,2 | ** | 34 | 93,2 | **** | 143,3 | ** | 35 | 95,0 | **** | |||
| 112 | 44,4 | ** | 36 | 96,8 | **** | ||||||||
| ** | 37 | 98.6 | **** | ||||||||||
| 116 | 46,7 | ** | 38 | 100,4 | **** | ||||||||
| ** | 39 | 102,2 | **** | ||||||||||
| 120 | 48,9 | ** | 40 | 104,0 | **** | ||||||||
ТЕМП °С | ДАВЛЕНИЕ (psig) |
| ТЕМП °С | ТЕМП °F | ДАВЛЕНИЕ (бар) | ||||||||
| 122 | 50,0 | ** | 41 | **** 11 | |||||||||
| 124 | 51. 1 1 | ** | 42 | 107,6 | **** | ||||||||
| 126 | 52,2 | ** | 43 | 90 101,1 900 **** 0046 | |||||||||
| 128 | 53,3 | ** | 44 | 111.2 | **** | ||||||||
| 130 | 54.4 | ** | 45 | 90 ****010103. 011 | |||||||||
| 132 | 55,6 | ** | 46 | 114,8 | **** | ||||||||
| 134 | 56,7 | ** | 47 6 6 90,001 906 106 0011 | ||||||||||
| 136 | 57,8 | ** | 48 | 118,4 | **** | ||||||||
| 138 | 58,9 | ** | 49 | 91 120,26 **** 046 | |||||||||
| 140 | 60,0 | ** | 50 | 122.0 | **** | ||||||||
| 142 | 61.1 | ** | 51 | 90 ****1 1 9000 0046 | |||||||||
| 144 | 62,2 | ** | 52 | 125,6 | **** | ||||||||
| 146 | 63,3 | ** | 53 | 127,4 | 9 **** 9004 9004 006 14864,4 | ** | 54 | 129,2 | **** | ||||
| 150 | 65,6 | ** | 55 | 131,0 | 6 **** 90 90 005456 | 132,8 | **** | ||||||
| 57 | 134,6 | **** | |||||||||||
| 596 381 | **** | ||||||||||||
| 59 | 138,2 | ** ** | |||||||||||
| 60 | 140. 0 0 | **** | |||||||||||
| 1 | 006 141,8 | **** | |||||||||||
| 62 | 143,6 | **** | |||||||||||
| 63 | 145,4 | **** 5 | 64 | 147,2 | **** | ||||||||
| 65 | 149,0 | **** |
** 87,8°F — критическая точка CO2, давление 1056,2 psig. Различных состояний жидкости и пара не существует.
**** 31,1°C – критическая точка CO2, давление 72,82 бар. Различных состояний жидкости и пара не существует.
Таблица свойств пара
- Главная
- Жидкости
- Пар
плотность, удельная теплоемкость, вязкость
| Температура [ O C] | Давление [бар] | c p [кДж/кгK] | ρ [кг/м3] | мк*10 6 [Па*с] | ν*10 6 [м2/с] |
|---|---|---|---|---|---|
| 0,0 | 0,0061 | 1,864 | 0,0048 | 8. 04 04 | 1675,0 |
| 10,0 | 0,0123 | 1,868 | 0,0094 | 8,45 | 898,94 |
| 20,0 | 0,0234 | 1,87 | 0,0173 | 8,85 | 511,56 |
| 30,0 | 0,0424 | 1,883 | 0,0304 | 9. 26 26 | 304,6 |
| 40,0 | 0,0737 | 1,894 | 0,0509 | 9,66 | 189,78 |
| 50,0 | 0,1233 | 1.907 | 0,0831 | 10,0 | 120,34 |
| 60,0 | 0,1992 | 1,924 | 0,1302 | 10,5 | 80,64 |
| 70,0 | 0,3117 | 1,944 | 0,1982 | 10,9 | 54,99 |
| 80,0 | 0,4736 | 1,969 | 0,2934 | 11. 3 3 | 38,51 |
| 90,0 | 0,7011 | 1,999 | 0,4235 | 11,7 | 27,63 |
| 100,0 | 1,013 | 2,135 | 0,598 | 11,97 | 20.02 |
| 110,0 | 1,43 | 2,177 | 0,826 | 12. 46 46 | 15.07 |
| 120,0 | 1,98 | 2.206 | 1,121 | 12,85 | 11.46 |
| 130,0 | 2,7 | 2,257 | 1,496 | 13.24 | 8,85 |
| 140,0 | 3,61 | 2,315 | 1,966 | 13. 54 54 | 6,89 |
| 150,0 | 4,76 | 2.395 | 2,547 | 13,93 | 5,47 |
| 160,0 | 6.18 | 2.479 | 3.258 | 14.32 | 4,39 |
| 170,0 | 7,92 | 2,583 | 4. 122 122 | 14,72 | 3,57 |
| 180,0 | 10.03 | 2.709 | 5.157 | 15.11 | 2,93 |
| 190,0 | 12.55 | 2,856 | 6.397 | 15,6 | 2,44 |
| 200,0 | 15. 55 55 | 3.023 | 7,862 | 15,99 | 2.03 |
| 210,0 | 190,08 | 3.199 | 9,588 | 16.38 | 1,71 |
| 220,0 | 23,2 | 3.408 | 11,62 | 16,87 | 1,45 |
| 230,0 | 27,98 | 3,634 | 13,99 | 17.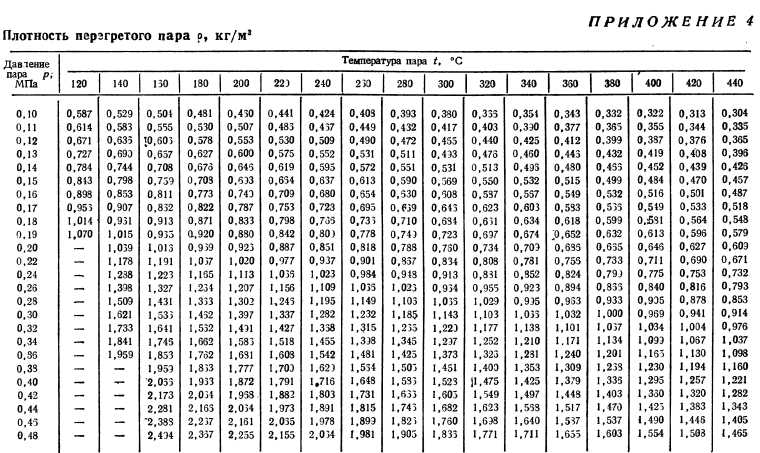 36 36 | 1,24 |
| 240,0 | 33,48 | 3.881 | 16,76 | 17,75 | 1,06 |
| 250,0 | 39,78 | 4.157 | 19,98 | 18.24 | 0,913 |
| 260,0 | 46,94 | 4. 467 467 | 23,72 | 18,83 | 0,794 |
| 270,0 | 55.05 | 4.815 | 28.09 | 19.32 | 0,688 |
| 280,0 | 64,19 | 5.234 | 33.19 | 19,91 | 0,6 |
| 290,0 | 74,45 | 5. 694 694 | 39.15 | 20.59 | 0,526 |
| 300,0 | 85,92 | 6,28 | 46.21 | 21.28 | 0,461 |
| 310,0 | 98,7 | 7.118 | 54,58 | 21,97 | 0,403 |
| 320,0 | 112,9 | 8. 206 206 | 64,72 | 22,85 | 0,353 |
| 330,0 | 128,65 | 90,881 | 77,1 | 23,93 | 0,31 |
| 340,0 | 146.08 | 12.35 | 92,76 | 25,2 | 0,272 |
| 350,0 | 165,37 | 16. |

 28
28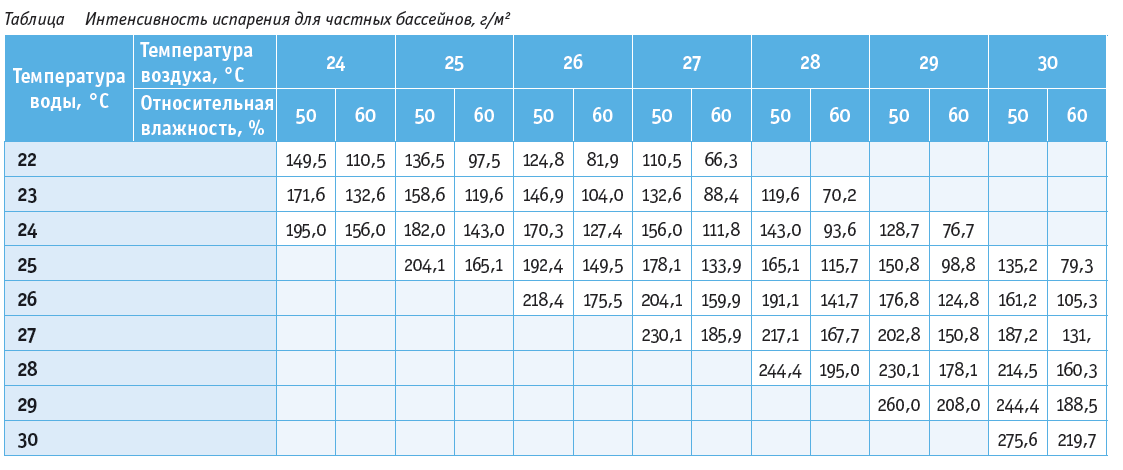 04
04 0
0