Задание В12, открытого банка ЕГЭ по математике
Похожие презентации:
Элементы комбинаторики ( 9-11 классы)
Применение производной в науке и в жизни
Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»
Знакомство детей с математическими знаками и монетами
Тренажёр по математике «Собираем урожай». Счет в пределах 10
Методы обработки экспериментальных данных
Лекция 6. Корреляционный и регрессионный анализ
Решение задач обязательной части ОГЭ по геометрии
Дифференциальные уравнения
Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи
Здравствуйте!
Сегодня мы продолжим рассмотрение практикоориентированных задач из открытого банка заданий ЕГЭ по
математике, и остановимся на задании В12 — физические задачи.
Как правило , в заданиях этого типа функциональная
зависимость в виде формулы включена в условие задачи, там же
даны значения всех параметров и констант, выраженных в
нужной системе единиц.
Приступая к выполнению задания В12, требуется :
1) проанализировать условие и вычленить формулу ,
описывающую заданную ситуацию, и все значения, которые
надо в эту формулу подставить
2) Составить уравнение или неравенство и решить его
3) Проанализировать полученный результат (выделить нужный
ответ)
Рассмотрим несколько заданий типа В12. Условие первой
задачи вы сейчас видите на своих экранах.
Задание №1
l (t ) l0 (1 t )
0
0
l (t 0 ) l0 l0 t 0
l0 2 10 4 20000 мм;
1,2 10 5 ( 0C ) 1.
t 0 ? при l (t 0 ) 20009 мм
l (t 0 ) 20000 2 104 1,2 10 5 t 0
l (t 0 ) 0,24 t 0 20000
20009 0,24 t 0 20000
9 0,24 t 0
9
t
37,50 С
0,24
0
Ответ: 37,5
Задание №2
В боковой стенке высокого цилиндрического бака у самого дна
закреплён кран.
После его открытия вода начинает вытекать из бака,при этом высота столба воды в нём, выраженная в метрах, меняется по
g 2 2 , где t — время в секундах,
закону H (t ) H
2gH kt k t
=
0
—
0
2
1
прошедшее с момента открытия крана, k = 200 — отношение
площадей поперечных сечений крана и бака, Н0 = 5 м — начальная
высота столба воды, а g — ускорение свободного падения (считайте g =
10 м/с2). Через сколько секунд после открытия крана в баке останется
четверть первоначального объёма воды?
g 22
Н (t ) H 0 2 gH 0 kt k t
2
5
1
1 2
5 t
t
4
20 8000
1
g 10 м / с , k
, H0 5 м
200
t 2 400t 30000 0.
2
t ?
1
5
4
4
t1 300, t2 100 t наим.
Ответ: 100.
Задание №3
Зависимость температуры (в градусах Кельвина) от времени для
нагревательного элемента некоторого прибора была получена
экспериментально и на исследуемом интервале температур
определяется выражением T(t) = T0 + bt + at2 , где t — время в
минутах, T0 = 1450 К, a = — 12,5 К/мин2 , b = 175 К/мин.
Известно,что при температуре нагревателя свыше 1750 К прибор может
испортиться, поэтому его нужно отключать. Определите, через
какое наибольшее время после начала работы нужно отключать
прибор. Ответ выразите в минутах.
T (t ) T0 bt at 2
T0 1450, a 12,5, b 175
t наиб . 0 при T (t ) 1750
1450 175t 12,5t 2 1750
t 2 14t 24 0
2
12
t
Ответ: 2
(меньший корень)
Задание №4
Груз массой 0,08 кг колеблется на пружине со скоростью, меняющейся по
закону
English Русский Правила
Отверстие и свободный поток – Лабораторное руководство по прикладной гидромеханике
Отверстие – это отверстие любого размера или формы в трубе или на дне или боковой стенке емкости (бака для воды, резервуара и т. д.), через которое выпускается жидкость. Если известны геометрические свойства отверстия и присущие жидкости свойства, отверстие можно использовать для измерения скорости потока. Измерение расхода с помощью отверстия основано на применении уравнения Бернулли, которое утверждает, что существует зависимость между давлением жидкости и ее скоростью.
Скорость потока и расход, рассчитанные на основе уравнения Бернулли, должны быть скорректированы с учетом влияния потерь энергии и вязкости. Поэтому для получения точных результатов коэффициент скорости ( C v ) и коэффициент расхода (
Дроссели имеют множество применений в инженерной практике, помимо измерения расхода жидкости в трубах и резервуарах. Поток, поступающий в водопропускную трубу или впускное отверстие ливневой канализации, может действовать как поток через отверстие; нижний выход плотины — еще один пример. Коэффициенты скорости и расхода необходимы для точного прогнозирования скорости потока из отверстий.
Целью этого лабораторного эксперимента является определение коэффициентов скорости и расхода двух небольших отверстий в лаборатории и сравнение их со значениями в учебниках и других надежных источниках.
Коэффициенты скорости и расхода определяются путем измерения траектории струи, выбрасывающей жидкость из отверстия в стенке резервуара в условиях стационарного потока, т. е. при постоянном напоре резервуара.
Для проведения эксперимента с отверстием и свободным потоком струи требуется следующее оборудование:
- Стенд гидравлики F1-10;
- Ф1-17 аппарат со соплами и безнапорными струями, с двумя соплами диаметром 3 и 6 мм;
- Мерный цилиндр для измерения расхода; и
- Секундомер для измерения времени измерения расхода.
Устройство с диафрагмой и безнапорным потоком состоит из цилиндрического напорного бака с установленной сбоку диафрагмой (рис. 6.1). Регулируемая переливная труба находится рядом с напорным баком, что позволяет изменять уровень воды. Гибкий шланг, прикрепленный к переливной трубе, возвращает лишнюю воду на гидравлический стенд. Шкала, прикрепленная к головному баку, показывает уровень воды. Перегородка в основании напорного бака обеспечивает равномерный поток внутри бака за диафрагмой.
Рисунок 6.1: Сопло Armfield F1-17 и струйный аппарат
Скорость истечения через отверстие можно рассчитать, применив уравнение Бернулли (для стационарного несжимаемого потока без трения) к большому резервуару с отверстием (отверстием) сбоку (рис. 6.2):
, где h — высота жидкости над отверстием. Это идеальная скорость, поскольку влияние вязкости жидкости не учитывается при выводе уравнения 1. Однако фактическая скорость потока меньше v i и рассчитывается как:
C v коэффициент скорости , учитывающий влияние вязкости; поэтому C v <1.
Фактическая скорость оттока, рассчитанная по уравнению (2), представляет собой скорость на сужении вены, , где диаметр струи наименьший, а скорость потока максимальна (рис. 6.2).
Фактическая скорость оттока может быть рассчитана как:
, где A c — площадь кровотока в области контрактной вены. A c меньше площади отверстия, A o (рис. 6.2), и определяется как:
где C c — коэффициент сжатия; следовательно, C c < 1,
Подстановка v и A c из уравнений 2 и 4 в уравнение 3 приводит к следующему результату:
Произведение C v C c называется коэффициентом расхода, C d ; Таким образом, уравнение 5 можно записать как:
Коэффициент скорости C v и коэффициент расхода C d определяются экспериментально следующим образом.
Если пренебречь влиянием сопротивления воздуха на струю, выходящую из отверстия, то можно считать, что горизонтальная составляющая скорости струи остается постоянной. Следовательно, горизонтальное расстояние, пройденное струей (x) за время (t), равно:
Вертикальная составляющая траектории струи будет иметь постоянное ускорение вниз из-за силы тяжести. Следовательно, в любой момент времени t положение струи по оси Y можно рассчитать как:
Уравнение преобразования (8) дает:
Замена t и v из уравнений 9 и 2 в уравнение 7 приводит к:
Уравнения (10) можно изменить, чтобы найти C v :
Таким образом, для стационарных условий потока (т. е. постоянного h в напорном баке) значение C v можно определить по координатам x, y траектории струи.
График x 9График зависимости 0006 будет иметь наклон 2 C против .
Если C d считать постоянным, то график зависимости Q от (уравнение 6) будет линейным, а наклон этого графика будет равен:
Этот эксперимент будет состоять из двух частей. Часть A выполняется для определения коэффициента скорости, а часть B проводится для определения коэффициента расхода.
Настройте оборудование следующим образом:
- Найдите аппарат над желобом в верхней части скамейки.
- С помощью спиртового уровня, прикрепленного к основанию, выровняйте аппарат, отрегулировав ножки.
- Подсоедините гибкую впускную трубку сбоку напорного резервуара к быстроразъемному фитингу.
- Поместите свободный конец гибкой трубки от регулируемого перелива сбоку напорного бака в объемный. Убедитесь, что эта трубка не будет мешать траектории струи, вытекающей из отверстия 9.0022
- Закрепите каждую иглу в поднятом положении, затянув винт с накатанной головкой.
- Установите 3-мм отверстие в фитинг с правой стороны напорного бака, используя два прилагаемых крепежных винта. Убедитесь, что уплотнительное кольцо установлено между отверстием и баком.
- Закройте клапан управления потоком стенда, включите насос, а затем постепенно откройте клапан управления потоком стенда. Когда уровень воды в напорном бачке достигнет верха переливной трубы, отрегулируйте клапан управления потоком скамьи так, чтобы уровень воды был на 2–3 мм выше уровня переливной трубы. Это обеспечит постоянный напор и постоянный поток через отверстие.
- При необходимости отрегулируйте рамку так, чтобы ряд игл был параллелен жиклеру, но располагался на 1 или 2 мм позади него. Это позволит избежать возмущения струи, но сведет к минимуму ошибки из-за параллакса.
- Прикрепите лист бумаги к спинке между иглами и доской и закрепите его с помощью прилагаемого зажима так, чтобы его верхний край был горизонтальным.
- Расположите переливную трубку так, чтобы обеспечить высокий напор (например, 320 мм). Траектория струи получается с помощью игл, установленных на вертикальном щите, чтобы следовать профилю струи.
- Ослабьте фиксирующий винт для каждой иглы и перемещайте иглу, пока ее острие не окажется непосредственно над форсункой. Снова затяните винт.
- Отметьте на бумаге положение верхней части каждой иглы. Отметьте горизонтальное расстояние от плоскости отверстия (принятое как ) до координатной точки, обозначающей положение первой иглы. Эта первая координатная точка должна быть достаточно близко к отверстию, чтобы рассматривать ее как имеющую значение y=0. Таким образом, смещения y измеряются относительно этого положения.
- Объемный расход через отверстие можно определить путем перехвата струи с помощью мерного цилиндра и секундомера. Измеренные скорости потока будут использоваться в Части B.
Таким образом, смещения y измеряются относительно этого положения.- Повторите этот тест для нижних крышек резервуаров (например, 280 мм и 240 мм)
Повторите описанную выше процедуру для второго отверстия диаметром 6 мм.
Часть B: Определение коэффициента расхода при постоянном напоре- Расположите переливную трубку так, чтобы ее высота в резервуаре составляла 300 мм. (Возможно, для этого вам придется отрегулировать уровень переливной трубки.)
- Измерьте скорость потока путем сбора по времени с помощью прилагаемого мерного цилиндра.
- Повторите эту процедуру для головки 260 мм.
Процедуру следует повторить и для второго отверстия.
Перейдите по этой ссылке, чтобы получить доступ к рабочей книге Excel для этого эксперимента.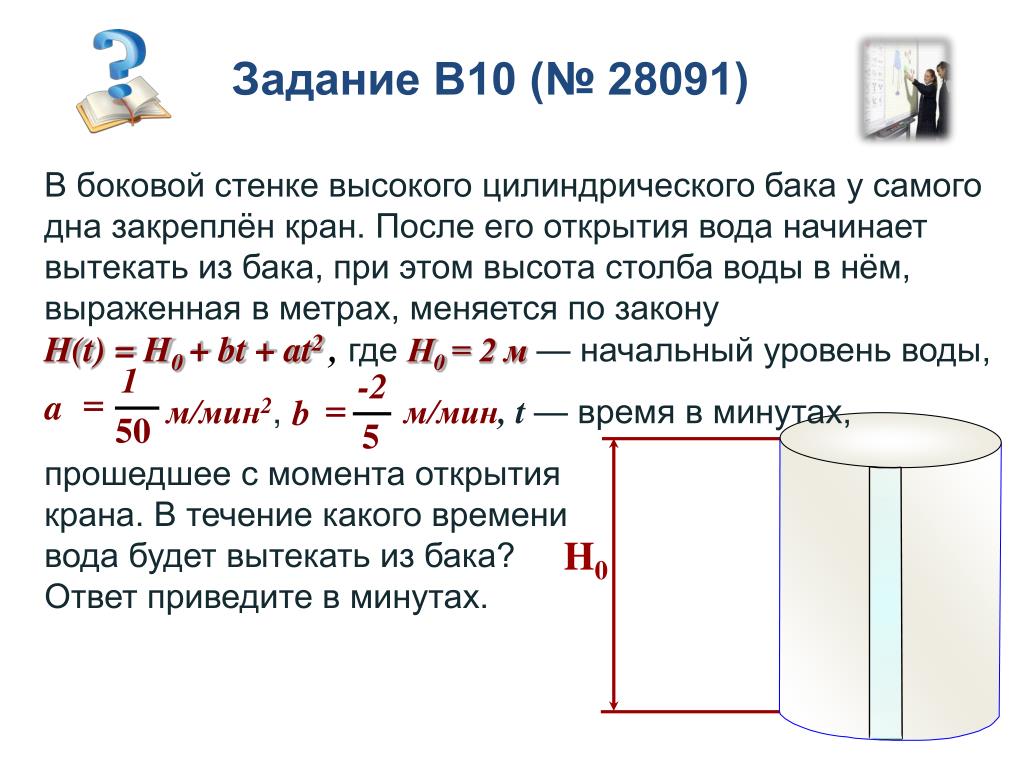
Используйте следующие таблицы для записи ваших измерений.
Таблица исходных данных: часть A| Игла № | Отверстие Диаметр (м) | x (м) | Напор (м) | г(м) | ||||
| Пробная версия 1 | Испытание 2 | Пробная версия 3 | Пробная версия 1 | Испытание 2 | Пробная версия 3 | |||
| 1 | 0,003 | 0,014 | ||||||
| 2 | 0,064 | |||||||
| 3 | 0,114 | |||||||
| 4 | 0,164 | |||||||
| 5 | 0,214 | |||||||
| 6 | 0,264 | |||||||
| 7 | 0,314 | |||||||
| 8 | 0,364 | |||||||
| Игла № | Отверстие Диаметр (м) | x (м) | Напор (м) | г(м) | ||||
| Пробная версия 1 | Испытание 2 | Пробная версия 3 | Пробная версия 1 | Испытание 2 | Пробная версия 3 | |||
| 1 | 0,006 | 0,014 | ||||||
| 2 | 0,064 | |||||||
| 3 | 0,114 | |||||||
| 4 | 0,164 | |||||||
| 5 | 0,214 | |||||||
| 6 | 0,264 | |||||||
| 7 | 0,314 | |||||||
| 8 | 0,364 | |||||||
Тест | Отверстие Диаметр (м) | Головка (м) | Объем (л) | Время (с) |
| 1 | 0,003 | |||
| 2 | ||||
| 3 | ||||
| 4 | ||||
| 5 | ||||
| 6 | 0,006 | |||
| 7 | ||||
| 8 | ||||
| 9 | ||||
| 10 |
2. Расчеты Рассчитайте значения (y.h) 1/2 для части A и сброса ( Q ) и ( h 0,5 ) для части B. Запишите свои расчеты в следующие таблицы результатов.
В соответствующих расчетах используются следующие размеры оборудования. При необходимости эти значения могут быть проверены в рамках экспериментальной процедуры и заменены вашими измерениями [6].
– Диаметр малого отверстия: 0,003 м
– Диаметр большого отверстия: 0,006 м
– Шаг спиц: 0,05 м
| Игла № | Отверстие Диаметр (м) | x (м) | Напор (м) | г(м) | (ж.  ч) 1/2 (м) | ||||||
| Пробная версия 1 | Испытание 2 | Пробная версия 3 | Пробная версия 1 | Испытание 2 | Пробная версия 3 | Пробная версия 1 | Испытание 2 | Пробная версия 3 | |||
| 1 | 0,003 | 0,014 | |||||||||
| 2 | 0,064 | ||||||||||
| 3 | 0,114 | ||||||||||
| 4 | 0,164 | ||||||||||
| 5 | 0,214 | ||||||||||
| 6 | 0,264 | ||||||||||
| 7 | 0,314 | ||||||||||
| 8 | 0,364 | ||||||||||
| Игла № | Отверстие Диаметр (м) | x (м) | Напор (м) | г(м) | (ж.  ч) 1/2 (м) | ||||||
| Пробная версия 1 | Испытание 2 | Испытание 3 | Пробная версия 1 | Испытание 2 | Пробная версия 3 | Пробная версия 1 | Испытание 2 | Пробная версия 3 | |||
| 1 | 0,006 | 0,014 | |||||||||
| 2 | 0,064 | ||||||||||
| 3 | 0,114 | ||||||||||
| 4 | 0,164 | ||||||||||
| 5 | 0,214 | ||||||||||
| 6 | 0,264 | ||||||||||
| 7 | 0,314 | ||||||||||
| 8 | 0,364 | ||||||||||
Тест | Отверстие Диаметр (м) | Головка (м) | Объем (л) | Время (с) | Объем (м 3 ) | Q (м 3 /сек) | ч 0,5 (м 0,5 ) |
| 1 | 0,003 | ||||||
| 2 | |||||||
| 3 | |||||||
| 4 | |||||||
| 5 | |||||||
| 6 | 0,006 | ||||||
| 7 | |||||||
| 8 | |||||||
| 9 | |||||||
| 10 |
Используйте предоставленный шаблон для подготовки лабораторного отчета для этого эксперимента.
Ваш отчет должен включать следующее:
- Таблица(и) исходных данных
- Таблицы результатов
- График(и)
Часть A : На одной диаграмме постройте график значений x (ось Y) и (yh) 1/2 значений (ось X) для каждого теста. Рассчитайте наклон этих графиков, используя уравнение наилучшего соответствия вашим экспериментальным данным и установив точку пересечения на ноль. Используя уравнение 11, рассчитайте коэффициент скорости для каждого отверстия как:
Часть B : График значений Q (ось Y) в зависимости от (h) 0,5 значений (ось X). Определите наклон этого графика, используя уравнение наилучшего соответствия вашим экспериментальным данным и установив точку пересечения равной нулю. На основе уравнения 12 рассчитайте коэффициент расхода для каждого отверстия, используя уравнение наилучшего соответствия для ваших экспериментальных данных и следующую зависимость:
- Найдите рекомендуемые значения для C 9(-2)). Скорость истечения
CENGAGE PHYSICS АНГЛИЙСКИЙ-МЕХАНИКА ЖИДКОСТИ-Связанное понимание
20 видеоРЕКЛАМА
Ab Padhai karo bina ads ke
Khareedo DN Pro and dekho sari videos bina kisi ad ki rukaavat ke!
Ответить
Пошаговое решение от экспертов, которое поможет вам в решении вопросов и получении отличных оценок на экзаменах.
Похожие видео
Имеются два одинаковых небольших отверстия площадью поперечного сечения a на противоположных сторонах резервуара с жидкостью плотностью ρ. Разница по высоте между отверстиями составляет h. Резервуар стоит на гладкой горизонтальной поверхности. Горизонтальная сила, которую необходимо приложить к баку, чтобы удержать его в неравновесном состоянии, равна 9(2) производится в правой вертикальной стене на высоте y=20см от расчетного дна. (я). скорость оттока (ii). горизонтальная сила F, удерживающая цилиндр в статическом равновесии, если он находится на гладкой горизонтальной плоскости (iii).
минимальное и максимальное значение F, чтобы удерживать цилиндр в состоянии покоя. Коэффициент трения между цилиндром и плоскостью mu=0,1 (iv). скорость самого верхнего слоя столба жидкости, а также скорость границы, разделяющей две жидкости.14159419 9(-2) ) Минимальное и максимальное значения F для удержания цилиндра в статике сразу после того, как вода начнет проливаться через отверстие. Если коэффициент статического трения между контактными поверхностями равен 0,01
327883206
Имеются два одинаковых маленьких отверстия, каждое площадью поперечного сечения a на противоположных сторонах резервуара, содержащего жидкость с плотностью rho . Разница в высоте между штамбами h. Танк стоит на гладкой горизонтальной поверхности. Найдите горизонтальную силу, которую необходимо приложить к баку, чтобы он оставался в равновесии.
642716219
Текст Решение
Имеются два одинаковых небольших отверстия, каждое площадью поперечного сечения на противоположных сторонах резервуара, содержащего жидкость с плотностью rho .
Разница в высоте между отверстиями равна «h». Танк лежит на гладкой горизонтальной поверхности. Найдите горизонтальную силу, которую необходимо приложить к баку, чтобы удержать его в равновесии.642729562
Текст Решение
На противоположных сторонах емкости с жидкостью плотностью ρ имеются два одинаковых маленьких отверстия, каждое площадью поперечного сечения. Разница в высоте между отверстиями равна «h». Танк лежит на гладкой горизонтальной поверхности. Найдите горизонтальную силу, которую необходимо приложить к баку, чтобы удержать его в равновесии. 9(2) Есть отверстие в области. Тогда расход воды равен
642954483
На противоположных сторонах емкости с жидкостью плотностью rho расположены два одинаковых небольших отверстия площадью поперечного сечения a. Разница по высоте между отверстиями составляет h . Резервуар стоит на гладкой горизонтальной поверхности. Горизонтальная сила, которую необходимо приложить к резервуару, чтобы удерживать его в неравновесном состоянии, равна
644103125
Цилиндрический сосуд очень большой площади поперечного сечения содержит две несмешивающиеся жидкости с плотностью ρ1=600 кг/м3 и ρ2=1200 кг/м3.
Скорость истечения
минимальное и максимальное значение F, чтобы удерживать цилиндр в состоянии покоя. Коэффициент трения между цилиндром и плоскостью mu=0,1 (iv). скорость самого верхнего слоя столба жидкости, а также скорость границы, разделяющей две жидкости.
Разница в высоте между отверстиями равна «h». Танк лежит на гладкой горизонтальной поверхности. Найдите горизонтальную силу, которую необходимо приложить к баку, чтобы удержать его в равновесии.