6.22.2. Изменение частоты вращения двигателя изменением частоты сети
Этот метод изменения скорости вращения возможен только в том случае, когда имеется специальный преобразователь, позволяющий получать трехфазное напряжение регулируемой частоты. Эту роль может выполнить синхронный генератор с изменяющейся скоростью вращения. В настоящее время широко используются статические полупроводниковые преобразователи частоты.
При питании асинхронного двигателя от источника переменного тока регулируемой частоты необходимо учитывать то, что электромеханические параметры двигателя будут различными на разных частотах (рис. 6.53).
Рис. 6.53
Величина критического скольжения механической характеристики
при уменьшении частоты увеличивается. Максимальный момент в соответствии с формулой
также
увеличивается с уменьшением частоты.
Аналогично изменяется и величина
пускового момента. Изменение вида
механической характеристики при
изменении частоты питающего напряжения
должно учитываться в системах частотного
управления асинхронным двигателем. С
изменением частоты изменяются и рабочие
характеристики двигателей, так как при
уменьшении частоты увеличивается ток
холостого хода двигателя, сопровождающийся
увеличением магнитного потока при
неизменном напряжении питания. Все
изменения приводят к необходимости
одновременного изменения частоты сети
и питающего напряжения.
Взаимозависимость напряжения и частоты сети определяются реальными условиями работы двигателя. При постоянном моменте нагрузки желательно сохранить неизменным значение максимального момента, развиваемого двигателем, т. е. не зависящим от частоты питающей сети. Но как следует из ранее приведенной формулы
или ; .
Откуда
следует, что для поддержания максимального
момента механической характеристики
необходимо напряжение сети изменять
пропорционально ее частоте.
Если по условиям эксплуатации при изменении частоты вращения должна оставаться неизменной мощность на валу двигателя, т. е.
или ,
то напряжение и частота сети должны быть связаны между собой соотношением
,
где напряжение сети при частоте ;
напряжение сети при частоте .
6.22.3. Регулирование частоты вращения ротора асинхронных двигателей изменением сопротивления роторной цепи
Рис. 6.54
Как уже было сказано ранее, общий вид механической характеристики и, прежде всего, критическое скольжение при прочих равных условиях зависят от сопротивления роторной обмотки.
Этот способ регулирования скорости заключается в введении сопротивления в цепь ротора (рис. 6.54). Ранее мы уже видели, что увеличение сопротивления роторной цепи увеличивает критическое скольжение. Если момент сопротивления на оси двигателя неизменный и если увеличить сопротивление роторной цепи, скольжение увеличится и скорость вращения пропорционально уменьшится.
Рис. 6.55
На рис. 6.55 представлено семейство механических характеристик двигателя при различных сопротивлениях реостата, включенного последовательно с роторной обмоткой. Если сопротивление реостата в цепи ротора равняется нулю, то при моменте нагрузки скольжение в соответствии с механической характеристикой 0 равно . Если сопротивление реостата не равно нулю (характеристика 1), угол наклона прямолинейной части механической характеристики уменьшится и двигатель обеспечит устойчивую работу при скольжении , т.
е. при меньшей частоте вращения ротора.
При дальнейшем увеличении сопротивления
дополнительного трехфазного реостата
частота вращения будет уменьшаться.
При больших сопротивлениях реостата
работа двигателя становится менее
устойчивой, так как даже малое изменение
момента на валу двигателя приводит к
значительному изменению частоты
вращения.Таким способом можно изменить частоту ротора в пределах от номинального скольжения и до полной остановки двигателя. Этот способ регулирования скорости неэффективен, так как связан с большими потерями электрической энергии. Механическая мощность уменьшается пропорционально уменьшению частоты вращения ротора при постоянном механическом моменте, и в то же время потери в дополнительном сопротивлении ротора увеличиваются пропорционально.
Скорость
вращения может быть изменена изменением
напряжения питания, но этот метод
регулирования используют очень редко,
так как область устойчивого регулирования
очень ограничена.
Скалярное управление
Дмитрий Левкин
Отношение В/Гц вычисляется на основе номинальных значений (напряжения и частоты) контролируемого электродвигателя переменного тока. Поддерживая постоянным значение отношения В/Гц мы можем поддерживать относительно постоянным магнитный поток в зазоре двигателя. Если отношение В/Гц увеличивается тогда электродвигатель становится перевозбужденным и наоборот если отношение уменьшается двигатель находится в недовозбужденном состоянии.
Зависимость частоты питания двигателя от времени при скалярном упрравлении
Изменение напряжения питания электродвигателя при скалярном управлении
На низких оборотах необходимо компенсировать падение напряжения на сопротивлении статора, поэтому отношение В/Гц на низких оборотах устанавливают выше чем номинальное значение. Скалярный метод управления наиболее широко используется для управления асинхронными электродвигателями.
В применении к асинхронным двигателям
При скалярном методе управления, скорость асинхронного электродвигателя контролируется установкой величины напряжения и частоты статора, таким образом, чтобы магнитное поле в зазоре поддерживалось на нужной величине.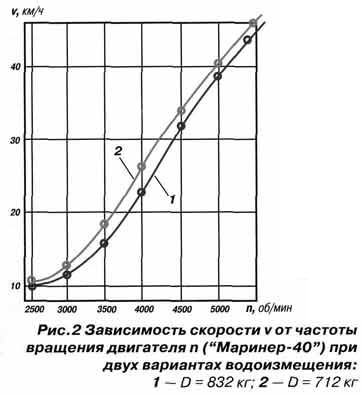
Для поддержания постоянного магнитного поля в зазоре, отношение В/Гц должно быть постоянным на разных скоростях.
Скалярное управление без датчика скорости
При увеличении скорости напряжение питания статора так же должно пропорционально увеличиваться. Однако синхронная частота асинхронного двигателя не равна частоте вращения вала, а скольжение асинхронного двигателя зависит от нагрузки. Таким образом система контроля со скалярным управлением без обратной связи не может точно контролировать скорость при наличии нагрузки. Для решения этой задачи в систему может быть добавлена обратная связь по скорости, а следовательно и компенсация скольжения [2].
Скалярное управление с датчиком скорости
Скалярное управление электродвигателями переменного тока — хорошая альтернатива для приложений, где нет переменной нагрузки и не требуется хорошая динамика (вентиляторы, насосы). Для работы скалярного управления не требуется датчик положения ротора, а скорость ротора может быть оценена по частоте питающего напряжения.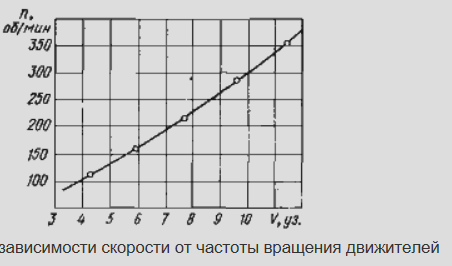
При скалярном управлении электродвигателем токи статора не контролируются напрямую.
СДПМ со скалярным методом управления может легко стать неуправляемым (выйти из синхронного состояния) особенно когда момент нагрузки превышает значение предельного момента электропривода. Скалярный метод не подходит для контроля СДПМ на низких оборотах для приложений, требующих высокую динамику [1].
- Метод скалярного управления относительно прост в реализации, но обладает несколькими существенными недостатками:
- во-первых, если не установлен датчик скорости нельзя управлять скоростью вращения вала асинхронного двигателя, так как она зависит от нагрузки (наличие датчика скорости решает эту проблему), а вслучае с синхронным двигателем при изменении нагрузки — можно совсем потерять управление;
- во-вторых, нельзя управлять моментом.
Конечно, эту задачу можно решить с помощью датчика момента, но стоимость его установки очень высока, и будет скорее всего выше самого электропривода. При этом управление моментом будет очень инерционным; - также нельзя управлять одновременно моментом и скоростью.
Конечно, эту задачу можно решить с помощью датчика момента, но стоимость его установки очень высока, и будет скорее всего выше самого электропривода. При этом управление моментом будет очень инерционным;Скалярное управление достаточно для большинства задач в которых применяется электропривод с диапазоном регулирования частоты вращения двигателя до 1:10.
Когда требуется максимальное быстродействие, возможность регулирования в широком диапазоне скоростей и возможность управления моментом электродвигателя используется векторное управление.
- Cristian Busca. Open loop low speed control for PMSM in high dynamic application.- Aalborg, Denmark.: Aalborg universitet, 2010
- Bial Akin, Nishant Garg. Scalar (V/f) control of 3-phase induction motors. Application report. SPRABQ8.- Dallas, USA.:Texas Instruments
Библиографический список
13.
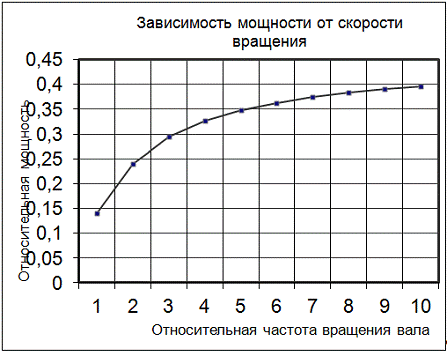2 Свойства волн: скорость, амплитуда, частота и период — физикаРаздел Цели обучения
К концу этого раздела вы сможете делать следующее:
- Определять амплитуду, частоту, период, длину волны и скорость волны
- Связь частоты волны, периода, длины волны и скорости
- Решение задач, связанных со свойствами волн
Поддержка учителей
Поддержка учителей
Цели обучения в этом разделе помогут вашим учащимся освоить следующие стандарты:
- (7) Научные понятия. Учащийся знает характеристики и поведение волн. Ожидается, что студент:
- (Б) исследовать и анализировать характеристики волн, включая скорость, частоту, амплитуду и длину волны, и рассчитывать, используя взаимосвязь между скоростью волны, частотой и длиной волны;
- (Д)
исследовать поведение волн, включая отражение, преломление, дифракцию, интерференцию, резонанс и эффект Доплера.
Основные термины раздела
| длина волны | скорость волны |
Поддержка учителей
Поддержка учителей
[BL][OL][AL] Проверьте амплитуду, период и частоту для простого гармонического движения.
Волновые переменные
В главе о движении в двух измерениях мы определили следующие переменные для описания гармонического движения:
- Амплитуда — максимальное смещение от положения равновесия объекта, колеблющегося вокруг такого положения равновесия
- Частота — количество событий в единицу времени
- Период — время, необходимое для совершения одного колебания
Для волн эти переменные имеют одинаковое основное значение. Однако полезно сформулировать определения более конкретным образом, применимым непосредственно к волнам:
- Амплитуда — расстояние между положением покоя и максимальным смещением волны
- Частота — количество волн, проходящих через определенную точку в секунду
- Период — время, необходимое для завершения одного цикла волны
Волны характеризуют не только амплитуда, частота и период, но и их длина волны и скорость волны.
Длина волны λλ — это расстояние между соседними одинаковыми частями волны, параллельными направлению распространения. Скорость волны vwvw — это скорость, с которой движется возмущение.
Советы для успеха
Скорость волны иногда также называют скоростью распространения или скоростью распространения , поскольку возмущение распространяется из одного места в другое.
Рассмотрим периодическую волну воды на рис. 13.7. Его длина волны — это расстояние от гребня до гребня или от впадины до впадины. Длину волны также можно рассматривать как расстояние, пройденное волной за один полный цикл или один период. Время одного полного движения вверх-вниз равно периоду простой водной волны Т . На рисунке сама волна движется вправо со скоростью волны v w . Его амплитуда X — это расстояние между положением покоя и максимальным смещением — либо гребнем, либо впадиной — волны.
Важно отметить, что это движение волны на самом деле является возмущением , движущимся вправо, а не самой водой; в противном случае птица двигалась бы вправо. Вместо этого чайка качается вверх и вниз на месте, когда под ней проходят волны, преодолевая в общей сложности расстояние 2,9 м.0077 X за один цикл. Однако, как упоминалось в текстовой статье о серфинге, настоящие океанские волны более сложны, чем этот упрощенный пример.
Рисунок 13,7 Волна имеет длину волны λ , что является расстоянием между соседними одинаковыми частями волны. Возмущение поверхности вверх-вниз распространяется параллельно поверхности со скоростью v w .
Смотреть физику
Амплитуда, период, частота и длина волны периодических волн
Данное видео является продолжением видео «Введение в волны» из раздела «Виды волн». В нем обсуждаются свойства периодической волны: амплитуда, период, частота, длина волны и скорость волны.
Советы для успеха
Гребень волны иногда также называют пиком .
Смотреть Физика: амплитуда, период, частота и длина волны периодических волн. В этом видео представлены несколько концепций звука; амплитуда, период, частота и длина волны периодических волн.Нажмите, чтобы просмотреть содержимое
Если вы находитесь на лодке в ложбине волны в океане, и амплитуда волны составляет 1\,\text{м}, какова высота волны с вашего местоположения?
1\,\текст{м}
2\,\текст{м}
4\,\текст{м}
8\,\текст{м}
Взаимосвязь между частотой волны, периодом, длиной волны и скоростью
Поскольку частота волны — это количество волн в секунду, а период — это, по сути, количество секунд на волну, соотношение между частотой и периодом составляет
f=1Tf=1T13,1
или
T=1f,T=1f,13,2
так же, как и в случае гармонического движения объекта.
Из этого соотношения видно, что более высокая частота означает более короткий период. Напомним, что единицей измерения частоты является герц (Гц), а 1 Гц — это один цикл — или одна волна — в секунду.
Скорость распространения v w — это расстояние, которое волна проходит за заданное время, которое составляет одну длину волны за время одного периода. В форме уравнения это записывается как
vw=λTvw=λT13,3
или
vw=fλ.vw=fλ.13,4
Из этого соотношения мы видим, что в среде, где v w постоянно, чем выше частота, тем меньше длина волны. См. рисунок 13.8.
Рисунок
13,8
Поскольку в данной среде они распространяются с одинаковой скоростью, низкочастотные звуки должны иметь большую длину волны, чем высокочастотные звуки. Здесь низкочастотные звуки излучаются большим динамиком, называемым низкочастотным динамиком, а высокочастотные звуки излучаются маленьким динамиком, называемым твитером.
Поддержка учителей
Поддержка учителей
[BL] Для звука более высокая частота соответствует более высокому тону, а более низкая частота соответствует более низкому тону. Амплитуда соответствует громкости звука.
[BL][OL] Поскольку звук на всех частотах имеет одинаковую скорость в воздухе, изменение частоты означает изменение длины волны.
[Поддержка рисунка] Один и тот же динамик способен воспроизводить как высокочастотные, так и низкочастотные звуки. Однако высокие частоты имеют более короткую длину волны и, следовательно, лучше всего воспроизводятся динамиком с маленьким, твердым и плотным диффузором (твитер), тогда как более низкие частоты лучше всего воспроизводятся с большим и мягким диффузором (вуфер).
Эти фундаментальные соотношения справедливы для всех типов волн. Например, для волн на воде v w — это скорость поверхностной волны; для звука v w — скорость звука; а для видимого света v w — это скорость света.
Амплитуда X совершенно не зависит от скорости распространения v w и зависит только от количества энергии в волне.
Снап Лаборатория
Волны в миске
В этой лаборатории вы проведете измерения, чтобы определить, как на амплитуду и период волн влияет передача энергии от пробки, брошенной в воду. Пробка изначально обладает некоторой потенциальной энергией, когда ее держат над водой — чем больше высота, тем выше потенциальная энергия. Когда пробка падает, такая потенциальная энергия преобразуется в кинетическую энергию, когда пробка падает. Когда пробка ударяется о воду, эта энергия распространяется по воде волнами.
- Большая миска или таз
- Вода
- Пробка (или мячик для пинг-понга)
- Секундомер
- Рулетка
Инструкции
Процедура
- Наполните большую миску или таз водой и подождите, пока вода не осядет, чтобы не было ряби.
- Аккуратно бросьте пробку в середину чаши.
- Оцените длину волны и период колебаний водной волны, распространяющейся от пробки. Вы можете оценить период, подсчитав количество ряби от центра к краю чаши, пока ваш партнер измеряет это время. Эта информация в сочетании с измерением чаши даст вам длину волны при использовании правильной формулы.
- Выньте пробку из миски и подождите, пока вода снова не осядет.
- Аккуратно бросьте пробку с высоты, отличной от высоты первого падения.
- Повторите шаги с 3 по 5, чтобы собрать второй и третий наборы данных, сбрасывая пробку с разной высоты и записывая полученные длины волн и периоды.
- Интерпретируйте свои результаты.
Пробка падает в бассейн с водой, создавая волны. Зависит ли длина волны от высоты над водой, с которой брошена пробка?
Нет, влияет только на амплитуду.
Да, длина волны затронута.
Поддержка учителей
Поддержка учителей
Учащиеся могут заранее измерить чашу, чтобы лучше оценить длину волны.
Виртуальная физика
Волна на струне
В этой анимации посмотрите, как струна вибрирует в замедленном темпе, выбрав параметр «Замедленное движение». Выберите параметры «Без конца» и «Вручную» и покачивайте конец струны, чтобы создавать волны самостоятельно. Затем переключитесь на настройку Oscillate для автоматического создания волн. Отрегулируйте частоту и амплитуду колебаний, чтобы увидеть, что произойдет. Затем поэкспериментируйте с регулировкой демпфирования и натяжения.
Проверка захвата
Какая из настроек — амплитуда, частота, затухание или натяжение — изменяет амплитуду волны при ее распространении? Что он делает с амплитудой?
- Частота; он уменьшает амплитуду волны по мере ее распространения.
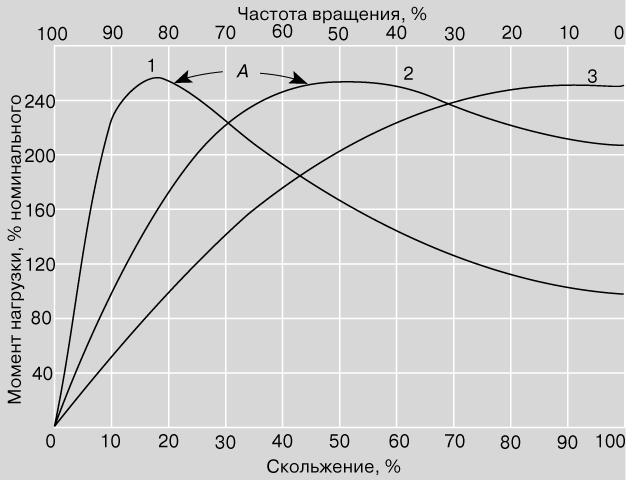
- Частота; он увеличивает амплитуду волны по мере ее распространения.
- Демпфирование; он уменьшает амплитуду волны по мере ее распространения.
- Демпфирование; он увеличивает амплитуду волны по мере ее распространения.
Решение волновых задач
Рабочий пример
Рассчитайте скорость распространения волн: Чайка в океане
Рассчитайте скорость морской волны на предыдущем рисунке, если расстояние между гребнями волн равно 10,0 м, а время, за которое чайка качается вверх и вниз, составляет 5,00 с.
Стратегия
Заданы значения длины волны (λ=10,0 м)(λ=10,0 м) и периода (T=5,00 с)(T=5,00 с), и нас просят найти vwvw Следовательно, мы можем использовать vw= λTvw=λT, чтобы найти скорость волны.
Решение
Введите известные значения в vw=λTvw=λT
vw=10,0 м5,00 с=2,00 м/с.vw=10,0 м5,00 с=2,00 м/с. 13.
5
Обсуждение
Такая низкая скорость кажется приемлемой для океанской волны. Обратите внимание, что на рисунке волна движется вправо с этой скоростью, которая отличается от переменной скорости, с которой чайка качается вверх и вниз.
Рабочий пример
Вычислите период и скорость волны игрушечной пружины.
Женщина на рис. 13.3 создает две волны каждую секунду, встряхивая игрушечную пружину вверх и вниз. а) Каков период каждой волны? (b) Если каждая волна проходит 0,9 метра после одного полного волнового цикла, какова скорость распространения волны?
Стратегия ЗА (А)
Чтобы найти период, мы решаем T=1fT=1f, учитывая значение частоты (f=2s−1).(f=2s−1).
Решение для (a)
Введите известное значение в T=1fT=1f
T=12 с-1=0,5 с. T=12 с-1=0,5 с.13,6
Стратегия ЗА (Б)
Поскольку одним из определений длины волны является расстояние, пройденное волной за один полный цикл или один период, приводятся значения длины волны (λ=0,9 м)(λ=0,9 м), а также частоты.
Следовательно, мы можем использовать vw=fλvw=fλ, чтобы найти скорость волны.
Решение для (b)
Введите известные значения в vw=fλvw=fλ
vw=fλ=(2 с-1)(0,9 м) = 1,8 м/с. vw=fλ=(2 с-1)(0,9 м) = 1,8 м/с.
Обсуждение
Мы могли бы также использовать уравнение vw=λTvw=λT для определения скорости волны, поскольку мы уже знаем значение периода (T=0,5 с)(T=0,5 с) из нашего расчета в части ( а), и мы бы пришли к тому же ответу.
Практические задачи
7.Частота волны 10 Гц. Каков его период?
- Период волны 100 с.
- Период волны 10 с.
- Период волны 0,01 с.
- Период волны 0,1 с.
Какова скорость волны с длиной волны 2 м и частотой 5 Гц?
- 20 м/с
- 2,5 м/с
- 0,4 м/с
- 10 м/с
Проверьте свое понимание
Поддержка учителей
Поддержка учителей
Используйте эти вопросы, чтобы оценить достижения учащихся в соответствии с целями обучения данного раздела.
Если учащиеся борются с определенной целью, эти вопросы помогут определить такую цель и направить их к соответствующему содержанию.
Какова амплитуда волны?
- Четверть общей высоты волны
- Половина общей высоты волны
- Удвоенная общая высота волны
- Четырехкратная общая высота волны
Что понимают под длиной волны?
Длина волны — это расстояние между соседними одинаковыми частями волны, параллельными направлению распространения.
Длина волны — это расстояние между соседними одинаковыми частями волны, перпендикулярное направлению распространения.
Длина волны — это расстояние между гребнем и прилегающей впадиной волны, параллельное направлению распространения.
- 92
Когда длина волны прямо пропорциональна периоду волны?
- Когда скорость волны уменьшается вдвое
- Когда скорость волны постоянна
- Когда скорость волны удваивается
- Когда скорость волны утроится
Чем скорость отличается от частоты
Частота в физике
Частота — это мера того, как часто что-то происходит, а скорость — это мера того, насколько быстро что-то движется. Другими словами, частота говорит вам, сколько раз что-то происходит за данный период, а скорость говорит вам, какое расстояние что-то преодолевает за этот же период. Скорость всегда измеряется относительно какого-либо другого объекта или величины; например, мы можем измерить скорость автомобиля в километрах в час (км/ч) или скорость света в метрах в секунду (м/с).
Интересно, что эти два понятия связаны: чем выше частота чего-либо, тем выше будет его скорость. Например, если мы сравним два объекта, которые оба движутся со скоростью 1 м/с, но один имеет частоту 1 Гц, а другой — 2 Гц, то второй объект движется в два раза быстрее, чем первый. Это потому, что он преодолевает вдвое большее расстояние за то же время.
Частота — это мера того, как часто что-то происходит, а скорость — это мера того, насколько быстро что-то движется. Эти две концепции связаны тем, что чем выше частота чего-либо, тем выше будет его скорость.
Разница между частотой и скоростью
Разница между скоростью и частотой заключается в том, что частота — это мера того, как часто что-то происходит, а скорость — это мера того, насколько быстро что-то движется.
Единица скорости в физике
В физике единицей скорости является метр в секунду (м/с). Единицей частоты является герц (Гц). Один Гц равен одному циклу в секунду.
В чем разница между скоростью звука и частотой звука
Разница между скоростью звука и частотой звука заключается в том, что скорость звука — это скорость, с которой звуковые волны распространяются через среду, в то время как частота звука — это количество колебаний звуковой волны в секунду.
На скорость звука влияют свойства среды, в которой он распространяется; например, звук распространяется медленнее через более плотные материалы, такие как вода или металл. Частота звука, с другой стороны, определяется источником звука. Например, камертон воспроизводит звук с очень определенной частотой, тогда как человеческий голос может воспроизводить диапазон частот.
Обычно низкочастотные звуки слышны хуже, чем высокочастотные. Вот почему мы часто слышим более высокие звуки, такие как собачий свист, но не более низкие звуки, такие как грохот грузовиков.
В чем разница между скоростью и частотой света
Разница между скоростью и частотой света заключается в том, что скорость света — это скорость, с которой световые волны проходят через среду, а частота света — это количество колебаний в секунду световой волны.