Зависимость давления от температуры: Зависимость температуры кипения воды от давления

Глава 13. Газовые законы

Задачи на газовые законы часто предлагаются школьникам на едином государственном экзамене. Для решения этих задач вполне достаточно знать уравнение состояния идеального газа (закон Клапейрона-Менделеева) и уметь использовать его алгебраически и геометрически (для построения графиков зависимости одних параметров газа от других) в простейших ситуациях. Кроме того, нужно понимать, как описываются смеси идеальных газов (закон Дальтона).

Уравнение, связывающее параметры газа друг с другом, называется уравнением состояния. Для идеального газа, взаимодействие молекул которого мало, уравнение состояния имеет вид

(13.1)

где — давление газа, — концентрация молекул газа (число молекул в единице объема), — постоянная Больцмана, — абсолютная (в шкале Кельвина) температура. Учитывая, что , где — число молекул газа, — объем сосуда, в котором находится газ (часто говорят объем газа), получим из (13.

1)

(13.2)

Число молекул можно связать с количеством вещества газа : , где — число Авогадро. Поэтому формулу (13.2) можно переписать в виде

(13.2)

где произведение постоянных Авогадро и Больцмана обозначено как . Постоянная = 8,31 Дж/(К•моль) называется универсальной газовой постоянной. Количество вещества газа можно также выразить через его массу и молярную массу этого газа

(13.3)

С учетом (13.3) закон (13.2) можно переписать и в таком виде

(13.4)

Уравнение состояния идеального газа (13.1)-(13.4), которое также называется уравнением (или законом) Клапейрона-Менделеева, позволяет связывать параметры идеального газа и проследить за их изменением в тех или иных процессах.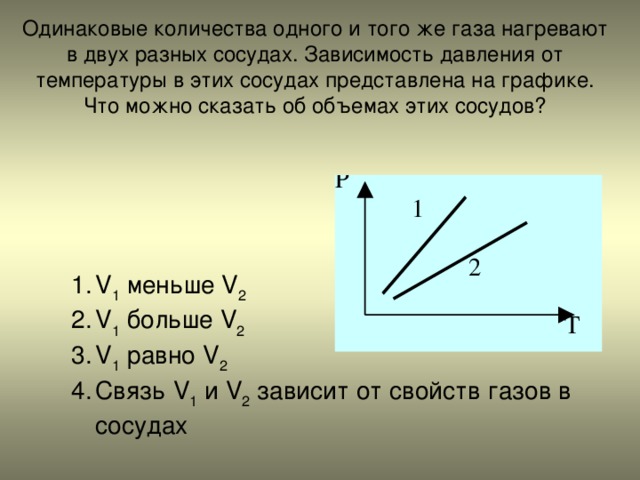

В школьном курсе физики рассматриваются три изопроцесса, в которых один из трех параметров газа (давление, температура и объем) не изменяется. В изобарическом процессе не изменяется давление газа, в изотермическом — температура, в изохорическом — объем. Изопроцессам отвечают следующие графики зависимости давления от объема, давления от температуры, объема от температуры.

Для изобарического процесса

Первые два графика очевидны. Последний получается так. Из закона Клапейрона-Менделеева следует, что зависимость объема от температуры при постоянном давлении имеет вид

(13.5)

где — постоянная. Графиком функции (13.5) является прямая, продолжение которой проходит через начало координат.

Для изохорического процесса

Второй график следует из соотношения

(13. 6)

где — постоянная при постоянном объеме.

Для изотермического процесса

Первый график следует из закона Клапейрона-Менделеева, который при постоянной температуре газа можно привести к виду

(13.7)

где — постоянная. Отсюда следует, что графиком зависимости от в изотермическом процессе является гипербола.

Важнейшее свойство уравнения состояния идеального газа (13.1)-(13.4) заключается в том, что «индивидуальность» газа никак не проявляется в этих законах — единственный параметр собственно газа, входящий в уравнение состояния, — это число молекул. Например, 1 моль гелия и 1 моль азота, находящиеся в одинаковых объемах и имеющие одинаковые температуры, оказывают одинаковое давление. Отсюда следует, что и давление смеси идеальных газов определяется суммарным числом молекул всех компонент смеси:

(13. 8)

где — число молекул первой, второй, третьей и т.д. компонент смеси, — постоянная Больцмана, — абсолютная температура смеси, — объем сосуда. Величины , имеющие смысл давления каждой компоненты смеси при условии, что она имела бы такую же температуру и занимала бы весь объем, называются парциальными давлениями компонент. Закон (13.8) называется законом Дальтона. Рассмотрим теперь в рамках этих законов предложенные выше задачи.

В задаче 13.1.1 из уравнения состояния в форме (13.1), получаем для давления в конце процесса :

т.е. давление газа увеличилось в 6 раз (ответ 1).

Применяя закон Клапейрона-Менделеева (13.2) к первому и второму газам (задача 13.1.2), получаем

где — искомый объем. Сравнивая первую и вторую формулы, заключаем, что (ответ 1).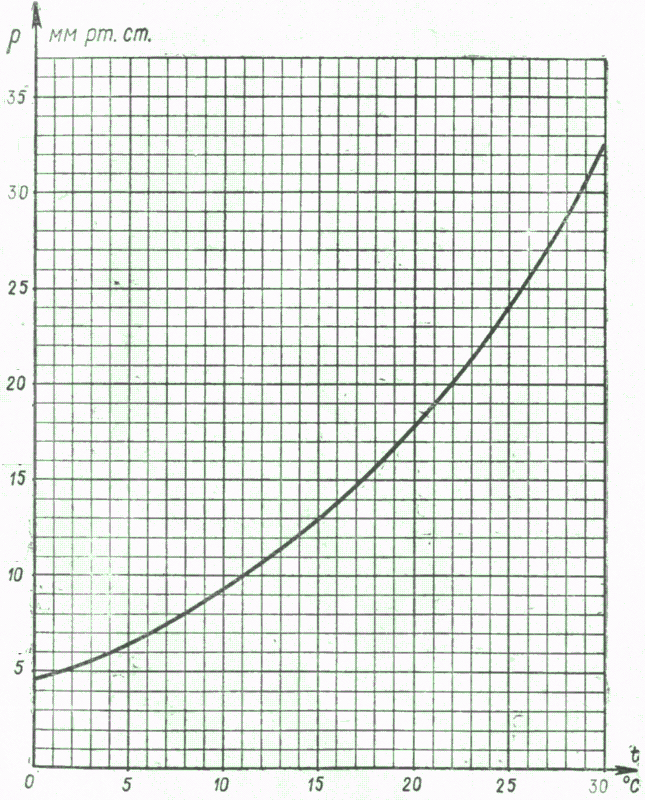

Закон Клапейрона-Менделеева для газа в начальном и конечном состояниях (задача 13.1.3) дает

где — неизвестная температура. Из сравнения этих формул получаем , т.е. температуру газа в сосуде нужно повысить вдвое (ответ 2).

Из закона Клапейрона-Менделеева для начального и конечного состояний газа в задаче 13.1.4 имеем

Отсюда , т.е. количество вещества газа в сосуде увеличилось в 1,25 раза (ответ 3).

Первым, кто понял, почему жидкость поднимается вместе с трубкой (задача 13.1.5), и почему «природа боится пустоты» (Аристотель), но только до определенного предела, был знаменитый итальянский физик, современник Г. Галилея Э. Торричелли. Давайте рассмотрим рассуждения Торричелли подробно. Основная идея Торричелли заключалась в том, что атмосферный воздух оказывает давление на все поверхности, с которыми он контактирует. В равновесии жидкость занимает такое положение, чтобы все воздействия на каждый ее элемент компенсировались. Если бы трубка была открыта (см. левый рисунок), то жидкость не поднялась бы в трубке. Действительно, в этом случае на бесконечно малый элемент жидкости в трубке около поверхности (выделен на рисунке) действовали бы сила со стороны атмосферного воздуха в трубке, направленная вниз. С другой стороны, атмосферный воздух действует и на остальную поверхность жидкости, и это воздействие благодаря закону Паскаля передается выделенному элементу жидкости в трубке снизу. Таким образом, воздействие воздуха на поверхность жидкости в трубке и на свободную поверхность жидкости компенсируют друг друга, если уровень жидкости в трубке совпадает с уровнем жидкости в остальном сосуде. Если же мы поднимаем трубку, выпустив из нее воздух, на рассматриваемый элемент жидкости воздух сверху не действует (его нет в трубке), поэтому воздействие воздуха на свободную поверхность жидкости приведет к тому, что жидкость войдет в трубку и заполнит ее.

При вытаскивании трубки жидкость будет подниматься вслед за ней. Однако при дальнейшем поднятии трубки наступит такой момент, когда воздействие воздуха на свободную поверхность и столба жидкости в трубке сравняются (в этот момент атмосферное давление будет равно гидростатическому давлению жидкости в трубке на уровне свободной поверхности). Дальнейший подъем трубки уже не приведет к поднятию жидкости — атмосферное давление не сможет «держать» столб жидкости большей высоты. Для воды этот столб составляет около 10 м, для ртути, с которой и экспериментировал Э. Торричелли, — 76 сантиметров. Таким образом, жидкость в трубке поднимается благодаря давлению атмосферного воздуха на поверхность воды в сосуде и закону Паскаля (ответ 4).

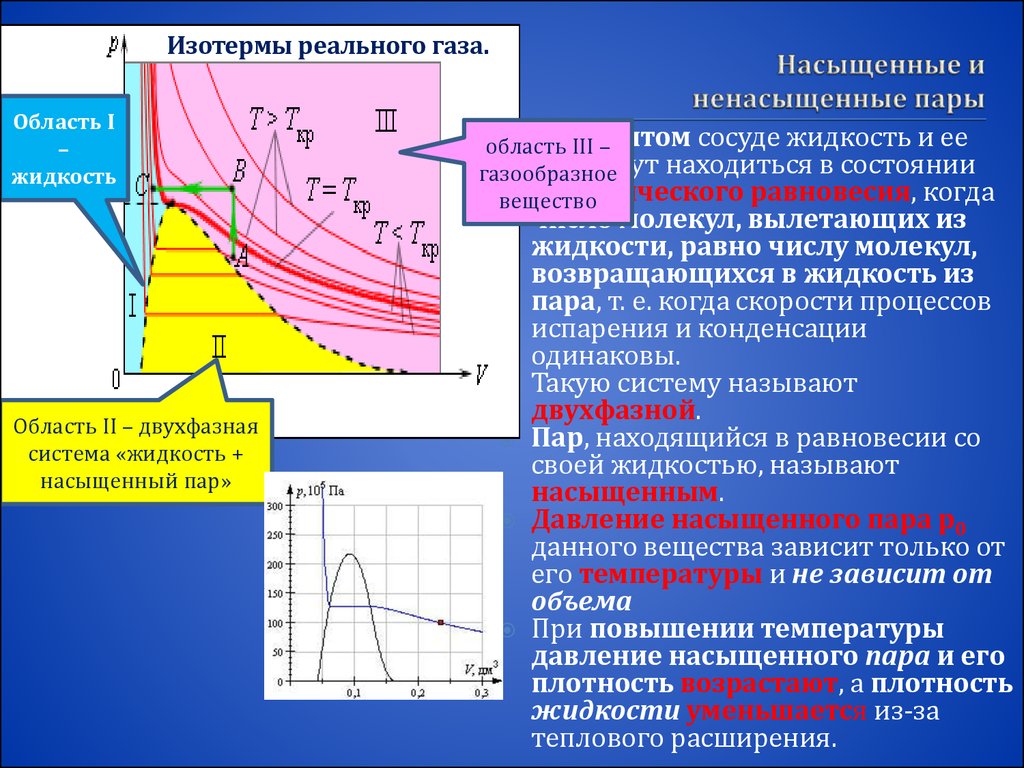
Сравнивая графики процессов 1, 2, 3 и 4, данные в условии задачи 13.1.6, с графиками изопроцессов, приведенными во введении к настоящей главе, заключаем, что: процесс 1 — изотермический, 2 — изохорический, 3 — изобарический. В процесс 4 меняются и давление, и объем, и температура газа (ответ 4).

В изотермическом процессе давление зависит от объема как ; на диаграмме этот процесс изображается гиперболой. Поэтому изотермическими являются процессы 1 и 3 (задача 13.1.7), но в процессе 1 объем газа убывает. Следовательно, изотермическим расширением является процесс 3 (ответ 3).

Изохорическим охлаждением в задаче 13.1.8 является процесс 4 (см. рисунок) В двух последних задачах этого варианта нужно с помощью закона Клапейрона-Менделеева вычислить один из параметров газа, если даны остальные параметры. В задаче 13.1.9 из закона Клапейрона-Менделеева

получим

(ответ 1).

В задаче 13.1.10 при вычислениях следует не забыть перевести температуру газа в Кельвины.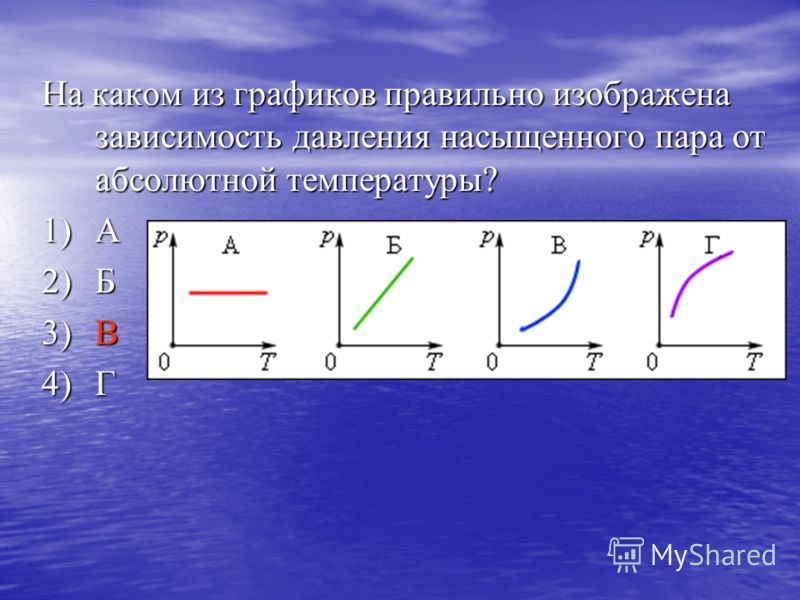 Из закона Клапейрона-Менделеева находим

(ответ 1).

Из уравнения состояния в форме (13.2) следует, что при одинаковых объемах и температурах давление идеального газа определяется только полным числом молекул. Поэтому отношение давления водорода и гелия в задаче 13.2.1 равно 2 (ответ 2).

Поскольку перегородка в задаче 13.2.2 подвижная и находится в равновесии, давления газа в отсеках сосуда слева и справа от перегородки равны. Применяя к ним при этом условии закон Клапейрона-Менделеева, получим

для гелия

для азота

где температуры и массы газов по условию одинаковы. Деля эти уравнения друг на друга, находим отношение объемов частей сосуда

(ответ 4).

Если бы точки, отвечающие состояниям 1 и 2 в задаче 13. 2.3, лежали на одной прямой, продолжение которой проходит через начало координат, то эти состояния принадлежали бы одной и той же изохоре, и, следовательно, объем газа в этих состояниях был одинаковым (см. формулу (13.6)). Поэтому для сравнения объемов этих состояний построим изохоры, проходящие через точки 1 и 2, и сравним отвечающие им объемы (см. рисунок; изохоры, проходящие через точки 1 и 2, показаны пунктиром).

Из формулы (13.6) следует, что чем больше объем, тем меньше коэффициент перед в зависимости (13.6), и, следовательно, меньше наклон соответствующей изохоры к оси температур. Поэтому изохоре 1 отвечает больший объем, чем изохоре 2, и, следовательно, объем газа в процессе 1-2 уменьшается (ответ 2).

Аналогичные рассуждения в задаче 13.2.4 показывают, что наибольшему давлению отвечает изобара, проходящая через точку (поскольку соответствующая прямая имеет наименьший наклон к оси температур; см. рисунок ниже). Поэтому правильный ответ в этой задаче — 3.

В закон Клапейрона-Менделеева входит абсолютная температура газа, поэтому данные в задаче 13.2.5 значения нужно перевести в Кельвины. В результате для отношения давлений газа в конечном и начальном состояниях получаем

(ответ 4).

Как следует из опыта, при приведении тел в тепловой контакт выравниваются их температуры. Это же касается и частей одного тела или даже компонент смеси газов (задача 13.2.6). Поэтому температуры компонент смеси будут одинаковы (ответ 1). Что касается парциальных давлений, плотностей или концентрации компонент смеси, то их значения зависят от количества молекул каждой компоненты смеси и могут быть различны.

Парциальное давление компонент смеси – это давление, которое оказывают только молекулы каждой компоненты. Как следует из формулы (13.8) парциальное давление любой компоненты можно найти, применяя только к ней закон Клапейрона-Менделеева и считая, что она имеет такую же температуру, как и вся смесь, и занимает такай же объем, как и вся смесь газов. Поэтому отношение парциальных давлений отдельных компонент смеси равно отношению количеств вещества (или числа молекул) этих компонент. Поэтому для отношения парциальных давлений углекислого газа и гелия в сосуде в задаче 13.2.7 имеем (ответ 2).

Как следует из закона Дальтона, давление смеси газов определяется полным количеством молекул в ней. Поэтому для анализа изменения давления смеси газов при протекании в ней химической реакции (задача 13.2.8) необходимо исследовать изменение числа молекул. Гелий не участвует в химической реакции — один моль гелия был и в начальном, и в конечном состоянии смеси. С озоном происходила реакция

т.е. из двух молекул озона в результате реакции получились три молекулы кислорода. Поэтому два моля озона превратились в три моля кислорода, и общее количество вещества смеси стало равно четырем молям. Поэтому давление смеси увеличивается в 4/3 раза (ответ 2).

Поскольку объемы и температуры газов одинаковы (задача 13.2.9), для сравнения их давлений необходимо сравнить число молекул в них. По условию в одном сосуде находится один моль азота, в другом 1 г водорода (т.е. половина моля) и 3 • 10²³ молекул гелия (тоже половина моля). Поэтому и в одном и в другом сосуде находятся одинаковые количества молекул, и, следовательно, давление газов в них одинаково (ответ 3).

Плотность газа (задача 13.2.10) можно найти из следующей цепочки формул

(ответ 4). Здесь — масса газа, — масса одной молекулы газа.

Зависимость давления в колесах велосипедов, мотоциклов, автомобилей от температуры

Подробно о давлении в шинах велосипеда описано в отдельной статье на нашем сайте: «Давление в велосипедных шинах».

Здесь же мы обсудим только один нюанс: влияние температуры на давление в накачанном колесе. Причем это влияние имеет одинаковую природу и последствия для любых шин – велосипедных, мопедных, мотоциклетных и автомобильных.

От чего зависит температура воздуха в покрышке?

Прежде всего от температуры воздуха окружающей среды, где находится велосипед, (мотоцикл, автомобиль) при стоянке. Т.е. если колеса накачаны до давления 2,5 атмосферы дома или в гараже, где температура 20 °С, а затем байк (мотоцикл, автомобиль) выезжает на улицу, где температура +30 °С, то давление в шине уже чуть-чуть поднимается.

Далее. Колеса начинают катиться по горячему асфальту и соответственно нагреваются от соприкосновения с самим асфальтом и от возникающей силы трения резины об асфальт. В результате давление опять поднимается. Конечно, на велосипеде нагревание от трения заметно очень и очень мало и волнует только больших профессионалов на гонках, но при большом перепаде температур – в сильную жару или в холод это уже становится заметно. Этот фактор (нагрев от трения резины об асфальт) для автомобилистов и мотоциклистов гораздо важнее – скорости там значительно больше, чем на велосипеде и, соответственно, сила трения то же.

Нельзя сказать, что этот вопрос критически важен, но учитывать его нужно и особенно это заметно при значительных перепадах: более 15-20 градусов.

Например, если велосипед хранится зимой в теплой квартире или отапливаемом гараже при температуре +20 – +25 °С, а кататься Вы выезжаете зимой на -10 °С, то перепад составляет 30-35 градусов. Едет велосипед по снегу, снежной корке или льду, холодному замёрзшему асфальту, у которого температура то же не +20, и в итоге давление в колесе уменьшается примерно на 0,3 bar. А это уже значительно.

Как рассчитать давление в колесе в зависимости от температуры?

Мы не будем глубоко вдаваться в физику процесса.

Это все объясняет закон Шарля (второй закон Гей-Люссака), о котором можно почитать в учебниках физики или в википедии.

Приведем его основную идею и формулу для расчета.

Закон Шарля гласит, что «Давление газа фиксированной массы и фиксированного объёма прямо пропорционально абсолютной температуре газа.» В накачанном колесе как раз газ (воздух) фиксированной массы и объёма и чем выше температура – тем выше давление. Зимой на холоде в колесах оно уменьшается, а летом на солнце – увеличивается.

Сама формула рассчета давления в шинах в зависимости от температуры воздуха выглядит следующим образом:

Пример расчета: Если известно давление в колесе при 0°С, например, оно составляет 2,5 атмосферы (bar), то для расчета давления при температуре 25°С используем эту формулу и получаем:

«Давление при 0°С» * (273 + 25) / 273

или

2,5 * (273+25) / 273 = 2,73 ≈ 2,7 bar

Еще раз напомним, что: 273 – это температура в градусах по шкале Кельвина, а не в градусах по Цельсию.

Для облегчения жизни приведем таблицу изменения давления в колесе, накаченном при 0°С, в зависимости от температуры воздуха.

 

Если Вы измеряли давление при +20°С и хотите понять какое оно станет зимой на улице при температуре -15°С, то формула примет вид:

2,5 * (273 + -15) / (273 + 20)  = 2,5 * 258 / 293 = 2,2 bar

В общем случае, если считать очень грубо и приблизительно, то можно сказать, что при давлении более 2 bar изменение температуры на каждые 8-10 °С приводит к изменению давления примерно на 0,1 Bar.

Опять, же для удобства приведем таблицу быстрого получения значений давления в колесе в зависимости от температуры воздуха на улице, в случае, если байкер накачивал его дома, при +20 °С.

Изменение давления особенно нужно учитывать в случаях, если шины накачиваются летом в домашних условиях до давления близкого к максимальному и поездка предстоит по жаре или наоборот, колеса качаются близко до минимальных значений, а поездка предстоит по холоду. Главное, чтобы не выйти за пределы минимальных и максимальных значений, указанных на покрышке.

Эта таблица работает так же для мотоциклетных и автомобильных колес. Даже если их накачивают гелием. Гелий ведь то же газ и так же подчиняется всем законам физики, несмотря на то, что об этом говорят работники СТО.

Связь между давлением и температурой

24 апреля 2018 г.

от Lakna

Чтение через 4 мин.

Связь между давлением и температурой газа определяется законом Гей-Люссака о давлении и температуре.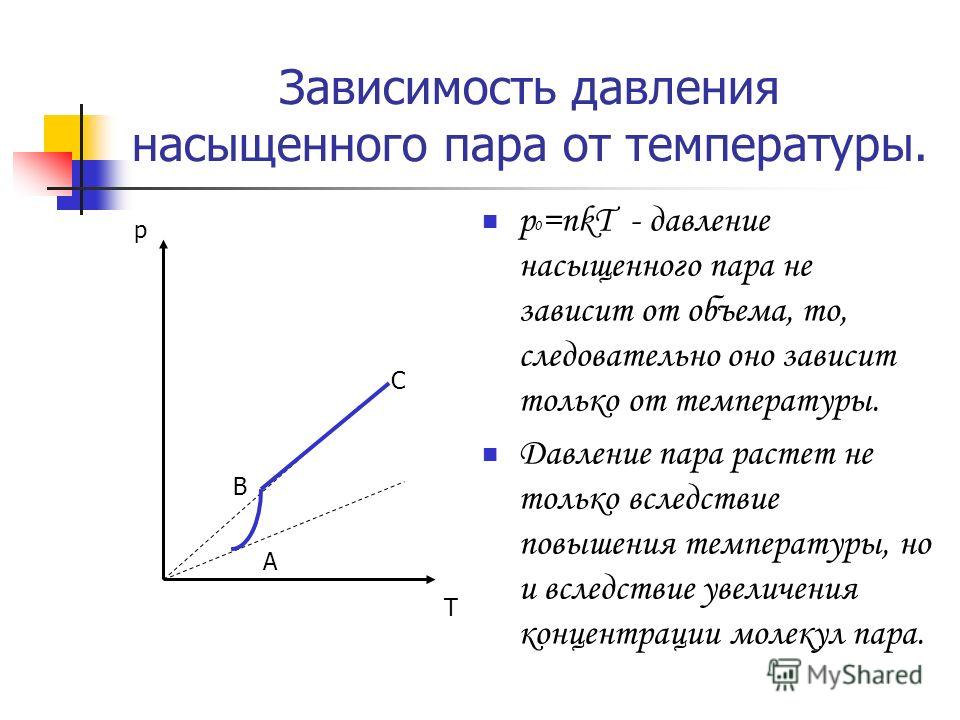 Этот закон гласит, что давление (P) фиксированной массы газа при постоянном объеме прямо пропорционально его температуре по Кельвину (T). Следовательно, когда давление в конкретной системе повышается, температура этой системы также повышается, и наоборот. Газовые законы описывают поведение газов в зависимости от давления, объема, температуры и количества. Газы — одно из состояний вещества, либо очень сильно сжатое, либо расширенное, чтобы заполнить большое пространство.

Ключевые области, покрываемые

1. Каково давление
— Определение, давление газа
2. Какова температура
— Определение, измерение
. Температура
     – Закон Гей-Люссака

Ключевые термины: газ, закон Гей-Люссака, Кельвин, давление, температура в контакте с ним. Он рассчитывается как сила, приходящаяся на единицу площади. Когда рассматривается закрытая газовая камера, окруженная вакуумом, давление, оказываемое газом на стенки камеры, зависит от трех факторов. Это количество газа в камере, объем камеры и температура газа. Когда другие параметры постоянны, давление внутри камеры прямо пропорционально количеству газа в камере; обратно пропорциональна объему камеры; она прямо пропорциональна температуре газа внутри камеры. Давление определяется в Рисунок 1.

Рисунок 1: Давление

Атмосферное давление создается весом воздуха над нами. На уровне моря это 10 ⁵ Па.

Что такое температура

Температура – ​​это степень нагревания вещества или объекта. Он представляет собой внутреннюю энергию, содержащуюся в конкретной системе. Температуру можно измерить термометром, который откалиброван в различных единицах измерения. Шкала Цельсия является наиболее широко используемой шкалой для измерения температуры, которая обозначается в °C. Единицей измерения температуры в Международной системе единиц (СИ) является кельвин (К). Термометр изображен на рисунок 2.

Рисунок 2: Термометр

При самой низкой теоретической температуре, равной абсолютному нулю, тепловое движение частиц в веществе минимально. Абсолютный ноль равен 0 К, а это -273,14 °С.

Какая связь между давлением и температурой

Связь между давлением и температурой описывается применительно к газам. Закон Гей-Люссака — это газовый закон, описывающий зависимость давления от температуры. В нем говорится, что при постоянном объеме давление данного количества определенного газа прямо пропорционально его температуре по Кельвину. Можно записать так:

• П ∝ Т или
• P/T = k, где k — константа, или
• P ₁ /T ₁ = P ₂ /T ₂

Рисунок 3: Зависимость между давлением и температурой

При повышении температуры в конкретной системе молекулы газа движутся быстрее, оказывая большее давление на стенки газового баллона. Это в плане увеличивает давление в системе. Если температура системы снижается, давление падает. Следовательно, при постоянном объеме давление конкретного газа прямо пропорционально температуре.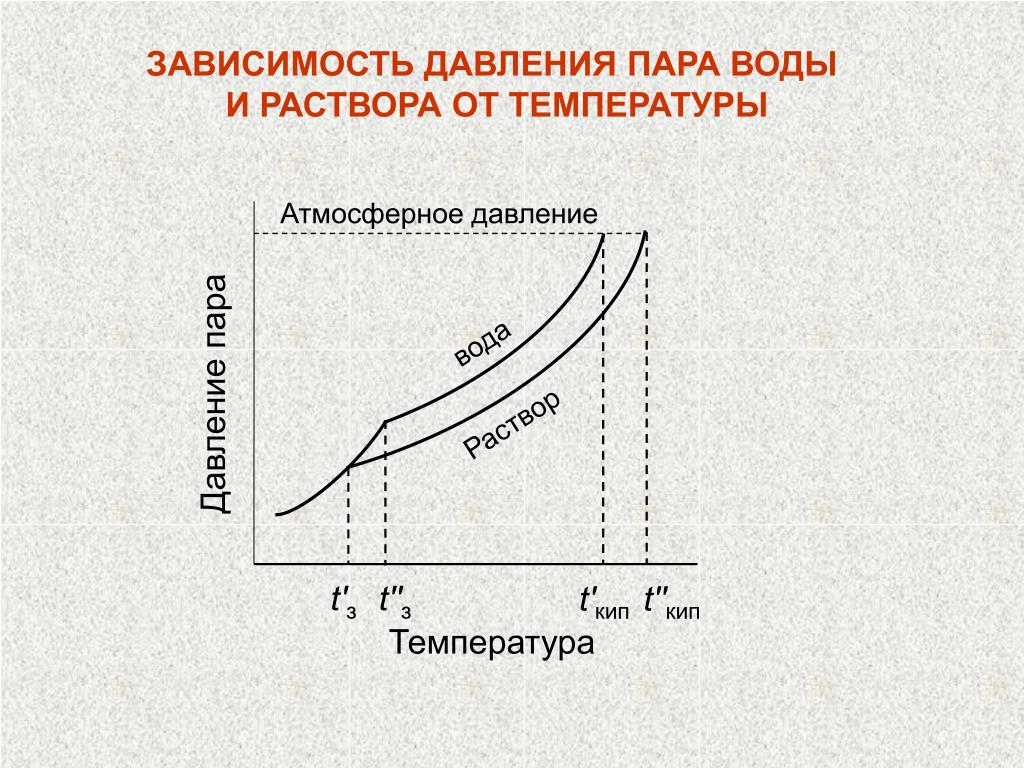

Заключение

Давление данного количества газа прямо пропорционально температуре данного объема. При повышении температуры в системе повышается и давление, и наоборот. Связь между давлением и температурой газа определяется законом Гей-Люссака.

Ссылка:

1. «9.2 Соотношение давления, объема, количества и температуры: закон идеального газа». Химия , Доступно здесь.

Изображение предоставлено:

1. «Площадь силы давления» Клауса-Дитера Келлера — собственная работа (CC BY-SA 3.0) через Commons Wikimedia
2. «1134182» (CC0) через Pixabay

Об авторе: Лакна

Лакна, выпускник факультета молекулярной биологии и биохимии, молекулярный биолог и проявляет большой интерес к открытиям, связанным с природой

Просмотреть все сообщения

Вам также могут понравиться эти

газовых законов

газовых законов

Следующее содержание является содержанием лекции 18. В этой лекции мы рассмотрим газовые законы: Шарля, Бойля, Авагадро и Гей-Люссака, а также законы идеального и комбинированного газа.

 

Законы свойств газа

Существует 4 общих закона, связывающих между собой 4 основных характерных свойства газов. Каждый закон назван по имени его первооткрывателя. Хотя важно понимать отношения, охватываемые каждым законом, знание отправителя не так важно и станет излишним после введения комбинированного закона о газах. Так что сконцентрируйтесь на понимании взаимосвязей, а не на запоминании имен.

Закон Чарльза — дает связь между объемом и температурой , если давление и количество газа поддерживаются постоянными :

1) Если температура газа по Кельвину увеличивается, объем газа увеличивается. (P, n постоянная)
2) Если температура газа по Кельвину уменьшается, объем газа уменьшается. (P, n постоянная)

Это означает, что объем газа прямо пропорционален его температуре по Кельвину. Подумайте об этом так: если вы увеличиваете объем газа и должны поддерживать постоянное давление, единственный способ добиться этого — повысить температуру газа.

Расчеты с использованием закона Чарльза включают изменение либо температуры (T ₂ ), либо объема (V ₂ ) от известного начального количества каждого из них (V ₁ и T ₁ ):

 

Закон Бойля — гласит, что объем данного количества газа при постоянной температуре изменяется обратно пропорционально приложенному давлению, когда температура и масса постоянны.

Уменьшение объема газа означает, что молекулы чаще ударяются о стенки, увеличивая давление, и наоборот, если объем увеличивается, расстояние, которое молекулы должны пройти, чтобы удариться о стенки, увеличивается, и они реже ударяются о стенки, тем самым уменьшая давление. давление.

Как и закон Чарльза, закон Бойля можно использовать для определения текущего давления или объема газа, если известны начальные состояния и одно из изменений:

Закон Авагадро- Определяет соотношение между объемом и количеством газа в молях, когда давление и температура поддерживаются постоянными.

Если количество газа в контейнере увеличивается, объем увеличивается. Если количество газа в сосуде уменьшается, объем уменьшается. Это предполагает, конечно, что контейнер имеет расширяемые стенки.

Отношения снова прямо пропорциональны, поэтому уравнение для расчетов

 

Закон Гей-Люссака гласит, что давление данного количества газа при постоянном объеме прямо пропорционально температуре Кельвина.

 

Если вы нагреваете газ, вы даете молекулам больше энергии, чтобы они двигались быстрее. Это означает большее количество ударов о стенки контейнера и увеличение давления. И наоборот, если вы охладите молекулы, они замедлятся, и давление уменьшится.

Чтобы рассчитать изменение давления или температуры с помощью закона Гей-Люссака, уравнение выглядит следующим образом:

Чтобы немного поиграть с отношениями, попробуйте эту симуляцию.

Закон идеального газа:

Комбинация представленных выше законов порождает закон идеального газа:

Добавление константы пропорциональности, называемой идеальной или универсальной газовой постоянной (R), завершает уравнение.

Как видите, существует множество возможных единиц измерения константы. Единственная постоянная константа заключается в том, что температурная шкала во всем — КЕЛЬВИН.

При использовании закона идеального газа для расчета любого свойства газа вы должны сопоставлять единицы измерения с выбранной вами газовой постоянной, и вы всегда должны указывать свою температуру в градусах Кельвина.

Чтобы использовать уравнение, вам просто нужно определить, чего не хватает в вопросе, и перестроить уравнение, чтобы решить его.

Типичный вопрос был бы задан, поскольку 6,2 литра идеального газа содержатся при 3,0 атм и 37 °C. Сколько из этих молей газа присутствует?

Поскольку единицы газовой постоянной задаются с использованием атмосферы, молей и Кельвина, важно убедиться, что вы конвертируете значения, данные в других шкалах температуры или давления. Для этой задачи переведите температуру в градусах Цельсия в К, используя уравнение:

.

Т = °С + 273

Т = 37 °С + 273
Т = 310 К

Теперь вы можете подставить значения. Решите для количества родинок

н = ПВ/РТ

n = (3,0 атм x 6,2 л) / (0,08206 л атм/моль К x 310 К)
n = 0,75 моль

 

Вот несколько практических задач на использование закона идеального газа: Практика

Закон о комбинированном газе

Выше я сказал, что запоминание всех уравнений для каждого из отдельных газовых законов станет неактуальным после введения последующих законов. Закон, о котором я говорил, — это Закон о комбинированном газе:

Комбинированный газовый закон позволяет вам получить любое из необходимых соотношений, комбинируя все изменяемые части в законе об идеальном газе: а именно: давление, температуру и объем. R и количество молей не фигурируют в уравнении, поскольку они обычно постоянны и, следовательно, сокращаются, поскольку они появляются в равных количествах в обеих частях уравнения.

Как видно выше, уравнение можно решить для любого из входящих в него параметров. Но что еще более важно, вы можете исключить из уравнения все, что останется постоянным.

Например, если в вопросе говорилось, что система при 1 атм и объеме 2 литра претерпела изменение на 3,5 литра, рассчитайте новое давление, вы можете просто исключить температуру из уравнения и получить:

P ₂ = P ₁ V ₁ /V ₂ = (1 атм)(2 л)/3,5 л) = 0,6 атм

Поскольку в вопросе никогда не упоминается температура, мы можем предположить, что она остается постоянной и, следовательно, не учитывается в расчетах. Вы также должны подумать об ответе, который вы получите, с точки зрения того, что вы знаете о газах и о том, как они действуют.