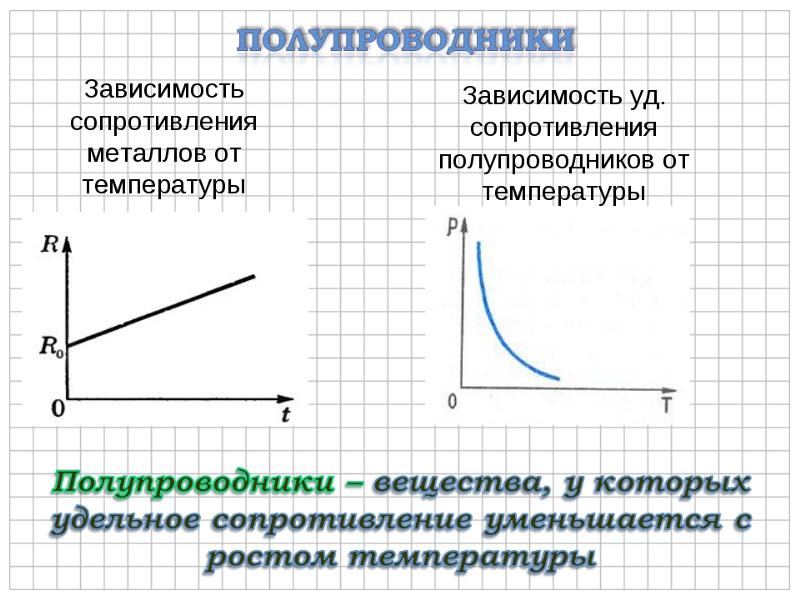
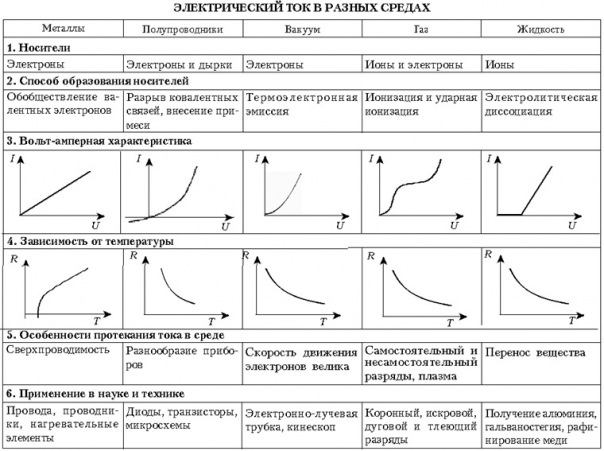
Categories: РазноеAuthor alexxlabPosted on No comment on Зависимость r от r: Зависимость сопротивления R от температуры имеет вид?

Зависимость r от r: Зависимость сопротивления R от температуры имеет вид?

Зависимость сопротивления проводника от температуры

  

Практически в электротехнике выло выявлено, что с увеличением температуры сопротивление проводников из металла возрастает, а с понижением уменьшается. Для всех проводников из металла это изменение сопротивления почти одинаково и в среднем равно 0,4% на 1°С.

Если быть точным, то на самом деле при изменении температуры проводника изменяется его удельное сопротивление, которое имеет следующую зависимость:

 

где ρ и ρ0, R и R0 — соответственно удельные сопротивления и сопротивления проводника при температурах t и 0°С (шкала Цельсия), α — температурный коэффициент сопротивления, [α] = град-1.

Изменение удельного сопротивления проводника приводит к изменения самого сопротивления, что видно из следующего выражения:

 

Зная электронную теорию строения вещества можно дать следующее объяснение увеличению сопротивления металлических проводников с повышением температуры. При увеличении температуры проводник получает тепловую энергию, которая несомненно передается всем атомам вещества, в результате чего .возрастает их тепловое движение. Увеличившееся тепловое движение атомов создает большее сопротивление направленному движению свободных электронов (увеличивается вероятность столкновения свободных электронов с атомами), от этого и возрастает сопротивление проводника.

 С понижением температуры направленное движение электронов облегчается (уменьшается возможность столкновения свободных электронов с атомами), и сопротивление проводника уменьшается. Этим объясняется интересное явление — сверхпроводимость металлов. Сверхпроводимость, т. е. уменьшение сопротивления металлов до нуля, наступает при огромной отрицательной температуре —273° С, называемой абсолютным нулем. При температуре абсолютного нуля атомы металла как бы застывают на месте, совершенно не препятствуя движению электронов.

График звисимости сопротивления металлического проводника от температуры представлен на рисунке 1.

Рисунок 1. График зависимости удельного сопротивления металлического проводника от температуры

 

Необходимо сказать, что сопротивление электролитов и полупроводников (уголь, селен и другие) с увеличением температуры уменьшается.

Температурная зависимость сопротивления электролита объясняется также в основном изменением удельного сопротивления,однако всегда температурный коэффициент сопротивления — α <0.

 

Поэтому кривая зависимости сопротивленя электролита от температуры имеет вид, представленый на рисунке 2.

 

Рисунок 1. График зависимости удельного сопротивления электролита от температуры

 Ддя полупроводников характер изменения удельного сопротивления от температуры будет схож с таковым для элетролитов.

ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!

Похожие материалы:

Добавить комментарий

от чего зависит сопротивление проводника, формулы для расчета

Одним из физических свойств вещества является способность проводить электрический ток. Электропроводимость (сопротивление проводника) зависит от некоторых факторов: длины электрической цепи, особенностей строения, наличия свободных электронов, температуры, тока, напряжения, материала и площади поперечного сечения.

  • Физический смысл сопротивления
  • Расчет электрической проводимости
  • Зависимость проводимости материала
    • Влияние температуры окружающей среды
    • Деформация и удельное сопротивление
  • Цепи переменного тока
  • Измерение электрической проводимости

Физический смысл сопротивления

Протекание электрического тока через проводник приводит к направленному движению свободных электронов. Наличие свободных электронов зависит от самого вещества и берется из таблицы Д. И. Менделеева , а именно из электронной конфигурации элемента. Электроны начинают ударяться о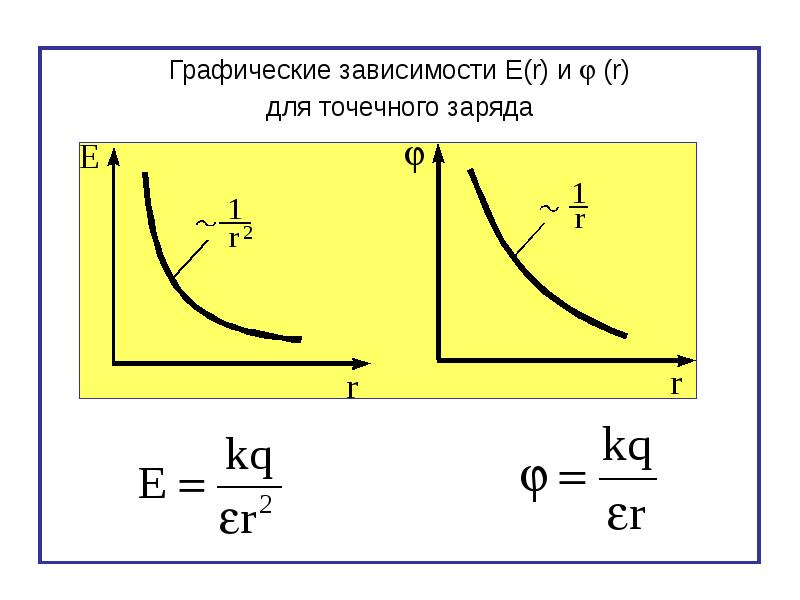

кристаллическую решетку элемента и передают энергию последней. В этом случае возникает тепловой эффект при действии тока на проводник.

При этом взаимодействии они замедляются, но затем под действием электрического поля, которое их ускоряет, начинают двигаться с той же скоростью. Электроны сталкиваются огромное количество раз. Этот процесс и называется сопротивлением проводника.

Следовательно, электрическим сопротивлением проводника считается физическая величина, характеризующая отношение напряжения к силе тока.

Что такое электрическое сопротивление: величина, указывающая на свойство физического тела преобразовывать энергию электрическую в тепловую, благодаря взаимодействию энергии электронов с кристаллической решеткой вещества. По характеру проводимости различаются:

  1. Проводники (способны проводить электрический ток, так как присутствуют свободные электроны).
  2. Полупроводники (могут проводить электрический ток, но при определенных условиях).
  3. Диэлектрики или изоляторы (обладают огромным сопротивлением, отсутствуют свободные электроны, что делает их неспособными проводить ток).

Обозначается эта характеристика буквой R и измеряется в Омах (Ом). Применение этих групп веществ является очень значимым для разработки электрических принципиальных схем приборов.

Для полного понимания зависимости R от чего-либо нужно обратить особое внимание на расчет этой величины.

Расчет электрической проводимости

Для расчета R проводника применяется закон Ома, который гласит: сила тока (I) прямо пропорциональна напряжению (U) и обратно пропорциональна сопротивлению.

Формула нахождения характеристики проводимости материала R (следствие из закона Ома для участка цепи): R = U / I.

Для полного участка цепи эта формула принимает следующий вид: R = (U / I) — Rвн, где Rвн — внутреннее R источника питания.

Зависимость проводимости материала

Способность проводника к пропусканию электрического тока зависит от многих факторов: напряжения, тока, длины, площади поперечного сечения и материала проводника, а также от температуры окружающей среды.

В электротехнике для произведения расчетов и изготовления резисторов учитывается и геометрическая составляющая проводника.

От чего зависит сопротивление: от длины проводника — l, удельного сопротивления — p и от площади сечения (с радиусом r) — S = Пи * r * r.

Формула R проводника: R = p * l / S.

Из формулы видно, от чего зависит удельное сопротивление проводника: R, l, S. Нет необходимости его таким способом рассчитывать, потому что есть способ намного лучше. Удельное сопротивление можно найти в соответствующих справочниках для каждого типа проводника (p — это физическая величина равная R материала длиною в 1 метр и площадью сечения равной 1 м².

Однако этой формулы мало для точного расчета резистора, поэтому используют зависимость от температуры.

Влияние температуры окружающей среды

Доказано, что каждое вещество обладает удельным сопротивлением, зависящим от температуры.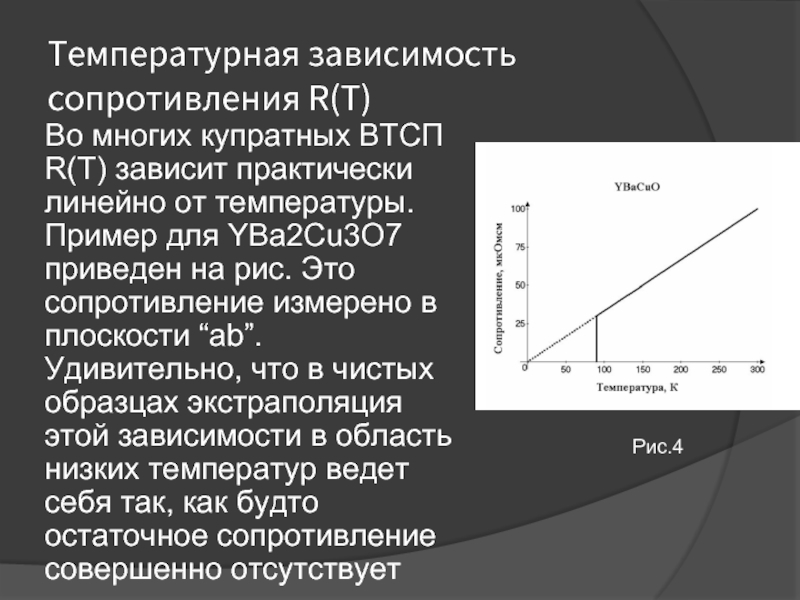

Для демонстрации это можно произвести следующий опыт. Возьмите спираль из нихрома или любого проводника (обозначена на схеме в виде резистора), источник питания и обычный амперметр (его можно заменить на лампу накаливания). Соберите цепь согласно схеме 1.

Схема 1 — Электрическая цепь для проведения опыта

Необходимо запитать потребитель и внимательно следить за показаниями амперметра. Далее следует нагревать R, не отключая, и показания амперметра начнут падать при росте температуры. Прослеживается зависимость по закону Ома для участка цепи: I = U / R. В данном случае внутренним сопротивлением источника питания можно пренебречь: это не отразится на демонстрации зависимости R от температуры. Отсюда следует, что зависимость R от температуры присутствует.

Физический смысл роста значения R обусловлен влиянием температуры на амплитуду колебаний (увеличение) ионов в кристаллической решетке. В результате этого электроны чаще сталкиваются и это вызывает рост R.

Согласно формуле: R = p * l / S, находим показатель, который зависит от температуры (S и l — не зависят от температуры). Остается p проводника. Исходя из это получается формула зависимости от температуры: (R — Ro) / R = a * t, где Ro при температуре 0 градусов по Цельсию, t — температура окружающей среды и a — коэффициент пропорциональности (температурный коэффициент).

Для металлов «a» всегда больше нуля, а для растворов электролитов температурный коэффициент меньше 0.

Формула нахождения p, применяемая при расчетах: p = (1 + a * t) * po, где ро — удельное значение сопротивления, взятое из справочника для конкретного проводника. В этом случае температурный коэффициент можно считать постоянным. Зависимость мощности (P) от R вытекает из формулы мощности: P = U * I = U * U / R = I * I * R. Удельное значение сопротивления еще зависит и от деформаций материала, при котором нарушается кристаллическая решетка.

Деформация и удельное сопротивление

При обработке металла в холодной среде при некотором давлении происходит пластическая деформация. При этом кристаллическая решетка искажается и растет R течения электронов. В этом случае удельное сопротивление также увеличивается. Этот процесс является обратимым и называется рекристаллическим отжигом, благодаря которому часть дефектов уменьшается.

При действии на металл сил растяжения и сжатия последний подвергается деформациям, которые называются упругими. Удельное сопротивление уменьшается при сжатии, так как происходит уменьшение амплитуды тепловых колебаний. Направленным заряженным частицам становится легче двигаться. При растяжении удельное сопротивление увеличивается из-за роста амплитуды тепловых колебаний.

Еще одним фактором, влияющим на проводимость, является вид тока, проходящего по проводнику.

Цепи переменного тока

Сопротивление в сетях с переменным током ведет себя несколько иначе, ведь закон Ома применим только для схем с постоянным напряжением.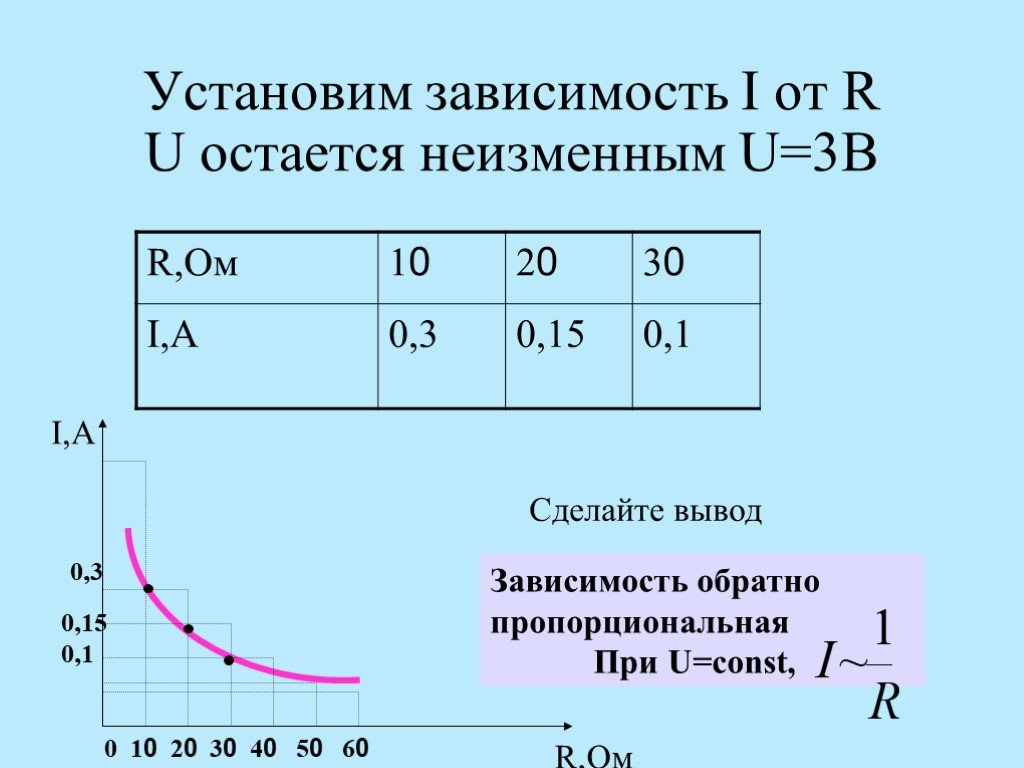

Следовательно, расчеты следует производить иначе.

Полное сопротивление обозначается буквой Z и состоит из алгебраической суммы активного, емкостного и индуктивного сопротивлений.

При подключении активного R в цепь переменного тока под воздействием разницы потенциалов начинает течь ток синусоидального вида. В этом случае формула выглядит: Iм = Uм / R, где Iм и Uм — амплитудные значения силы тока и напряжения. Формула сопротивления принимает следующий вид: Iм = Uм / ((1 + a * t) * po * l / 2 * Пи * r * r).

Емкостное сопротивление (Xc) обусловлено наличием в схемах конденсаторов. Необходимо отметить, что через конденсаторы проходит переменный ток и, следовательно, он выступает в роли проводника с емкостью.

Вычисляется Xc следующим образом: Xc = 1 / (w * C), где w — угловая частота и C — емкость конденсатора или группы конденсаторов. Угловая частота определяется следующим образом:

  1. Измеряется частота переменного тока (как правило, 50 Гц).
  2. Умножается на 6,283.

Индуктивное сопротивление (Xl) — подразумевает наличие индуктивности в схеме (дроссель, реле, контур, трансформатор и так далее). Рассчитывается следующим образом: Xl = wL, где L — индуктивность и w — угловая частота. Для расчета индуктивности необходимо воспользоваться специализированными онлайн-калькуляторами или справочником по физике. Итак, все величины рассчитаны по формулам и остается всего лишь записать Z: Z * Z = R * R + (Xc — Xl) * (Xc — Xl).

Для определения окончательного значения необходимо извлечь квадратный корень из выражения: R * R + (Xc — Xl) * (Xc — Xl). Из формул следует, что частота переменного тока играет большую роль, например, в схеме одного и того же исполнения при повышении частоты увеличивается и ее Z. Необходимо добавить, что в цепях с переменным напряжением Z зависит от таких показателей:

  1. Длины проводника.
  2. Площади сечения — S.
  3. Температуры.
  4. Типа материала.
  5. Емкости.
  6. Индуктивности.
  7. Частоты.

Следовательно и закон Ома для участка цепи имеет совершенно другой вид: I = U / Z. Меняется и закон для полной цепи.

Измерение электрической проводимости

Расчеты сопротивлений требуют определенного количества времени, поэтому для измерений их величин применяются специальные электроизмерительные приборы, которые называются омметрами. Измерительный прибор состоит из стрелочного индикатора, к которому последовательно включен источник питания.

Измеряют R все комбинированные приборы, такие как тестеры и мультиметры. Обособленные приборы для измерения только этой характеристики применяются крайне редко (мегаомметр для проверки изоляции силового кабеля).

Прибор применяется для прозвонки электрических цепей на предмет повреждения и исправности радиодеталей, а также для прозвонки изоляции кабелей.

При измерении R необходимо полностью обесточить участок цепи во избежание выхода прибора из строя. Для это необходимо предпринять следующие меры предосторожности:

  1. Вытянуть вилку из сети.
  2. Включить прибор, при этом произойдет разрядка конденсаторов.
  3. Приступить к измерению или прозвонке.
  4. Установить переключатель в режим измерения сопротивления.
  5. Закоротить щупы прибора, чтобы удостовериться в его работоспособности (покажет очень малое сопротивление).
  6. Измерить необходимый участок.

В дорогих мультиметрах есть функция прозвонки цепи, дублируемая звуковым сигналом, благодаря чему нет необходимости смотреть на табло прибора.

Таким образом, электрическое сопротивление играет важную роль в электротехнике. Оно зависит в постоянных цепях от температуры, силы тока, длины, типа материала и площади поперечного сечения проводника. В цепях переменного тока эта зависимость дополняется такими величинами, как частота, емкость и индуктивность. Благодаря этой зависимости существует возможность изменять характеристики электричества: напряжение и силу тока. Для измерений величины сопротивления применяются омметры, которые используются также и при выявлении неполадок проводки, прозвонки различных цепей и радиодеталей.

Как оценить зависимость между переменными в R

Введение

 

В этой статье я собираюсь продемонстрировать, как оценить зависимость между переменными из наборов данных, чтобы проверить, какие из следующих переменных зависят от других переменных, чтобы ненужные переменные могли быть удалены для создания наиболее подходящей модели в R. Используя комбинацию агрегатной функции с определенными переменными и наборами данных, мы можем выбирать и оценивать зависимости между переменными и оценивать зависимости между переменными из набора данных для создания модели в R. Используя комбинированную функцию, мы можем оценить, как определенное количество изменений в одной переменной может повлиять на другую переменную.

 

Оценка переменных

 

Чтобы оценить зависимости между несколькими переменными вместе, чтобы соответствовать модели, мы можем использовать функцию комбинации вместе с математическими операторами, чтобы оценить зависимости между двумя или более переменными вместе. Например, мы можем использовать оператор двоеточия внутри агрегатной функции, чтобы оценить, сколько переменных зависит друг от друга для создания модели наилучшего соответствия. Чтобы создать модель в R, мы можем использовать различные математические операторы для удаления ненужных переменных.

 

Мы можем определить формулу вместе с арифметическими операторами во многих функциях R. Одной из таких функций является функцияaggregation(), с помощью которой мы можем удалить различные нерелевантные переменные для создания модели.

 

Теперь я продемонстрирую использование функции кластеризации для поиска зависимостей между несколькими переменными вместе. Мы будем использовать набор данных gscars, чтобы продемонстрировать использование агрегатной функции.

  1. > gscars  
  2.                     mg cyl  disp  hp drat    wt  qsec vs bn gr carb  
  3. Mazda RX4           21,0   6 160,0 110 3,90 2,620 16,46  0  1    4    4  
  4. Mazda RX4 Wag       21,0   6 160,0 110 3,90 2,875 17,02  0  1    4    4  
  5. Datsun 710          22,8   4 108,0  93 3,85 2,320 18,61 1  1    4    1 90 026
  6. Шершень 4 Драйв      21,4   6 258,0 110 3,08 3,215 19,44  1  0    3    1  
  7. Hornet Sportabout   18,7   8 360,0 175 3,15 3,440 17,02  0 0    3    2  
  8. Valiant             18,1   6 225,0 105 2,76 3,460 20,22  1  0    3    1  
  9. Дастер 360          14,3   8 360,0 245 3,21 3,570 15,84  0  0    3    4  
  10. Merc 240D           24,4   4 146 . 7  62 3,69 3,190 20,00  1  0    4    2  
  11. Merc 230            22,8   4 140,8  95 3,92 3,150 22,90  1 0 0    4    2  
  12. Мерс 280            19.2 6 167,6 123 3,92 3,440 18,30  1 0    4    4  
  13. Merc 280C           17,8   6 167,6 123 3,92 3,440 18,90  1  0    4    4  
  14. Merc 450SE          16,4   8 275,8 180 3,07 4,070 17,40  0  0    3    3  
  15. Merc 450SL          17,3   8 275,8 180 3,07 3,730 17,60  0  0    3    3  
  16. Merc 450SLC         15,2   8 275 .8 180 3,07 3,780 18,00  0  0    3    3  
  17. Cadillac Fleetwood  10,4   8 472,0 205 2,93 5,250 17,98 0 0    3     4 
  18. Линкольн Континенталь 10.4 8 460,0 215 3,00 5,424 17,82 0 0    3    4  
  19. Chrysler Imperial   14,7   8 440,0 230 3,23 5,345 17,42 0 0 0    3    4  
  20. Fiat 128            32,4   4  78,7  66 4,08 2,200 19,47  1  1    4    1  
  21. Honda Civic         30,4   4 75,7 52 4,93 1,615 18,52 1 1    4    2  
  22. Toyota Corolla      33,9   4 71,1 65 4. 22 1,835 19,90 1  1    4    1  
  23. Toyota Corona      21,5   4 120,1  97 3,70 2,465 20,01 1 0   3    1  
  24. Dod ge Челленджер    15,5 8 318,0 150 2,76 3,520 16,87 0 0    3    2  
  25. AMC Javelin         15,2   8 304,0 150 3,15 3,435 17,30 0 0    3    2  
  26. Camaro Z28          13,3   8 350,0 245 3,73 3,840 15,41  0  0    3    4  
  27. Pontiac Firebird    19.2   8 400.0 175 3.08 3.845 17.05  0  0    3    2  
  28. Fiat X1-9           27.3   4  79.0  66 4.08 1.935 18.90  1  1    4    1  
  29. Porsche 914-2       26.0   4 120.3  91 4.43 2.140 16.70  0  1    5    2  
  30. Lotus Europa        30,4   4 95,1 113 3,77 1,513 16,90 1 1    5    2  
  31. Ford Pantera L      15,8   8 351,0 264 4,22 3,170 14,50  0  1    5    4  
  32. Ferrari Dino        19,7   6 145,0 175 3,62 2,770 15,50  0  1    5    6  
  33. Maserati Bora       15,0   8 301,0 335 3,54 3,570 14,60  0  1    5    8  
  34. Volvo 142E          21,4   4 121,0 10 9 4. 11 2.780 18.60  1  1    4    2  
  35. >  
Мы будем использовать оператор ~ внутри агрегатной функции вместе с оператором двоеточия для найти ассоциативность между несколькими переменными в R. Например, если есть три переменные с именами a, b и c, то a ~ b : c означает, что агрегатная функция создаст модель a после оценки зависимости переменных b и c между каждым другой.

  1. > совокупный (мг ~ гр: миллиард, данные = данные, среднее значение) 
  2.  гр миллиард       мг
  3. 1    4  0 14.10667  
    4. 9002 5 2    5  0 27.05000  
  4. 3    5 1 24.27500  
  5. 4    6 1 22,38000  
В приведенной выше агрегатной функции есть три аргумента. Первый аргумент в формуле указывает, что агрегатная функция представляет мг как функцию модели, вычисляющей среднее значение, а второй аргумент — это переменная, отображающая набор данных. Используя приведенный выше код, агрегатная функция создает модель, в которой модель оценивает зависимость между переменными gr и bn, чтобы проверить зависимость между этими двумя переменными.

  1. > aggregate(mg ~ disp : hp, data = data, mean)  
  2.     disp  hp  mg  
  3. 1   75,7  52 30,4  
  4. 2  146,7  62 24,4  
  5. 3   71,1 65 33,9  
  6. 4   78,7  66 32,4  
  7. 5 79,0 66 27,3
  8. 6 120,3 91 26,0
  9. 7 108,0 93 22,8
  10. 8 140,8 95 22,8
    11. 900 25 9 120,1 97 21,5
  11. 10 225,0 105 18,1
  12. 11 121,0 109 21,4
  13. 12 160,0 110 21,0 9002 6
  14. 13 258,0 110 21,4  
  15. 14 95,1 113 30,4  
  16. 15 167,6 123 18,5  
  17. 16 304,0 150 15,2  
  18. 17 318,0 150 15,5  
  19. 18 145,0 175 19,7  
  20. 19 360,0 175 18,7  
  21. 20 400,0 175 19 .2  
  22. 21 275,8 180 16,3
  23. 22 472,0 205 10,4
  24. 23 460,0 215 10,4
  25. 24 440,0 230 14,7
    26. 90 025 25 350,0 245 13,3  
  26. 26 360,0 245 14,3  
  27. 27 351,0 264 15,8  
  28. 28 301,0 335 15,0  
В приведенной выше агрегатной функции есть три аргумента. Первый аргумент в формуле указывает, что агрегатная функция представляет мг как функцию переменных disp и hp, вычисляющих среднее значение, а второй аргумент является переменной, отображающей набор данных. Используя приведенный выше код, агрегатная функция создает модель, в которой модель оценивает зависимость между переменными disp и hp, чтобы проверить, влияет ли какое-либо изменение в одной переменной на другую переменную или нет, путем сопоставления зависимости между этими двумя переменными.

  1. > совокупный (л.с. ~ мг: цил, данные = данные, среднее) 
  2.     мг цил    л.с.  
  3. 1  21,4   4 109,0  
  4. 2  21,5   4 97,0  
  5. 3 22,8   4 94,0  
  6. 4  24,4   4 62,0  
  7. 5 26,0   4 91,0  
  8. 6 27,3   4 66,0  
  9. 7 30,4   4 82,5  
  10. 8 32,4   4 66,0  
    11. 90 025 9  33,9   4 65,0  
  11. 10 17,8   6 123,0  
  12. 11 18,1   6 105,0  
  13. 12 19,2   6 123,0   900 26
  14. 13 19,7   6 175,0  
  15. 14 21,0   6 110,0  
  16. 15 21,4   6 110,0  
  17. 16 10,4   8 210,0  
  18. 17 13,3   8 245,0  
  19. 18 14,3   8 245,0  
  20. 19 14,7   8 230,0  
  21. 20 15,0   8 335 . 0  
  22. 21 15,2   8 165,0  
  23. 22 15,5   8 150,0  
  24. 23 15,8   8 264,0  
  25. 24 16,4   8 180,0  
    26. 90 025 25 17,3   8 180,0  
  26. 26 18,7   8 175,0  
  27. 27 19,2   8 175,0  
В приведенной выше агрегатной функции есть три аргумента. Первый аргумент в формуле указывает, что агрегатная функция представляет hp как функцию переменных mg и cyl, вычисляющих среднее значение, а второй аргумент является переменной, отображающей набор данных. Используя приведенный выше код, агрегатная функция создает модель, в которой модель оценивает зависимость между переменными mg и cyl, чтобы проверить, влияет ли какое-либо изменение в одной переменной на другую переменную или нет, путем сопоставления зависимости между этими двумя переменными.

  1. > aggregate(wt ~ gr : qsec, data = data, mean)  
  2.    gr  qsec     wt  
  3. 1     5 14,50 3,1700  
    4. 9 0025 2     5 14,60 3,5700  
  4. 3     3 15,41 3,8400  
  5. 4     5 15,50 2,7700  
  6. 5 3 15,84 3,5700  
  7. 6     4 16,46 2,6200  
  8. 7     5 16,70 2,1400  
  9. 8     3 16,87 3,5200  
  10. 9     5 16,90 1,5130  
  11. 10    3 17,02 3,4400  
  12. 11    4 17,02 2,8750  
  13. 12    3 17,05 3,8450  
  14. 13    3 17,30 3,4350  
  15. 14    3 17,40 4,0700  
  16. 15    3 17,42 5,3450  
  17. 16    3 17,60 3,7300  
  18. 17    3 17,82 5,4240  
  19. 18    3 17,98 5,2500  
  20. 19    3 18,00 3,7800  
  21. 20    4 18,30 3,4400  
  22. 21    4 18,52 1,6150  
  23. 22    4 18,60 2,7800  
  24. 23    4 18,61 2. 3200  
  25. 24    4 18,90 2,6875  
  26. 25    3 19,44 3,2150  
  27. 26    4 19.47 2.2000  
  28. 27    4 19.90 1.8350  
  29. 28    4 20.00 3.1900  
  30. 29    3 20,01 2,4650  
  31. 30    3 20,22 3,4600  
  32. 31    4 22,90 3,1500  

В приведенной выше агрегатной функции есть три аргумента. Первый аргумент в формуле указывает, что агрегатная функция представляет вес как функцию переменных gr и qsec, вычисляющую среднее значение, а второй аргумент является переменной, отображающей набор данных. Используя приведенный выше код, агрегатная функция создает модель, в которой модель оценивает зависимость между переменными gr и qsec, чтобы проверить, влияет ли какое-либо изменение в одной переменной на другую переменную или нет, путем сопоставления зависимости между этими двумя переменными.

 

Сводка

 

В этой статье я продемонстрировал, как оценить взаимодействие между переменными из наборов данных, чтобы проверить, какая из следующих переменных зависит от других переменных, чтобы можно было удалить ненужные переменные для создания модели, наиболее подходящей в R. . 

Зависимость и корреляция | Р-блогеры

[Эта статья была впервые опубликована на mickeymousemodels и любезно предоставлена ​​R-блогерами]. (Вы можете сообщить о проблеме с содержанием на этой странице здесь)

Хотите поделиться своим контентом с R-блогерами? нажмите здесь, если у вас есть блог, или здесь, если у вас его нет.

В повседневной жизни я гораздо чаще слышу слово «корреляция», чем «зависимость». Какая разница? Корреляция в ее наиболее распространенной форме является мерой линейной зависимости; подвох в том, что не все зависимости линейны. Набор коррелированных случайных величин полностью находится внутри большего набора зависимых случайных величин; корреляция подразумевает зависимость, но не наоборот. Вот несколько глупых (но, надеюсь, интересных) примеров, иллюстрирующих это утверждение:

 н <- 5000
df <- data.frame(x=rnorm(n), y=rnorm(n, среднее=5, sd=2))
plot(df, xlim=c(-6, 6), ylim=c(-2, 12), main="Улей")
mtext("X и Y независимы (и, следовательно, не коррелированы)")
savePlot("улей.
 
 png") 

 n <- 2500
df <- data.frame(x=rexp(n), y=rexp(n, rate=2))
plot(df, xlim=c(-0,05, 10), ylim=c(-0,05, 5), main="Бомбардировщик B-2")
mtext("X и Y независимы (и, следовательно, не коррелированы)")
savePlot("bomber.png") 

 n <- 5000
df <- data.frame(x=runif(10000))
df$y <- runif(10000, -abs(0,5 - df$x), abs(0,5 - df$x))
plot(df, xlim=c(-0,05, 1,05), ylim=c(-0,55, 0,55), main="Галстук-бабочка/бабочка")
mtext("X и Y зависимы, но не коррелированы")
savePlot("бабочка.png") 92 <= 0,25)
сюжет (df, main = "Сатурн")
mtext("X и Y зависимы, но не коррелированы")
savePlot("saturn.png") 

 n <- 5000
df <- data.frame(x=rnorm(n))
df$y <- с (df, x * (2 * as.integer (abs (x) > 1,54) - 1))
plot(df, xlim=c(-4, 4), ylim=c(-4, 4), main="Разводной мост")
mtext("X и Y зависимы, но не коррелированы")
savePlot("bridge.png") 

 n <- 1000
df <- data.frame(x=rnorm(n), z=sample(c(-1, 1), size=n, replace=TRUE))
df$y <- с (df, z * x)
df <- df[ c("x", "y")]
plot(df, xlim=c(-4, 4), ylim=c(-4, 4), main="Карта сокровищ")
mtext("X и Y зависимы, но не коррелированы")
savePlot("сокровище. png")

Последние два являются классическими примерами: X и Y нормально распределены, но (X, Y) не является двумерной нормой.

Я признаю, что две экспоненты немного нелогичны для меня, по крайней мере визуально. (Они на втором графике сверху, который отдаленно напоминает B-2.) Переменные независимы; если вы регрессируете Y на X, вы получите плоскую линию. Тем не менее, каким-то образом, если бы я посмотрел на этот график, не зная, как генерируются переменные, я бы хотел провести диагональную линию, указывающую вверх и вправо. Во всяком случае, это показывает, что мне, вероятно, не следует проводить регрессии «путем проверки».

К оставьте комментарий для автора, перейдите по ссылке и оставьте комментарий в их блоге: mickeymousemodels .

R-bloggers.com предлагает ежедневных обновлений по электронной почте новостей R и руководств по изучению R и многим другим темам. Нажмите здесь, если вы хотите опубликовать или найти работу R/data-science.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *

*