Инженерная помощь расчет площади воздуховодов и фасонных: Расчет площади воздуховодов и фасонных изделий

Расчет местных сопротивлений в системах вентиляции | C.O.K. archive | 2012

Рис. 1. Зависимость КМС унифицированных приточных тройников от величины

Такие потери пропорциональны динамическому давлению pд = ρv2/2, где ρ — плотность воздуха, равная примерно 1,2 кг/м3 при температуре около +20 °C, а v — его скорость [м/с], как правило, за сопротивлением. Коэффициенты пропорциональности ζ, называемые коэффициентами местного сопротивления (КМС), для различных элементов систем В и КВ обычно определяются по таблицам, имеющимся, в частности, в [2] и в ряде других источников.

Наибольшую сложность при этом чаще всего вызывает поиск КМС для тройников или узлов ответвлений, поскольку в этом случае необходимо принимать во внимание вид тройника (на проход или на ответвление) и режим движения воздуха (нагнетание или всасывание), а также отношение расхода воздуха в ответвлении к расходу в стволе Lo ʹ = Lo/Lc и площади сечения прохода к площади сечения ствола fn ʹ = fn/fc.

Для тройников при всасывании нужно учитывать еще и отношение площади сечения ответвления к площади сечения ствола fo ʹ = fo/fc.

В руководстве [2] соответствующие данные приведены в табл. 22.36–22.40. Однако, при больших относительных расходах в ответвлении КМС меняются весьма резко, поэтому в этой области рассматриваемые таблицы вручную интерполируются с трудом и со значительной погрешностью.

Кроме того, в случае использования электронных таблиц MS Excel опять-таки желательно иметь формулы для непосредственного вычисления КМС через отношения расходов и сечений. При этом такие формулы должны быть, с одной стороны, достаточно простыми и удобными для массового проектирования и использования в учебном процессе, но, в то же время, не должны давать погрешность, превышающую обычную точность инженерного расчета.

Ранее подобная задача была решена автором применительно к сопротивлениям, встречающимся в водяных системах отопления [3]. Рассмотрим теперь данный вопрос для механических систем В и КВ. Ниже приведены результаты аппроксимации данных [2] для унифицированных тройников (узлов ответвлений) на проход. Общий вид зависимостей выбирался, исходя из физических соображений с учетом удобства пользования полученными выражениями при обеспечении допустимого отклонения от табличных данных:

• для приточных тройников, при Lo ʹ ≤ 0,7 и fn ʹ ≥ 0,5:
  
  а при Lo ʹ ≤ 0,4 можно пользоваться упрощенной формулой:
  
• для вытяжных тройников:
  
   

Нетрудно заметить, что относительная площадь прохода fn ʹ при нагнетании или соответственно ответвления fo ʹ при всасывании влияет на КМС одинаковым образом, а именно с увеличением fn ʹ или fo ʹ сопротивление будет уменьшаться, причем числовой коэффициент при указанных параметрах во всех приведенных формулах один и тот же, а именно (–0,25).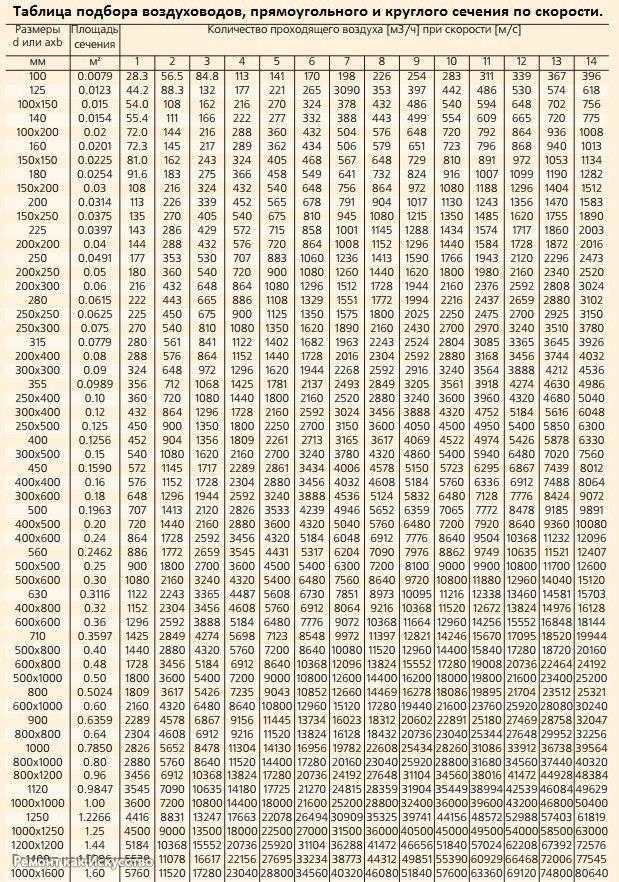 Кроме того, и для приточных, и для вытяжных тройников при изменении расхода воздуха в ответвлении относительный минимум КМС имеет место при одинаковом уровне Lo ʹ = 0,2.

Данные обстоятельства говорят о том, что полученные выражения, несмотря на свою простоту, в достаточной мере отражают общие физические закономерности, лежащие в основе влияния исследуемых параметров на потери давления в тройниках любого типа. В частности, чем больше fn ʹ или fo ʹ, т.е. чем ближе они к единице, тем меньше меняется структура потока при прохождении сопротивления, а значит, и меньше КМС.

Для величины Lo ʹ зависимость является более сложной, но и здесь она будет общей обоих режимов движения воздуха. Представление о степени соответствия найденных соотношений и исходных значений КМС дает рис. 1, где показаны результаты обработки таблицы 22.37 для КМС унифицированных тройников (узлов ответвлений) на проход круглого и прямоугольного сечения при нагнетании. Примерно такая же картина получается и для аппроксимации табл.

22.38 с помощью формулы (3).

Заметим, что, хотя в последнем случае речь идет о круглом сечении, нетрудно убедиться, что выражение (3) достаточно удачно описывает и данные табл. 22.39, относящиеся уже к прямоугольным узлам. Погрешность формул для КМС в основном составляет 5–10 % (максимально до 15 %). Несколько более высокие отклонения может давать выражение (3) для тройников при всасывании, но и здесь это можно считать удовлетворительным с учетом сложности изменения сопротивления в таких элементах.

Во всяком случае, характер зависимости КМС от влияющих на него факторов здесь отражается очень хорошо. При этом полученные соотношения не требуют никаких иных исходных данных, кроме уже имеющихся в таблице аэродинамического расчета. В самом деле, в ней в явном виде должны быть указаны и расходы воздуха, и сечения на текущем и на соседнем участке, входящие в перечисленные формулы. Особенно это упрощает вычисления при использовании электронных таблиц MS Excel.

В то же время формулы, приведенные в настоящей работе, весьма просты, наглядны и легко доступны для инженерных расчетов, особенно в MS Excel, а также в учебном процессе. Их применение позволяет отказаться от интерполяции таблиц при сохранении точности, требуемой для инженерных расчетов, и непосредственно вычислять КМС тройников на проход при самых разнообразных соотношениях сечений и расходов воздуха в стволе и ответвлениях.

Этого вполне достаточно для проектирования систем В и КВ в большинстве жилых и общественных зданий.

Новости сетевых электронных изданий открытого доступа

Актуальные проблемы комплексной безопасности в строительстве, тенденции развития в современных условиях : сборник докладов Всероссийской научно-практической конференции (г. Москва, 30 ноября 2022 г.)

20.02.2023

Аннотация: Актуальные проблемы комплексной безопасности в строительстве, тенденции развития в современных условиях [Электронный ресурс] : сборник докладов Всероссийской научно-практической конференции (г. Москва, 30 ноября 2022 г.) / Министерство науки и высшего образования Российской Федерации, Национальный исследовательский Московский государственный строительный университет, институт гидроэнергетического строительства, кафедра комплексной безопасности в строительстве.

— Электрон. дан. и прогр. (2 Мб). — Москва : Издательство МИСИ – МГСУ, 2023. — URL: https://mgsu.ru/resources/izdatelskaya-deyatelnost/izdaniya/izdaniya-otkr-dostupa/. — Загл.с титул. экрана. ISBN 978-5-7264-3206-9 Подробнее →

Актуальные проблемы строительной отрасли и образования – 2022 : сборник докладов Третьей Национальной научной конференции (г. Москва, 19 декабря 2022 г.)

08.02.2023

Актуальные проблемы строительной отрасли и образования – 2022 [Электронный ресурс] : сборник докладов Третьей Национальной научной конференции (г. Москва, 19 декабря 2022 г.) / Министерство науки и высшего образования Российской Федерации, Национальный исследовательский Московский государственный строительный университет, управление научной политики. — Электрон. дан. и прогр. (58 Мб) — Москва: Издательство МИСИ – МГСУ, 2023. — Режим доступа: https://mgsu.ru/resources/izdatelskaya-deyatelnost/izdaniya/izdaniya-otkr-dostupa/. — Загл. с титул.

экрана. 

ISBN 978-5-7264-3202-1 

Подробнее →

Современные проблемы и решения в системах отопления, вентиляции и теплоснабжения : сборник материалов IX Всероссийской научно-практической конференции, посвящённой 130-летию со дня рождения профессора П.Н. Каменева (г. Москва, 17–18 ноября 2022 г.)

14.12.2022

Современные проблемы и решения в системах отопления, вентиляции и теплоснабжения [Электронный ресурс] : сборник материалов IX Всероссийской научно-практической конференции, посвящённой 130-летию со дня рождения профессора П.Н. Каменева (г. Москва, 17–18 ноября 2022 г.) / Министерство науки и высшего образования Российской Федерации, Национальный исследовательский Московский государственный строительный университет, институт инженерно-экологического строительства и механизации. — Электрон. дан. и прогр. (5,5 Мб). — Москва : Издательство МИСИ – МГСУ, 2022. — URL: https://mgsu.

ru/resources/izdatelskaya-deyatelnost/izdaniya/izdaniya-otkr-dostupa/.— Загл. с титул. экрана. 

ISBN 978-5-7264-3155-0 

Подробнее →

Геоэкологические проблемы техногенного этапа истории Земли — 2022 [Электронный ресурс] : сборник материалов Всероссийской (национальной) научно-практической конференции (г. Москва, 14 октября 2022 г.)

14.12.2022

Геоэкологические проблемы техногенного этапа истории Земли — 2022 [Электронный ресурс] : сборник материалов Всероссийской (национальной) научно-практической конференции (г. Москва, 14 октября 2022 г.) / Министерство науки и высшего образования Российской Федерации, Национальный исследовательский Московский государственный строительный университет, институт гидротехнического и энергетического строительства, кафедра инженерных изысканий и геоэкологии. — Электрон. дан. и прогр. (6 Мб). — Москва : Издательство МИСИ – МГСУ, 2022. — URL: https://mgsu.

ru/resources/izdatelskaya-deyatelnost/izdaniya/izdaniya-otkr-dostupa/ — Загл. с титул. экрана.

ISBN 978-5-7264-3158-1 

Подробнее →

Современные проблемы гидравлики и гидротехнического строительства : сборник тезисов докладов V Всероссийского научно-практического семинара (г. Москва, 25 мая 2022 г.)

04.10.2022

Современные проблемы гидравлики и гидротехнического строительства [Электронный ресурс] : сборник тезисов докладов V Всероссийского научно-практического семинара (г. Москва, 25 мая 2022 г.) / Министерство науки и высшего образования Российской Федерации, Национальный исследовательский Московский государственный строительный университет, кафедра гидравлики и гидротехнического строительства. — Электрон. дан. и прогр. (2 Мб). – Москва : Издательство МИСИ – МГСУ, 2022. – Режим доступа: http://mgsu.ru/resources/izdatelskaya-deyatelnost/izdaniya/izdaniya-otkr-dostupa/ — Загл. с титул. экрана.

ISBN 978-5-7264-3111-6

Подробнее →

УСТОЙЧИВОЕ РАЗВИТИЕ ТЕРРИТОРИЙ

22. 09.2022

 Устойчивое развитие территорий [Электронный ресурс] : сборник докладов IV  Международной  научно-практической  конференции  (г.  Москва,  30–31  мая 2022  г.)  /  Министерство  науки  и  высшего  образования  Российской  Федерации, Национальный  исследовательский  Московский  государственный  строительный университет, институт строительства и архитектуры. — Электрон. дан. и прогр. 

(26,5  Мб).  —  Москва:  Издательство  МИСИ  –  МГСУ,  2022.  —  

URL: http://mgsu.ru/resources/izdatelskaya-deyatelnost/izdaniya/izdaniya-otkr-dostupa/2022/sbornik URT.pdf. —Загл. с титул. экрана. 

ISBN 978-5-7264-3104-8

Подробнее →

Зелёные технологии в жизненном цикле зданий и сооружений [Электронный ресурс] : сборник материалов Всероссийской конференции (г. Москва, 25 мая 2022 г.)

11.07.2022

Зелёные технологии в жизненном цикле зданий и сооружений [Электронный ресурс] : сборник материалов Всероссийской конференции (г.

Москва, 25 мая 2022 г.) / Министерство науки и высшего образования Российской Федерации, Национальный исследовательский Московский государственный строительный университет, институт инженерно- экологического строительства и механизации. — Электрон. дан. и прогр. (5,5 Мб). — Москва : Издательство МИСИ – МГСУ, 2022. — URL: http://mgsu.ru/resources/izdatelskaya-deyatelnost/izdaniya/izdaniya-otkr-dostupa/. — Загл. с титул. экрана. 

ISBN 978-5-7264-3069-0 

Подробнее →

Тенденции развития физической культуры и спорта в современных условиях [Электронный ресурс] : сборник докладов XV Международной научно-практической конференции (г. Москва, 9–10 июня 2022 г.)

04.07.2022

Тенденции развития физической культуры и спорта в современных условиях [Электронный ресурс] : сборник докладов XV Международной научно-практической конференции (г. Москва, 9–10 июня 2022 г.) / ред. кол.: проф. В.А. Никишкин, канд. биол. наук, доцент Н.Н. Бумарскова, канд. социол. наук, проф. С.И. Крамской ; Министерство науки и высшего образования Российской Федерации, Национальный исследовательский Московский государственный строительный университет, институт физической культуры и спорта. — Электрон. дан. и прогр. (5,5 Мб). — Москва : Издательство МИСИ – МГСУ, 2022. — URL: https://mgsu.ru/resources/izdatelskaya-deyatelnost/izdaniya/izdaniya-otkr-dostupa/ — Загл. с титул. экрана. 

ISBN 978-5-7264-3060-7 

Подробнее →

Оптимальная форма поперечного сечения газо/воздуховодов

Всемирный инженерно-технический журнал Vol.04 No.03 (2016), ID статьи:72372,6 страниц
10.4236/wjet.2016.43D030

Оптимальная форма поперечного сечения газо/воздуховодов

Yongjian Gu

Департамент морской инженерии США Академия торгового флота США Кингс-Пойнт, Нью-Йорк, США

Поступила в редакцию: 24 сентября 2016 г. ; Принято: 22 октября 2016 г.; Опубликовано: 29 октября 2016 г.

АННОТАЦИЯ

На промышленных предприятиях, кораблях и в зданиях большое количество газо- и воздуховодов применяется для соединения оборудования, ОВКВ, среднего транспорта, выхлопа и т. д. Эти воздуховоды могут быть спроектированы в различной формы поперечного сечения, например, круглой или прямоугольной. Путем геометрического расчета формы поперечного сечения воздуховода и инженерного опыта автор показывает, что круглое поперечное сечение является оптимальной формой в системе воздуховодов. Круглый воздуховод имеет более короткий периметр, чем воздуховоды другой формы поперечного сечения, и более прочную конструкцию в тех же рабочих условиях. Количественно определена экономия материала круглого воздуховода за счет меньшего периметра. В статье показано, что круглый воздуховод экономически привлекателен. Экономический анализ экономии материальных затрат проиллюстрирован примером. Для системы длинных воздуховодов экономия материалов и затрат на них значительна.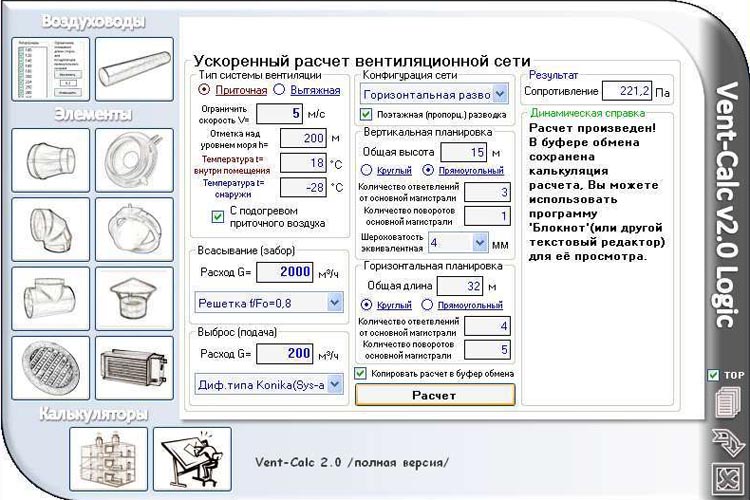 Предполагается, что круглый воздуховод в системе газо- и воздуховодов должен иметь приоритет, пока позволяют полевые условия. В документе экономия материальных затрат также преобразуется в PW, AW и FW, используемые для экономического анализа LCC.

Ключевые слова:

Оптимальные, Воздуховоды, Форма поперечного сечения, Экономический и стоимостной анализ подключение оборудования и средний транспорт, например, в HVAC и выхлопных системах. Формы поперечного сечения воздуховодов часто проектируются и изготавливаются прямоугольными, квадратными или круглыми. Материал воздуховода чаще всего представляет собой оцинкованный металлический лист. В зависимости от целей применения воздуховода используются изоляционные материалы. С геометрической точки зрения круглый воздуховод имеет наименьший периметр по сравнению с прямоугольным и квадратным воздуховодами с одинаковой площадью проходного сечения. Следовательно, материал круглого воздуховода по сравнению с квадратным или прямоугольным воздуховодом с равной площадью поперечного сечения может быть уменьшен. В то время как при равных периметрах круглый воздуховод имеет наибольшую площадь проходного сечения, что, по-видимому, уменьшит трение потока. Тем не менее, круглый воздуховод должен быть оптимальной конструкцией для воздуховодов. Соотношения периметра и площади поперечного сечения этих воздуховодов показаны в Таблице 1. Если система воздуховодов имеет длину в тысячи футов, экономия материала и экономия затрат на материалы будут значительными, и другие преимущества могут быть получены при использовании круглого воздуховода.

2. Экономия материала и преимущества использования круглого воздуховода

При проектировании системы воздуховодов форма поперечного сечения воздуховода может быть круглой или прямоугольной с одинаковым трением потока, что означает одинаковую площадь поперечного сечения потока. Уравнение, связывающее диаметр D круглого воздуховода и длины сторон прямоугольного воздуховода, будет [1]

(1)

Тогда k, отношение периметра круглого воздуховода к прямоугольному воздуховоду, равно 9. 0006

(3)

Уравнение (3) становится после преобразования

(4)

где R = a/b = длина длинной стороны/длина короткой стороны , Результаты соотношения периметров k варьируются в зависимости от соотношения сторон Rand. Описание приведено в таблице 2.

Можно видеть, что для круглого воздуховода требуется меньший периметр по сравнению с прямоугольным воздуховодом. Чем больше R, тем меньше k, что означает меньше материала для круглого воздуховода, чем для прямоугольного. Из практики промышленности значение R обычно равно 9.0006

Таблица 1. Отношения периметра и площади.

Таблица 2. Отклонение K от R.

около 2. Таким образом, материал воздуховода можно сэкономить на 20%, используя круглый воздуховод. Другими словами, экономия затрат на материал для круглого воздуховода составляет 20% по сравнению с прямоугольным воздуховодом.

1) Экономия затрат на листовой металл

Оцинкованная металлическая сталь является наиболее распространенным материалом, используемым при изготовлении воздуховодов. Стоимость изготовления воздуховодов обычно зависит от общей массы воздуховода и фитингов. Для прямого воздуховода из оцинкованной металлической стали цена за единицу калибров 26, 24, 22, 20 и 18 менее 454 кг (1000 фунтов) составляет около 5,79 долларов США./ кг (2,63 доллара США за фунт) [2]. В Таблице 3 показана экономия затрат на материал на единицу длины воздуховода 813 мм x 406 мм (32″ × 16″) при R = 2. будет происходить всякий раз, когда на поверхности объекта есть прерывность или неоднородность. Периметр прямоугольного воздуховода имеет резкие повороты, а периметр круглого воздуховода продолжается плавно. Таким образом, круглый воздуховод с меньшей концентрацией напряжений будет иметь более длительный срок эксплуатации.

Стабильность конструкции

Также известно, что когда в воздуховоде течет поток сжатого воздуха или газа, воздуховод будет обозначать внутреннюю силу. Круглый воздуховод имеет более высокую устойчивость конструкции, чем прямоугольный воздуховод, согласно анализу внутренних напряжений.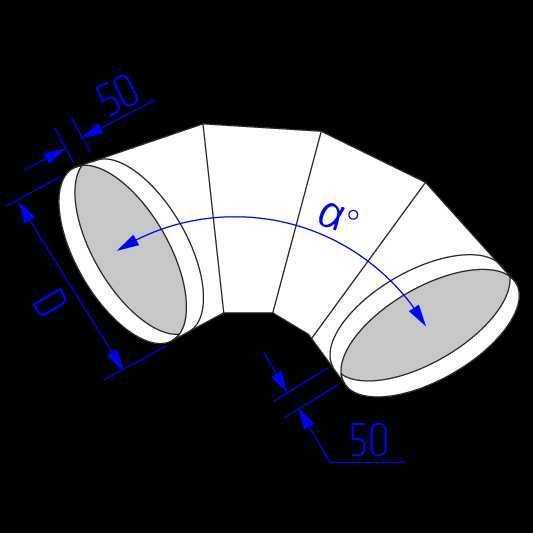 Таким образом, в круглом воздуховоде могут не потребоваться прочностные компоненты, используемые в прямоугольном воздуховоде, например стальные элементы со стороны сечения и направления потока. Это уменьшит материал воздуховода и трудозатраты на изготовление. В результате снижается стоимость материалов и изготовления.

3) Прочая экономия

Если требуется изоляция, воздуховоды обычно облицовываются лицевым стекловолоконным покрытием (внутренняя облицовка воздуховода) или обертываются снаружи многослойным стекловолоконным полотном размером 25 мм на 50 мм (1 дюйм на 2 дюйма) (обертка воздуховода). ). Поскольку периметр круглого воздуховода меньше периметра прямоугольного воздуховода, количество изоляционных материалов будет меньше.

Таблица 3. Экономия затрат на материал на единицу длины.

Стоимость доставки зависит от массы материала, которая обычно составляет около 0,33 долл. США/кг (0,15 долл. США/фунт) [2]. Поскольку масса воздуховода снижается из-за уменьшения материала воздуховода, соответственно снижается стоимость доставки.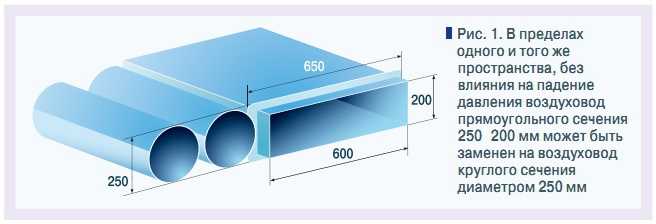

Пример:

Система воздуховодов длиной 305 м (1000 футов) будет подавать 102 м ³ воздуха в минуту (3600 CFM). При расчете трение на 305 м (100 футов) воздуховода составляет 2 мм (0,08 дюйма водяного столба), а диаметр круглого воздуховода D = 610 мм (24 дюйма) выбран [3]. При равном трении в качестве альтернативы можно использовать прямоугольный воздуховод размером 813 мм × 406 мм (32 дюйма × 16 дюймов). Следовательно,

Периметр круглого воздуховода равен

L = πD = 1,92 м (6,3 фута)

Периметр прямоугольного воздуховода будет равен

L = 813 мм × 406 мм (32″ × 16″) = 2,4 м (8,0 футов)

Для системы воздуховодов 22 калибра длиной 305 м (1000 футов) общая экономия материала воздуховода составит

Экономия материала на единицу квадратной площади = 305 м × (2,4 м − 1,92 м) = 146,4 м = 305 м × 19,42 $/м = 5923 $

В таблице 4 показана экономия затрат на материалы для системы воздуховодов длиной 305 м (1000 футов) с калибром 26, 24, 22, 20 и 18 при одинаковых проектных условиях соответственно. . Можно увидеть, что для длинной системы воздуховодов экономия на материальных затратах значительна!

3. Экономия затрат на материалы в анализе LCC

Экономия затрат на материалы может применяться вместе с другим анализом экономии в стоимости жизненного цикла (LCC), чтобы получить общую экономию затрат на систему воздуховодов в течение заданного времени подъема системы. Другая экономия, например, затраты на эксплуатацию и техническое обслуживание и ремонт или стоимость MV. Экономия материальных затрат должна быть преобразована в PW, AW и FW в анализе LCC [4]. PW, AW и FW экономии материальных затрат рассчитываются по

(5)

(6)

(7)

В качестве иллюстрации в таблице 5 показаны PW, AW и FW экономии материальных затрат калибра 22 из приведенного выше примера в разделе 2 со следующими назначениями.

Таблица 4. Материал Экономия затрат.

Таблица 5. Экономия при изменении i и n.

Процентная ставка (i) = 6%, 8% и 10% соответственно

Срок службы (n) = 15, 20, 25 и 30 лет соответственно

4. Заключение

Форма поперечного сечения системы газо- и воздуховодов, применяемых для подключения оборудования, ОВиК, среднего транспорта и вытяжки, можно выбрать как круглую, так и прямоугольную. Однако из геометрических расчетов и анализа напряжений следует, что круглый воздуховод имеет меньший периметр и более прочную структуру потока. В результате материал воздуховода может быть сохранен при одинаковом трении потока и других преимуществах, таких как срок службы воздуховода, который может быть получен в тех же рабочих условиях при использовании круглого воздуховода по сравнению с прямоугольным воздуховодом. Расчет из примера показывает, что для большой системы воздуховодов экономия материалов и затрат на материалы значительна.

Сделан вывод, что круглая форма поперечного сечения оптимальна по сравнению с квадратной и прямоугольной формой для газовоздушной системы.

Рекомендуется использовать круглый воздуховод в газо- и воздуховодах, если позволяют полевые условия.

Процитировать эту статью

Gu, YJ (2016) Оптимальная форма поперечного сечения газоходов/воздуховодов. Всемирный журнал инженерии и технологий, 4, 250-255. http://dx.doi.org/10.4236/wjet.2016.43D030

Ссылки

1. 1. Линдебург, М. Р. (2006) Справочное руководство по машиностроению, Professional Publications, Inc., 12-е издание, Belmont, Chap. 20, 20-14.


2. 2. Томпсон, Дж.А. (2014) Национальный оценщик сантехники и ОВКВ. Книжная компания Craftsman, Нью-Йорк.


3. 3. (2015) Бюро испытаний, настройки и балансировки (TABB). www.tabbcertificate.org


4. 4. Салливан, В. (2012) Инженерная экономика, Пятнадцатое издание, Prentice Hall. www.pearsonhighered.com

Сокращения

AW: годовая стоимость

CFM: кубический фут в минуту

D: диаметр круглого воздуховода

FW: будущая стоимость

HVAC: отопление, вентиляция и кондиционирование воздуха по периметру

6 Lduct

2 поперечное сечение

LCC: стоимость жизненного цикла

MV: рыночная стоимость

PW: текущая стоимость

R: соотношение сторон

a: длина короткой стороны прямоугольного воздуховода

b: длина длинной стороны прямоугольного воздуховода

футов: фут, фута

I: Годовая процентная ставка

K: соотношение периметра

фунт: фунт

N: период срока службы

$: доллар США

. отправить следующую рукопись в SCIRP, и мы предоставим вам лучший сервис:

Прием предварительных запросов по электронной почте, Facebook, LinkedIn, Twitter и т. д.

Широкий выбор журналов (включая 9 тем, более 200 журналов)

Предоставление 24-часового высококачественного обслуживания

Удобная онлайн-система подачи заявок

Справедливая и быстрая система рецензирования

Эффективная процедура набора текста и корректуры

Отображение результатов загрузок и посещений, а также количества цитируемых статей

Максимальное распространение вашей исследовательской работы

Отправьте рукопись по адресу: http://papersubmission.scirp.org/

Или свяжитесь с [email protected]

Air Balance: Как исправить горячие и холодные точки в Главная

Вы все это видели. У вас, вероятно, есть один. Загроможденная неиспользуемая комната для гостей дальше по коридору. Коробки с елочными украшениями забиты в шкафу, маминые корзины для рукоделия свалены в угол. Вы говорите себе, что из этой комнаты получится отличный офис, но в ней чертовски холодно. Не позволяйте этому пропадать зря. Вы можете возместить стоимость неиспользованного номера авиабалансом.

Вот в чем дело: холодные места доставляют неудобства вам и вашей семье, лишая вас площади, за которую вы заплатили своим тяжелым трудом. Но не отчаивайтесь, балансировка воздуха в вашей системе HVAC может это исправить. Балансировка воздуха требует тестирования, инженерных расчетов, регулировки и часто модификации или ремонта воздуховодов, так что это не простая прогулка по парку для вашего среднего подрядчика HVAC. На самом деле, большинство подрядчиков по ОВКВ даже не предлагают баланс воздуха. Чтобы правильно выполнить работу, нужен хороший квалифицированный подрядчик по ОВК, такой как команда SuperTech HVAC.

И хотя задача может показаться сложной, балансировка воздуха поможет вам во всех отношениях. В этой статье мы расскажем все, что вам нужно знать о воздушном балансе (чтобы вы могли лучше спать по ночам).

Воздух в ваших комнатах неровный? Позвоните нам сейчас, чтобы сбалансировать его!

Что такое балансировка воздуха?

Как следует из названия, балансировка воздуха относится к процессу оптимизации воздушного потока через вашу систему HVAC для поддержания желаемой температуры равномерно по всему дому.

 

Когда вам нужна балансировка системы ОВКВ?

У вас нестабильный нагрев и охлаждение

Хотите верьте, хотите нет, но несбалансированный воздух в вашей системе HVAC является причиной номер один, из-за которой вы испытываете несоответствие температуры в вашем доме. Хороший дизайн и монтаж воздуховодов, среди прочего, являются лучшим способом предотвращения дисбаланса воздуха. И если в одной комнате аномально холодно и жарко, проблема, скорее всего, распространится по всему дому, только менее очевидна.

Это неприглядная правда о воздуховодах – плохая практика проектирования и монтажа воздуховодов появилась в жилом секторе с 1970-х годов, когда господствовало массовое производство быстрых и дешевых. Чтобы узнать больше о воздуховодах, см. наши блоги о воздуховодах.

Вот совок: при борьбе с горячими и холодными точками быстрое решение — включить отопление или кондиционер. Не. Это приведет к более серьезным проблемам, таким как преждевременная смерть вашего блока HVAC и заоблачные счета за электроэнергию.

У вас слишком маленькие обратные клапаны

Обратите внимание: приточные и возвратные вентиляционные отверстия подобны артериям и венам внутри вашего тела, они подают свежий воздух в ваши комнаты и возвращают использованный воздух обратно в систему HVAC. Ваша система HVAC должна иметь правильное количество приточных и возвратных вентиляционных отверстий для регулирования впуска и выпуска воздуха.

Не буду вам врать, такое случается редко, так как строители часто предпочитают устанавливать один большой центральный возврат, чтобы сэкономить на затратах. Этот опрометчивый путь в конечном итоге будет стоить вам тысячи излишков платы за электроэнергию в год.

Теперь, для ясности, один центральный возврат работает, если двери в вашем доме постоянно открыты. Но закрывайте двери спальни на ночь, и вы будете голодать в возвращении и создадите среду отрицательного давления, которая всасывает наружный воздух через маленькие щели и щели. Нефильтрованный воздух может нести аллергены и другие нежелательные частицы, портя общее качество воздуха при дерегулировании температуры. Это заставляет ваш блок HVAC работать в два раза дольше, что означает более высокие счета.

Вы можете подумать, что моя система HVAC нуждается в балансировке воздуха. Но как? Вот тут-то и приходят на помощь настоящие специалисты по HVAC. Если вы попытаетесь выполнить следующие действия без помощи обученного специалиста, вы принесете больше вреда, чем пользы.

Как сбалансировать систему воздушного отопления?

Чтобы система ОВКВ равномерно распределяла необходимое количество воздуха по всему зданию, сертифицированный техник по расходу воздуха должен:

Используя сложные инженерные расчеты, распределите это число среди общего количества комнат, исходя из размера комнаты, местоположения, приборов в комнате и т. д. Это даст им воздушный поток в каждой комнате.

Изучите план здания, чтобы лучше понять расположение каждой комнаты и пути движения воздуха.

Осмотрите и запустите систему HVAC, чтобы убедиться, что она работает с оптимальной эффективностью.

С помощью специального оборудования снимите полученные показания расхода воздуха – во-первых, для всей системы, а во-вторых, для каждой комнаты в доме, чтобы сравнить их с требуемыми расчетами расхода воздуха, чтобы увидеть, нет ли расхождений.

После того, как несоответствия будут обнаружены, они могут исправить их с помощью воздушного баланса. Некоторые из вас, занимающихся своими руками, могут подумать: «Эй, я могу сделать это сам». Но это не самая сложная часть. Читайте дальше, чтобы узнать, как профессионалы могут помочь вам получить максимальную отдачу от вашей системы HVAC.

Как увеличить поток воздуха в воздуховоде с помощью заслонки HVAC

Итак, как опытные специалисты по HVAC увеличивают или уменьшают поток воздуха в вашем доме для достижения идеальной гармонии? Они:

1. Измените скорость вентилятора системы, чтобы увеличить или уменьшить общий выходной поток воздуха.
2. Осмотрите воздуховод на наличие повреждений или ослабления. Проблемы с конструкцией воздуховодов и/или проблемы с установкой являются причиной номер один, почему воздух не сбалансирован в жилых домах.
3. Добавьте или удалите подающие и возвратные воздуховоды , чтобы обеспечить подачу достаточного количества воздуха в каждую комнату.
4. Герметизировать или изолировать доступные неизолированные воздуховоды.
5. Добавьте заслонки к воздуховодам. Это направляет поток воздуха, исходящий от блока HVAC, и перемещает его на желаемую величину в каждую комнату. Некоторые воздуховоды уже оснащены заслонками и их можно просто отрегулировать.
6. Изменить настройки воздухоочистителя/блока фильтрации

После того, как эти флажки отмечены , , ваш воздух сбалансирован. Теперь вы, наверное, задаетесь вопросом – во сколько мне это обойдется? Продолжайте читать, и вы узнаете.

Сколько стоит балансировка воздуха?

Правда в том, что воздушный баланс намного сложнее, чем, скажем, очистка воздуховодов. Это связано с тем, что балансировка воздуха более сложна, требует больше времени, труда и специального оборудования.

Средняя стоимость балансировки воздуха зависит от таких факторов, как доступность и размер отверстий воздуховодов, и может варьироваться от 75 до 150 долларов за отверстие, что не включает добавление или удаление воздуховодов, их герметизацию и изоляцию. Допустим, в вашем доме есть один вытяжной вентилятор, один воздухозаборник, девять приточных отверстий и одно возвратное отверстие. Такой сертифицированный воздушный баланс будет стоить от 900 до 2000 долларов. И это может звучать как много, но это стоит вложений.

Что вы получите от системы Air Balance

Преимущества системы Air Balance

Возможно, вас не удивит, но балансировка воздуха в вашем доме имеет много преимуществ. Вот основные преимущества:

Постоянная температура

Очевидно, да, но это самая важная причина. Как объяснялось ранее, балансировка воздуха обеспечивает постоянный приток воздуха в каждую комнату внутри здания. Это означает, что вы можете превратить эту неиспользуемую свободную спальню в домашний офис своей мечты.

Повышенный комфорт

Чтобы в вашем доме было комфортно, температура в ваших комнатах должна соответствовать настройкам термостата. Балансировка воздуха обеспечивает оптимальный поток воздуха в этих комнатах и ​​из них, гарантируя, что вашим близким не будет слишком жарко или слишком холодно.

Лучшее качество воздуха

Сбалансированная система HVAC помогает защитить от неожиданного притока наружного воздуха, который часто несет с собой аллергены и примеси. Правильно герметизированное здание защищает отфильтрованный воздух внутри него, что так же важно для вашего здоровья, как фильтрация воды, которую вы пьете.

Повышенная энергоэффективность

Оптимизированная система HVAC означает сбалансированный поток воздуха по всему дому. Когда легко поддерживать равномерную температуру, системам HVAC не приходится перенапрягаться, работая в течение длительного периода времени, экономя ваши деньги и одновременно сохраняя землю.

Увеличенный срок службы систем ОВКВ

Для установок ОВКВ это нелегко. Они работают против крайностей в жаркую и холодную погоду, и суровые температуры сказываются на них. Чтобы поддерживать вашу систему HVAC в хорошем состоянии, главным приоритетом должно быть обеспечение баланса воздуха.

Не можете вынести боль от плохого воздуха? SuperTech сделает это лучше!

Позвоните своему местному специалисту по системам вентиляции и кондиционирования для получения информации о балансе воздуха

Ужасная правда заключается в том, что несбалансированный воздух создает нагрузку на вашу систему HVAC. Он изнашивается в течение продолжительных часов, что стоит вам денег и со временем приводит к увеличению затрат на ремонт и замену.

Итак, балансировка воздуха экономит вашу систему HVAC и ваши деньги. Хорошая компания HVAC будет работать с вами, чтобы должным образом оценить ваши потребности и предоставить вам доступное и долговечное решение, чтобы вы могли наслаждаться временем, которое вы проводите дома со своей семьей.