Урок в 9-м классе «Система уравнений, сводящихся к квадратным»
Цели урока:
- Повторить ранее изученные различные способы решения уравнений, сводящихся к квадратным.
- Научить сотрудничеству учеников посредством работы в малых группах, а так же взаимопомощи в процессе обучения. 3. Развитие познавательного интереса, интереса к педагогической деятельности.
Форма проведения: Работа в малых группах, с участием консультантов.
ХОД УРОКА
I. Организация начала урока.
Деление на группы
II. Сообщение учащимся цели предстоящей работы. Мотивация учения.
III. Интеллектуальная разминка. (Приложение 1)
Разминка в форме тестовых заданий. Подготовка к ЕГЭ.
IV. Проверка индивидуального домашнего задания, направленного на повторение основных понятий, основополагающих знаний, умений, способов действий. У доски работают консультанты. На предыдущем уроке им было задано индивидуальное домашнее задание.
Системы нелинейных уравнений, сводящихся к квадратным. (Приложение 2)
Решить систему уравнений
Решение: Если вычесть второе уравнение из первого, получим Значит надо решить систему уравнений
Из первого уравнения находим, что Подставляя х во
второе уравнение, получаем
откуда . Корнями этого квадратного уравнения служат . Если y1=3, то из находим х1=1. Если же .
Ответ:
Возможный способ оформления
Решим второе уравнение
Ответ:
Метод введения новых неизвестных при решении систем уравнений. (Приложение 3)
Решить систему уравнений
Решение. Обозначим через u, а через v. Тогда система примет вид
То есть получится система двух линейных уравнений с двумя неизвестными u и v. Из первого уравнения выражаем u через v: и подставляя во второе уравнение, получим , откуда v=2. Теперь находим u=1 и решаем уравнения
Ответ:
Возможный способ оформления
Пусть , тогда
Возвращаемся к переменным х и у.
Ответ:
Однородные уравнения. (Приложение 4)
Решить систему уравнений
Решение. Заметим, что для решений системы выполняется условие . В самом деле, из первого уравнения системы следует, что если , а числа не удовлетворяют второму уравнению системы. Разделим первое уравнение на . Получится уравнение
Введем вспомогательное неизвестное . Уравнение примет вид . Это квадратное уравнение, имеющее корни . Таким образом, из первого уравнения мы получаем, что либо либо . Осталось подставить выражения и (рассмотрев оба случая) во второе уравнение системы. В первом случае получится уравнение , откуда ; соответственно . Во втором случае получается уравнение , откуда ; соответственно
Ответ:
Возможный способ оформления
разделим первое уравнение на , получим
Пусть , тогда
Вернемся к переменным х и у.
Ответ:
V. Работа в малых группах.
Учащиеся получают задания на карточках и начинают работать в группах, обращаясь к консультантам за помощью при затруднениях.
Задания группам
Вариант 1
Решите систему уравнений
Задания группам
Вариант 2
Решите систему уравнений
VI. Подведение итогов урока.
VII. Задание на дом.
Задание по группам. Группа консультантов выполняет № 624 (4, 6, 8).
Для остальных № 623 (1, 3), № 624 (1, 3).
Таблица квадратов
Таблица квадратов или таблица возведения чисел во вторую степень. Интерактивная таблица квадратов и изображения таблицы в высоком качестве.
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 1 | 4 | 9 | 16 | 25 | 36 | 49 | 64 | 81 |
| 1 | 100 | 121 | 144 | 169 | 196 | 225 | 256 | 289 | 324 | 361 |
| 2 | 400 | 441 | 484 | 529 | 576 | 625 | 676 | 729 | 784 | 841 |
| 3 | 900 | 961 | 1024 | 1089 | 1156 | 1225 | 1296 | 1369 | 1444 | 1521 |
| 4 | 1600 | 1681 | 1764 | 1849 | 1936 | 2025 | 2116 | 2209 | 2304 | 2401 |
| 5 | 2500 | 2601 | 2704 | 2809 | 2916 | 3025 | 3136 | 3249 | 3364 | 3481 |
| 6 | 3600 | 3721 | 3844 | 3969 | 4096 | 4225 | 4356 | 4489 | 4624 | 4761 |
| 7 | 4900 | 5041 | 5184 | 5329 | 5476 | 5625 | 5776 | 5929 | 6084 | 6241 |
| 8 | 6400 | 6561 | 6724 | 6889 | 7056 | 7225 | 7396 | 7569 | 7744 | 7921 |
| 9 | 8100 | 8281 | 8464 | 8649 | 8836 | 9025 | 9216 | 9409 | 9604 | 9801 |
Таблица квадратов
02=0 12=1 22=4 32=9 42=16 52=25 62=36 72=49 82=64 92=81 | 102=100 112=121 122=144 132=169 142=196 152=225 162=256 172=289 182=324 19 2=361 | 202=400 212=441 222=484 232=529 242=576 252=625 262=676 272=729 282=784 292=841 | 302=900 312=961 322=1024 332=1089 342=1156 352=1225 362=1296 372=1369 382=1444 392=1521 | 402=1600 412=1681 432=1849 442=1936 452=2025 462=2116 472=2209 482=2304 492=2401 |
502=2500 512=2601 522=2704 532=2809 542=2916 552=3025 562=3136 572=3249 582=3364 592=3481 | 602=3600 612=3721 622=3844 632=3969 642=4096 652=4225 662=4356 672=4489 682=4624 692=4761 | 702=4900 712=5041 722=5184 732=5329 742=5476 752=5625 762=5776 772=5929 782=6084 792=6241 | 802=6400 812=6561 822=6724 832=6889 842=7056 852=7225 862=7396 872=7569 882=7744 892=7921 | 902=8100 912=8281 922=8464 932=8649 942=8836 952=9025 962=9216 972=9409 982=9604 992=9801 |
Теория
Квадрат числа – это результат умножения числа само на себя. Операция вычисления квадрата числа – это частный случай возведения числа в степень, в данном случае во вторую:
62 = 6 × 6 = 36
Данное выражение читается: «возвести в квадрат число 6» или «6 в квадрате».
Скачать таблицу квадратов
- Нажмите на картинку чтобы посмотреть в увеличенном виде.
- Нажмите на надпись «скачать», чтобы сохранить картинку на свой компьютер. Изображение будет с высоким разрешением и в хорошем качестве.
ЗРК 2К12 КУБ. Фото. Видео. ТТХ. Состав
Предназначен для противовоздушной обороны войск от самолетов, самолетов-снарядов, летящих на малых и средних высотах как с дозвуковыми, так и со сверхзвуковыми скоростями. ЗРК 2К12 “КУБ” и его модификации (2К12М1, 2К12М2 2К12МЗ) серийно выпускались в течение семидесятых годов и до настоящего времени находятся на вооружении армий России и многих зарубежных стран. В настоящее время для более эффективной борьбы с современными и перспективными средствами воздушного нападения (аэродинамическими и ракетными) комплекс 2К12 и его модификации принципиально модернизируются, им придаются новые качества, существенно улучшающие тактико-технические характеристики.
ЗРК 2К12 КУБ — видео
Осуществляется повышение ЗРК КУБ:
— надежности путем перевода блоков и узлов на современную элементную базу российского производства, а также предложенную инозаказчиком;
— возможности централизованного управления ЗРК путем введения в его состав новых средств централизованного управления, а также сопряжение ЗРК со средствами централизованного управления, стоящими на вооружении у инозаказчика.
В 1996-1998 годах проведена модернизация ЗРК «Квадрат». В ЗРК были введены:
— цифровая обработка сигналов селекции движущихся целей;
— новый передатчик подсвета целей;
— система распознавания класса целей;
— режим регламентации излучения:
— режим сопровождения целей с помощью телевизионно-оптического визира.
В 1999-2000 годах в соответствии с согласованным техническим заданием модернизация ЗРК «Квадрат» и его модификаций, поставленных на экспорт, будет проводиться по указанным направлениям. Цель модернизации — создание ЗРК с улучшенными техническими и эксплуатационными характеристиками -2К12М5 (ЗРК «Квадрат-М»). Модернизации подлежат боевые, технические средства и средства управления огнем ЗРК.
Боевые средства модернизированного ЗРК «Квадрат-М» предполагается иметь в составе:
— модернизированной самоходной установки разведки и наведения — СУРН 1С91М2Э;
— четырех модернизированных самоходных пусковых установок — СПУ 2П25М2Э;
— одной самоходной огневой установки — СОУ 9А310М1 из состава ЗРК 9К37М1 “Бук-М1”, доработанной для стыковки с СУРН и СПУ и обеспечивающей работу либо трех ЗУР ЗМ9МЗ, либо четырех ЗУР ЗРК ”Бук-М1-2″;
— ракет ЗРК «Бук-М1-2» (до четырех штук), размещаемых на СОУ;
— мобильной пассивной станции автоматического обнаружения источников радиоизлучения «Орион» (85В6), позволяющей производить обнаружение излучающих объектов-целей. «Орион» обеспечивает автоматический панорамный обзор пространства, обработку сигналов с помощью ЦВС, передачу информации на СУРН в виде целеуказания (ЦУ) по АЗ и УМ в аналоговой форме через КПЦ или непосредственно. «Орион» монтируется на мобильной базе (автомобиль УАЗ), обслуживается одним человеком. Источник питания — автономный. Количество целей, по которым может быть выдана информация пользователю — 30-50. СОУ может придаваться одна СПУ 2П25М2Э с возможностью обеспечения управления огнем с СОУ или одна ПЗУ 9А39 с восемью ракетами ЗРК «Бук-M1-2».
Cамоходная установка разведки и наведения 1С91
Тип и состав боевых средств ЗРК «Квадрат-М» может определяться инозаказчиком
В состав модернизированных средств управления огнем ЗРК «Квадрат-М” предполагается ввести:
— модернизированный комплект аппарата К-1 «Краб»;
— пункт боевого управления (ПБУ) — изделие 9С470М1 (КП) из состава комплекса «Бук-М1»;
— пост обработки радиолокационной информации (ПОРИ) 9С467-2ВМ2.
Предполагается замена РЛС дальнего обнаружения типа П-40, П-18( 12) П-19(15) в составе «Краб” на современную станцию обнаружения целей (СОЦ) типа 9С18 с фазированной антенной решеткой, сопрягаемой с ПБУ 9С470М1 и далее с СОУ 9А310М1 посредством системы теле-кодовой связи.
Тип и состав вышеуказанных средств управления также определяется инозаказчиком.
В состав технических средств ЗРК «Квадрат-М1” дополнительно к имеющимся включаются:
— транспортная машина 9Т243 для транспортировки ракет;
— автоматизированная контрольно-испытательная подвижная станция 9В95М1 для контроля ракет;
— мастерская технического обслуживания 9В881М1.
В результате модернизации ЗРК «Квадрат» и его модификаций предполагается получить следующие боевые и технические характеристики комплекса «Квадрат-М»:
— увеличение боевой производительности в 1,8-2 раза:
— увеличение помехозащищенности и скрытности работы;
— увеличение зоны поражения по высоте в 1,5-1,8 раза, по дальности в 1,3-1,7 раза;
— увеличение количества одновременно обстреливаемых целей до двух;
— значительное расширение парка поражаемых целей.
Увеличение боевой производительности обеспечивается за счет параллельной работы двух стрельбовых каналов (СУРН 1С91М2Э — СПУ 2П25М2Э и СОУ 9А310М1 -СПУ). Увеличение помехозащищенности и скрытности работы ЗРК «Квадрат-М» обеспечивается за счет высокой помехозащищенности СОУ 9А310М1 и бортовой аппаратуры ракет ЗРК «Бук-М1», за счет введения в состав СУРН 12-литерного передатчика подсвета целей и цифровой селекции движущихся целей (ЦСДЦ) и применения станций «Орион».
Увеличение зоны поражения ЗРК «Квадрат-М» обеспечивается самостоятельной работой канала СОУ 9А310М1 в автономном режиме до:
— по высоте от 15 м до 22000 м для ракеты ЗРК «Бук-М1 -2»;
— по дальности от 3 км до 40 км для ракеты 9М317, Vu = 830 м/с и Нц = 10000 м;
— по дальности от 3 км до 22 км Нц = 50-100 м для ракет ЗРК «Бук-М1-2”.
Модернизированный ЗРК «Куб-М» может обеспечить поражение самолетов тактической и стратегической авиации, тактических баллистических ракет с дальностью пуска 50-150 км (ракетой ЗРК «Бук-М1-2»), крылатых авиационных ракет типа АЛКМ, «Мейверик» и «Харм», УАБ типа «Уоллай», вертолетов и ДПЛА, а также надводных целей типа катер и фрегат (ракетами ЗРК «Бук-М1-2») и наземных РД целей.
Вероятность поражения ЗРК «Куб-М» при стрельбе одной ракетой ЗРК «Бук-М1-2» для различных типов целей составит 0,7-0,95.
Вероятность поражения не ухудшается более чем на 15-20 процентов при постановке помех системам наведения ракет.
Модификации ЗРК Куб
2К12Е «Квадрат»
Экспортная модификация комплекса 2К12 «Куб». Создана в 1971 году. Основными отличиями от базового варианта является изменённая система распознавания государственной принадлежности целей, изменённый уровень помехозащищённости и возможность работы в тропических условиях.
2К12М «Куб-М»
После принятия на вооружение ЗРК 2К12, началась работа по его модернизации. В 1968 году был разработан комплекс 2К12М «Куб-М». Модернизированный комплекс имел возможность поражения целей маневрирующих с перегрузками до 5—6 g. Нижняя граница поражения была уменьшена со 100 до 50 метров, а дальность поражения была увеличена на 20 % благодаря усовершенствованию излучателя.
2К12М1 «Куб-М1»
В январе 1973 года был принят на вооружение модернизированный комплекс 2К12М1 «Куб-М1». В результате доработок были расширены границы зоны поражения целей, улучшена защищённость головки самонаведения от помех, работное время уменьшено приблизительно на 5 секунд, улучшена надёжность всех средств комплекса, а также предусмотрена прерывистая работа РЛС СУРН 1С91 для противодействия противорадиолокационным ракетам типа AGM-45 Shrike.
2К12М3 «Куб-М3»
В 1974—1975 гг. была проведена дальнейшая модернизация комплекса 2К12. В конце 1976 года на вооружение поступил ЗРК 2К12М3 «Куб-М3». По сравнению с предыдущими вариантами 2К12М3 имел расширенные границы зоны поражения, появилась возможность вести стрельбу «вдогон» по целям со скоростями до 300 м/с, средняя скорость полёта ЗУР увеличена до 700 м/с, появилась возможность поражения самолётов маневрирующих с перегрузками до 8 g, улучшена помехозащищённость головки самонаведения, ближняя граница зоны поражения уменьшена, вероятность поражения целей увеличена на 10—15 %.
2К12М3С «Куб-М3С»
В 1970-е годы активно велись разработки в области радиоэлектронной борьбы. Советские разработки эффективно противодействовали иностранным ЗРК типа MIM-23 Hawk. В целях снижения восприимчивости 2К12 к подобным средствам потенциального противника, была разработана модификация 2К12М3С. Новая модификация имела защиту от средств радиоэлектронной борьбы типа «Смальта». В 1979 году комплекс 2К12М3С был принят на вооружение.
2К12М3А «Куб-М3А»
Последняя модернизация комплекса 2К12 была проведена в 1981 году. В комплексе использовалась новая модифицированная ракета 3М9М4 с массой боевой части в 70 кг, однако, комплекс на вооружение принят не был. Основной причиной отказа от 2К12М3А стало принятие на вооружение нового более перспективного комплекса 9К37 «Бук».
2К12М4 «Куб-М4»
В 1972 году были начаты работы по созданию нового ЗРК 9К37 «Бук». Принять на вооружение комплекс планировалось в 1975 году, для ускорения работ, принятие на вооружение было решено разделить на два этапа. Первый этап предусматривал введение в состав комплекса 2К12 «Куб-М3» самоходной огневой установки 9А38 с ракетами 9М38 в каждую батарею. Благодаря введению СОУ 9А38 количество целевых каналов увеличилось с 5 до 10, а боеготовных ЗУР с 60 до 75. В таком виде в 1978 году на вооружение был принят ЗРК 2К12М4 «Куб-М4».
Состав батарейного комплекса 2К12М4 «Куб-М4» (9К37-1 ЗРК «Бук-1»)
— 1 × СУРН 1С91М3 (из состава ЗРК «Куб-М3»)
— 4 × СПУ 2П25М3 (из состава ЗРК «Куб-М3»)
— 1 × СОУ 9А38 (из состава ЗРК «Бук») с ракетами 9М38 или с ракетами 3М9М3.
В состав зенитно-ракетного полка входят 5 стартовых батарей и батарея управления, а также вспомогательные подразделения.
Тактико-технические характеристики ЗРК Куб-М4
Зона поражения ЗРК Куб-М4
— по дальности: 4-24 км
— по высоте: 0,03-14 км
— по параметру: до 18 км
— Вероятность поражения истребителя одной ЗУР: вертолета 0,3-0,6; крылатой ракеты 0,25-0,5
— Макс скорость поражаемых целей, м/с: 600
— Время реакции, с: 24
— Скорость полета ЗУР, м/с: 700
— Масса ракеты, кг: 630
— Масса боевой части, кг: 57
— Канальность по цели: 2
— Канальность по ЗУР: до 3
— Время развертывания (свертывания), мин: 5
— Число ЗУР на боевой машине: 3
— Год принятия на вооружение: 1978
Фото ЗРК 2К12 КУБ
You have no rights to post comments
| 1. | Метод сложения (линейные уравнения) | 1 вид — рецептивный | лёгкое | 2 Б. | Решение системы уравнений методом алгебраического сложения. |
| 2. | Метод подстановки (линейные уравнения) | 1 вид — рецептивный | лёгкое | 2 Б. | Решение системы двух линейных уравнений. |
| 3. | Корни квадратного уравнения, теорема Виета | 1 вид — рецептивный | лёгкое | 2 Б. | Составление квадратного уравнения. |
| 4. | Метод подстановки (линейное и квадратное) | 1 вид — рецептивный | лёгкое | 2 Б. | Решение системы уравнений. |
| 5. | Метод алгебраического сложения | 2 вид — интерпретация | среднее | 4 Б. | Решение системы уравнений методом алгебраического сложения. |
| 6. | Способ сложения | 2 вид — интерпретация | среднее | 4 Б. | Решение системы методом сложения. |
| 7. | Пары чисел, которые являются решением системы уравнений | 2 вид — интерпретация | среднее | 4 Б. | Выбор пар чисел, которые являются решением системы уравнений. |
| 8. | Графический метод (парабола и прямая) | 2 вид — интерпретация | среднее | 4 Б. | Решение системы двух уравнений графическим методом. |
| 9. | Графический метод (гипербола и прямая) | 2 вид — интерпретация | среднее | 4 Б. | Решение системы двух уравнений графическим методом. |
| 10. | Графический метод (элементарные функции) | 2 вид — интерпретация | среднее | 3 Б. | Изобразив схематически графики уравнений, выяснить, сколько решений имеет система уравнений. |
| 11. | Система квадратных уравнений | 2 вид — интерпретация | среднее | 4 Б. | Решение системы квадратных уравнений методом сложения. |
| 12. | Система уравнений (линейное и квадратное) I | 2 вид — интерпретация | среднее | 4 Б. | Решение системы уравнений (линейное и квадратное) методом подстановки. |
| 13. | Система уравнений (линейное и квадратное) II | 2 вид — интерпретация | среднее | 4 Б. | Решение системы уравнений (линейное и квадратное) методом подстановки. |
| 14. | Система уравнений (линейное и квадратное) III | 2 вид — интерпретация | среднее | 3 Б. | Решение системы уравнений (линейное и квадратное) методом подстановки, использование формулы разности квадратов. |
| 15. | Задача на составление системы уравнений | 2 вид — интерпретация | среднее | 4 Б. | Текстовая задача на составление системы уравнений, которая решается методом подстановки. |
| 16. | Система рациональных уравнений | 2 вид — интерпретация | среднее | 4 Б. | Решение системы рациональных уравнений методом введения новых переменных. |
| 17. | Система, состоящая из рационального и квадратного уравнений | 2 вид — интерпретация | среднее | 4 Б. | Решение системы, состоящей из квадратного и рационального уравнений, методом введения новой переменной. |
| 18. | Система, состоящая из рационального и линейного уравнений | 2 вид — интерпретация | среднее | 3 Б. | Решение системы, состоящей из рационального и линейного уравнений, методом введения новой переменной. |
| 19. | Система рациональных уравнений, вводится одна новая переменная | 2 вид — интерпретация | среднее | 4 Б. | Решение системы, состоящей из рациональных уравнений, методом введения новой переменной. |
| 20. | Система, состоящая из рациональных уравнений | 2 вид — интерпретация | среднее | 4 Б. | Решение системы рациональных уравнений методом введения новой переменной. |
| 21. | Система, состоящая из квадратного и рационального уравнений | 2 вид — интерпретация | среднее | 3 Б. | Решение системы, состоящей из квадратного и рационального уравнений, методом введения новой переменной. |
| 22. | Система линейных уравнений | 2 вид — интерпретация | среднее | 4 Б. | Решение системы линейных уравнений графическим методом. |
| 23. | Система, состоящая из квадратного и рационального уравнений, метод умножения | 2 вид — интерпретация | среднее | 3 Б. | Решение системы, состоящей из квадратного и рационального уравнений, методом введения новой переменной, также используется метод умножения. |
| 24. | Пары чисел, которые являются решением системы уравнений | 2 вид — интерпретация | среднее | 6 Б. | Выбор пар чисел, которые являются решением системы уравнений. |
| 25. | Графический метод (окружность и парабола) | 3 вид — анализ | сложное | 3 Б. | Выяснение, при каком значении параметра система уравнений имеет одно или три решения. |
Квадрат Декарта как техника принятия решений

Нынешний век является веком высоких технологий, суперсовременных разработок и бешеного ритма жизни. Ежедневно жизнь сталкивает нас лицом к лицу с необходимостью решения огромного количества задач, для чего нам приходится постоянно размышлять над тем, какой выбор стоит сделать в каждой отдельно взятой ситуации. И размышляя над тем, каким пойти путём, все мы используем какие-то свои навыки, методы и техники принятия решений, которые основываются, главным образом, на нашем жизненном опыте, мнениях, позициях, взглядах, точках зрения. Но всегда ли наши способы принятия решений хороши и эффективны? Можно с уверенностью сказать, что далеко не всегда.
Техника принятия решений, о которой мы поговорим в этой статье, конечно, не является волшебной, однако настолько адаптивна и проста в использовании, что считается, пожалуй, одной из самых лучших, имеющихся на сегодняшний день. Называется она «Квадратом Декарта».
Чтобы не возникало лишних вопросов, следует сказать, что автором данной техники является Рене Декарт – французский философ, физиолог, физик, механик, математик, а также основоположник алгебраической символики и аналитической геометрии и автор философского метода радикального сомнения.
Квадрат Декарта
Квадрат Декарта является предельно простой техникой принятия решений, которая требует для своего использования очень небольшого количества времени. При помощи Квадрата Декарта легко установить наиболее значимые критерии выбора, а также оценить последствия любого варианта принимаемого решения.
Если взглянуть на жизнь обычного человека, то можно увидеть, что когда он оказывается в ситуации, где необходимо принимать решения, он, как правило, концентрируется на одной или двух его особенностях, тем самым загоняя себя в своеобразный тупик, в котором не замечаются другие значимые критерии выбора. Кроме того, стандартное мышление человека способствует тому, что он задаёт себе всего лишь один вопрос: «Что будет, если это произойдёт?», ведь обычный сценарий поведения подразумевает выполнение какого-либо действия и оценку последующей за ним обратной связи. Но на практике уже было сотни раз доказано, что в первую очередь необходимо сначала основательно подумать и только после этого выполнять действие. И Квадрат Декарта как раз и рассчитан на то, чтобы сначала подумать, но не просто перебрать в голове несколько вариантов, а расписать всё на бумаге, следуя определённой технологии.
В качестве примера можно привести следующую ситуацию: вы хотите сменить род деятельности (устроиться на новую работу, заняться своим бизнесом, уйти во фриланс и т.д.), но никак не можете избавиться от сомнений на этот счёт. Вы, конечно, видите все плюсы и преимущества нового вида деятельности, но не знаете, что это такое – заниматься тем, чем вы ещё не занимались, и, соответственно, колеблетесь в принятии решения. Так вот: используя Квадрат Декарта, вы можете посмотреть на сложившуюся ситуацию с четырёх разных сторон (продолжим рассмотрение этого примера чуть позже).
Как пользоваться Квадратом Декарта?
Для использования Квадрата Декарта вам понадобится листок бумаги, ручка или карандаш. Как только эти инструменты будут готовы, вы можете приступать к работе с Квадратом, которая подразумевает ответы на четыре основных вопроса. Эти четыре вопроса можно образно представить как четыре пункта наблюдения за проблемой, с которых можно рассмотреть проблему с разных сторон и получить о ней наиболее объективное представление. И ещё: очень важно дать на каждый из четырёх вопросов как можно большее количество ответов, т.к. это позволит рассмотреть максимальное количество особенностей проблемы.
Итак, Квадрат Декарта выглядит следующим образом:

Задаём себе последовательно четыре вопроса и отвечаем на них следующим образом:Для наглядного рассмотрения принципа работы Квадрата Декарта давайте возьмём тот же пример с изменением рода деятельности, который мы рассматривали выше.
Что случится, если это произойдёт?
Данный вопрос подразумевает поиск плюсов от получения желаемого. Под словом «это» следует иметь в виду реализацию принимаемого решения. Первый вопрос является наиболее очевидным и по этой причине очень важно находить как можно больше ответов, т.е. не останавливаться на том, что первым приходит на ум. Ответы на этот вопрос будут служить вам мотивацией к принятию решения.
Что случится, если я поменяю род деятельности?
- Если я поменяю род деятельности, я сделаю первый шаг к своей мечте – заниматься тем, чем мне действительно нравится.
- Если я поменяю род деятельности, я смогу перестать работать «на дядю» и сам контролировать и свою работу, и свой доход.
- Если я поменяю род деятельности, это скажет о моей смелости, и я стану больше уважать самого себя.
- Если я поменяю род деятельности, я смогу доказать тем, кто меня окружает, что серьёзно намерен изменить свою жизнь.
- Если я поменяю род деятельности, это станет моей мотивацией к получению новых знаний, овладению новыми навыками.
- Если я поменяю род деятельности, смогу скорее начать заниматься чем-то новым.
- Если я поменяю род деятельности, я перестану сомневаться насчёт правильности своего выбора.
Что случится, если это НЕ произойдёт?
Данный вопрос подразумевает поиск плюсов от неполучения желаемого. Другими словами, ответы на второй вопрос покажут вам, что случится, если вы откажетесь от реализации принимаемого решения, и всё останется так же, как и было раньше. Отвечая, записывайте все преимущества настоящего положения дел, которые вы не хотели бы потерять.
Что случится, если я не поменяю род деятельности?
- Если я не поменяю род деятельности, мне не нужно будет отказываться от привычного образа жизни.
- Если я не поменяю род деятельности, я не буду переживать по поводу того, что придётся осваивать новые знания и учиться новым вещам, ведь это может не получиться.
- Если я не поменяю род деятельности, я смогу спокойно отдыхать в свои выходные дни.
- Если я не поменяю род деятельности, мне не нужно будет ни перед кем объясняться или оправдываться.
- Если я не поменяю род деятельности, я смогу подумать об этом в будущем. Возможно, действительно стоит повременить.
- Если я не поменяю род деятельности, я смогу предаваться грёзам о том, как занимаюсь тем, что мне действительно нравится.
- Если я не поменяю род деятельности, я докажу окружающим меня людям, что меня устраивает текущее положение дел.
Чего НЕ случится, если это произойдёт?
Данный вопрос подразумевает поиск минусов от получения желаемого. Проще говоря, ответы на третий вопрос будут представлять собой ту цену, которую вы должны будете заплатить за реализацию принимаемого решения.
Чего не случится, если я поменяю род деятельности?
- Если я поменяю род деятельности, я уже не смогу жить той жизнью, к которой так привык за много лет.
- Если я поменяю род деятельности, я уже не смогу откладывать действия по поиску новых возможностей.
- Если я поменяю род деятельности, я уже не смогу отдыхать в привычные для меня выходные дни.
- Если я поменяю род деятельности, у меня уже не будет достаточного количества времени на бесцельное, но приятное времяпрепровождение.
- Если я поменяю род деятельности, у меня уже не будет возможности общаться с прежними коллегами и ходить на весёлые корпоративы.
- Если я поменяю род деятельности, ко мне уже не будет прежнего отношения окружающих меня людей.
Чего НЕ случится, если это НЕ произойдёт?
Данный вопрос подразумевает поиск минусов от неполучения желаемого. Отвечая на четвёртый вопрос, вы отсекаете оставшиеся «не», мешающие реализации принимаемого решения. На этом этапе рекомендуется отвечать как можно быстрее, опираясь на интуицию.
Чего не случится, если я не поменяю род деятельности?
- Если я не поменяю род деятельности, у меня не появится возможности реализовать свою мечту – зарабатывать, занимаясь тем, что мне действительно нравится.
- Если я не поменяю род деятельности, я не смогу перестать работать «на дядю», а значит, не смогу самостоятельно контролировать свою работу и свой доход.
- Если я не поменяю род деятельности, я не стану больше уважать себя, т.к. покажу страх перед переменами в жизни.
- Если я не поменяю род деятельности, никто (в том числе и я сам) не поверит в серьёзность моих намерений изменить жизнь.
- Если я не поменяю род деятельности, у меня так и не появится мотивации к получению новых знаний и овладению новыми навыками.
- Если я не поменяю род деятельности, я не смогу избавиться от своих сомнений и так и останусь в переживаниях по поводу того, что не принял решения.
На самом деле, применять Квадрат Декарта можно не только к сфере профессиональной деятельности, но и к любой другой области жизни. Но важно раз и навсегда уяснить, что все свои ответы нужно именно записывать, а не отвечать мысленно. Во-первых, вы можете просто запутаться в своих ответах, а во-вторых, подсознание человека работает таким образом, что игнорирует частицу «НЕ», по причине чего велика вероятность допущения ошибок. Поэтому, обязательно используйте листок и ручку, можно даже распечатать Квадрат в большом формате, и отвечать на каждый из вопросов в соответствующем секторе. А сам процесс записи ответов будет как бы конвертировать мысленные доводы и фантазии в логическую буквенную форму, что и окажет вам существенную помощь в принятии решения.
Квадрат Декарта — одна из многочисленных техник, глобально применяемых для управления временем. Больше таких техник мы разбираем на курсе «Лучшие техники тайм-менеджмента». Присоединяйтесь!
Квадранты Кови (матрица Эйзенхауэра): просто о планах
Прочитано: 20 869
Почему рушатся планы? Потому что в потоке повседневных дел мы стремимся к выполнению срочных дел, забывая о важных и обязательных. В чем разница? В правильности приоритетов! Не всегда важные дела являются срочными, а срочные – важные. Как так? Очень просто. И разобраться с этим помогут «квадранты Кови». Второе их название – матрица приоритетов Эйзенхауэра.
Важно и срочное: термины и уточнения
Чтобы понять, о чем именно пойдет речь дальше, нужно дать расшифровку двум понятиям.
Важность и Срочность.
Срочные дела требуют немедленного, незамедлительного участия или решения. Их надо делать моментально, иначе случится пожар, форс-мажор, катастрофа. Срочные дела нуждаются в реактивном реагировании, заставляя отменять все планы и важные дела.
Важные дела подразумевают проактивный подход. Они нужны для достижения поставленных глобальных целей, предварительного решения важных задач, реализации возможностей. Занимаясь выполнением важных дел, человек достигает высоких результатов, успешности. Жизнь протекает четко, размеренно и целеустремленно.
К сожалению, важные дела в нашей жизни часто лишены приоритетного значения. Почему? Потому что вся повседневность направлена на решение срочных задач.
Как это исправить?
Использовать матрицу Эйзенхауэра как инструмент расстановки приоритетов. Иногда для этой же цели рекомендуют квадраты времени Кови.
Чем различаются матрица квадрантов Стивена Кови и матрица дел Эйзенхауэра?
Собственно, ничем.
Оба метода подразумевают идентичные подходы к планированию. А разные названия получили из-за знаменитых разработчиков систем. Так уж получилось, что Дуайт Эйзенхауэр использовал в повседневной работе ту же технику, что описал в своей книге Стивен Кови.
Два великих человека. Два названия. Один метод.
Квадранты Кови: матрица структуры дел
Расстановка приоритетов по матрице Эйзенхауэра подразумевает градирование всех дел и задач на 4 блока по их важности и срочности выполнения:
- важное/срочное;
- важное/несрочное;
- неважное/срочное;
- неважное/несрочное.
Если сделать предварительно выгрузку дел – выписать все ближайшие и далекие дела в один список, то можно легко заполнить любой квадрат Стивена Кови. Достаточно оценить значимость и срочность всех имеющихся задач.
Как делить задачи по матрице Эйзенхауэра?
- Блок А – Важное/Срочное. Это дела-пожары, требующие незамедлительного решения. Это отчет, который нужно было сдать начальнику вчера. Подготовка к контрольной, которая начнется через час. Больной зуб, нуждающийся в лечении.
- Блок B – Важное/Несрочное. Сюда обычно попадают стратегические задачи. Их нужно и важно делать, но заниматься этим необязательно сегодня. В качестве примера можно использовать выполнение плана по заполнению сайта, изучение иностранного языка, пробежка по утрам.
- Блок С – Неважное/Срочное. Этому квадранту матрицы Эйзенхауэра соответствуют все популярные хронофаги: звонки с просьбами что-то сделать; статья, которую посоветовали прочитать, поиск псевдоважных вещей и решение псевдоважных задач. То есть мы-то считаем, что решаемые задачи важны, но на деле их можно легко отложить или даже делегировать.
- Блок D – Неважное/Несрочное. Список в этом квадранте может быть очень большим, но чаще всего это «развлекательно-увлекательные» дела.
Высокоэффективный тайм-менеджмент по матрице Эйзенхауэра
Если посмотреть на структуру каждого блока непредвзято, то видны особенности каждого квадрат:
- Квадрат A – постоянный цейтнот, «пожар», нервы и реактивный ритм жизни.
- Квадрат B – решение стратегических задач, проактивность, работа на результат и успех.
- Квадрат C – хронофаги в их разных вариантах.
- Квадрат D – прокрастинация.
То есть при определении приоритетов с помощью матрицы Эйзенхауэра внимания заслуживают только дела второго блока. А по факту занимаемся мы задачами «срочных» квадратов», тратя нервы и отвлекаясь на ненужные факторы.
Что делать с этими знаниями?
Все очень просто. Планирование времени в соответствии с матрицей Эйзенхауэра подразумевает проактивный подход и применение лучших инструментов тайм-менеджмента.
Использовать можно:
Практически все из них в той или иной степени позволят грамотно распределить квадраты времени Стивена Кови в повседневной жизни и отказаться от ненужных и бессмысленных занятий.
Матрица Эйзенхауэра для домохозяек
Есть и упрощенная матрица Эйзенхауэра для домохозяек. Ее особенность – концентрация на домашних делах и рутине.
Градация и понимание квадратов могут быть примерно следующие:
- Б – важные и несрочные. Большинство текущих дел с детьми и по дому.
- А – форс-мажоры, которые нужно решать. А чтобы их было меньше, нужно меньше реагировать на обстоятельства и четче придерживаться бытовых планов.
- С – отвлечения всех видов, которые нужно контролировать и держать в узде.
- D – бессмысленное времяпровождение, которое легко заменить заслуженным запланированным отдыхом после выполнения дел.
Кто-то думает, что домохозяйкам не нужно планирование и четкий график. Все наоборот.
Бесконечно занятые собой и детьми женщины более чем кто другой нуждаются в правильной структуре дня.
Матрица срочности и важности матрица Эйзенхауэра – удобное упражнение, помощник и советчик на каждый день. Использование квадрантов Кови значительно снижает уровень стресса в повседневной жизни и делах.
Интересные статьи:
Психоматрица по дате рождения(Квадрат Пифагора)
Психоматрица по дате рождения(Квадрат Пифагора)
Не пытайтесь изменить мир или окружающих вас людей, измените сначала себя. Когда вы измените себя, изменятся и окружающие вас люди, изменится мир. © Ключи к жизни
Психоматрица Астрология Онлайн гадания Карты судеб Нумерология Лунный календарь Парапсихология Гороскопы Интересное Настройки сайтаКвадрат Пифагора — это отдельное направление нумерологии. По сути это учение берет свое начало от египетских жрецов. Именно они одни из первых начали сопоставлять качества характера человека в зависимости от чисел. Пифагор взял за основу эти знания о числах и применил к ним математический аспект, основанный на гармонии квадрата.
Пифагор и его последовали расширили возможности египетской системы, дополнив значения отдельных цифр значениями целевых линий квадрата Пифагора. Таким образом новое учение помогало выявить возможную цель жизни человека.
Приложение Квадрат Пифагора от Tragos.ru Дата рождения
Дата рожденияДень:12345678910111213141516171819202122232425262728293031
Месяц:ЯнварьФевральМартАпрельМайИюньИюльАвгустСентябрьОктябрьНоябрьДекабрь
Год:202020192018201720162015201420132012201120102009200820072006200520042003200220012000199919981997199619951994199319921991199019891988198719861985198419831982198119801979197819771976197519741973197219711970196919681967196619651964196319621961196019591958195719561955195419531952195119501949194819471946194519441943194219411940193919381937193619351934193319321931193019291928192719261925192419231922192119201919191819171916191519141913191219111910190919081907190619051904190319021901
Поделиться ссылкой с друзьями Сегодня 7 августа 2020 г.Карта дня: 6 ♦
Быстрый гороскопУзнайте о сборах Square | Центр поддержки Square
Комиссия компании Square за обработку платежей
Примечание. Если вам не удается загрузить приложение Square после обновления операционной системы устройства, возможно, ваше устройство не поддерживается. Узнайте больше об устройствах, поддерживаемых Square. Если вы переводите свой бизнес на онлайн-торговлю, загляните в интернет-магазин Square.
СборыSquare по типу платежа
КомиссияSquare за обработку вычитается до того, как средства будут переведены на ваш связанный банковский счет.Вот типы платежей, которые вы можете принять с помощью Square, и связанные с ними комиссии на общую сумму транзакции:
* Более высокая комиссия за вводимые вручную транзакции связана с большим риском, связанным с этими платежами, поскольку ни платежная карта, ни владелец карты не должны присутствовать для проведения платежа.
Есть несколько тарифных планов для Square Online Store. Выберите лучший ценовой уровень, соответствующий потребностям вашего онлайн-бизнеса.
Вы не будете платить комиссии за следующие типы платежей:
Щелкните здесь, чтобы узнать больше о том, как работают сборы за обработку.
Факты, которые необходимо знать о комиссиях Square за обработку платежей
- Никаких скрытых комиссий! Нет комиссии за:
- Активация
- Загрузка приложения Square Point of Sale
- Возвратные платежи и управление спорами
- Квадратная опора
- Возврат
- Расширенные инструменты отчетности
- Бездействие аккаунта
- Соответствие PCI Покрытие соответствия PCI
- Защита от захвата аккаунта
- Сквозное шифрование платежей
- Активное предотвращение мошенничества
- Переводы на следующий рабочий день
- Free Square Reader для магнитной полосы
- Досрочное прекращение
- Комиссии по кредитной карте включены в комиссию Square, поэтому компании, выпускающие кредитные карты, не взимают комиссии.
- У всех принимаемых марок карт одинаковая ставка.
- Комиссия за обработку платежей вычитается из общей суммы каждой транзакции, включая налоги и чаевые. Комиссии
- Square распространяются на все типы бизнеса, включая некоммерческие организации.
- Узнайте больше о том, как распределяются наши сборы.
Особые ставки сборов за обработку
Если ваш годовой объем продаж превышает 250 000 долларов США, а средний размер чека превышает 15 долларов США, свяжитесь с нашим отделом продаж.Мы поможем подобрать для вас подходящую скорость транзакции. Свяжитесь с отделом продаж.
Просмотрите свои комиссии
Просматривайте текущие показатели обработки в любое время из Расценки и подписки на онлайн-панели Square Dashboard.
Примечание: Если у вас более одного местоположения, вы должны сначала выбрать местоположение, чтобы просмотреть его ставки.
Просмотр комиссий, уплаченных за перевод
В приложении Square Point of Sale:
- Коснитесь трех горизонтальных линий> коснитесь Баланс .
- Нажмите Отчеты о передаче > выберите передачу.
- Сборы за продажи, включенные в эту передачу, перечислены в разделе Сборы .
Из вашей онлайн-панели Square:
- Посетите Баланс > Отчеты о переводе на онлайн-панели Square Dashboard.
- Выберите диапазон дат с помощью инструмента выбора даты в верхнем левом углу.
- Выберите перевод из списка, чтобы просмотреть общую уплаченную комиссию.
- Чтобы просмотреть комиссии, связанные с каждой транзакцией в выбранном диапазоне дат переноса, щелкните Экспорт непосредственно под кнопкой диапазона дат.
Просмотр сборов за период времени
Просмотр комиссии за карточные платежи.
В приложении Square Point of Sale:
- Коснитесь трех горизонтальных линий> коснитесь Отчеты .
- Коснитесь Продажи > выберите предварительно определенный диапазон дат или коснитесь даты, чтобы установить настраиваемый диапазон.
- Tap Готово .
- Прокрутите до строки Сборы сводного отчета о продажах.
Из вашей онлайн-панели Square:
- В разделе Sales вашей онлайн-панели Square Dashboard щелкните Reports .
- Щелкните Сводка продаж > выберите диапазон дат с помощью инструмента выбора даты в верхнем левом углу.
- Комиссионные, уплаченные за этот период времени, будут отображаться в строке отчета Сборы .
Просмотреть комиссии за разовый платеж
- Посетите транзакций на своей онлайн-панели Square Dashboard.
- Выберите диапазон дат и примените необходимые фильтры.
- Выберите транзакцию. Плата, уплаченная за транзакцию, будет указана под деталями транзакции.
Бесплатная обработка кредита и возмещение
Когда вы приглашаете друзей присоединиться к Square, вы оба получаете возмещение комиссии за обработку карты.За каждого человека, который активирует свою учетную запись с помощью вашей реферальной ссылки, вы получите возмещение комиссионных за обработку до 1000 долларов США за продажи в течение следующих 180 дней (6 месяцев). После активации ваши друзья также получат бесплатную плату за обработку транзакций до 1000 долларов США.
Узнайте больше о приглашении друзей и отслеживании возмещения расходов с помощью бесплатной программы обработки Square.
Узнайте больше о : Обработка платежей
.Войти
Забыли пароль Инструкции отправлены
Файлы cookie отключены
Этот сайт требует файлов cookie. Пожалуйста, включите файлы cookie в настройках вашего браузера и нажмите кнопку ниже, чтобы продолжить.
Я включил куки
Войти в систему
Проверьте свой почтовый ящик на наличие электронного письма от Square.
Мы только что отправили вам ссылку для завершения входа. Если вы не видите ее в своем почтовом ящике, не забудьте проверить папку со спамом.
Срок действия ссылки для входа истек
Ссылка, которую мы отправили вам для входа, действительна только в течение 5 минут, а теперь срок ее действия истек.Пожалуйста, вернитесь к логину и попробуйте еще раз.
Активировать двухэтапную аутентификацию
Администратор вашей учетной записи требует, чтобы вы настроили двухэтапную аутентификацию. Узнать больше>Выберите метод двухэтапной аутентификации:
Активировать двухэтапную аутентификацию
Администратор вашей учетной записи требует, чтобы вы настроили двухэтапную аутентификацию.Узнать больше>Мы будем отправлять вам текст подтверждения каждый раз, когда вы входите в Личный кабинет или Регистрируетесь.
Мы будем отправлять вам текст подтверждения каждый раз, когда вы входите в Личный кабинет или Регистрируетесь.
Активировать двухэтапную аутентификацию
Администратор вашей учетной записи требует, чтобы вы настроили двухэтапную аутентификацию.Узнать больше> Отсканируйте этот штрих-код с помощью приложения для двухфакторной аутентификации, чтобы начать генерировать безопасные пароли. Узнать больше> Отсканируйте этот штрих-код с помощью приложения для двухфакторной аутентификации, чтобы начать генерировать безопасные пароли. Узнать больше>следующий
Я не могу отсканировать штрих-код
Код ручной настройки
Используйте этот ключевой код, чтобы добавить свою учетную запись Square в приложение аутентификации.Узнать больше>Завершить двухэтапную аутентификацию
Настройка двухэтапной аутентификации завершена
Теперь ваша учетная запись защищена двухэтапной аутентификацией.
Перейти к приборной панели
Введите код подтверждения
Требуется дополнительная проверка
Сброс пароля
Введите адрес электронной почты, который вы использовали для регистрации в Square, и мы пришлем вам инструкции по сбросу пароля.
Сброс пароля
Проверьте свой почтовый ящик на наличие электронного письма от Square.
Мы только что отправили вам обновленную ссылку для сброса пароля. Если вы не видите его в своем почтовом ящике, не забудьте проверить папку со спамом.
Срок действия ссылки для сброса пароля истек
Сброс пароля выполнен успешно
Активация аккаунта
Проверьте свой почтовый ящик на наличие электронного письма от Square.
Мы только что отправили вам обновленную ссылку для активации вашей учетной записи. Если вы не видите его в своем почтовом ящике, не забудьте проверить папку со спамом.
Срок действия ссылки для активации аккаунта истек
Активируйте свою новую учетную запись Square
Активация аккаунта прошла успешно
Активация аккаунта прошла успешно
Аккаунт уже активирован
Срок действия пароля истек
Ваш пароль истек.Вам нужно будет сбросить пароль перед входом в Square. Узнать больше>Сброс пароля
Срок действия вашего пароля истечет
Если вы не обновите свой пароль до истечения его срока, вы не сможете войти в Square.Узнать больше>Сброс пароля
Продолжать
,math — Решение системы линейных уравнений в неквадратной матрице
Переполнение стека- Товары
- Клиенты
- Случаи использования
- Переполнение стека Общественные вопросы и ответы
- Команды Частные вопросы и ответы для вашей команды
- предприятие Частные вопросы и ответы для вашего предприятия
- работы Программирование и связанные с ним возможности технической карьеры
- Талант Нанять технических талантов
Система линейных уравнений — Simple English Wikipedia, бесплатная энциклопедия
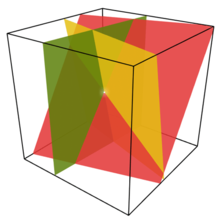 Линейная система с тремя переменными определяет набор плоскостей (по одной плоскости для каждого уравнения). Точка пересечения — это решение.
Линейная система с тремя переменными определяет набор плоскостей (по одной плоскости для каждого уравнения). Точка пересечения — это решение.В математике система линейных уравнений (или линейная система ) представляет собой набор линейных уравнений с одним и тем же набором переменных.
Математики показывают взаимосвязь между различными факторами в форме уравнений.«Линейные уравнения» означают, что переменная появляется только один раз в каждом уравнении без возведения в степень. «Система» линейных уравнений означает, что все уравнения верны одновременно. Итак, человек, решающий систему уравнений, ищет значения каждой переменной, которые сделают все уравнения истинными одновременно. Если никакие такие значения не могут удовлетворить все уравнения в системе, то уравнения называются «несовместимыми».
Например,
- 3 Икс + 2 Y — Z знак равно 1 2 Икс — 2 Y + 4 Z знак равно — 2 — Икс + 1 2 Y — Z знак равно 0 {\ displaystyle {\ begin {alignat} {7} 3x && \; + \; && 2y && \; — \; && z && \; = \; && 1 & \\ 2x && \; — \; && 2y && \; + \; && 4z && \; = \ ; && — 2 & \\ — x && \; + \; && {\ tfrac {1} {2}} y && \; — \; && z && \; = \; && 0 & \ end {alignat}}}
— это система трех уравнений от трех переменных Икс {\ displaystyle x} , Y {\ displaystyle y} , Z {\ displaystyle z} ,«Решение» линейной системы — это присвоение чисел переменным таким образом, чтобы все уравнения выполнялись одновременно. Решение указанной выше системы дается формулой
- Икс знак равно 1 Y знак равно — 2 Z знак равно — 2 {\ displaystyle {\ begin {alignat} {2} x & = & 1 \\ y & = & — 2 \\ z & = & — 2 \ end {alignat}}}
, поскольку при этом выполняются все три уравнения: [1]
- 3 ( 1 ) + 2 ( — 2 ) — ( — 2 ) знак равно 1 2 ( 1 ) — 2 ( — 2 ) + 4 ( — 2 ) знак равно — 2 — ( 1 ) + 1 2 ( — 2 ) — ( — 2 ) знак равно 0 {\ displaystyle {\ begin {alignat} {7} 3 (1) && \; + \; && 2 (-2) && \; — \; && (- 2) && \; = \; && 1 & \\ 2 (1 ) && \; — \; && 2 (-2) && \; + \; && 4 (-2) && \; = \; && — 2 & \\ — (1) && \; + \; && {\ tfrac {1 } {2}} (- 2) && \; — \; && (- 2) && \; = \; && 0 & \ конец {alignedat}}}
В математике теория линейных систем — это раздел линейной алгебры, предмет, который является фундаментальным для современной математики.Компьютерные алгоритмы поиска решений являются важной частью численной линейной алгебры, и такие методы играют важную роль в инженерии, физике, химии, информатике и экономике. Система нелинейных уравнений часто может быть аппроксимирована линейной системой (см. Линеаризация), что является полезным методом при создании математической модели, компьютерной модели или компьютерного моделирования относительно сложной системы. Для сложных систем существует множество уравнений и много переменных, а не только две или три.Во многих случаях количество уравнений и переменных в системе одинаково. В некоторых случаях переменных больше, чем уравнений, и решение будет представлять собой диапазон различных значений, а не одно точное решение.
Простейшая линейная система включает два уравнения и две переменные:
- 2 Икс + 3 Y знак равно 6 4 Икс + 9 Y знак равно 15 ,{\ displaystyle {\ begin {alignat} {5} 2x && \; + \; && 3y && \; = \; && 6 & \\ 4x && \; + \; && 9y && \; = \; && 15 &. \ end {alignat}}}
Один из методов решения такой системы заключается в следующем. Сначала решите верхнее уравнение для Икс {\ displaystyle x} с точки зрения Y {\ displaystyle y} :
- Икс знак равно 3 — 3 2 Y ,{\ displaystyle x = 3 — {\ frac {3} {2}} y.}
Теперь подставьте это выражение для x в нижнее уравнение:
- 4 ( 3 — 3 2 Y ) + 9 Y знак равно 15. {\ displaystyle 4 \ left (3 — {\ frac {3} {2}} y \ right) + 9y = 15.}
Это приводит к единственному уравнению, включающему только переменную Y {\ displaystyle y} , Решение дает Y знак равно 1 {\ displaystyle y = 1} , и подставив это обратно в уравнение для Икс {\ displaystyle x} доходность Икс знак равно 3 / 2 {\ displaystyle x = 3/2} :
- 2 ( 3 2 ) + 3 ( 1 ) знак равно 6 4 ( 3 2 ) + 9 ( 1 ) знак равно 15 ,{\ displaystyle {\ begin {alignat} {5} 2 \ left ({\ frac {3} {2}} \ right) && \; + \; && 3 (1) && \; = \; && 6 & \\ 4 \ left ({\ frac {3} {2}} \ right) && \; + \; && 9 (1) && \; = \; && 15 &. \ end {alignat}}}
Этот метод обобщается на системы с дополнительными переменными.
Очень часто все коэффициенты записываются в виде матрицы A, которая называется матрицей коэффициентов.
- знак равно [ 11 12 ⋯ 1 N 21 22 ⋯ 2 N ⋮ ⋮ ⋱ ⋮ м 1 м 2 ⋯ м N ] {\ displaystyle A = {\ begin {bmatrix} a_ {11} & a_ {12} & \ cdots & a_ {1n} \\ a_ {21} & a_ {22} & \ cdots & a_ {2n} \\\ vdots & \ vdots & \ ddots & \ vdots \\ a_ {m1} & a_ {m2} & \ cdots & a_ {mn} \ end {bmatrix}}}
Примерно так же переменные можно записать в виде вектора:
- Икс знак равно [ Икс 1 Икс 2 ⋮ Икс N ] ; б знак равно [ б 1 б 2 ⋮ б м ] {\ displaystyle x = {\ begin {bmatrix} x_ {1} \\ x_ {2} \\\ vdots \\ x_ {n} \ end {bmatrix}}; \ qquad b = {\ begin {bmatrix} b_ { 1} \\ b_ {2} \\\ vdots \\ b_ {m} \ end {bmatrix}}} ,
Это позволяет писать
- ⋅ Икс знак равно б {\ displaystyle A \ cdot x = b} ,
Математически определенный выше вектор представляет собой матрицу размером 1 на n. Затем система уравнений может быть решена с помощью операции умножения, определенной для матриц. A, x и b — все части одного алгебраического поля.
Решение системы линейных уравнений [изменить | изменить источник]
Возможны три случая поиска решения системы линейных уравнений:
- Нет решения
- Есть ровно одно решение
- Есть много решений; точное количество зависит от свойств поля.Во многих случаях существует бесконечное количество решений.
Есть две категории методов решения системы линейных уравнений. Итерационные методы используют много шагов для получения решения, прямые методы требуют только одного шага:
- Примером прямого метода является решение системы для одной переменной; эту переменную можно исключить и заменить выражением, в котором используются только другие переменные, или числом. Выполнение этого для всех переменных уравнения приведет к решению системы, если оно существует.
- Другой метод — преобразовать два уравнения так, чтобы одна из сторон уравнений была одинаковой в обоих случаях; тогда можно написать другое уравнение, которое заменяет два уравнения и сокращает количество уравнений на одно.
- Исключение по Гауссу
- QR-разложение
- Разложение Холецкого
- Правило Крамера
Примеры итерационных методов:
Есть примеры, такие как геодезия, где измерений намного больше, чем неизвестных.Такая система почти всегда переопределена и не имеет точного решения. Каждое измерение обычно неточно и включает некоторую погрешность. Поскольку измерения неточны, невозможно получить точное решение системы линейных уравнений; такие методы, как наименьшие квадраты, могут использоваться для вычисления решения, которое наилучшим образом соответствует переопределенной системе. Это решение методом наименьших квадратов часто можно использовать как замену точному решению.
Решение системы линейных уравнений имеет сложность не более O (n 3 ).Для решения общей системы из n линейных уравнений требуется не менее n 2 операций. Лучший алгоритм, известный на сегодняшний день, был разработан Доном Копперсмитом и Шмуэлем Виноградом и датируется 1990 годом. Его сложность n 2,376 [2] К сожалению, практического применения он не имеет.
Использование компьютеров для решения систем линейных уравнений используется каждый день. Например, он используется в моделях прогнозирования погоды. Фабрики хот-догов используют его, чтобы внести небольшие изменения в рецепт при изменении цен на пищевые ингредиенты.Кафетерии колледжей используют его, чтобы выяснить, сколько еды нужно приготовить, исходя из прошлого опыта, когда в кафетерии студентам предоставляется выбор между несколькими блюдами.
- ↑ Линейная алгебра, обсуждаемая в этой статье, — это очень хорошо сложившаяся математическая дисциплина, для которой существует множество источников. Почти весь материал в этой статье можно найти в Lay 2005, Meyer 2001 и Strang 2005.
- ↑ Джин Голуб, Чарльз Ван Лоан: Matrix Computations , Johns Hopkins University Press, 3-е издание, 1996; ISBN 978-0-8018-5414-9
Учебники [изменить | изменить источник]
- Axler, Sheldon Jay (1997), Linear Algebra Done Right (2-е изд.), Springer-Verlag, ISBN 0387982590
- Лэй, Дэвид К. (22 августа 2005 г.), Линейная алгебра и ее приложения (3-е изд.), Эддисон Уэсли, ISBN 978-0321287137
- Мейер, Карл Д. (15 февраля 2001 г.), Матричный анализ и прикладная линейная алгебра , Общество промышленной и прикладной математики (SIAM), ISBN 978-0898714548
- Пул, Дэвид (2006), Линейная алгебра: современное введение (2-е изд.), Брукс / Коул, ISBN 0-534-99845-3
- Антон, Ховард (2005), Элементарная линейная алгебра (прикладная версия) (9-е изд.), Wiley International
- Леон, Стивен Дж. (2006), Линейная алгебра с приложениями (7-е изд.), Pearson Prentice Hall
- Стрэнг, Гилберт (2005), Линейная алгебра и ее приложения
