Зависимость скорости от частоты вращения: Глава 7. Вращательное движение. Кинематика и динамика

Глава 7. Вращательное движение. Кинематика и динамика

Как правило, в любом варианте задания ЕГЭ по физике представлены несколько задач на вращательное движение. Приведем основные определения и законы, необходимые для решения такого рода задач. Угловой скоростью тела, совершающего вращательное движение, называется отношение угла поворота к тому времени , за которое этот поворот произошел

(7.1)

В этом определении угол должен измеряться в радианах, поэтому размерность угловой скорости рад/с (или 1/с поскольку радиан — безразмерная величина). В принципе, определение (7.1) позволяет найти как среднюю (для больших интервалов времени ), так и мгновенную (при ) угловую скорость. Однако в школьном курсе физики рассматривается только движение с постоянной угловой скоростью, для которого определение (7.1) дает один и тот же результат для любых интервалов времени . Применяя определение (7. 1) к полному обороту тела (угол поворота — радиан), получим связь угловой скорости и периода вращения

(7.2)

Угловую скорость можно ввести не только для точечного тела, но и для протяженного тела. Действительно, при вращении неточечного тела вокруг любой оси все его точки поворачиваются за одинаковое время на одинаковый угол. Поэтому можно говорить об угловой скорости всего тела.

Из формулы (7.2) легко получить связь угловой и обычной скорости вращающегося точечного тела (в этом контексте последнюю всегда называют линейной скоростью). Умножая правую и левую часть формулы (7.2) на радиус окружности и учитывая, что – это длина пути, пройденного за период, получим

(7.3)

Конечно, для неточечного вращающегося тела нельзя ввести понятие линейной скорости, поскольку у разных точек этого тела линейные скорости будут разными.

Очевидно, при вращательном движении тело всегда имеет ускорение. Действительно, согласно определению (2.1) ускорение тела равно нулю, если не меняется вектор скорости этого тела (т.е. как величина скорости, так и ее направление). При вращательном движении направление скорости обязательно меняется. Можно доказать, что при вращательном движении точечного тела с постоянной по величине линейной скоростью вектор его ускорения в любой момент направлен от тела к центру траектории тела, а его величина равна

(7.4)

Ускорение (7.3) принято называть центростремительным. Если использовать связь линейной и угловой скорости тела при вращательном движении (7.3), то формулу для центростремительного ускорения можно записать и в таких формах

(7.5)

Согласно второму закону Ньютона ускорения сообщаются телам силами. Поэтому если тело совершает движение по окружности радиуса с постоянной по величине скоростью (и соответственно угловой скоростью ), на него должна действовать сила, направленная к центру окружности и равная по величине

(7.6)

Силу (7.6) принято называть центростремительной. Отметим, что термин «центростремительная» связан не с природой этой силы, а с тем, как она действует: в разных ситуациях центростремительной силой может быть и сила тяжести, и сила трения, и сила реакции, и другие силы или их комбинации.

Перечисленных законов и определений достаточно для решения любых задач ЕГЭ на вращательное движение. Рассмотрим их применение к решению задач, приведенных в первой части.

Если период вращения тела задан, то его угловая скорость может быть однозначно определена независимо от размеров тела или радиуса орбиты для точечного тела. В частности, секундная стрелка любых часов поворачивается на угол за одну минуту (конечно, при условии, что они идут «правильно»).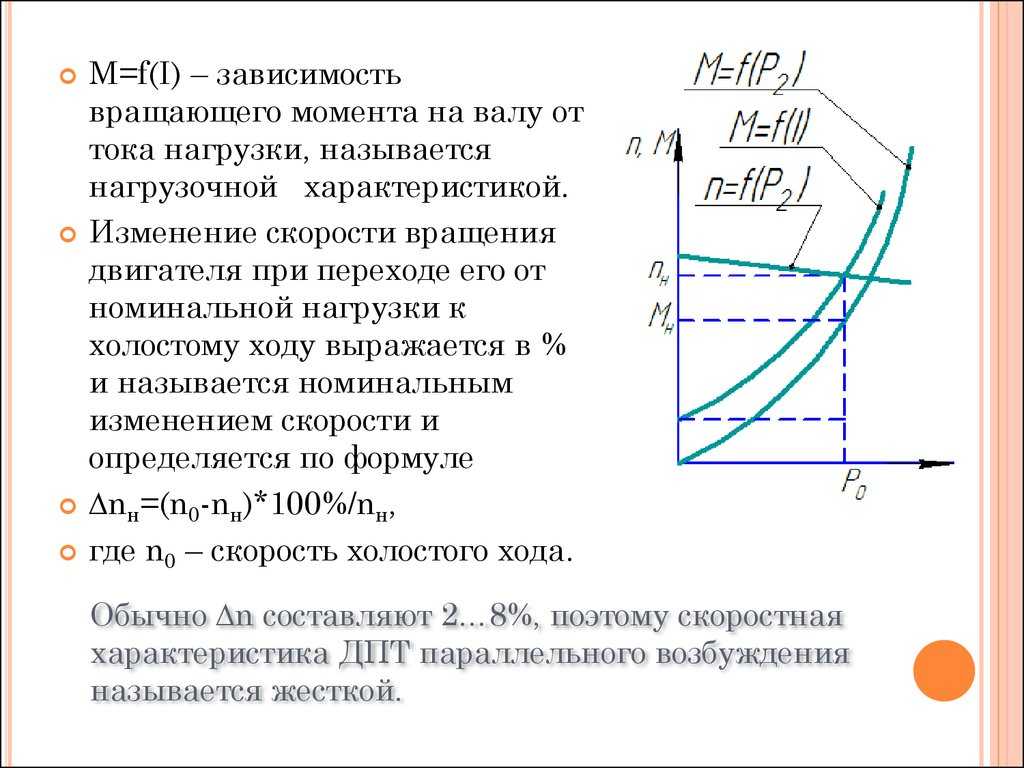 Поэтому угловая скорость секундных стрелок любых часов равна рад/мин (задача 7.1.1 – ответ 2).

Для нахождения линейной скорости конца секундной стрелки часов (задача 7.1.2) используем связь угловой и линейной скоростей (7.5). Имеем

(правильный ответ – 2).

Применяя определение угловой скорости к колесу (задача 7.1.3), получаем

(правильный ответ 1).

Из формулы (7.2) имеем

(задача 7.1.4 – правильный ответ 4).

Используя известное расстояние от первой точки до оси вращения и ее центростремительное ускорение (задача 7.1.5), из формулы (7.5) находим квадрат угловой скорости диска

А теперь по формуле (7. 5) для второй точки получаем

(ответ 2).

Поскольку скорость автомобиля в задаче 7.1.6 не меняется в процессе движения для сравнения центростремительных ускорений автомобиля в разных точках траектории следует использовать формулу (7.4), из которой находим, что ускорение тем больше, чем меньше радиус траектории (правильный ответ –

3).

Ускорение мальчика из задачи 7.1.7 будет равно нулю, если его скорость относительно земли будет равна нулю. Поэтому при движении мальчика против движения карусели, его скорость относительно карусели равна скорости карусели относительно земли . Если мальчик пойдет в другую сторону с той же скоростью относительно карусели, его скорость относительно земли будет равна . Поэтому центростремительное ускорение мальчика будет равно

(ответ 4).

Тело, находящееся на поверхности вращающегося диска и вращающееся вместе с ним (задача 7.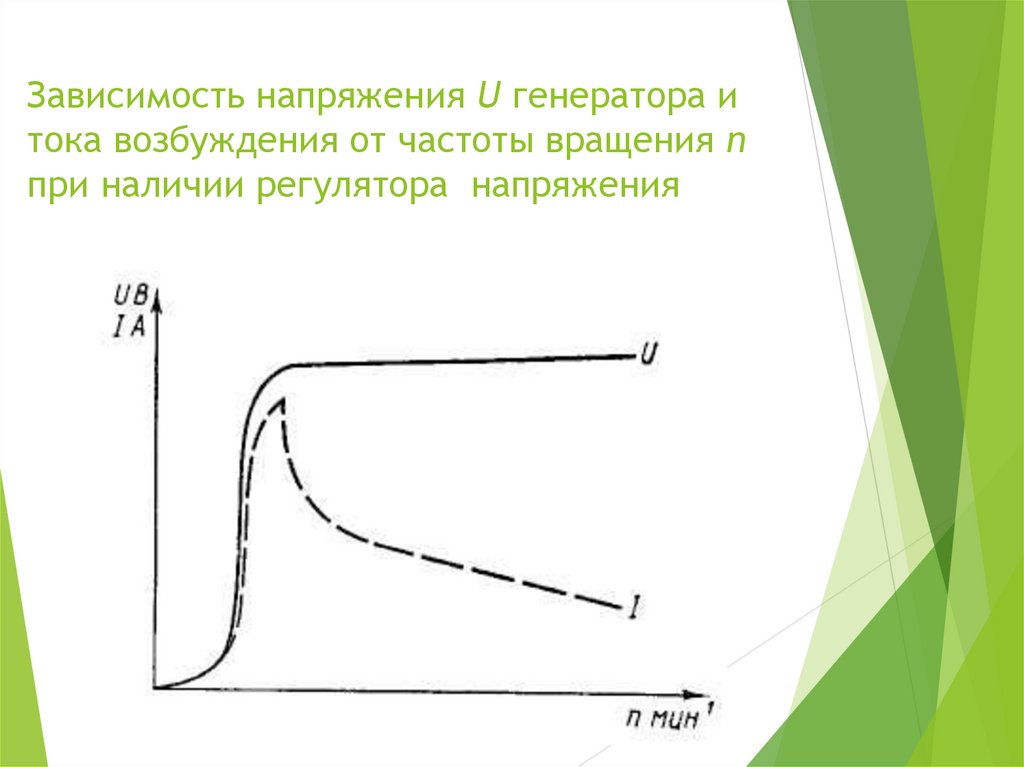 1.8), участвует в следующих взаимодействиях. Во-первых, тело притягивается к земле (сила тяжести), и на него действует поверхность диска (сила нормальной реакции и трения), причем сила трения в каждый момент времени направлена к оси вращения (см. рисунок). Действительно, в отсутствии силы трения тело либо будет оставаться на месте, а диск под ним будет вращаться, либо (если тело имеет скорость) слетит с поверхности диска. Именно сила трения «заставляет» тело вращаться вместе с диском. Поэтому сила трения служит в данной задаче цен-тростремительной силой. Остальные перечисления, данные в условии: «на тело действуют силы тяжести, трения, реакции опоры, центростремительная (или центробежная)» являются неправильными, поскольку в них смешиваются характеристики сил разных типов – первые три касаются природы взаимодействий, вторые – результат действия. Поэтому правильный ответ на вопрос задачи –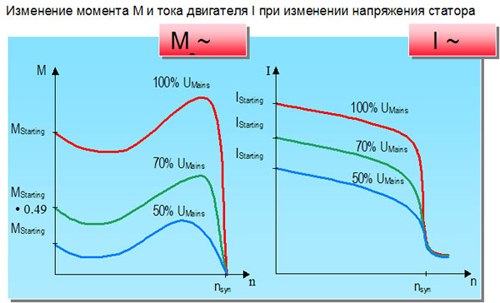

1. Кроме того, отметим, что центробежная сила возникает только в неинерциальных системах отсчета и в школьном курсе физики не рассматривается (поэтому лучше этим понятием вообще не пользоваться).

Поскольку тело в задаче 7.1.9 вращается с постоянной по величине скоростью по окружности, то его ускорение направлено к центру окружности, и, следовательно, согласно второму закону Ньютона, туда же направлена и результирующая сила, действующая на тело (ответ 2).

Применяя к данному в задаче 7.1.10 телу второй закон Ньютона и учитывая, что его ускорение равно м/с², получим для равнодействующей =2 Н (ответ 2).

Используя формулу для центростремительного ускорения , находим отношение ускорений материальных точек из задачи 7.2.1

(ответ 1).

Для сравнения центростремительных ускорений материальных точек в задаче 7.2.2 удобно использовать формулу , поскольку в этой задаче одинаковы угловые скорости точек. Получаем

(ответ 3).

Для сравнения центростремительных ускорений тел в задаче 7. 2.3 выразим ускорение через радиус окружности и период. Используя формулу (7.2) для периода и (7.5) для центростремительного ускорения, получим

(7.5)

Поэтому

(ответ 1).

Используя связь угловой и линейной скорости, находим скорости концов часовой и минутной стрелки (задача 7.2.4)

где и – угловые скорости часовой и минутной стрелки соответственно (в рад/час), и – длины часовой и минутной стрелок. Учитывая, что , получаем

(ответ 2).

Телу, вращающемуся вместе с диском на его горизонтальной поверхности (задача 7.2.5), центростремительное ускорение сообщается силой трения

Поэтому при увеличении угловой скорости вращения диска возрастает и сила трения между телом и диском. При некоторой угловой скорости сила трения достигнет максимально возможного для нее значения . Если еще увеличить угловую скорость диска, сила трения уже не сможет удержать тело на диске: тело начнет скользить по поверхности и слетит с поверхности диска. Поэтому значения угловой скорости, при которой тело может вращаться вместе с диском, находится из неравенства

(ответ 4

).

В задаче 7.2.6 центростремительной силой является сила натяжения нити. Поэтому из второго закона Ньютона с учетом формулы (7.5) для центростремительного ускорения имеем

(ответ 3).

В задаче 7.2.7 нужно использовать второй закон Ньютона для каждого тела. Силы, действующие на тела, показаны на рисунке. Проекция второго закона Ньютона для дальнего тела на координатную ось, направленную к центру диска, дает

(1)

На ближнее тело действуют силы натяжения и двух нитей (см. рисунок). Поэтому для него из второго закона Ньютона имеем

Подставляя в эту формулу силу из формулы (1), находим (ответ 2).

В задаче 7.2.8 необходимо использовать то обстоятельство, что угловая скорость всех точек стержня одинакова. Обозначая расстояния от оси вращения до концов стержня как и , имеем

где = 1 м/с и = 2 м/с – линейные скорости концов стержня, м – его длина. Решая эту систему уравнений, найдем расстояния и , а затем и угловую скорость стержня . В результате получим

(ответ 3).

Среднее ускорение тела за некоторый интервал времени (не обязательно малый) определяется по формуле (2.1):

где и – скорости тела в конце и начале интервала времени . За половину периода вектор скорости поворачивается на 180°, поэтому величина разности равна . Поэтому среднее ускорение тела за половину периода равно

(задача 7.2.9 – ответ 1).

Очевидно, при зубчатой передаче совпадают линейные скорости точек на ободе шестерней. Действительно, если бы эти скорости были разными, между поверхностями шестерней было бы проскальзывание, которому препятствуют зубцы шестерней (задача 7.2.10 – ответ 2).

Угловая скорость: формула частоты вращения

Иногда применительно к автомобилям всплывают вопросы из математики и физики. В частности, одним из таких вопросов является угловая скорость. Она имеет отношение как к работе механизмов, так и к прохождению поворотов. Разберёмся же, как определить эту величину, в чём она измеряется и какими формулами тут нужно пользоваться.

Содержание

• Как определить угловую скорость: что это за величина?
• Формула времени, за которое вращается точка по окружности заданного радиуса
• Угол поворота и период обращения
• Чему равна угловая скорость в конкретных случаях?
• Связь угловой и линейной скоростей
• Ускорение, момент и связь их с массой
• Шарнир как пример передачи импульса

Как определить угловую скорость: что это за величина?

С физико-математической точки зрения эту величину можно определить следующим образом: это данные, которые показывают, как быстро некая точка осуществляет оборот вокруг центра окружности, по которой она движется.

ПОСМОТРЕТЬ ВИДЕО

Эта, казалось бы, чисто теоретическая величина, имеет немалое практическое значение при эксплуатации автомобиля. Вот лишь несколько примеров:

• Необходимо правильно соотносить движения, с которыми вращаются колёса при повороте. Угловая скорость колеса автомобиля, движущегося по внутренней части траектории, должна быть меньше, чем у внешнего.
• Требуется рассчитывать, насколько быстро в автомобиле вращается коленвал.
• Наконец, сама машина, проходя поворот, тоже имеет определённую величину параметров движения – и от них на практике зависит устойчивость автомобиля на трассе и вероятность опрокидывания.

Формула времени, за которое вращается точка по окружности заданного радиуса

Для того, чтобы рассчитывать угловую скорость, используется следующая формула:

ω = ∆φ /∆t

Где:

• ω (читается «омега») – собственно вычисляемая величина.
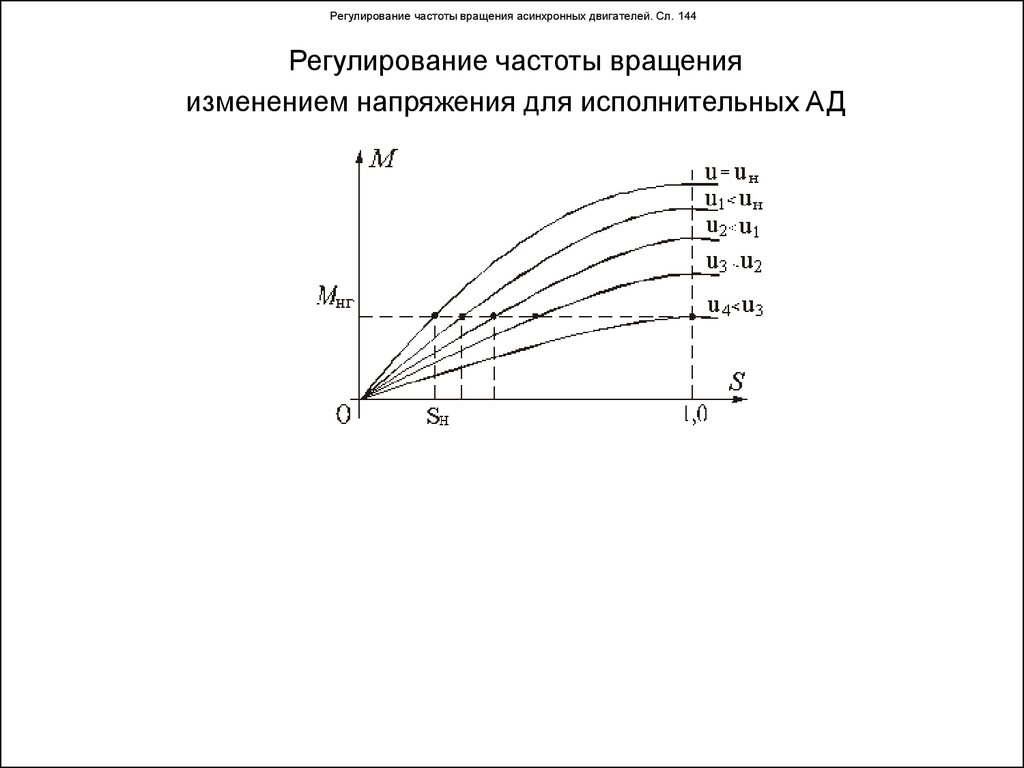
• ∆φ (читается «дельта фи») – угол поворота, разница между угловым положением точки в первый и последний момент времени измерения.
• ∆t
  (читается «дельта тэ») – время, за которое произошло это самое смещение. Точнее, поскольку «дельта», это означает разницу между значениями времени в момент, когда было начато измерение и когда закончено.

Приведённая выше формула угловой скорости применяется лишь в общих случаях. Там же, где речь идёт о равномерно вращающихся объектах или о связи между движением точки на поверхности детали, радиусом и временем поворота, требуется использовать другие соотношения и методы. В частности, тут уже будет необходима формула частоты вращения.

Угловая скорость измеряется в самых разных единицах. В теории часто используется рад/с (радиан в секунду) или градус в секунду. Однако эта величина мало что означает на практике и использоваться может разве что в конструкторской работе. На практике же её больше измеряют в оборотах за секунду (или минуту, если речь идёт о медленных процессах). В этом плане она близка к частоте вращения.

Угол поворота и период обращения

Гораздо более часто, чем угол поворота, используется частота вращения, которая показывает, сколько оборотов делает объект за заданный период времени. Дело в том, что радиан, используемый для расчётов – это угол в окружности, когда длина дуги равна радиусу. Соответственно в целой окружности находится 2 π радианов. Число же π – иррациональное, и его нельзя свести ни к десятичной, ни к простой дроби. Поэтому в том случае, если происходит равномерное вращение, проще считать его в частоте. Она измеряется в об/мин – оборотах в минуту.

Если же дело касается не длительного промежутка времени, а лишь того, за который происходит один оборот, то здесь используется понятие периода обращения. Она показывает, как быстро совершается одно круговое движение. Единицей измерения здесь будет выступать секунда.

Связь угловой скорости и частоты вращения либо периода обращения показывает следующая формулы:

ω = 2 π / T = 2 π *f,

где:

• ω – угловая скорость в рад/с;
• T – период обращения;
• f – частота вращения.

Получить любую из этих трёх величин из другой можно с помощью правила пропорций, не забыв при этом перевести размерности в один формат (в минуты либо секунды)

Чему равна угловая скорость в конкретных случаях?

Приведём пример расчёта на основе приведённых выше формул. Допустим, имеется автомобиль. При движении на 100 км/ч его колесо, как показывает практика, делает в среднем 600 оборотов за минуту (f = 600 об/мин). Рассчитаем угловую скорость.

Для начала переведем об/мин в об/с. Для этого разделим 600 на 60 (число секунд в минуте) и получим 10 об/с . Попутно мы получили и период обращения: эта величина является обратной по отношению к частоте и при измерении в секундах 0,1 с.

Далее используем формулу:

ω = 2 π *f

Поскольку точно выразить π десятичными дробями невозможно, результат примерно равен будет 62,83 рад/с.

Связь угловой и линейной скоростей

На практике часто приходится проверять не только ту скорость, с какой изменяется угловое положение у вращающейся точки, но и скорость её самой применительно к линейному движению. В приведённом выше примере были сделаны расчёты для колеса – но колесо движется по дороге и либо вращается под действием скорости автомобиля, либо само ему эту скорость обеспечивает. Значит, каждая точка на поверхности колеса помимо угловой будет иметь и линейную скорость.

Рассчитать её проще всего через радиус. Поскольку скорость зависит от времени (которым будет период обращения) и пройденного расстояния (которым является длина окружности), то, учитывая приведённые выше формулы, угловая и линейная скорость будут соотноситься так:

V = ωR

Где:

• V – линейная скорость;
• R – радиус.

Из формулы очевидно, что чем больше радиус, тем выше и значение такой скорости. Применительно к колесу с самой большой скоростью будет двигаться точка на внешней поверхности протектора (R максимален), но вот точно в центре ступицы линейная скорость будет равна нулю.

Ускорение, момент и связь их с массой

Помимо приведённых выше величин, с вращением связано ещё несколько моментов. Учитывая же, сколько в автомобиле крутящихся деталей разного веса, их практическое значение нельзя не учесть.

Равномерное вращение – это важная вещь. Вот только нет ни одной детали, которая бы всё время крутилась равномерно. Число оборотов любого крутящегося узла, от коленвала до колеса, всегда в конечном итоге растёт, а затем падает. И та величина, которая показывает, насколько выросли обороты, называется угловым ускорением. Поскольку она производная от угловой скорости, измеряется она в радианах на секунду в квадрате (как линейное ускорение – в метрах на секунду в квадрате).

С движением и её изменением во времени связан и другой аспект – момент импульса. Если до этого момента мы могли рассматривать только чисто математические особенности движения, то здесь уже нужно учитывать то, что каждая деталь имеет массу, которая распределена вокруг оси. Он определяется соотношением начального положения точки с учётом направления движения – и импульса, то есть произведения массы на скорость. Зная момент импульса, возникающий при вращении, можно определить, какая нагрузка будет приходиться на каждую деталь при её взаимодействии с другой

Шарнир как пример передачи импульса

Характерным примером того, как применяются все перечисленные выше данные, является шарнир равных угловых скоростей (ШРУС) . Эта деталь используется прежде всего на переднеприводных автомобилях, где важно не только обеспечить разный темп вращения колёс при повороте – но и при этом их управляемость и передачу на них импульса от работы двигателя.

ПОСМОТРЕТЬ ВИДЕО

Конструкция этого узла как раз и предназначена для того, чтобы:

• уравнивать между собой, как быстро вращаются колёса;
• обеспечивать вращение в момент поворота;
• гарантировать независимость задней подвеске.

В результате все формулы, приведённые выше, учитываются в работе ШРУС.

Скорость против скорости

Как расстояние и перемещение имеют совершенно разные значения (несмотря на их сходство), так и скорость и скорость. Скорость — это скалярная величина, которая относится к тому, «как быстро движется объект». Скорость можно рассматривать как скорость, с которой объект преодолевает расстояние. Быстро движущийся объект имеет высокую скорость и преодолевает относительно большое расстояние за короткий промежуток времени. Сравните это с медленно движущимся объектом с низкой скоростью; он покрывает относительно небольшое расстояние за то же время. Объект без движения имеет нулевую скорость.

 

Скорость как векторная величина

Скорость — это векторная величина, которая относится к «скорости, с которой объект меняет свое положение». Представьте себе человека, который быстро движется — один шаг вперед и один шаг назад — и всегда возвращается в исходное исходное положение. Хотя это может привести к безумной активности, это приведет к нулевой скорости. Поскольку человек всегда возвращается в исходное положение, движение никогда не приведет к изменению положения. Поскольку скорость определяется как скорость изменения положения, это движение приводит к нулевой скорости. Если человек в движении хочет максимизировать свою скорость, то этот человек должен приложить все усилия, чтобы максимизировать величину, на которую он смещается от своего исходного положения. Каждый шаг должен быть направлен на то, чтобы продвинуть этого человека дальше от того, с чего он начал. Наверняка человек ни в коем случае не должен менять направления и начинать возвращаться в исходное положение.

Скорость является векторной величиной. Таким образом, скорость знает направление . При оценке скорости объекта необходимо следить за направлением. Было бы недостаточно сказать, что объект имеет скорость 55 миль в час. Необходимо включить информацию о направлении, чтобы полностью описать скорость объекта. Например, вы должны описать скорость объекта как 55 миль/ч, восток . Это одно из существенных различий между скоростью и скоростью. Скорость является скалярной величиной и не следить за направлением ; скорость является векторной величиной и знает направление .

 

Определение направления вектора скорости

Задача описания направления вектора скорости проста. Направление вектора скорости совпадает с направлением движения объекта. Не имеет значения, ускоряется объект или замедляется. Если объект движется вправо, то его скорость описывается как направленная вправо. Если объект движется вниз, то его скорость описывается как нисходящая. Таким образом, самолет, летящий на запад со скоростью 300 миль/час, имеет скорость 300 миль/час на запад. Обратите внимание, что скорость не имеет направления (это скаляр), а скорость в любой момент времени — это просто значение скорости с направлением.

 

Расчет средней скорости и средней скорости

Когда объект движется, его скорость часто меняется. Например, во время обычной поездки в школу происходит много изменений скорости. Вместо того, чтобы измеритель скорости поддерживал устойчивые показания, стрелка постоянно движется вверх и вниз, отражая остановку и запуск, ускорение и замедление. В один момент машина может двигаться со скоростью 50 миль в час, а в другой момент она может остановиться (т. е. 0 миль в час). Тем не менее, во время поездки в школу человек может проехать в среднем 32 мили в час. Среднюю скорость во время всего движения можно рассматривать как среднее значение всех показаний спидометра. Если бы показания спидометра можно было собирать с интервалом в 1 секунду (или с интервалом в 0,1 секунды, или…), а затем усреднять вместе, можно было бы определить среднюю скорость. Теперь это будет много работы. И, к счастью, есть короткий путь. Читай дальше.

 

Средняя скорость во время движения часто рассчитывается по следующей формуле:

Средняя скорость, напротив, часто рассчитывается по этой формуле

Давайте начнем реализацию нашего понимания этих формул со следующей задачи:

В: Во время отпуска Лиза Карр преодолела в общей сложности 440 миль. Ее поездка заняла 8 часов. Какова была ее средняя скорость?

Чтобы вычислить ее среднюю скорость, мы просто делим пройденное расстояние на время в пути.

Это было просто! Лиза Карр в среднем разгонялась до 55 миль в час. Возможно, она не двигалась с постоянной скоростью 55 миль в час. Она, несомненно, была остановлена ​​в какой-то момент времени (возможно, для перерыва в ванной или на обед), и, вероятно, в другие моменты времени она двигалась со скоростью 65 миль в час. Тем не менее, она развивала среднюю скорость 55 миль в час. Приведенная выше формула представляет собой сокращенный метод определения средней скорости объекта.

Средняя скорость по сравнению с мгновенной скоростью

Поскольку движущийся объект часто меняет свою скорость во время движения, принято различать среднюю скорость и мгновенную скорость. Различие заключается в следующем.

• Мгновенная скорость — скорость в любой данный момент времени.
• Средняя скорость — среднее значение всех мгновенных скоростей; находится просто по соотношению расстояние/время.

Вы можете думать о мгновенной скорости как о скорости, которую показывает спидометр в любой данный момент времени, а о средней скорости как о среднем значении всех показаний спидометра в ходе поездки. Поскольку задача усреднения показаний спидометра была бы достаточно сложной (а может быть, и опасной), среднюю скорость чаще рассчитывают как отношение расстояния к времени.

Движущиеся объекты не всегда движутся с неустойчивой и меняющейся скоростью. Иногда объект будет двигаться с постоянной скоростью с постоянной скоростью. То есть объект будет преодолевать одно и то же расстояние каждый регулярный интервал времени. Например, бегун по пересеченной местности может бежать с постоянной скоростью 6 м/с по прямой в течение нескольких минут. Если ее скорость постоянна, то расстояние, пройденное за каждую секунду, одинаково. Бегун будет преодолевать расстояние 6 метров каждую секунду. Если бы мы могли измерять ее положение (расстояние от произвольной начальной точки) каждую секунду, то мы бы заметили, что положение меняется на 6 метров каждую секунду. Это будет резко контрастировать с объектом, который меняет свою скорость. Объект с изменяющейся скоростью будет перемещаться на разное расстояние каждую секунду. В приведенных ниже таблицах данных изображены объекты с постоянной и изменяющейся скоростью.

Теперь давайте снова рассмотрим движение этого учителя физики. Учитель физики проходит 4 метра на восток, 2 метра на юг, 4 метра на запад и, наконец, 2 метра на север. Все движение длилось 24 секунды. Определить среднюю скорость и среднюю скорость.

Учитель физики прошел 12 метров за 24 секунды; таким образом, ее средняя скорость составила 0,50 м/с. Однако, поскольку ее перемещение равно 0 м, ее средняя скорость равна 0 м/с. Помните, что смещение относится к изменению положения, а скорость зависит от этого изменения положения. В этом случае движения учителя происходит изменение положения на 0 метров и, следовательно, средняя скорость равна 0 м/с.

Вот еще один пример, аналогичный тому, что мы видели ранее при обсуждении расстояния и смещения. На приведенной ниже диаграмме показано положение лыжника в разное время. В каждый из указанных моментов времени лыжник поворачивается и меняет направление движения. Другими словами, лыжник движется от A к B, затем C и D.

Используйте диаграмму, чтобы определить среднюю скорость и среднюю скорость лыжника в течение этих трех минут. Когда закончите, нажмите кнопку, чтобы просмотреть ответ.

В качестве последнего примера рассмотрим футбольного тренера, расхаживающего взад-вперед вдоль боковой линии. На приведенной ниже диаграмме показаны несколько позиций тренера в разное время. В каждой отмеченной позиции тренер делает «разворот» и движется в обратном направлении. Другими словами, тренер перемещается из позиции A в B, затем в C и затем в D.

Какова средняя скорость и средняя скорость тренера? Когда закончите, нажмите кнопку, чтобы просмотреть ответ.

В заключение, скорость и скорость являются кинематическими величинами, которые имеют совершенно разные определения. Скорость, будучи скалярной величиной, представляет собой скорость, с которой объект преодолевает расстояние. Средняя скорость — это расстояние (скалярная величина) за отношение времени. Скорость не знает направления . С другой стороны, скорость — векторная величина; это с учетом направления . Скорость – это скорость изменения положения. Средняя скорость — это смещение или изменение положения (векторная величина) за отношение времени.

 

Мы хотели бы предложить …

Иногда недостаточно просто прочитать об этом. Вы должны взаимодействовать с ним! И это именно то, что вы делаете, когда используете один из интерактивов The Physics Classroom. Мы хотели бы предложить вам совместить чтение этой страницы с использованием нашего интерактива Name That Motion. Он находится в разделе «Интерактивная физика» и позволяет учащемуся применять понятия скорости, скорости и ускорения.

Посетите назовите это движение.

 

Следующий раздел:

Перейти к следующему уроку:

Почему в США не используется метрическая система?

проверено Cite

Несмотря на то, что были приложены все усилия для соблюдения правил стиля цитирования, могут быть некоторые расхождения. Пожалуйста, обратитесь к соответствующему руководству по стилю или другим источникам, если у вас есть какие-либо вопросы.

Выберите стиль цитирования

MLAAPAChicago Руководство по стилю

Написано

Джонатан Хогебак

Стажер редактора Британской энциклопедии.

Джонатан Хогебак

Факт проверен

Редакторы Британской энциклопедии

Редакторы Encyclopaedia Britannica курируют предметные области, в которых они обладают обширными знаниями, будь то многолетний опыт, полученный в результате работы над этим контентом, или в результате обучения для получения ученой степени. Они пишут новый контент, а также проверяют и редактируют контент, полученный от участников.

Редакторы Encyclopaedia Britannica

© serato/Shutterstock.com

Конституция Соединенных Штатов гласит в разделе 8 статьи I, что Конгресс имеет право «устанавливать стандарт мер и весов». Принятие решения о системе, регулирующей то, как США измеряют объекты, сравнивают длину и взвешивают себя, без сомнения, было первоочередной задачей для членов-основателей страны. Когда они начали проверять потенциальные системы примерно в 179 году0, недавно разработанная французская метрическая система привлекла внимание госсекретаря Томаса Джефферсона. Хотя это было так близко, Джефферсон и даже Франция, намного позже, решили пройти, и США приняли Британскую имперскую систему измерения (та, которая до сих пор используется в стране). С тех пор у США было много возможностей перейти на метрическую систему, которая используется в большинстве стран мира и считается более логичной и простой. Так почему же он не изменился?

Основные причины, по которым США не приняли метрическую систему, — это просто время и деньги. Когда в стране началась промышленная революция, дорогие производственные предприятия стали основным источником американских рабочих мест и потребительских товаров. Поскольку в то время действовала Имперская система измерений (IS), оборудование, используемое на этих фабриках, было разработано с учетом размеров в единицах IS; все рабочие прошли обучение работе с подразделениями ИБ; и многие продукты были сделаны с блоками IS. Всякий раз, когда в Конгрессе возникало обсуждение перехода на систему единиц измерения, принятие законопроекта в пользу метрической системы препятствовало крупным предприятиям и американским гражданам, которые не хотели проходить через трудоемкую и дорогостоящую процедуру изменения всей инфраструктуры страны. . Многие также считали, что Соединенные Штаты должны сохранить свою особую систему, отличающую их от других стран и символизирующую их статус лидера, а не последователя.