Ратутилера это: Что такое фанкойл Что такое чиллер – Тейлор, Фредерик Уинслоу — Википедия

Тейлор, Фредерик Уинслоу — Википедия

В Википедии есть статьи о других людях с фамилией Тейлор.

Фредерик Уинслоу Тейлор (или Тэйлор; англ. Frederick Winslow Taylor; 20 марта 1856 (1856-03-20), Филадельфия, Пенсильвания — 21 марта 1915, Филадельфия) — американский инженер, основоположник научной организации труда и менеджмента (см. тейлоризм).

Фредерик Уинслоу Тейлор родился в семье адвоката. Получил образование во Франции и Германии, затем — в академии Филлипса в Эксетере в Нью-Хэмпшире. В 1874 году окончил Гарвардский юридический колледж, но из-за проблем со зрением не смог продолжить образование и устроился работать рабочим пресса в промышленные мастерские заводы гидрооборудования в Филадельфии. В 1878 году, в пик экономической депрессии, получил место разнорабочего на Мидвэльском сталелитейном заводе (англ.).

С 1882 по 1883 году работал начальником механических мастерских. Параллельно получил техническое образование (степень инженера-механика, Технологический институт Стивенса, 1883). В 1884 г. Тейлор стал главным инженером, в этом же году впервые использовал систему дифференциальной оплаты за производительность труда.

С 1890 по 1893 гг. Тейлор — главный управляющий Мануфактурной инвестиционной компании в Филадельфии, владелец бумажных прессов в Мэне и Висконсине, организовал собственное дело по управленческому консультированию, первое в истории менеджмента. В 1906 г. Тейлор становится президентом Американского общества инженеров-механиков, а в 1911 г. — учреждает Общество содействия научному менеджменту.

С 1895 г. Тейлор начал свои всемирно известные исследования по научной организации труда. Оформил патентами около сотни своих изобретений и рационализаций.

Тейлор умер 21 марта 1915 года в Филадельфии от воспаления лёгких.

В США Тейлор в своё время подвергался повсеместным нападкам. Кампания «всеобщего презрения», поднятая профсоюзными боссами того времени против Тейлора, считается одной из самых злобных в американской истории. Согласно Тейлору, любой квалифицированный и неквалифицированный труд мог быть проанализирован, систематизирован и передан в процессе обучения любому человеку. Впоследствии из его идей выросла современная система профессионально-технического обучения. Профсоюзы же тех времен были по преимуществу кастовыми образованиями, где ревниво охраняли свои «секреты мастерства», не систематизировали свои знания и не имели подчас никакого письменного их описания. Идеи Тейлора настолько задевали их интересы, что профсоюзные лидеры добились от Конгресса принятия закона, который запретил «исследования рабочих операций» на государственных оружейных заводах и судоверфях. Эти запреты действовали даже по окончании Второй мировой войны.

Капиталисты также критиковали Тейлора — поскольку он упорно настаивал на том, что львиная доля роста доходов в результате внедрения «научных методов управления» должна доставаться рабочим, а не владельцам предприятий. Тейлор писал в своих работах: «Главнейшей задачей управления предприятием должно быть обеспечение максимальной прибыли для предпринимателя в соединении с максимальным благосостоянием для каждого занятого в предприятии работника».

Также Тейлор полагал, что власть на предприятиях не должна принадлежать его владельцу только на основании права собственности. Управлять должны специально подготовленные люди, которые в нынешней терминологии называются менеджерами. Для капиталистов того времени это было чудовищной ересью. В печати его называли «социалистом» и «смутьяном».

На предприятиях Америки того времени, последовательно внедривших научные методы Тейлора, не было зафиксировано ни одного случая стачки рабочих или иных социальных конфликтов, несмотря на трудности, с которыми там столкнулись при внедрении новшеств. При всех недостатках его теории дух партнёрства предпринимателя и рабочего, провозглашённый Тейлором, стал основой гуманизации труда. В последующих теориях менеджмента центральным фактором производительного управления стал фактор человеческий. «Не будет стран богатых и бедных — будут страны образованные и невежественные», — писал Тейлор, подразумевая под источником знаний, прежде всего, менеджмент.

Считается, что Дарвин, Маркс и Фрейд преобразовали современный мир. Питер Друкер, признанный гуру менеджмента, утверждал, что Маркса в этом ряду было бы справедливо заменить на Тейлора.

Ленин назвал систему Тейлора «„научной“ системой выжимания пота» (Полн. собр. соч., 5 изд., т. 23, с. 18), системой порабощения человека машиной (см. там же, т. 24, с. 369), которая «…соединяет в себе утонченное зверство буржуазной эксплуатации и ряд богатейших научных завоеваний в деле анализа механических движений при труде, изгнания лишних и неловких движений, выработки правильнейших приёмов работы, введения наилучших систем учёта и контроля и т. д.» (там же, т. 36, с. 189—90). В то же время Ленин рекомендовал выявить содержащиеся в системе Тейлора рациональные элементы и творчески их использовать в Советской России, соединить их «…с сокращением рабочего времени, с использованием новых приёмов производства и организации труда без всякого вреда для рабочей силы трудящегося населения» (там же, с. 141).

• В антиутопии Евгения Замятина «Мы», действие которой происходит в далёком будущем, Ф. У. Тейлор считается самым великим человеком древности. Он затмил по популярности своего однофамильца Б. Тейлора, так как все люди (нумера) Единого Государства приписывают ему все труды последнего.
• «Тейлор был американским инженером и ярким, неуравновешенным человеком. К моменту своей смерти в 1915 году он завоевал репутацию главного „врага рабочих“, после того как в 1911-м его пригласили отстоять свою систему управления перед комитетом Палаты представителей США. Будучи одним из самых критикуемых организационных теоретиков, он оказался также и одним из самых влиятельных. Его принципы научного менеджмента стали краеугольным камнем организации труда в первой половине XX века, а во многих ситуациях превалируют по сей день».
  // Морган, Гэрет Образы организации. М., 2008. — С.42.

• Генри Форд — американский промышленник, владелец заводов по производству автомобилей, одним из первых применивший положения теории Тейлора на практике.

• «Принципы научного управления» (The Principles of Scientific Management), F. W. Taylor, Harper & Brothers, New York, 1911 г.;
• Motion and Time Study: Design and Measurement of Work, edition, R. M. Barnes, John Wiley & Sons, New York, 1968;
• Executive Decisions and Operations Research, D. W. Miller, M. K. Starr, Prentice-Hall, Englewood Cliffs, 1969;
• Work Study, J. A. Larkin, McGraw-Hill, New York, 1969;
• A Computer Perspective, G. Fleck, editor, Harvard University Press, Cambridge, 1973;
• Webster’s New Biographical Dictionary, Merriam-Webster, Springfield, 1988;
• The One Best Way: Frederick Winslow Taylor and the Enigma of Efficiency, R. Kanigel, Viking, New York, 1997

Тейлоризм — Википедия

Материал из Википедии — свободной энциклопедии

Фредерик Тейлор, 1856—1915

Тейлори́зм (англ. Taylorism) — одна из теорий управления или научная организация труда, проанализировавшая и обобщившая рабочие процессы. Её основной целью было повышение экономической эффективности, особенно производительности труда. Использование данного подхода было одной из первых попыток применить науку для конструирования процессов и управления. Основоположник теории — Фредерик Уинслоу Тейлор.

Разработку основ своих теорий Фредерик У. Тейлор начал в 1880-х — 1890-х годах: работая токарем и мастером в обрабатывающей промышленности в компании Midvale Steel, Тейлор заметил естественные различия в производительности рабочих, которые, по его мнению, были вызваны разными причинами, в том числе способностью, уровнем развития интеллекта и мотивации. Тейлор одним из первых попытался теоретизировать происходящее. То есть выявить, какие различия существовали и почему, как это можно объяснить с точки зрения передового опыта, и как это может быть распространено на другие отрасли через пошаговую стандартизацию процессов. Он считал, что принятие решений, основанное на традиции и эмпирических правилах, должно быть заменено точными процедурами, разработанными в ходе тщательного изучения каждого работника, в том числе через исследование времени и движений, которое направлено на выявление или разработку «лучшего способа» выполнения любой задачи

[1]. Цели и назначение состояли в увеличении производительности и снижении затрат.

Впервые Тейлор опубликовал свои теории в монографиях «Управление мастерской» в 1903 г. (англ. Shop Management)^[2][3] и «Принципы научного управления» (англ. The Principles of Scientific Management) в 1911.

Пик влияния тейлоризма пришелся на 1910-е годы.

В 1920-х годах, хотя основы тейлоризма по-прежнему использовались, начиналась эпоха конкуренции и синкретизма с противоположными или более широкими идеями.

К 1930-м годам тейлоризм вообще устарел как отдельная теория или школа мысли. Но большинство тем тейлоризма по-прежнему считаются важной частью промышленной инженерии и менеджмента:

1. Создание научного фундамента для замены старых принципов работы.
2. Отбор работников должен проводиться на научной основе, и в дальнейшем должно реализовываться их профессиональное обучение.
3. Организация стимулирования труда на основе полученного конечного продукта.
4. Сотрудничество работников с администрацией.
5. Справедливое распределение обязанностей между работниками.

Принцип работы чиллеров | Как работает чиллер

Чиллер – это агрегат, предназначенный для охлаждения жидкости, которая используется в качестве теплоносителя систем кондиционирования. На сегодняшний день, самым распространенным видом таких агрегатов являются парокомпрессионные холодильные машины. Схема такого чиллера всегда включает в себя такие основные элементы, как компрессор, испаритель, конденсатор и расширительное устройство.

Принцип работы такой системы построен на поглощении и выделении тепловой энергии за счет изменения агрегатного состояния хладагента в зависимости от воздействующего на него давления. Наиболее важным элементом, от которого в первую очередь зависит работа чиллера, является компрессор, которых на сегодняшний день существует несколько типов:

• роторные;
• спиральные;
• винтовые;
• поршневые;
• центробежные;

Главная задача компрессора заключается в том, чтобы сжимать пары хладагента, тем самым повышая давление, что необходимо для начала конденсации. Далее, горячая парожидкостная смесь попадает в конденсатор (чаще всего воздушного охлаждения), который передает тепловую энергию во внешнюю среду. После того, как хладагент полностью переходит в жидкое состояние, он попадает на расширительное устройство (дроссель), которое расположено перед испарителем и понижает давление до такой степени, чтобы он начал вскипать. Проходя через испаритель, кипящий хладагент полностью переходит в газообразное состояние и поглощает тепловую энергию из теплоносителя, тем самым снижая его температуру.

Приведенная выше схема работы чиллера не изменяется в зависимости от его конструктивного исполнения, которых существует несколько вариантов:

• моноблочные наружной установки;
• моноблочные с центробежными вентиляторами;
• с выносным конденсатором;
• с конденсатором, охлаждаемым жидкостью.

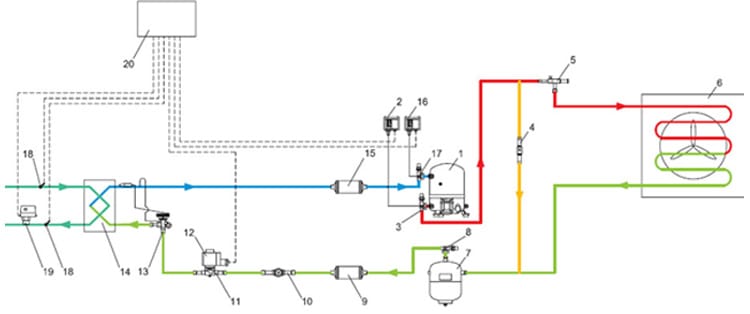
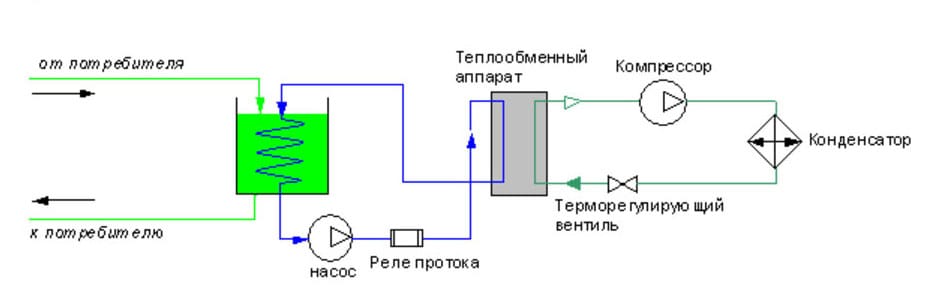
Рисунок 1. Принципиальная схема чиллера с конденсатором воздушного охлаждения. 1- компрессор, 2-реле высокого давления, 3-клапан запорный, 4-клапан дифференциальный, 5-регулятор давления конденсации, 6-конденсатор воздушного охлаждения, 7-ресивер линейный, 8-клапан запорный, 9-фильтр-осушитель, 10-стекло смотровое, 11-клапан соленоидный, 12-катушка для клапана соленоидного, 13-вентиль терморегулирующий, 14-испаритель пластинчатый паяный, 15-фильтр-осушитель, 16-реле низкого давления, 17-клапан запорный, 18-датчик температуры, 19-реле протока жидкости, 20-щит электрический.

Какое бы исполнение вы ни выбрали, принцип работы чиллера всегда остается неизменным. Основополагающим моментом в проектировании оборудования такого типа, является соблюдение рекомендаций изготовителя к установке, в которых четко обозначены необходимый расход теплоносителя (охлаждаемой жидкости), допустимая наружная температура и количество тепловой энергии, которую необходимо отводить.

Виды схем установок охлаждения жидкости (чиллеры)

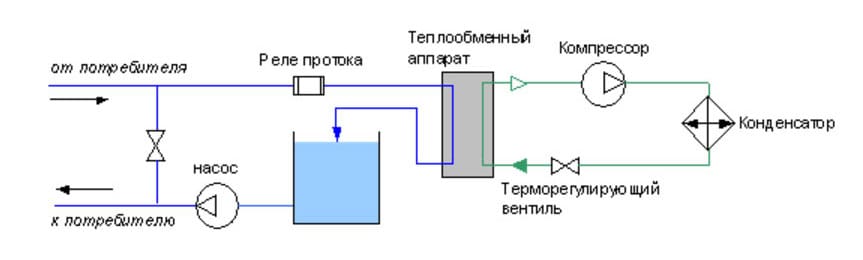
1. Схема непосредственного охлаждения жидкости.

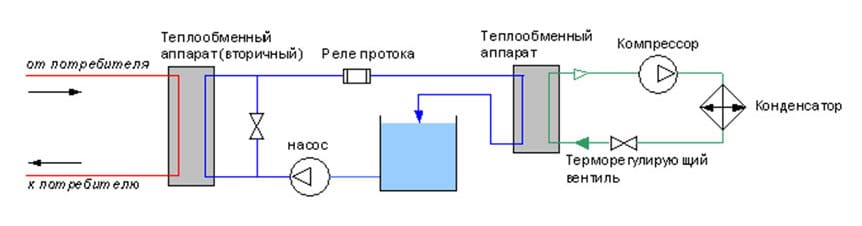
2. Схема охлаждения жидкости с использованием промежуточного хладоносителя и вторичного теплообменного аппарата.

3. Схема охлаждения жидкости с использованием ёмкости-накопителя

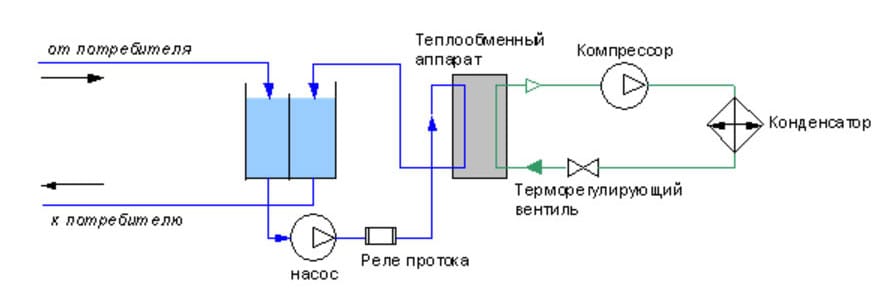
4. Схема охлаждения жидкости с использованием промежуточного хладоносителя и открытого вторичного теплообменного аппарата.

 

Для того чтобы правильно подобрать чиллер, всегда следует обращаться к специалистам, которые хорошо представляют себе, какую именно конструктивную схему предложить для каждого конкретного случая, ведь несмотря на общий принцип работы, каждый элемент установки играет очень важную роль в функциональности системы в целом.

Самая красивая теорема математики: тождество Эйлера / Habr

Посмотрев лекцию профессора Робина Уилсона о тождестве Эйлера, я наконец смог понять, почему тождество Эйлера является самым красивым уравнением. Чтобы поделиться моим восхищением это темой и укрепить собственные знания, я изложу заметки, сделанные во время лекции. А здесь вы можете купить его прекрасную книгу.

Что может быть более загадочным, чем взаимодействие мнимых чисел с вещественными, в результате дающее ничто? Такой вопрос задал читатель журнала Physics World в 2004 году, чтобы подчеркнуть красоту уравнения Эйлера «e в степени i, умноженного на пи равно минус единице».

Рисунок 1.0: тождество Эйлера — e в степени i, умноженного на пи, плюс единица равно нулю.

Ещё раньше, в 1988 году, математик Дэвид Уэллс, писавший статьи для американского математического журнала The Mathematical Intelligencer, составил список из 24 теорем математики и провёл опрос, попросив читателей своей статьи выбрать самую красивую теорему. И после того, как с большим отрывом в нём выиграло уравнение Эйлера, оно получило званием «самого красивого уравнения в математике».

Рисунок 2.0: обложка журнала The Mathematical Intelligencer
Рисунок 3.0: опрос Дэвида Уэллса из журнала

Леонарда Эйлера называют самым продуктивным математиком за всю историю. Других выдающихся математиков вдохновляли его работы. Один из лучших физиков в мире, Ричард Фейнман, в своих знаменитых лекциях по физике назвал уравнение Эйлера «самой примечательной формулой в математике». Ещё один потрясающий математик, Майкл Атья, назвал эту формулу «…математическим аналогом фразы Гамлета — «быть или не быть» — очень короткой, очень сжатой, и в то же время очень глубокой».

Существует множество интересных фактов об уравнении Эйлера. Например, оно встречалось в некоторых эпизодах «Симпсонов».

Рисунок 4.0: в этой сцене уравнение Эйлера можно заметить на второй книге в самой правой стопке.
Рисунок 5.0: в этой сцене уравнение Эйлера написано на футболке второстепенного персонажа.

Также уравнение Эйлера стало ключевым пунктом в уголовном деле. В 2003 году аспирант Калифорнийского технологического института Билли Коттрелл писал краской на чужих спортивных автомобилях уравнение Эйлера. На суде он сказал: «Я знал теорему Эйлера с пяти лет, и её обязаны знать все«.

Рисунок 6.0: марка, выпущенная в 1983 году в Германии в память о двухсотлетии со смерти Эйлера.
Рисунок 7.0: марка, выпущенная Швейцарией в 1957 году в честь 250-й годовщины Эйлера.

Почему уравнение Эйлера так важно?

Вы имеете полное право задаться вопросом: почему Билли Коттрелл считал, что об уравнении Эйлера обязаны знать все? И был настолько в этом уверен, что начал писать его на чужих машинах? Ответ прост: Эйлер воспользовался тремя фундаментальными константами математики и применил математические операции умножения и возведения в степень, чтобы записать красивую формулу, дающую в результате ноль или минус один.

• Константа e связана со степенными функциями.
• Константа i является не вещественным, а мнимым числом, равным квадратному корню из минус единицы.
• Знаменитая константа π (пи) связана с окружностями.

Впервые тождество Эйлера появилось в 1748 году в его книге Introductio in analysin infinitorum. Позже другие люди увидели, что эта формула связана с тригонометрическими функциями синуса и косинуса, и эта связь удивительна, ведь степенная функция стремится к бесконечности, а тригонометрические функции колеблются в интервале от — 1 до -1.

e в степени i, умноженного на ϕ (фи) = cos ϕ + i * sin ϕ

Рисунок 8.0: экспоненциальная функция y=e^x.
Рисунок 8.1: график тождества Эйлера.
Рисунок 8.2: частоты, испускаемые LC-цепью.

Показанные выше уравнения и графы могут показаться абстрактными, но они важны для квантовой физики и вычислений обработки изображений, и при этом зависят от тождества Эйлера.

1: число для счёта

Число 1 (единица) является основой нашей системы исчисления. С неё мы начинаем счёт. Но как мы считаем? Чтобы считать, мы используем цифры 0–9 и систему разрядов, определяющую значение цифры.

Например, число 323 означает 3 сотни, 2 десятка и 3 единицы. Здесь число 3 исполняет две разные роли, которые зависят от его расположения.

323 = (3*100) + (2*10) + (3*1)

Существует и другая система исчисления, называемая двоичной. В этой системе вместо 10 используется основание 2. Она широко применяется в компьютерах и программировании. Например, в двоичной системе:

1001 = (2³) + (0²) + (0¹) + (2⁰) = [9 в системе с основанием 10]

Кто создал системы исчисления? Как первые люди считали предметы или животных?

Как возникли наши системы исчисления? Как считали первые цивилизации? Мы точно знаем, что они не пользовались нашей разрядной системой. Например 4000 лет назад древние египтяне использовали систему исчисления с разными символами. Однако они комбинировали символы, создавая новый символ, обозначающий числа.

Рисунок 11: показанные здесь иероглифы образуют число 4622; это одно из чисел, вырезанных на стене в храме в Карнаке (Египет).
Рисунок 12: иероглифы — это изображения, обозначающие слова, а в данном случае — числа.

В то же время, но в другом месте ещё один социум обнаружил способ подсчёта, но в нём тоже использовались символы. Кроме того, основанием их системы исчисления было 60, а не 10. Мы используем их метод счёта для определения времени; поэтому в минуте 60 секунд, а в часе 60 минут.

Рисунок 13: вавилонские числа из шестидесятиричной системы счисления (с основанием 60).

Тысячу лет спустя древние римляне изобрели римские числа. Для обозначения чисел они использовали буквы. Римская нотация не считается разрядной системой, потому что для многих значений нашей системы счисления в ней использовались разные буквы. Именно по этой причине для счёта они использовали абакус.

Рисунок 14: романский абакус в шестнадцатеричной (с основанием 16) системе счисления
Рисунок 15: таблица преобразования из арабских в римские числа

Древние греки тоже не использовали разрядную систему счисления. Греческие математики обозначали числа буквами. У них были специальные буквы для чисел от 100 до 900. Многие люди в то время считали греческие числа запутанными.

Рисунок 15: таблица букв древних греков.

В то же самое время китайские математики начали использовать для расчётов небольшие бамбуковые палочки. Этот китайский способ счёта называют первой десятичной разрядной системой.

Рисунок 16: китайский способ счёта с числами-палочками. Использовался как минимум с 400 года до нашей эры. Квадратная счётная доска использовалась примерно до 1500 года, когда её заменил абакус.

Однако самая уникальная система счёта использовалась индейцами майя. Их система счисления имела основание 20. Для обозначения чисел от 1 до 19 они использовали точки и линии. Чем же отличалась их система счисления? Для каждого числа они использовали изображения голов и отдельный символ нуля 0.

Рисунок 17: Система счисления майя с основанием 20, в которой числа обозначались головами
Рисунок 18: ещё один способ записи чисел майя.

0: число для обозначения ничего

Некоторые цивилизации использовали пробелы, чтобы, например, отличать число 101 от 11. Спустя какое-то время начало появляться особое число — ноль. К примеру, в пещере в индийском городе Гвалиор археологи обнаружили на стене число 270, в котором был ноль. Самое первое зафиксированное использование нуля можно увидеть в Бодлианской библиотеке.
Рисунок 19: вырезанный на стене храма в Гвалиоре круг обозначает ноль. Ему примерно 1500 лет.
Рисунок 20: чёрные точки в манускрипте Бакхшали обозначают нули; это самый старый письменный пример использования числа, ему примерно 1800 лет.

Примерно 1400 лет назад были записаны правила вычислений с нулём. Например, при сложении отрицательного числа и нуля получается то же отрицательное число. Деление на нуль не допускается, потому что если разделить на ноль, то мы получим число, которое может быть равно любому нужному нам числу, что должно быть запрещено.

Вскоре после этого многими людьми были опубликованы книги по арифметике, распространяющие использование индо-арабской записи чисел. Ниже показана эволюция индо-арабских чисел. В большинстве стран используется индо-арабская система чисел, но арабские страны до сих пор пользуются арабскими числами.

Рисунок 21: на этой схеме показана эволюция чисел, происходящих от чисел брахми и заканчивающаяся числами, которыми мы используем и сегодня.
Рисунок 22: классическая гравюра «Арифметика» из Margarita Philosophica Грегора Рейша, на которой изображено соревнование между Боэцием, улыбающимся после открытия индо-арабских чисел и письменных вычислений, и нахмуренным Пифагором, до сих пор пытающимся пользоваться счётной доской.

Пи (π): самое известное иррациональное число

Пи — самое популярное из известных нам иррациональных чисел. Пи можно найти двумя способами: вычислив соотношение длины окружности к её диаметру, или соотношение площади круга к квадрату его радиуса. Евклид доказал, что эти соотношения постоянны для всех окружностей, даже для луны, пенни, шины и т.д.

π = окружность / диаметр ИЛИ π = площадь круга / радиус²

Рисунок 22: анимированная связь между окружностью и диаметром в отношении пи.

Так как иррациональные числа наподобие пи бесконечны и не имеют повторений, мы никогда не закончим записывать пи. Оно продолжается вечно. Есть люди, запомнившие множество десятичных разрядов пи (нынешний рекорд — 70 000 цифр! Источник: «Книга рекордов Гиннесса» ).

Рисунок 23: данные опроса 941 респондентов для определения процента людей, способных запомнить знаки пи после запятой.
Рисунок 24: На стене станции метро Karlsplatz в Вене записаны сотни разрядов пи.

На данный момент компьютеры смогли вычислить всего 2,7 триллиона разрядов пи. Может казаться, что это много, но на самом деле этот путь бесконечен.

Как я сказал выше, число пи нашёл Евклид. Но как поступали люди до Евклида, когда им нужно было найти площадь круга? Историки обнаружили вавилонскую глиняную табличку, в которой было записано отношение периметра шестиугольника к диаметру описанной вокруг него окружности. После вычислений полученное число оказалось равным 3.125. Это очень близко к пи.

Рисунок 24: вавилонская глиняная табличка с отношением периметра шестиугольника к длине описанной окружности.
Рисунок 25: Numberwarrior

Древние египтяне тоже близко подобрались к значению пи. Историки обнаружили документ, показывающий, как древние египтяне нашли число пи. Когда историки перевели документ, то нашли такую задачу:

Например, чтобы найти площадь поля диаметром 9 хета (1 хет = 52,35 метра), нужно выполнить следующее вычисление:

Вычесть 1/9 диаметра, а именно 1. Остаток равен 8. Умножить его на 8, что даёт нам 64. Следовательно, площадь будет равна 64 setjat (единица измерения площади).

Другими словами, диаметр равен 2r, а 1/9 радиуса равно (1/9 • 2r). Тогда если мы вычтем это из исходного диаметра, то получим 2r — (1/9 • 2r) = 8/9(2r). Тогда площадь круга равна 256/81 r². То есть пи равно почти 3,16. Они обнаружили это значение пи примерно 4000 лет назад.

Рисунок 26: математический папирус Ахмеса.

Однако греческие математики нашли для вычисления пи способ получше. Например, Архимед предпочитал работать с периметрами. Он начал рисовать окружности, описывающие многоугольники разного размера. Когда он чертил шестиугольник, то рисовал окружность с диаметром 1. Затем он видел что каждая сторона шестиугольника равна 1/2, а периметр шестиугольника равен 1/2 x 6 = 3. Затем он увеличивал количество сторон многоугольника, пока он не становился похожим на круг. Работая со 96-сторонним многоугольником и применив тот же способ, он получил 2 десятичных разряда пи после запятой: 3 и 10/71 = 3,14084. Спустя много лет китайский математик Лю Ху использовал 3072-сторонний многоугольник и получил число 3,14159 (5 верных десятичных разрядов числа пи после запятой). После этого ещё один китайский математик Цзу Чунчжи провёл ещё более впечатляющую работу. Он работал со 24000-сторонним многоугольником и получил 3,1415926 — семь верных десятичных разрядов пи после запятой.

Спустя тысячу лет немецкий математик Людольф Цейлен работал со 2⁶²-сторонним многоугольником и получил 35 десятичных разрядов пи. Это число, названное Людольфовым, было высечено на его могильном камне.

В 1706 году англичанин Джон Мэчин, долгое время работавший профессором астрономии, использовал формулу сложения, чтобы доказать, что пи равно
Не беспокоясь о том, как откуда взялась эта формула, Мэчин начал постоянно ею пользоваться, а затем записал показанный ниже ряд. Это был самый большой на то время шаг в количестве разрядов пи.
Рисунок 29: Формула Мэчина для пи

Однако первое упоминание пи появилось в 1706 году. Преподаватель математики Уильям Джонс написал книгу и впервые предложил пи для измерения окружностей. Так пи впервые появилась в книгах!

Рисунок 30: Juliabloggers

В 1873 году Уильям Шэнкс воспользовался формулой Джона Мэчина и получил 707 десятичных разрядов пи. Эти цифры написаны в комнате пи парижского Дворца открытий. Однако позже математики выяснили, что верными являются только 527 разрядов.

Рисунок 31: комната пи

С другой стороны, более интересный способ нахождения пи обнаружил Буффон. Его эксперимент основывался на случайном разбрасывании иголок для оценки пи. Он нарисовал на доске несколько параллельных линий на расстоянии D и взял иголки длиной L. Затем он случайным образом начал бросать иголки на доску и записывал долю иголок, пересекавших линию.

Рисунок 32.0: Science Friday

А после этого другой математик по имени Ладзарини подбросил иголку 3408 раз и получил шесть десятичных разрядов пи с соотношением 355/113. Однако если бы одна иголка не пересекла линию, он получил бы только 2 разряда пи.

Рисунок 32.1: бросание 1000 иголок для оценки приблизительного значения пи

e: история экспоненциального роста

e — это ещё одно знаменитое иррациональное число. Дробная часть e тоже бесконечна, как и у пи. Мы используем число e для вычисления степенного (экспоненциального) роста. Другими словами, мы используем e, когда видим очень быстрый рост или уменьшение.

Один из величайших, а возможно и лучший математик Леонард Эйлер открыл число e в 1736 году и впервые упомянул это особое число в своей книге Mechanica.

Рисунок 33: источник

Чтобы разобраться в экспоненциальном росте, мы можем использовать историю об изобретателе шахмат. Когда он придумал эту игру, то показал её властителю Севера. Царю понравилась игра и он пообещал, что отдаст автору любую награду. Тогда изобретатель попросил нечто очень простое: 2⁰ зерна на первую клетку шахматной доски, 2¹ зерна на вторую клетку доски, 2² зерна — на третью, и так далее. Каждый раз количество зерна удваивалось. Царь Севера подумал, что просьбу будет выполнить легко, но он ошибался, потому то на последнюю клетку нужно было бы положить 2⁶³ зёрен, что равно 9 223 372 036 854 775 808. Это и есть экспоненциальный рост. Он начался с 1, постоянно удваивался, и через 64 шага вырос в огромное число!

Если бы изобретатель шахмат выбрал линейное уравнение, например 2n, то получил бы 2, 4, 6, 8, … 128… Следовательно, в дальней перспективе экспоненциальный рост часто намного превышает полиномиальный.

Кстати, 9 223 372 036 854 775 808–1 — это максимальное значение 64-битного целого числа со знаком.

Рисунок 34: источник: Wikipedia

Число e открыл Эйлер. Однако Якоб Бернулли тоже работал с числом e, когда вычислял сложный процент, чтобы заработать больше денег. Если вложить 100 долларов под 10% дохода, то как будет расти эта сумма? Во-первых, это зависит от того, как часто банк рассчитывает проценты. Например, если он рассчитывает один раз, то мы получим в конце года 110 долларов. Если мы передумаем и будем брать проценты каждые 6 месяцев, то в этом случае мы получим больше 110 долларов. Дело в ттом, что процент, полученный за первые 6 месяцев, тоже получит свой процент. Общая сумма будет равна 110,25 долларов. Можно догадаться, что мы можем получить больше денег, если будем забирать деньги каждый квартал года. А если мы будем делать временной интервал всё короче, то окончательные суммы будут продолжать расти. Такой бесконечный сложный процент сделает нас богатыми! Однако наш общий доход стремится к ограниченному значению, связанному с e.

Бернулли не называл число 2,71828 именем e. Когда Эйлер работал с 2,71828, он возвёл экспоненциальную функцию e в степень x. Свои открытия он изложил в книге The Analysis of Infinite.

В 1798 году Томас Мальтус использовал экспоненциальную функцию в своём эссе, посвящённом пищевому дефициту будущего. Он создал линейный график, показывающий производство пищи и экспоненциальный график, показывающий население мира. Мальтус сделал вывод, что в дальней перспективе экспоненциальный рост победит, и мир ждёт серьёзный дефицит пищи. Это явление назвали «мальтузианской катастрофой». Ньютон тоже использовал эту модель, чтобы показать, как охлаждается чашка чая.

Рисунок 35: закон Ньютона-Рихмана
Рисунок 36: мальтузианская катастрофа

Мнимость числа: i, квадратный корень -1

Долгое время для решения своих задач математикам было достаточно обычных чисел. Однако в какой-то момент для дальнейшего развития им потребовалось открыть нечто новое и загадочное. Например, итальянский математик Кардано пытался разделить число 10 на 2 части, произведение которых было бы равно 40. Чтобы решить эту задачу, он записал уравнение: x (10-x) = 40. Когда он решил это квадратное уравнение, то получил два решения: 5 плюс √-15 и 5 минус √-15, что в то время не имело никакого смысла. Этот результат был бессмысленным, потому что по определению квадратного корня ему нужно было найти число, квадрат которого был бы отрицательным. Однако и положительное, и отрицательное числа в квадрате имеют положительное значение. Как бы то ни было, он нашёл своё уникальное число. Однако первым математиком, назвавшим √-1 (квадратный корень из минус единицы) мнимым числом i, был Эйлер.

Лейбниц дал такой комментарий о мнимом числе √-1:

Комплексные числа — это прекрасное и чудесное убежище божественного духа, почти что амфибия бытия с небытием.

Мы можем складывать, вычитать, умножать и делить мнимые числа. Сложение, вычитание и умножение просты, а деление немного сложнее. Вещественные и мнимые части складываются по отдельности. В случае умножения i² будет равно -1.

После Эйлера математик Каспар Вессель представил мнимые числа геометрически с создал комплексную плоскость. Сегодня мы представляем каждое комплексное число a + bi как точку с координатами (a,b).

Рисунки 37 и 38: комплексные числа

В викторианскую эпоху многие относились к мнимым числам с подозрением. Однако ирландский математик и астроном Уильям Роуэн Гамильтон покончил с этими сомнениями, определив комплексные числа применительно к кватернионам.

Самое красивое уравнение: тождество Эйлера

Тождество Эйлера связывает экспоненциальную функцию с функциями синуса и косинуса, значения которых колеблются от минус единицы до единицы. Чтобы найти связь с тригонометрическими функциями, мы можем представить их в виде бесконечного ряда, истинного для всех значений

Рисунок 39: открытие тождества Эйлера

Рисунок 40: тождество Эйлера

Эйлер никогда не записывал это тождество в явном виде, и мы не знаем, кто впервые записал его. Тем не менее, мы связываем его с именем Эйлера в знак почтения перед этим великим первопроходцем математики.

Фредерик Тейлор. Основоположник научной организации труда и менеджмента

Главная цель любого коммерческого предприятия – улучшение собственных параметров эффективности. Для того чтобы сделать это, нужно увеличить продуктивность работников и сократить ненужные затраты. Фредерик Уинслоу Тейлор выделил факторы, которые влияют на производительность труда, а также выступил создателем системы научного менеджмента. С помощью серии экспериментов он определил средние временные нормы завершения отдельных операций и оптимальных способов их исполнения.

Фредерик Тейлор: биография

Будущий основатель научного менеджмента родился в 1856 году в семье юриста в Пенсильвании. Он учился во Франции и Германии, а затем в Нью-Хэмпшире, в академии Экстера. Первоначально Фредерик Уинслоу Тейлор намеревался стать юристом, как и его отец. Он успешно окончил в 1847 году Гарвардский колледж по этой специальности, но у него обнаружились проблемы со зрением, которые не позволили ему продолжить образование.

Свою карьеру Фредерик Тейлор начал в качестве ученика модельщика, некоторое время был машинистом, но уже в возрасте 35 лет получил должность консультанта по менеджменту после того, как успешно провел серию экспериментов на сталелитейном заводе в Мидвэле, и на основе их результатов внес ценные предложения руководству. Здесь он за шесть лет прошел путь от простого наемного рабочего до главного инженера, параллельно получив заочное техническое образование, и впервые дифференцировал размер зарплаты своих сотрудников в зависимости от их производительности труда.

Профессиональные достижения

В 1890 будущий основоположник тейлоризма заканчивает свою инженерную карьеру и становится главным управляющим в Филадельфийской мануфактурной инвестиционной компании. Но уже через три года он решил начать свой собственный бизнес и стал первым в истории менеджмента частным консультантом. Параллельно Фредерик Тейлор занимался популяризацией научных методов управления производством с помощью своего членства в Американском обществе инженеров-механиков, пока не основал организацию, посвященную исключительно этому вопросу.

Теоретические концепции, которые принесли ему мировую популярность, ученый изложил в трех основных работах:

• «Управление фабрикой»;
• «Принципы научного управления»;
• «Показания перед специальной комиссией Конгресса».

Практическое экспериментирование

Во время работы на сталелитейном предприятии Тейлор занимался исследованием затрат времени на исполнение отдельных производственных операций. Первый эксперимент заключался в измерении ключевых моментов подрезки чугунных чушек. Фредерику Тейлору удалось вывести средние нормы производительности труда, которые потом стали распространяться на всех рабочих. В результате зарплата на предприятии возросла в 1,6 раза за счет увеличения производительности труда почти в 4 раза и рационализации процесса изготовления чушек.

Суть второго эксперимента, проведенного Тейлором, состояла в определении оптимальных способов размещения заготовок на станках с помощью линейки, которая была специально изобретена им самим, и правильных скоростей их разрезания. На предприятии были проведены десятки тысяч опытов, которые позволили выявить 12 факторов, влияющих на конечную эффективность.

Исследовательские теории

Научный менеджмент – это обобщающий термин для тех идей, которые выдвинул Тейлор относительно теорий и практик управления. Его метод предполагает короткие повторяющиеся циклы, подробную последовательность заданий для каждого сотрудника, контроль за выполнением поставленных целей и мотивирование работников с помощью системы материальных вознаграждений. Применяемая сегодня в большинстве организаций дифференцированная система оплаты труда и бонусы за результативность построены именно на его наработках. По мнению главных исследователей организационного менеджмента Анжея Хучински и Дэвида Бьюкенена, эффективность, предсказуемость и контроль за производственным процессом – это главные цели, которые приписывает Фредерик Тейлор своему научному методу управления.

Связь личной и профессиональной жизни

Поскольку в результате рассмотренных практических наработок сокращался спрос на труд, озлобленные рабочие даже пытались убить ученого. Первоначально против него выступали даже крупные предприниматели, а в Конгрессе США была создана специальная комиссия для изучения его выводов.

С 1895 года Тейлор полностью посвятил себя исследованию научной организации труда. Со временем он пришел к выводу, что благосостояние предприятия возможно только при наличии благоприятных условий для каждого работника. Ученый умер в возрасте 59 лет от воспаления легких, оставив после себя выводы, которые вдохновляют исследователей и предпринимателей и сегодня.

Фредерик Тейлор: принципы менеджмента

Научная система управления базируется на трех «китах»: нормирование трудовых процессов, систематический отбор и повышение квалификации персонала, денежная мотивация как вознаграждение за высокую производительность. Главная причина неэффективности по Тейлору – это несовершенство стимулов для поощрения работников, поэтому именно им должен уделять внимание современный предприниматель.

В основе разработанной ученым системы организации труда лежат 4 принципа:

• Пристальное внимание к отдельным составляющим производственного процесса для установления законов и формул их эффективного исполнения.
• Тщательный отбор сотрудников, их обучение и повышение квалификации, а также увольнение тех, которые оказываются не способными понять научные методы управления.
• Обратная связь руководства с работниками и сближение производства и науки.
• Распределение функций между сотрудниками и менеджментом: первые отвечают за качество и количество конечного продукта, другие – за выработку рекомендаций по совершенствованию организации труда.

Вышеперечисленные принципы Тейлора доказали свою правильность, ведь спустя век они лежат в основе функционирования любого предприятия, а изучение построения системы управления — это одно из главных направлений исследования.

почему один раз увидеть лучше, чем сто раз услышать

Если вы думаете, что ничего не знаете о кругах Эйлера, вы ошибаетесь. На самом деле вы наверняка не раз с ними сталкивались, просто не знали, как это называется. Где именно? Схемы в виде кругов Эйлера легли в основу многих популярных интернет-мемов (растиражированных в сети изображений на определенную тему).

Давайте вместе разберемся, что же это за круги, почему они так называются и почему ими так удобно пользоваться для решения многих задач.

Происхождение термина

Круги Эйлера – это геометрическая схема, которая помогает находить и/или делать более наглядными логические связи между явлениями и понятиями. А также помогает изобразить отношения между каким-либо множеством и его частью.

Пока не очень понятно, верно? Посмотрите на этот рисунок:

На рисунке представлено множество – все возможные игрушки. Некоторые из игрушек являются конструкторами – они выделены в отдельный овал. Это часть большого множества «игрушки» и одновременно отдельное множество (ведь конструктором может быть и «Лего», и примитивные конструкторы из кубиков для малышей). Какая-то часть большого множества «игрушки» может быть заводными игрушками. Они не конструкторы, поэтому мы рисуем для них отдельный овал. Желтый овал «заводной автомобиль» относится одновременно к множеству «игрушки» и является частью меньшего множества «заводная игрушка». Поэтому и изображается внутри обоих овалов сразу.

Ну что, так стало понятнее? Именно поэтому круги Эйлера – это тот метод, который наглядно демонстрирует: лучше один раз увидеть, чем сто раз услышать. Его заслуга в том, что наглядность упрощает рассуждения и помогает быстрее и проще получить ответ.

Автор метода — ученый Леонард Эйлер (1707-1783). Он так и говорил о названных его именем схемах: «круги подходят для того, чтобы облегчить наши размышления». Эйлер считается немецким, швейцарским и даже российским математиком, механиком и физиком. Дело в том, что он много лет проработал в Петербургской академии наук и внес существенный вклад в развитие российской науки.

До него подобным принципом при построении своих умозаключений руководствовался немецкий математик и философ Готфрид Лейбниц.

Метод Эйлера получил заслуженное признание и популярность. И после него немало ученых использовали его в своей работе, а также видоизменяли на свой лад. Например, чешский математик Бернард Больцано использовал тот же метод, но с прямоугольными схемами.

Свою лепту внес также немецкий математике Эрнест Шредер. Но главные заслуги принадлежат англичанину Джону Венну. Он был специалистом в логике и издал книгу «Символическая логика», в которой подробно изложил свой вариант метода (использовал преимущественно изображения пересечений множеств).

Благодаря вкладу Венна метод даже называют диаграммами Венна или еще Эйлера-Венна.

Зачем нужны круги Эйлера?

Круги Эйлера имеют прикладное назначение, то есть с их помощью на практике решаются задачи на объединение или пересечение множеств в математике, логике, менеджменте и не только.

Если говорить о видах кругов Эйлера, то можно разделить их на те, что описывают объединение каких-то понятий (например, соотношение рода и вида) – мы их рассмотрели на примере в начале статьи.

А также на те, что описывают пересечение множеств по какому-то признаку. Таким принципом руководствовался Джон Венн в своих схемах. И именно он лежит в основе многих популярных в интернете мемов. Вот вам один из примеров таких кругов Эйлера:

Забавно, правда? И главное, все сразу становится понятно. Можно потратить много слов, объясняя свою точку зрения, а можно просто нарисовать простую схему, которая сразу расставит все по местам.

Кстати, если вы не можете определиться, какую профессию выбрать, попробуйте нарисовать схему в виде кругов Эйлера. Возможно, чертеж вроде этого поможет вам определиться с выбором:

Те варианты, которые окажутся на пересечении всех трех кругов, и есть профессия, которая не только сможет вас прокормить, но и будет вам нравиться.

Решение задач с помощью кругов Эйлера

Давайте рассмотрим несколько примеров задач, которые можно решить с помощью кругов Эйлера.

Вот на этом сайте — http://logika.vobrazovanie.ru/index.php?link=kr_e.html Елена Сергеевна Саженина предлагает интересные и несложные задачи, для решения которых потребуется метод Эйлера. Используя логику и математику, разберем одну из них.

Задача про любимые мультфильмы

Шестиклассники заполняли анкету с вопросами об их любимых мультфильмах. Оказалось, что большинству из них нравятся «Белоснежка и семь гномов», «Губка Боб Квадратные Штаны» и «Волк и теленок». В классе 38 учеников. «Белоснежка и семь гномов» нравится 21 ученику. Причем трем среди них нравятся еще и «Волк и теленок», шестерым — «Губка Боб Квадратные Штаны», а один ребенок одинаково любит все три мультфильма. У «Волка и теленка» 13 фанатов, пятеро из которых назвали в анкете два мультфильма. Надо определить, скольким же шестиклассникам нравится «Губка Боб Квадратные Штаны».

Решение:

Так как по условиям задачи у нас даны три множества, чертим три круга. А так как по ответам ребят выходит, что множества пересекаются друг с другом, чертеж будет выглядеть так:

Мы помним, что по условиям задачи среди фанатов мультфильма «Волк и теленок» пятеро ребят выбрали два мультфильма сразу:

Выходит, что:

21 – 3 – 6 – 1 = 11 – ребят выбрали только «Белоснежку и семь гномов».

13 – 3 – 1 – 2 = 7 – ребят смотрят только «Волк и теленок».

Осталось только разобраться, сколько шестиклассников двум другим вариантам предпочитает мультфильм «Губка Боб Квадратные Штаны». От всего количества учеников отнимаем всех тех, кто любит два других мультфильма или выбрал несколько вариантов:

38 – (11 + 3 + 1 + 6 + 2 + 7) = 8 – человек смотрят только «Губка Боб Квадратные Штаны».

Теперь смело можем сложить все полученные цифры и выяснить, что:

мультфильм «Губка Боб Квадратные Штаны» выбрали 8 + 2 + 1 + 6 = 17 человек. Это и есть ответ на поставленный в задаче вопрос.

А еще давайте рассмотрим задачу, которая в 2011 году была вынесена на демонстрационный тест ЕГЭ по информатике и ИКТ (источник — http://eileracrugi.narod.ru/index/0-6).

Условия задачи:

В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» — символ «&».

В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети интернет.

Запрос	Найдено страниц (в тысячах)
Крейсер | Линкор	7000
Крейсер	4800
Линкор	4500

Какое количество страниц (в тысячах) будет найдено по запросу Крейсер & Линкор?

Считается, что все вопросы выполняются практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.

Решение:

При помощи кругов Эйлера изобразим условия задачи. При этом цифры 1, 2 и 3 используем, чтобы обозначить полученные в итоге области.

Опираясь на условия задачи, составим уравнения:

1. Крейсер | Линкор: 1 + 2 + 3 = 7000
2. Крейсер: 1 + 2 = 4800
3. Линкор: 2 + 3 = 4500

Чтобы найти Крейсер & Линкор (обозначенный на чертеже как область 2), подставим уравнение (2) в уравнение (1) и выясним, что:

4800 + 3 = 7000, откуда получаем 3 = 2200.

Теперь этот результат мы можем подставить в уравнение (3) и выяснить, что:

2 + 2200 = 4500, откуда 2 = 2300.

Ответ: 2300 — количество страниц, найденных по запросу Крейсер & Линкор.

Как видите, круги Эйлера помогают быстро и просто решить даже достаточно сложные или просто запутанные на первый взгляд задачи.

Заключение

Полагаю, нам удалось убедить вас, что круги Эйлера – не просто занимательная и интересная штука, но и весьма полезный метод решения задач. Причем не только абстрактных задач на школьный уроках, но и вполне себе житейских проблем. Выбора будущей профессии, например.

Вам еще наверняка будет любопытно узнать, что в современной массовой культуре круги Эйлера нашли отражение не только в виде мемов, но и в популярных сериалах. Таких, как «Теория большого взрыва» и «4исла».

Используйте это полезный и наглядный метод для решения задач. И обязательно расскажите о нем друзьям и одноклассникам. Для этого под статьей есть специальные кнопки.

© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.

Диаграмма Эйлера — Википедия

Материал из Википедии — свободной энциклопедии

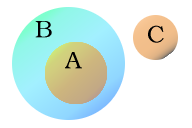Пример кругов Эйлера. Буквами обозначены, например, свойства: B{\displaystyle B} — живое существо, A{\displaystyle A} — человек, C{\displaystyle C} — неживая вещь

Диагра́ммы Э́йлера (круги́ Э́йлера) — геометрическая схема, с помощью которой можно изобразить отношения между подмножествами, для наглядного представления. Первое их использование приписывают Леонарду Эйлеру^[⇨]. Используется в математике, логике, менеджменте и других прикладных направлениях. Не следует их путать с диаграммами Эйлера — Венна^[⇨].

Диаграммы Эйлера также называют кругами Эйлера. При этом «круги» — это условный термин, вместо кругов могут быть любые фигуры.

На диаграммах Эйлера множества изображаются кругами (или другими фигурами). Причём непересекающиеся множества изображены непересекающимися кругами, а подмножества изображены вложенными кругами. Например, диаграмма на рисунке показывает, что множество A является подмножеством B, а B не пересекается с C.

При решении целого ряда задач Леонард Эйлер использовал идею изображения множеств с помощью кругов. Однако этим методом ещё до Эйлера пользовался выдающийся немецкий философ и математик Готфрид Вильгельм Лейбниц. Лейбниц использовал их для геометрической интерпретации логических связей между понятиями, но при этом всё же предпочитал использовать линейные схемы.^[1]

Но достаточно основательно развил этот метод сам Л. Эйлер. Методом кругов Эйлера пользовался и немецкий математик Эрнст Шрёдер в книге «Алгебра логики». Особенного расцвета графические методы достигли в сочинениях английского логика Джона Венна, подробно изложившего их в книге «Символическая логика», изданной в Лондоне в 1881 году. Венн предложил свою схему изображения отношения между множествами, которая теперь называется диаграммами Эйлера — Венна. Первоначально круги Эйлера возникли на основе идей силлогистики Аристотеля. Диаграммы Венна были созданы для решения задач математической логики. Их основная идея разложения на конституенты возникла на основе алгебры логики^[2].

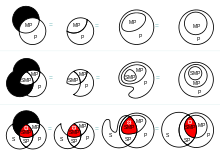Пример получения произвольных кругов Эйлера из диаграмм Венна с пустыми (чёрными) множествами 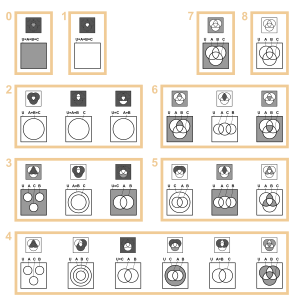22 (из 256) существенно различных диаграмм Венна с 3 кругами (сверху) и соответствующие им диаграммы Эйлера (снизу)

Диаграммы Эйлера — Венна в отличие от диаграмм Эйлера изображают все 2n{\displaystyle 2^{n}} комбинаций n{\displaystyle n} свойств, то есть конечную булеву алгебру. При n=3{\displaystyle n=3} диаграмма Эйлера — Венна обычно изображается в виде трёх кругов с центрами в вершинах равностороннего треугольника и одинаковым радиусом, приблизительно равным длине стороны треугольника.

На рис. ниже даны диаграммы Венна и Эйлера для 3 множеств однозначных натуральных чисел:

• A={1,2,5}{\displaystyle A=\{1,\,2,\,5\}}
• B={1,6}{\displaystyle B=\{1,\,6\}}
• C={4,7}{\displaystyle C=\{4,\,7\}}

• 

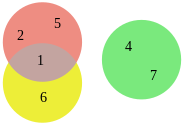
  диаграмма Эйлера

• 

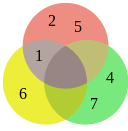
  диаграмма Венна

Иногда, если какая-то комбинация свойств соответствует пустому множеству, то эту комбинацию закрашивают. На рисунке справа даны 22 существенно различных диаграмм Венна с 3 кругами (сверху) и соответствующие им диаграммы Эйлера (снизу). Некоторые из диаграмм Эйлера не типичны, а некоторые даже эквивалентны диаграммам Венна. Черные области указывают на то, что в них нет элементов (пустые множества).

На рисунке внизу дана Диаграмма Эйлера, иллюстрирующая тот факт, что множество существ с 4 конечностями является подмножеством животных, которое не пересекается с множеством минералов.

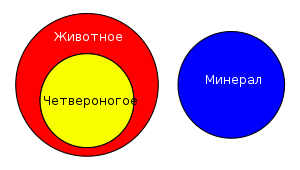Диаграмма Эйлера

1. ↑ Leibniz G. W. Opuscules et fragments inédits de Leibniz. — Paris, 1903. — p. 293—321.
2. ↑ Кузичев, 1968, с. 25.

• Кузичев А. С. Диаграммы Венна. История и применения. — М.: Наука, 1968. — 249 с.

Формальная
Математическая (теоретическая, символическая)	Высказывание — построение над множеством {B,¬,∧,∨,0,1}{\displaystyle \{B,\neg ,\land ,\lor ,0,1\}} 2 константы 0 1
См. также